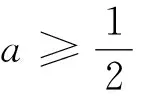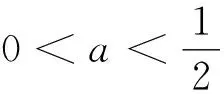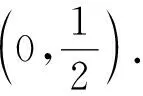稳中求变 变中出新 新中见能 甄别素养
——2023年高考数学全国乙卷评析
陈靖逸 王 勇
湖北省襄阳市第一中学 (441000)
2023年高考数学全国乙卷试题注重基础,强化学科素养,考查关键能力,突出对创新应用能力的考查.试题关注社会发展,引导考生运用所学数学知识解决生活实际问题,富有时代气息,体现了“稳中求变、变中出新、新中见能”的命题理念.试题以数学基础知识、基本技能、基本思想方法为支撑点和立足点,注重对数学通性通法的考查.文、理科试卷针对考生群体的不同数学水平,精心设计,合理布局,准确区分考生.试题加强教考衔接,服务“双减”政策落实,助力基础教育提质增效.试题有利于科学选择人才,有利于深化课程改革,有利于促进社会公平,对培养考生的创新精神、实践能力,提升考生核心素养有积极的导向作用.
一、对选择题的评析
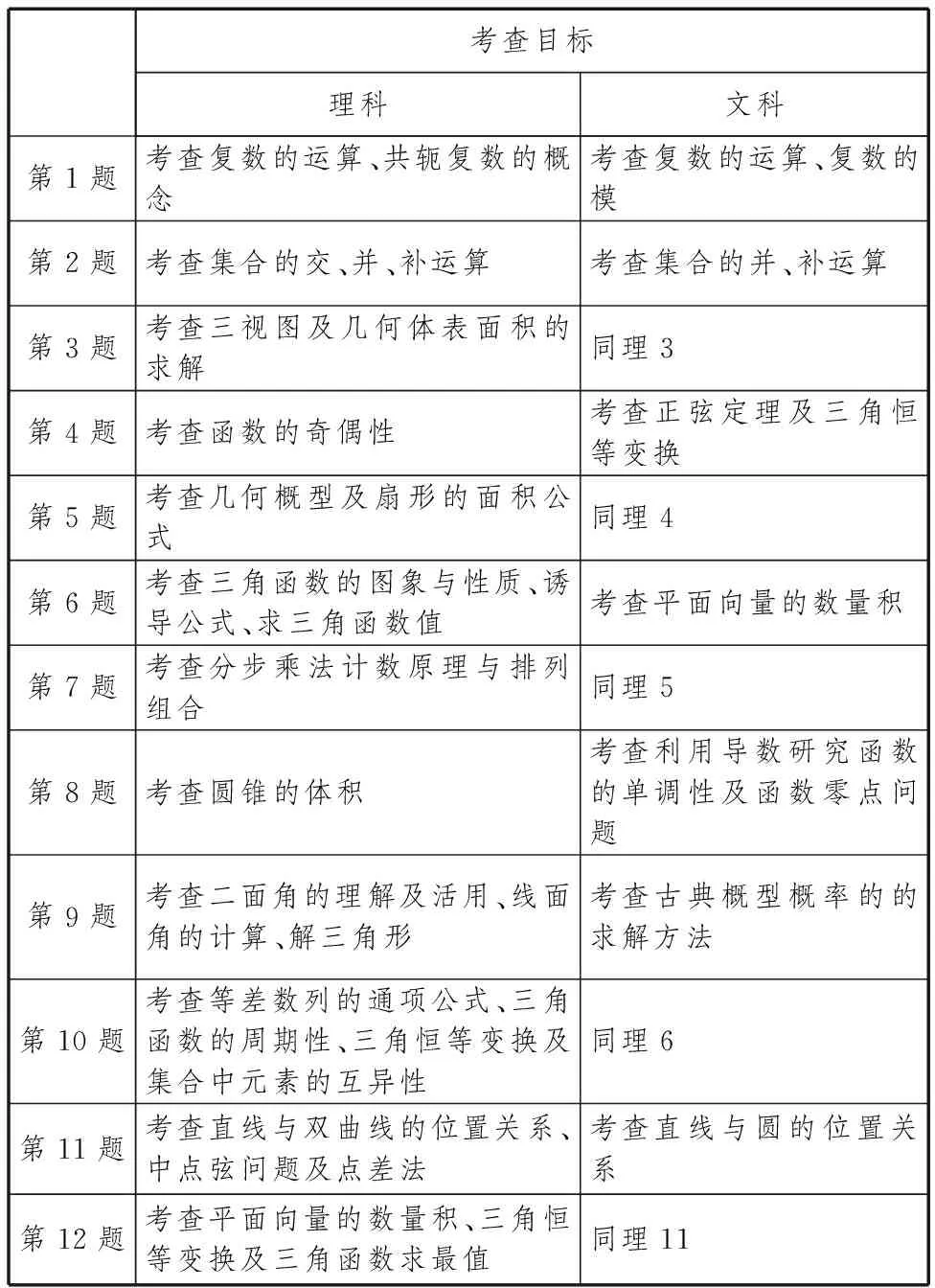
考查目标理科文科第1题考查复数的运算、共轭复数的概念考查复数的运算、复数的模第2题考查集合的交、并、补运算考查集合的并、补运算第3题考查三视图及几何体表面积的求解同理3第4题考查函数的奇偶性考查正弦定理及三角恒等变换第5题考查几何概型及扇形的面积公式同理4第6题考查三角函数的图象与性质、诱导公式、求三角函数值考查平面向量的数量积第7题考查分步乘法计数原理与排列组合同理5第8题考查圆锥的体积考查利用导数研究函数的单调性及函数零点问题第9题考查二面角的理解及活用、线面角的计算、解三角形考查古典概型概率的的求解方法第10题考查等差数列的通项公式、三角函数的周期性、三角恒等变换及集合中元素的互异性同理6第11题考查直线与双曲线的位置关系、中点弦问题及点差法考查直线与圆的位置关系第12题考查平面向量的数量积、三角恒等变换及三角函数求最值同理11
其中理科第10题、理科第11题(文科第12题)、理科第12题颇有研讨价值,下面分别解析,供研读.
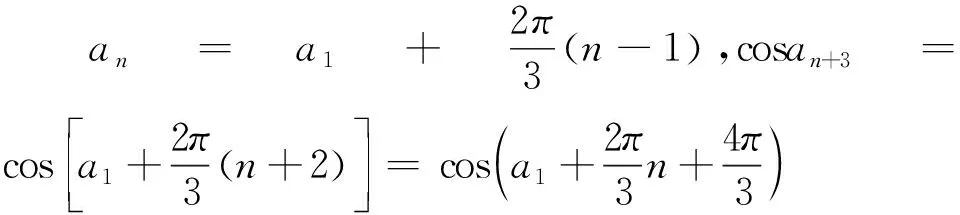
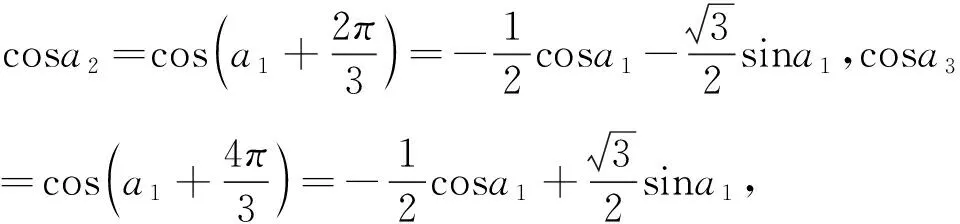
②当cosa1=cosa3≠cosa2时,有cosa1=
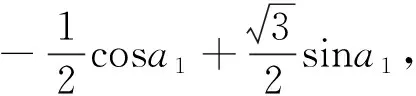
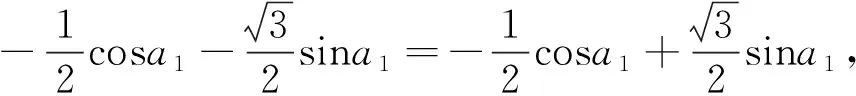
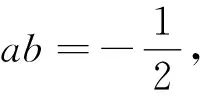
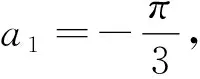
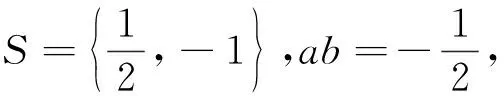
点评:本题将数列、三角函数、集合等知识结合起来,设问简洁,角度新颖,考查知识全面,着重考查考生的理性思维和数学探索等学科素养,考查分类讨论思想,要求考生灵活应用所学知识解决综合性问题,有较强的选拔作用.
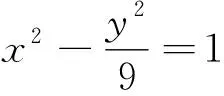
A.(1,1) B.(-1,2) C.(1,3) D.(-1,-4)
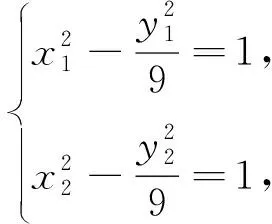
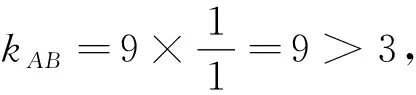
点评:本题将中点弦问题和直线与双曲线的位置关系有机整合,设问角度新颖,重点考查数形结合思想和逻辑推理能力,考生需将问题转化为判断直线AB与双曲线是否有两个交点,逐一验证选项是否正确,考查考生灵活运用所学知识解决综合问题的能力,在注重考查基础知识的同时,对考生的思维能力要求较高,具有较好的选拔功能.
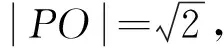
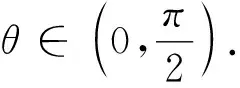
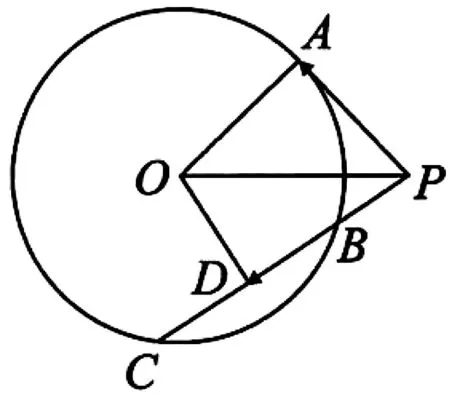
图1

点评:本题解法多样,灵活性强,综合性强,考查直观想象、理性思维等素养,试题重基础、重能力,在考查平面几何和三角知识的同时,有效考查了数形结合思想和转化与化归思想,为考生提供了多层次的思考空间.
二、对填空题的评析
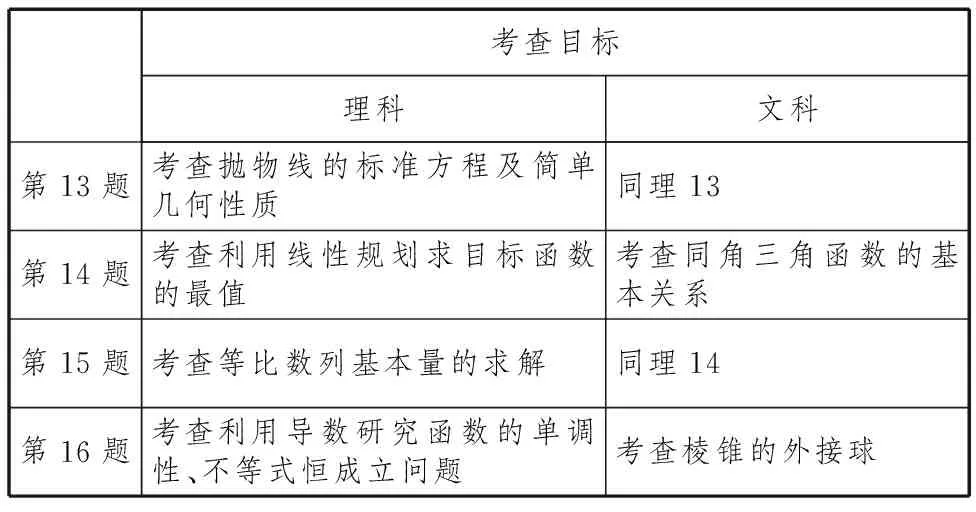
考查目标理科文科第13题考查抛物线的标准方程及简单几何性质同理13第14题考查利用线性规划求目标函数的最值考查同角三角函数的基本关系第15题考查等比数列基本量的求解同理14第16题考查利用导数研究函数的单调性、不等式恒成立问题考查棱锥的外接球
其中理科第16题、文科第16题值得认真研究和品味.
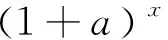
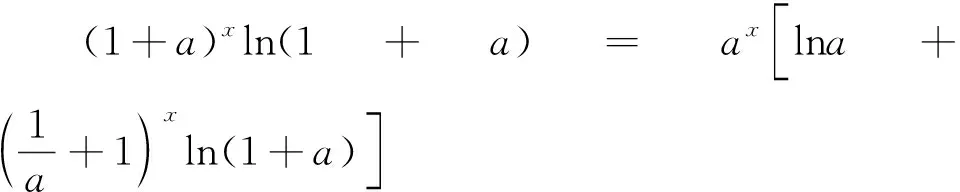
点评:本题考查参数的取值范围问题,试题看似复杂,但基本原理简单,考查了函数递增的充要条件,充分说明了高考更注重对基础知识、基本思想的考查,紧扣课程标准.
例5 (文16)已知点S,A,B,C均在半径为2的球面上,ΔABC是边长为3的等边三角形,SA⊥平面ABC,则SA=________.
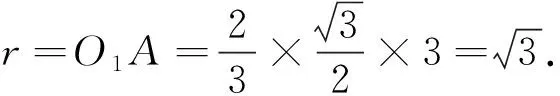
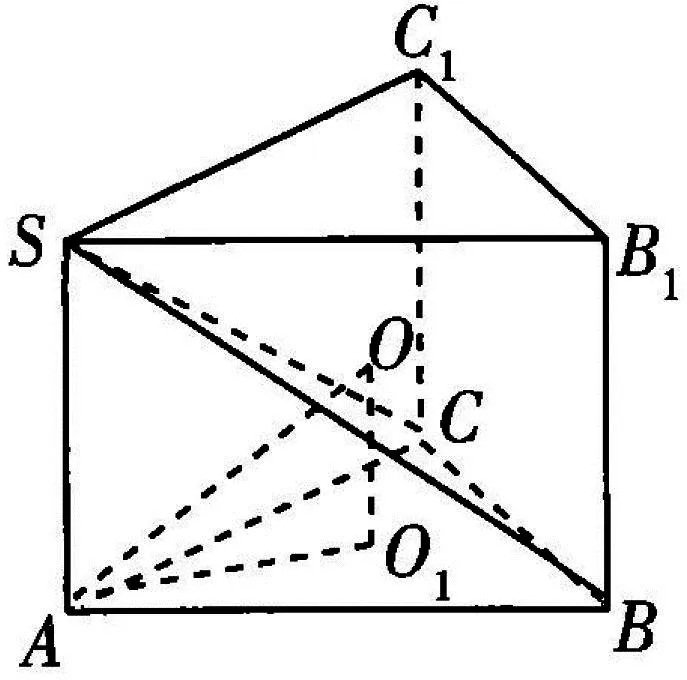
图2
点评:棱锥的外接球问题是高中数学的重点内容,难点在于找到外接球球心的位置,本题主要考查考生的空间想象能力和运算求解能力,试题简洁明了,注重考查基础知识,属于常规题,增强了考生自信心,促进考生正常发挥,同时也反映出高考数学更加注重对基础知识的考查,而不是一味变花样地增加难度.
三、对解答题的评析
1.统计题——中规中矩送大礼
本题考查样本平均数、方差,利用样本数据特征估计总体,体现了数据分析、数学建模、数学运算等核心素养.本题与考生平时的训练题极为相似,绝大多数考生当笑纳“大礼”.
2.三角题——平平淡淡考功底
理科三角题考查利用正弦定理、余弦定理解三角形,三角形的面积公式,考查数形结合思想、转化与化归思想,体现了数学运算、逻辑推理等核心素养.数学功底扎实的考生对于本题所用的破解“招法”谙熟于心,顺利求解当不成问题.
3.数列题——常见题型稳情绪
文科数列题考查等差数列的通项公式、分段数列求和,考查转化与化归思想、分类讨论思想,体现了数学运算、逻辑推理等核心素养.本题题型常规,跟考生平时的训练题类似,彰显了命题者对考生的人文关怀,有利于激发考生的解题兴趣,稳定考生的情绪.
4.立体几何题——想说爱你不容易
理科题考查直线与平面平行的判定、平面与平面垂直的判定、二面角的正弦值的求解;文科题是理科题的姊妹题,考查直线与平面平行的判定、三棱锥的体积.这两题考查转化与化归思想,体现了直观想象、逻辑推理、数学运算等核心素养.本题貌似简单,其实暗藏玄机,考生求解起来并不顺利,从考试结果看,该题得分率偏低.
5.解析几何题——精打细算求真理
本题考查直线与椭圆的位置关系、椭圆中的定点问题等,考查数形结合思想、转化与化归思想,体现了逻辑推理、数学运算等核心素养.第(1)问由点A在C上得出b2的值,结合离心率和a2=b2+c2求出a2的值,进而得出C的方程;第(2)问由题意知直线PQ的斜率存在且不为0,设出直线PQ的方程和P(x1,y1),Q(x2,y2),与椭圆方程联立,由根与系数的关系得出x1+x2和x1x2,写出直线AP的方程求出点M的纵坐标yM,同理易得点N的纵坐标yN,通过计算得出yM+yN=6,进而得出MN的中点为定点(0,3).本题第(2)问运算量较大,有一定的难度,具有较好的区分和选拔功能.
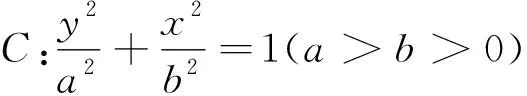
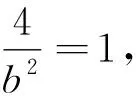
(2)如图3,由题意知,直线PQ的斜率存在且不为0,设lPQ:y-3=k(x+2),P(x1,y1),Q(x2,y2),由
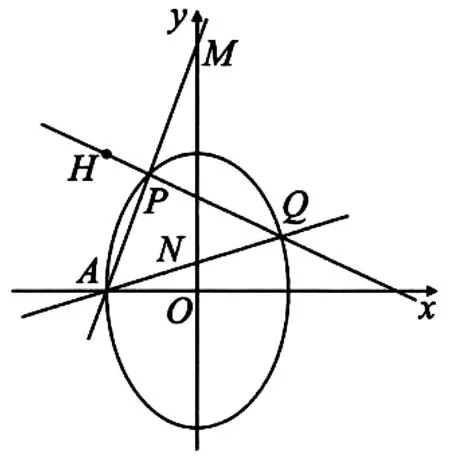
图3
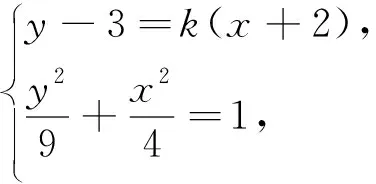
点评:本题与2022年全国乙卷解析几何题相似,都考查圆锥曲线的定点问题,但难度较2022年有所降低,主要考查理性思维、数学探索学科素养,考查直观想象和数学运算能力,通过本题也能看出2023年高考数学在出题风格和设问方式上与2022年类似,要想得高分,应注重基础知识和基本思想、基本方法,多研究近几年的高考题,而不是一味地刷题,追求难度,从而真正实现“双减”又高效备考的目的.
6.函数与导数题——分段得分巧智取
理科第21题函数与导数题考查导数的几何意义、函数图象的对称性、利用导数研究函数的极值.第(1)问考查曲线在某点处的切线;第(2)问由曲线的对称性求参数的值;第(3)问由函数存在极值求参数的取值范围.
文科第21题函数与导数题是理科第21题的姊妹题,考查导数的几何意义、利用导数研究函数的单调性.第(1)问同理科第(1)问;第(2)问由函数的单调性求参数的取值范围,难度明显降低,切合文科考生的数学实际.
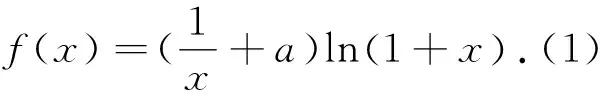
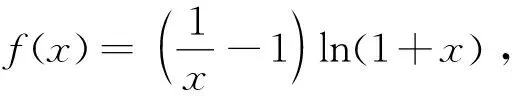
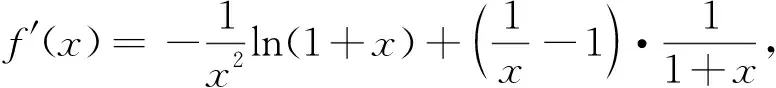
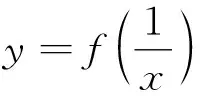
①当a≤0时,2a-1<0,当x>0时,h′(x)<0,所以h(x)在(0,+∞)上单调递减,所以当x>0时,h(x) 点评:本题以含参数的复杂函数为载体,通过对切线方程、函数图象的对称性及函数极值点的考查,渗透着数学中大胆猜测,小心验证的基本思维方式.重点考查分类讨论思想,突出对数学学科基本概念、基本原理的考查,强调知识之间的内在联系,注重本原性方法,淡化特殊技巧,强调对通性通法的深入理解和综合运用,促进学生将知识和方法内化为自身的能力. 7.二选一选考题——中规中矩合情理 选考题第22题考查极坐标方程与直角坐标方程的互化、参数方程与普通方程的互化、直线与圆的位置关系.选考题第23题考查绝对值不等式的解法、不等式组确定的平面区域的面积.这两选考题意在考查考生的运算求解能力、逻辑推理能力及函数与方程思想、转化与化归思想、数形结合思想等,难易适中,题型常规,与考生平时的训练题类似,考生志在必得. 总之,2023年高考数学全国乙卷试题闪光着理性思维的光芒,以问题情境设置为载体,考查核心价值和能力素养.试题聚焦学科主干知识,突出学科关键能力,关注社会生活和实践应用,很好地体现了“一核四层四翼”的考查要求,很好地把握了稳定、改革与创新之间的关系,彰显了立德树人价值引领与核心素养育人导向.