是“错题”,还是“正解”?——
——离散型分布列取值概率可以为0吗?
王楷文
安徽省合肥市第六中学 (230001)
一、问题发现
在学习了离散型分布列时,教辅资料中有这样一道题:
设p为非负实数,随机变量X的分布列为

X012P12-pp12
则E(X)的最大值为________,D(x)的最大值为________.
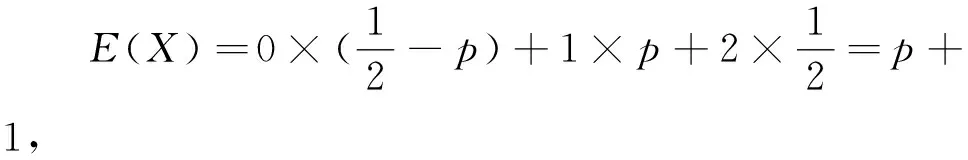
根据古典概型的定义,知当p=0时,离散型随机变量X=1对应的试验结果没有发生,即当p=0时这个试验的结果只有两个结果X=0与X=2,而没有X=1这个结果,此时分布列表中的X=1就多余了,是这个题目有错误,还是我们对于教材内容的理解不到位呢?笔者所在学校使用的是北师大版教材,2019年12月第1版(2022年7月第5次印刷)的选择性必修第一册第198页关于离散型分布列的性质写道:(1)pi>0,i=1,2,…,n,…;(2)p1+p2+…+pn+…=1.由此看出,北师大版教材关于离散型随机变量取值的概率不能为0,基于此认识,知此题是错题.
但人教A版选择性必修第三册(2020年3月第1版)第58页关于分布列的性质介绍如下:(1)pi≥0,i=1,2,…,n;(2)p1+p2+…+pn=1.显然教材给出的随机变量取值的概率是pi≥0,i=1,2,…,n,而不是pi>0,i=1,2,…,n,…,这种情况说明是的确存在随机变量取值可以为零的情况,还是“pi≥0,i=1,2,…,n”中等号是多余的呢?基于人教版教材中对于离散型随机变量的定义,如果离散型随机变量的某一个取值对应的事件是存在的,且其概率为零,那么上述解答就是正确的.
面对如此现象,作为教师该如何处理呢?
二、问题解决
由于一个试验的每一个试验结果称为样本点,而试验结果究竟是什么,与试验所要求是什么结果有关,如抛掷一枚质地均匀的骰子,如果按照正面向上个数是什么,则试验的结果就有6个,即样本点有6个;如果按照骰子向上的点数是奇数还是偶数,则试验的结果就有2个:向上的点数是奇数与向上的点数为偶数,即样本点有2个,由此可知,将一个试验的所有基本事件按照一定的标准进行分类整合也可产生新的样本点,由于每一个样本点ω都能用唯一的实数X(ω)与之对应,则称X为随机变量,例如,抛掷一枚质地均匀的骰子,随机变量可以是X=1,2,3,4,5,6,也可以是Y=0,1(其中0代表向上的点数为偶数,1代表向上的点数为奇数),基于此认识,请看例子:在(1,5)中取一个数,可将试验结果分为三类(1,3),3,(3,5),不妨记作随机变量X=1,2,3(其中1表示区间(1,3),2表示点3处,3表示区间(3,5)处),则由几何概型知,P(X=3)=0,但X=3对应的事件是有可能发生的,即概率等于0的事件不代表不可能发生.
正是因为我们可以将几何概型试验的结果按照一定的标准进行分类整合若干部分作为随机变量,而每一部分的试验结果均可以用一个数字表示,这样获得的离散型随机变量的取值概率有可能为零,且这个变量取值对应的试验结果也是有可能发生的,基于此认识,我们有理由认为上述问题的解答是正确的.
三、问题思考
在教学中,遇到一些困惑问题是正常的,但面对困惑时,我们教师是客观冷静地弄清楚问题的真相,还是一棍子打死,武断地认为此题是错题,这两种截然不同的态度,反映了我们教师两种对待教学的态度,是认真地作潜心研究,还是不加深思认为是错题?古人云:“师者,传道授业解惑也”,这句话教师都能耳熟能详,但遇到困惑时,往往回避的多,深入研究的少,从而会造成教学的“冤假错案”,如,本题是没有错误的,如果教师告诉学生是错误的,那么就造成混淆是非,之所以会出现此种现象,是因为教师有些经验是不成熟导致的,事实上,受思维定势的影响,故步自封,我们不少自认为成熟的经验却是片面的、不成熟的,对此,不少教师蒙在鼓里,却自己不知道,如根据北师大教材介绍的离散型随机变量的性质pi>0,i=1,2,…,n,…,轻易判断此题是此题,就是有力的例证.
俗话说:“身教胜于言教”、“榜样的力量是无穷的”,所以在教学中教师要做到为人师表,以给学生树立榜样,真正做到立德树人.况且,在倡导学生深度学习的今天,培养学生学会思考的习惯,是当下教师教育教学的职责,为此教师更应该做到深度学习,试想:如果一个教师在教学中遇到疑难问题需要深入研究时,却回避了之,那么怎能引导学生进行深入思考呢?学生的核心素养如何发展呢?实际上,只有让学生参与问题研究的情境过程中,才能真正发展学生的素养,对此,应引起我们教师深思!
总之,在教学中遇到一时难以化解的问题,教师摒弃“那种没有经过一番深度思考,而仅凭经验感觉行事,主观臆断是非曲直”的做法,而应该以积极的心态应对,通过查资料、与同行研讨、深思细悟、倾听学生想法等多方论证,将问题的来龙去脉弄清楚,给学生一个明白的解释,若是题目错,要讲出错的原因,若是解答正确,则解答正确的依据是什么,只有这样,我们的教学才能谈得上有深度、有品位、有素养的教学.

