二项式定理题型破解思路与策略

刘千吉

哈尔滨师范大学教师教育学院

二项式定理的起源最早可以追溯到古希腊时期的欧几里得《几何原本》,而后到了1654年,数学家帕斯卡,建立了“一般正整数次幂”的二项式定理,并研究了二项式系数的性质和规律.1665年,牛顿在前人的研究成果上把二项式定理推广到n为分数与负数的情形,创立了现代的“二项式定理”[1].二项式定理的发展不仅丰富了数学知识体系,也为解决实际问题提供了有力的工具.

在历年高考试题中,二项式定理也是考查的热点内容之一,常以客观题形式出现,例如求二项展开式中的特定项或特定项系数问题、与二项展开式中的系数和有关的问题、利用二项式定理处理整除问题以及计算近似值的问题等.随着新课标的修订与新高考改革,数学教学与考试更加注重核心素养与思维能力[2].针对有关二项式定理的问题,学生需要通过排列组合从本质上理解二项展开式的通项公式,了解二项式系数的性质,掌握赋值法在求解二项展开式系数和问题中的巧妙运用,这样才能在面对此类问题时得心应手、游刃有余.

1 通过排列组合理解二项展开式通项公式的本质

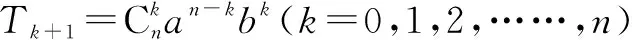
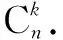
通过排列组合理解二项展开式通项公式的本质,能够帮助我们更好地解决如下问题.

1.1 求二项展开式中的特定项或特定项系数

类型1：求形如(a+b)n(n∈N*)的式子中与特定项相关的量(如求常数项、特定项).

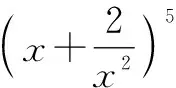
分析：本题要求二项展开式中x2项的系数,比较简单,可以直接写出二项展开式的通项,令x的次数为2从而求出该项,体现了通项公式的作用.

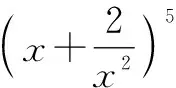
类型2：求形如(a+b)m(c+d)n(m,n∈N*)的式子中与特定项相关的量.

分析：本题是两个二项式乘积求展开式中特定项的系数,针对这类问题依然可以先分别写出两个二项式的通项公式,再相乘得到这两个二项式乘积的通项公式,最后找出其中特定项的系数.

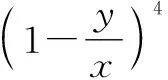
类型3：求形如(a+b+c)n(n∈N*)式子中与特定项相关的量.

例4(x+y-2z)5的展开式中,xy2z2的系数是______.

分析：本题是求三项展开式中特定项的系数,因此二项展开式的通项公式并不能直接运用,有的方法是将三项式转化为二项式,例如将x+y-2z化为“x+y”与“-2z”和的五次方,然后运用二项展开式的通项公式展开,再对x+y的相应次方展开.此种方法确实将三项式转化为了二项式,从而使其可以使用二项展开式的通项公式求解,但无疑增加了求解难度和计算量.如果我们充分理解了二项展开式通项公式的本质,能够运用排列组合写出多项式的通项公式或直接写出其特定项,这道题目则会变得非常简单.

例5(1+x+x2)3的展开式中,x2的系数是______.

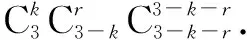
1.2 处理整除问题

例6设c∈Z,且0≤c≤13,若531 024+c能被13整除,则c等于 ______.

1.3 计算近似值问题

例7利用二项式定理计算1.056,则其结果精确到0.01的近似值是 ( ).

A.1.23 B.1.24 C.1.33 D.1.34

分析：利用二项式定理计算近似值依然可以借助于二项展开式的通项公式,将1.056化为一个容易计算的值与另一个远远小于其值的和或差的形式,从而通过尽可能少地计算二项展开式中的前几项来达到近似计算的效果.

2 二项展开式系数和问题中的破解

“赋值法”普遍适用于恒等式,是一种重要的方法.对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R)的式子求其展开式的各项系数之和,常用赋值法,令x=1即可;对形如(ax+by)n(a,b∈R)的式子求其展开式各项系数之和,只需令x=y=1即可.

例如,对于(cx+d)7(c,d∈R) 的式子,其展开式各项可以写成a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6+a7x7形式.

令x=1,可得各项系数和

a0+a1+a2+a3+a4+a5+a6+a7.

①

令x=-1,可得

a0-a1+a2-a3+a4-a5+a6-a7.

②

①+②=2a0+2a2+2a4+2a6.(2倍偶次项系数和)

①-②=2a1+2a3+2a5+2a7.(2倍奇次项系数和)

例8(2022年高考浙江卷)已知多项式(x+2)·(x-1)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a2=______,a1+a2+a3+a4+a5= ______.

分析：本题第一问属于求展开式中x2项的系数问题,可以运用通项公式计算.第二问先求展开式各项系数和a0+a1+a2+a3+a4+a5,再减去a0.各项系数和可以通过对x赋值为1求得,a0可以通过对x赋值为0而求得.

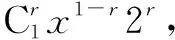
(2)对x赋值1,求得a0+a1+a2+a3+a4+a5=0;对x赋值0,求得a0=2.

所以a1+a2+a3+a4+a5=0-2=-2.

面对新高考更加注重对数学核心素养的考查,在二项式定理方面,更需要学生运用排列组合知识从本质上理解二项展开式的通项公式,以及掌握赋值法在求解二项展开式系数和问题中的巧妙运用.把握原理与核心才能以不变应万变,高效地解决二项式定理相关的各种题型,并且真正促进学生素养与思维的发展.