EMA摩擦前馈补偿的模糊自抗扰控制方法研究

石照耀, 张攀, 林家春

(北京工业大学 精密测控技术与仪器工程技术研究中心,北京 100124)

0 引 言

由永磁同步电机+减速器+控制器集成的机电执行器(electromechanical actuator,EMA)广泛应用在机器人[1]、柔性关节[2-3]、航空航天[4]、空间机械臂、数控机床等领域。EMA中减速器主要有3种类型,分别为:RV减速器、行星减速器、谐波减速器。在精度要求高,负载不是特别大的场合多使用谐波减速器。谐波减速器具有噪声小、体积小、重量小、侧隙回差小以及承载能力高、传动精度高、减速器比高、效率高,“四高”和“四小”的优良特性[3]。影响谐波减速器传动精度的因素主要有:间隙、摩擦、刚度、传动误差。如何最大程度的消除非线性摩擦对EMA控制精度的影响,一直是众多学者研究的热点之一[3-5]。

国内外大量学者对EMA的控制方式和谐波减速器的非线性摩擦补偿做了大量研究。Spong等[6]首次提出了柔性关节的动力学建模方法。石崟等[7]引入了弹流润滑、非线性刚度因素建立了速度、负载转矩和温度参数耦合的谐波减速器模型,并使用遗传算法对某型号的谐波减速器进行了参数辨识,并通过实验验证了该模型的准确性。H.D.Taghirad等[8]建立了谐波减速器的动力学模型,在高速和低速下对摩擦损耗进行了建模,通过仿真分析对建立模型的特性进行了研究。文献[9]建立了包含运动误差、摩擦特性、柔性特性的谐波减速器模型,并使用三次多项式描述摩擦模型。文献[10]在频域方面对伺服系统中的摩擦模型进行参数辨识,使用方波信号激励,通过分析系统响应中的高频谐波,辨识出系统的摩擦模型参数,并在控制器中进行补偿。文献[11]将谐波减速器和轴承的摩擦视为总扰动,并构建扰动观测器进行估计,通过前馈补偿的方式融入PID控制器中,通过仿真和实验的方法验证了该策略的有效性。文献[12-13]综合性的介绍了机械系统中十几种摩擦模型,对不同摩擦模型的特点和适用范围进行了详细描述。

文献[14]建立EMA的指数摩擦模型,使用摩擦前馈补偿的方法提高了角度跟踪精度。文献[15]设计了基于摩擦前馈补偿的控制器,并通过实验验证了摩擦前馈补偿的有效性,提高了角速率误差。文献[16]建立了简化的齿轮伺服系统动力学模型,通过转速-转矩实验测得了系统的Stribeck曲线,提出一种自适应摩擦补偿方法,提高了系统的位置跟踪性能。

目前,EMA控制系统中常用矢量控制+PI(D)控制器构成的三闭环控制策略。PID控制器是一种线性控制器,具有结构简单,算法简单,控制参数少,易于工程实现的优点,在工业界仍占据着主导地位[17]。但PID控制器误差信号的取法会使系统初始误差较大,容易引起超调。使用差分信号近似代替微分信号,这种处理方式对噪声信号进行了放大,造成微分信号失真严重。对比例环节、积分环节、微分环节做线性组合,继而作用于被控对象,这种处理方式很难解决快速性与超调之间的矛盾。韩京清先生在深入研究现代控制理论并结合PID基于误差消除误差的控制精髓基础上,提出了自抗扰控制(active disturbance rejection control,ADRC)技术[18-19]。ADRC控制技术不依赖被控对象数学精确模型,将系统未建模部分、外部扰动以及传统方法不易处理的复杂非线性因素和时变因素等耦合而成的不确定部分作为系统的“总扰动”,利用系统的输入和输出构造扩张状态观测器,在线估计“总扰动”并在反馈控制中进行补偿[20-22]。

自ADRC技术诞生后,已有大量科研、工程人员将ADRC应用于电机控制领域。文献[23]设计了一种永磁同步电机(permanent magnet synchronous motor,PMSM)模糊ADRC系统,通过仿真和实验验证了这种控制方法的响应快速性、无超调、控制精度高的特点。文献[24]根据PID和模糊控制原理,设计了变论域自适应模糊 PID 复合控制策略,实现了控制参数自整定和控制规则的自调整。

文献[25]提出了一种PMSM调速系统模型补偿的ADRC控制方案,通过参数辨识确定系统的部分模型,减小扩张状态观测器对扰动估计的压力,提高扰动估计精度。文献[26]设计一种新型非线性函数,在此基础上提出一种改进型ADRC控制器。文献[27]设计一种新型非线性函数,代替ADRC中的非线性函数实现了快速、准确的对扰动进行估计和补偿。文献[28]提出了一种PMSM位置-电流双环控制策略,仿真和实验结果表明,复合型ADRC控制器对负载转矩、电机参数变化等扰动具有较好的抑制作用。

为了减小非线性摩擦特性对控制精度的影响,本文提出基于模糊ADRC(Fuzzy-ADRC)控制器的EMA非线性摩擦建模及补偿的方法。在PMSM和谐波减速器的模型基础上推导摩擦力和转矩电流的关系。测试不同转速下的转矩电流,使用小波+卡尔曼联合滤波的方式对测试数据进行处理。建立库伦+粘滞+Stribeck摩擦模型,使用三次高斯拟合的方式获取转速与转矩电流的函数关系,基于ADRC原理和模糊控制原理构建Fuzzy-ADRC控制器,并在Fuzzy-ADRC中加入非线性摩擦前馈补偿,提高EMA的控制精度,通过实验证明该方法的可行性。

1 PMSM数学模型

EMA中主要包括PMSM和谐波减速器两大非线性因素。PMSM和谐波减速器主要通过转矩电流耦合在一起。PMSM常用矢量控制(vector control,VC)又称磁场定向控制(field orientated control,FOC)和直接转矩控制(direct torque control,DTC),由于DTC中使用Bang-Bang控制产生转矩脉动,所以在高性能的控制方式中FOC控制方式较多[29]。在不影响PMSM控制性能的前提下,为简化分析,做如下假设:忽略铁心饱和效应;不计电机中涡流和磁滞损耗;绕组中的电流为理想三相对称的正弦波电流。FOC控制策略下PMSM的数学模型主要由电压方程、磁链方程、电磁转矩方程、机械方程组成,在d-q旋转坐标系下,PMSM数学模型表达式[30-31]为:

(1)

其中:Rs为相电阻;id、iq、ud、uq、Ld、Lq、ψd、ψq分别为d-q轴电流、电压、电感、磁链;pn为极对数;id、iq又称转矩电流、磁链电流;Te为电磁转矩;J为转动惯量;TL为负载转矩;B为阻尼系数;ψf为永磁体磁链;ω、ωr分别为电角速度和机械角速度。对于表贴式PMSM,有Ld=Lq=Ls,使用id=0控制方式,式(1)中电磁转矩方程可简化为

Te=1.5pnψfiq。

(2)

2 谐波减速器传动模型

精密谐波减速器一般由柔轮、刚轮、波发生器组成,如图1所示。3个器件中可以任意固定其中一个,另外2个作为输入和输出,实现增速或减速目的。EMA中通常将刚轮固定,转子与波发生器连接,柔轮作为从动轮。波发生器通常由薄壁柔性滚动球轴承和标准椭圆凸轮组成,波发生器装入柔轮后,柔轮变形为椭圆形,柔轮的外圈轮齿和刚轮的内圈轮齿部分接触,一般有30%左右齿轮处于啮合状态。

图1 谐波减速器结构图Fig.1 Structure diagram of harmonic drive

谐波减速器工作时,波发生器为主动元件,波发生器转动时使柔轮发生可控的弹性变形实现运动和动力传递。波发生器连续转动时,柔轮节圆上的任一点会形成一个上下左右相对称的和谐波,故称为“谐波”。通常柔轮齿数比刚轮齿数少2个,其传动比为i=-Z2/(Z1-Z2),Z1、Z2分别为刚轮和柔轮的齿数。

谐波减速器在力矩传递过程中存在非线性摩擦损耗,根据传递过程中摩擦环节建立谐波减速器的非线性摩擦传动模型如图2所示。

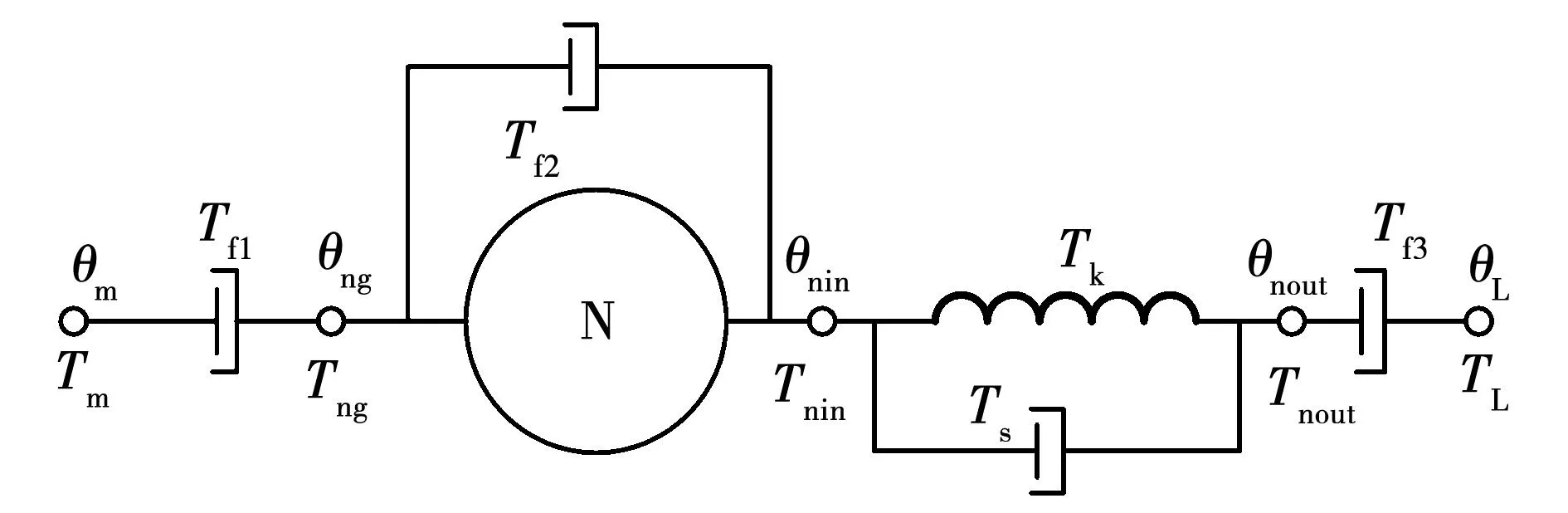
图2 谐波减速器传动模型Fig.2 Harmonic drive transmission model

图2中:Tf1为波发生器上的摩擦;Tf2为柔轮与刚轮之间的摩擦;Tf3为柔轮上的摩擦;θm为电机转子(波发生器)位置;Tm为波发生器的力矩;θng、Tng、θnin、Tnin、θnout、Tnout为谐波减速器模型的中间变量;θm为电机转子(波发生器)位置;TL为柔轮输出力矩;θL为柔轮位置;Tf为谐波减速器的摩擦力矩,大小为Tf=Tf1+Tf2+Tf3,低速重载下负载端摩擦力矩Tf3比高速轻载下电机端摩擦力矩Tf1小得多,可以忽略不计,即Tf3= 0;Tnout为等效的弹簧阻尼力;TL是负载转矩,TL=Tnout=Tk+Ts,TL是与传动误差相关的函数,即f(θ)=TL。谐波减速器传动误差的表达式为

(3)

由以上分析得,谐波减速器输入力矩、摩擦力矩、输出力矩之间的关系为:

(4)

式中KL为谐波减速器的刚度系数,匀速时,电机中的转矩与谐波输入的转矩相等,即Tm=Te。如果将波发生器的转动惯量和电机转子的转动惯量视为整体,将柔轮的转动惯量和负载的转动惯量视为整体,可以将EMA视为二质量系统。Jm为电机转子转动惯量,JL为负载端的转动惯量,电机转矩Te与波发生器转矩Tm的关系为:

(5)

由式(2)、式(4)、式(5)可得谐波减速器非线性摩擦力Tf的表达式为

(6)

负载时Tf的表达式又可表示为

(7)

式(6)、式(7)的主要差别在于是否考虑传动误差的影响,当空载或负载较小时传动误差因素较小可忽略。负载较大时,由于弹性变形的原因会导致传动误差加大。

EMA空载并匀速运行时式(6)可简化为

Tf=1.5pnψfiq。

(8)

即摩擦力等于电机的电磁转矩。施加较大负载并匀速运行时,式(7)摩擦力的表达式可简化为

(9)

库伦+粘滞+Stribeck模型描述摩擦力[12]可表示为

(10)

式中:Fc为动摩擦力矩,即库伦摩擦力;Fs为Stribeck摩擦力矩,即最大静摩擦力;v为系统转速;vs为Stribeck速度;σs为Stribeck模型参数。对于σs的取值,Bo和Pavelescu将σs的取值范围设定为0.5～1之间[32],有些学者常取σs=1或σs=2。当σs=1时得到Tustin模型[33],当σs=2时得到Gauss指数模型[34]。

当使用Tustin经验模型描述Stribeck现象时,σs为1。库伦+粘滞+Stribeck模型曲线如图3所示。

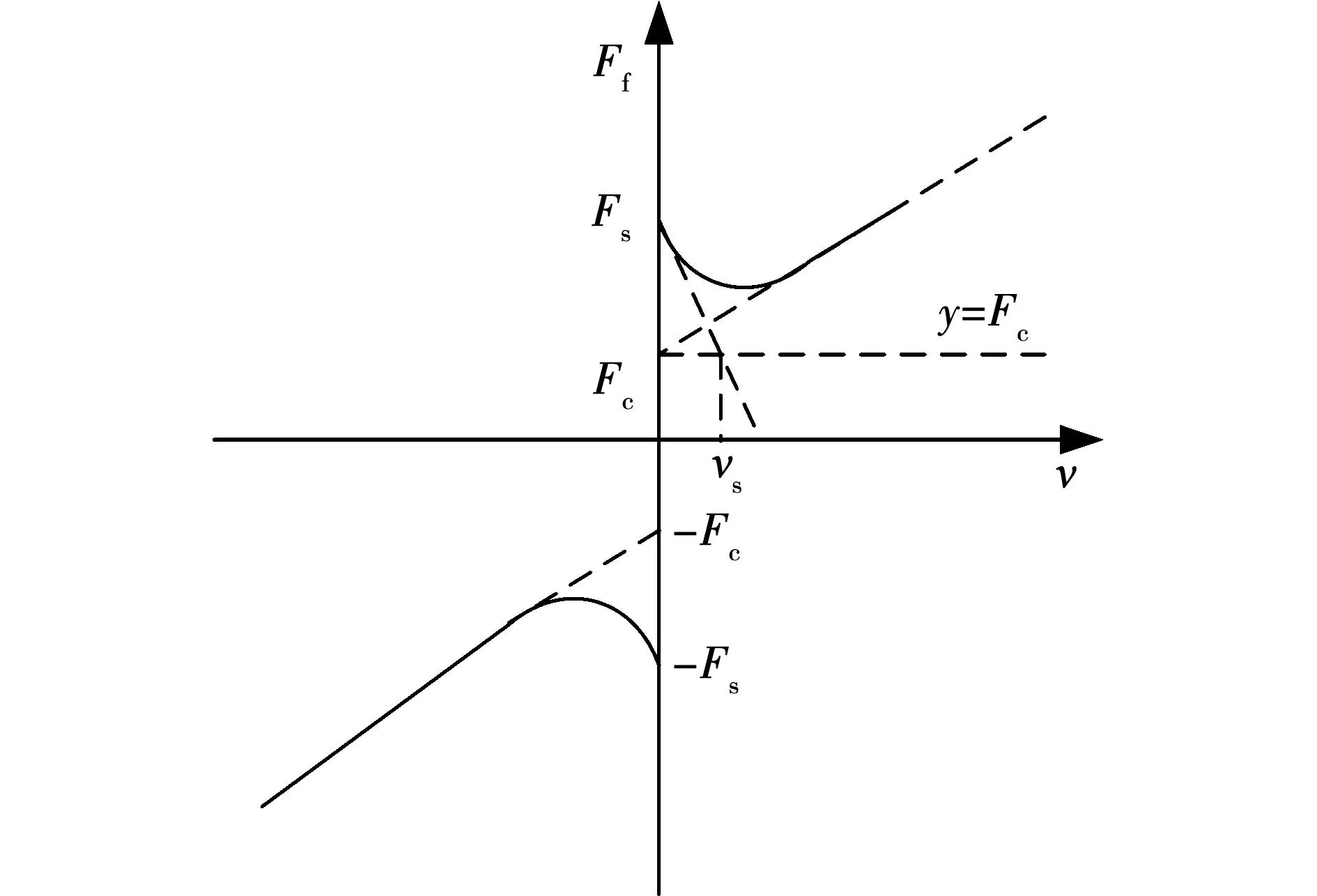
图3 库伦+粘滞+Stribeck模型Fig.3 Coulomb+Vscosity+Stribeck model

根据非线性摩擦力矩与转速的关系曲线,通过拟合的方法可以将模型的低速段和高速段大致拟合为直线,即正斜率线性段和负斜率线性段。负斜率线性段主要由模型中的指数项产生,描述系统从静止状态到缓慢运动过程中所产生的摩擦力。正斜率线性段主要表现为粘滞摩擦,斜率为粘滞摩擦阻尼系数B。负斜率段与纵轴的交点Fs,即为最大静摩擦力。正斜率段与y轴的交点Fc,为库伦摩擦力。负斜率线性段与直线y=Fc的交点的横坐标vs即为Stribeck速度。

3 小波-卡尔曼滤波联合去噪

由式(8)可知空载匀速状态下通过测量转矩电流iq便可以测量得到摩擦力矩。测量时将电机转速从小到大逐次增加,获取转速与摩擦力矩的对应关系。在低速区时,需要减小速度增加梯度,多次测量。中高速区可以加大速度梯度。0～50 r/min之间,速度梯度为1 r/min,50～100 r/min之间,速度梯度为5 r/min,100～500 r/min之间,速度梯度为10 r/min,500～1 000 r/min之间,速度梯度为50 r/min。

假设EMA正转和反转过程中所受的摩擦力大小相同,本文仅测正转方向的摩擦力。通过测量不同转速下的转矩值,经过数据拟合得到转矩-转速曲线。在测量iq过程中,不可避免出现测量噪声和系统噪声的污染,这里使用小波+卡尔曼联合滤波的方法进行处理。经小波+卡尔曼联合滤波处理的数据具有更小的均方根误差和信噪比,互相系数更接近于1,能够更真实的反应信号的原始特征[35-37]。在某一速度下,将测量的数据使用联合滤波算法处理后,计算摩擦力矩的均值。以此获得不同转速下的摩擦力矩。

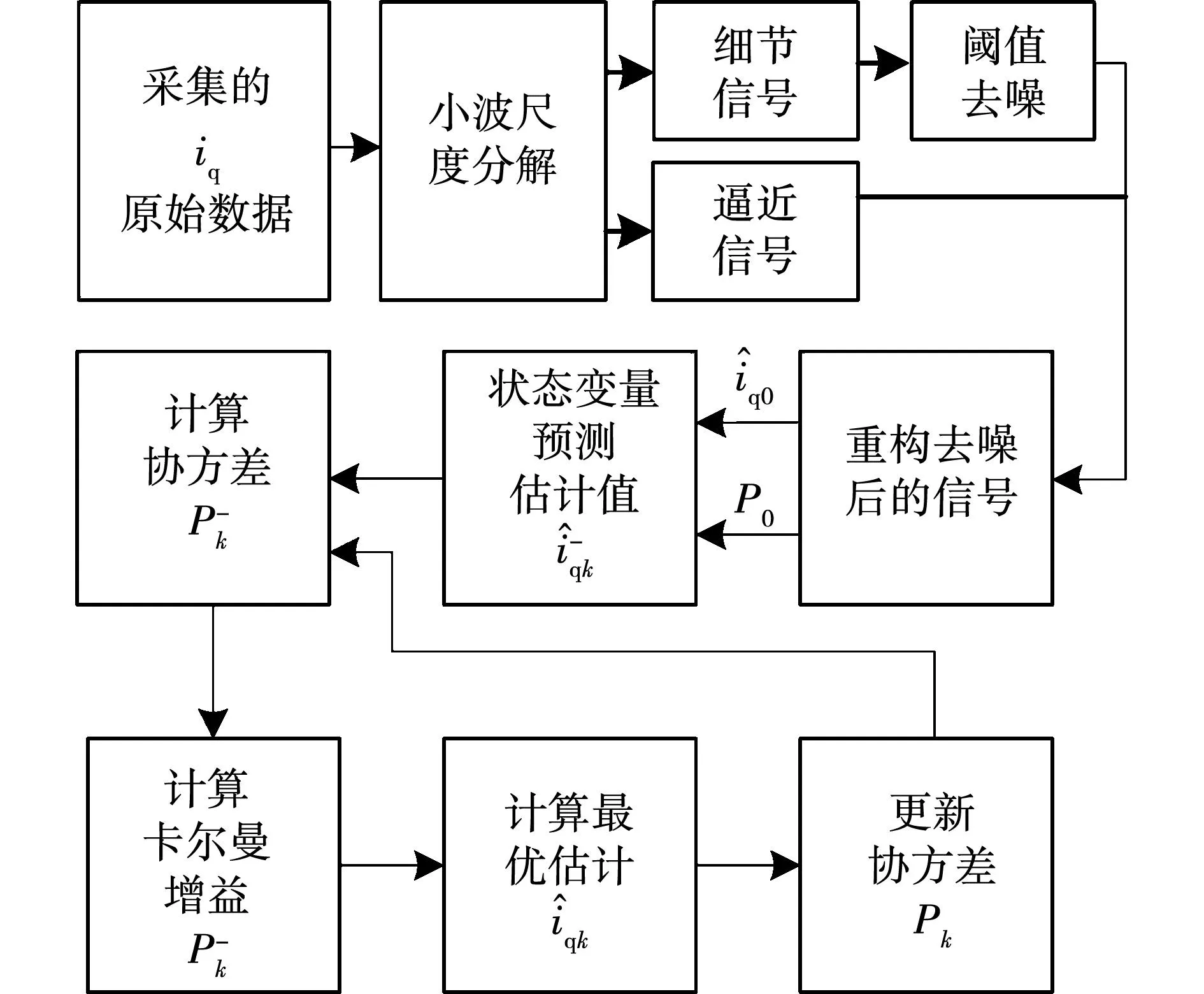
图4 小波卡尔曼滤波联合去噪算法Fig.4 Wavelet Kalman filter joint denoising algorithm

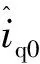
得到EMA转矩电流与转速的关系如图5所示。

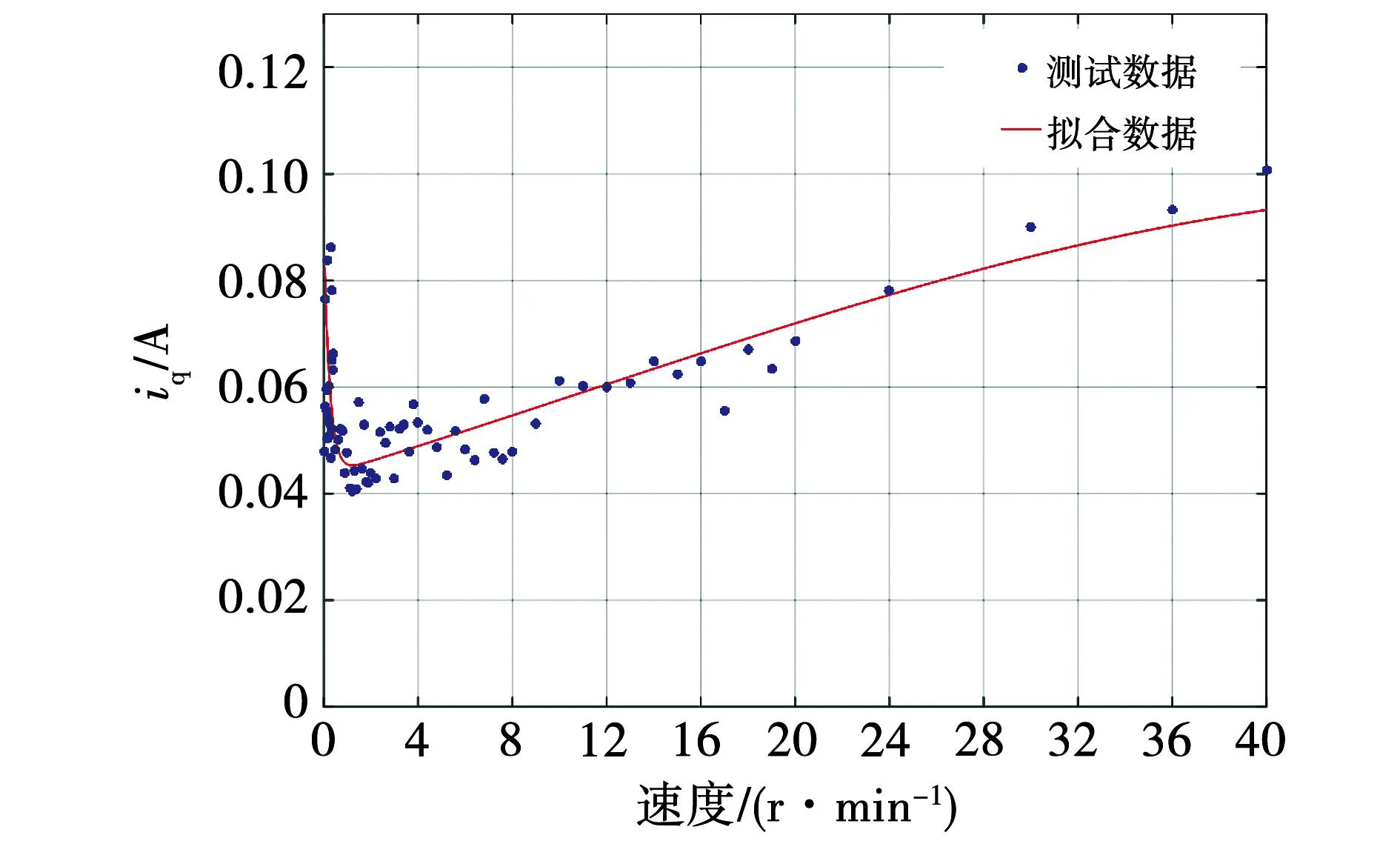
图5 摩擦力矩与转速曲线Fig.5 Friction torque and speed curve

图5中点为不同转速下获得的转矩电流,曲线为在MATLAB环境下使用高斯逼近法得到的拟合曲线。该曲线的表达式为

(11)

其中表1为an、bn、cn的具体数值。

表1 F(x)中参数表Table 1 Parameters of F(x)

为了减小谐波减速器摩擦特性对控制精度的影响,根据转速与转矩电流的函数关系进行摩擦模型补偿。

摩擦前馈补偿方法如图6所示。

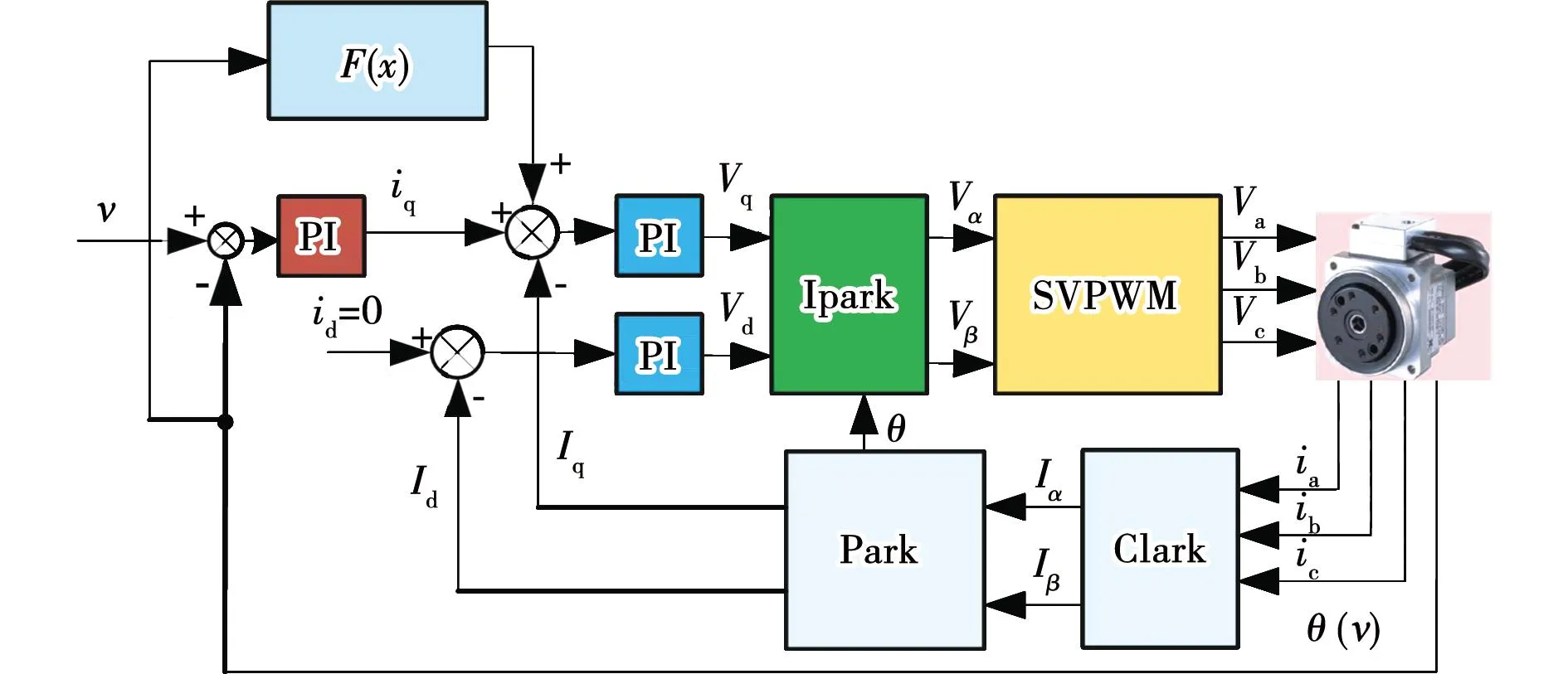
图6 非线性摩擦前馈补偿Fig.6 Nonlinear friction feedforward compensation

4 位置环二阶ADRC设计

4.1 ADRC数学模型

ADRC主要由跟踪微分器(tracking differentiator,TD)、扩张状态观测器(extended state observe,ESO)、非线性状态误差反馈(nonlinear states error feedback,NLSEF)组成。TD安排的过渡过程可以解决超调量与快速性之间相矛盾的问题,实现快速无超调跟踪输入信号。ESO对系统输出和内(系统未建模部分)外扰动进行观测,并在控制律中实时加以补偿有效的提高系统抗干扰能力。NLSEF为TD的输出和ESO的状态变量观测估计输出和非线性组合,同时NLSEF的输出与ESO对系统“总扰动”估计量组合后作用于被控对象。ADRC中的微分不同于PID中的微分,他不是放大“噪声”,而是抑制“噪声”。ADRC控制框图如图7所示。

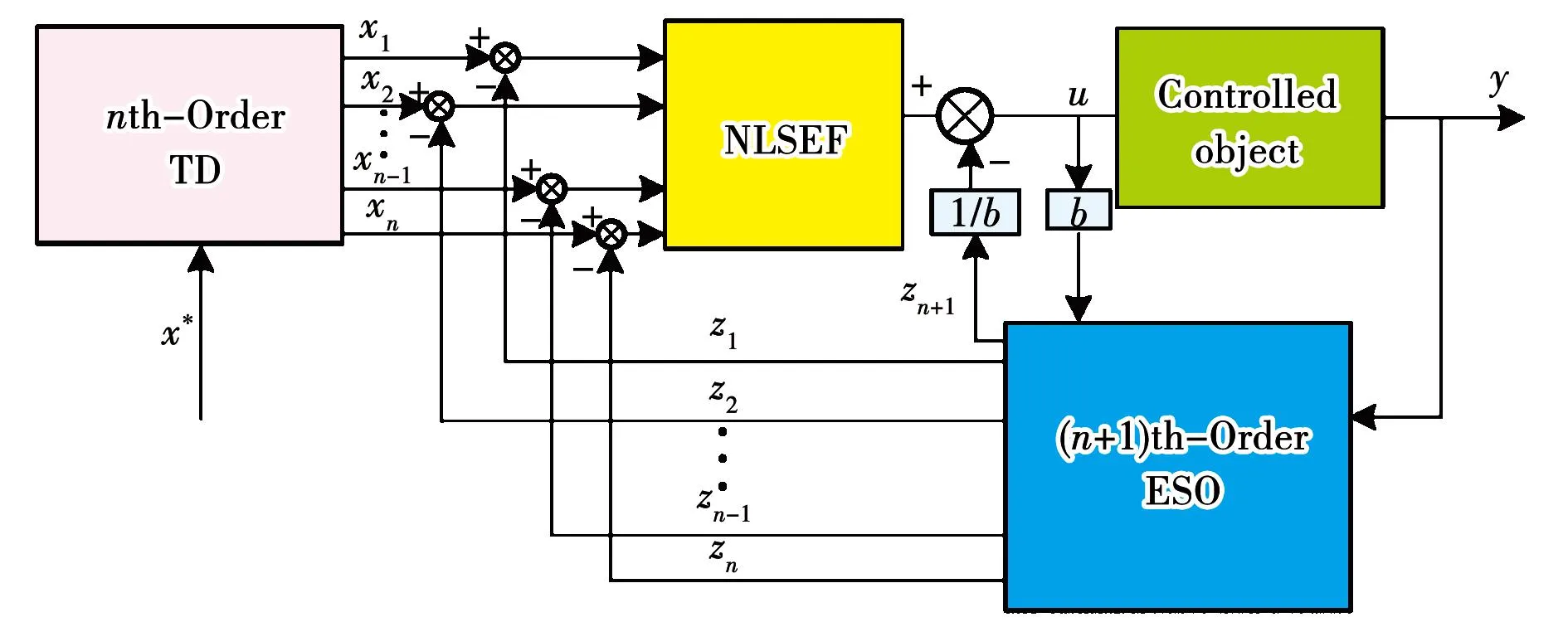
图7 ADRC控制框图Fig.7 ADRC control block diagram

二阶被控对象的状态方程表示为:

(12)

式中:u为系统控制量;b为系统控制量的增益;f1(·)为系统已知部分;f2(·)为系统未知部分,令w(t)=f1(x1,x2)+f2(x1,x2,t),那么w(t)就是系统“总扰动”。

典型的二阶ADRC表达式为:

(13)

为了将模糊控制引入位置环ADRC制器,这里将NLSEF加入误差的积分环节,NLSEF改写为:

(14)

TD中的最优综合控制函数fhan(·)以及fal(·)函数的表达式为:

(15)

(16)

式中:α为非线性因子;δ为滤波因子;e为误差变量。fal(·)函数具有“小误差大增益,大误差小增益”的特点。

4.2 EMA位置环ADRC设计

根据式(1)中的机械方程以及式(2)可以推导PMSM位置环的动态数学模型为

(17)

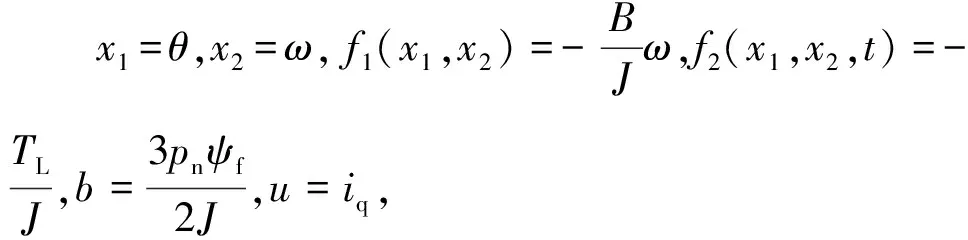
(18)

由此可以跟据式(13)～式(16)构造位置环二阶自抗扰表达式。位置环二阶ADRC控制框图如图8所示。

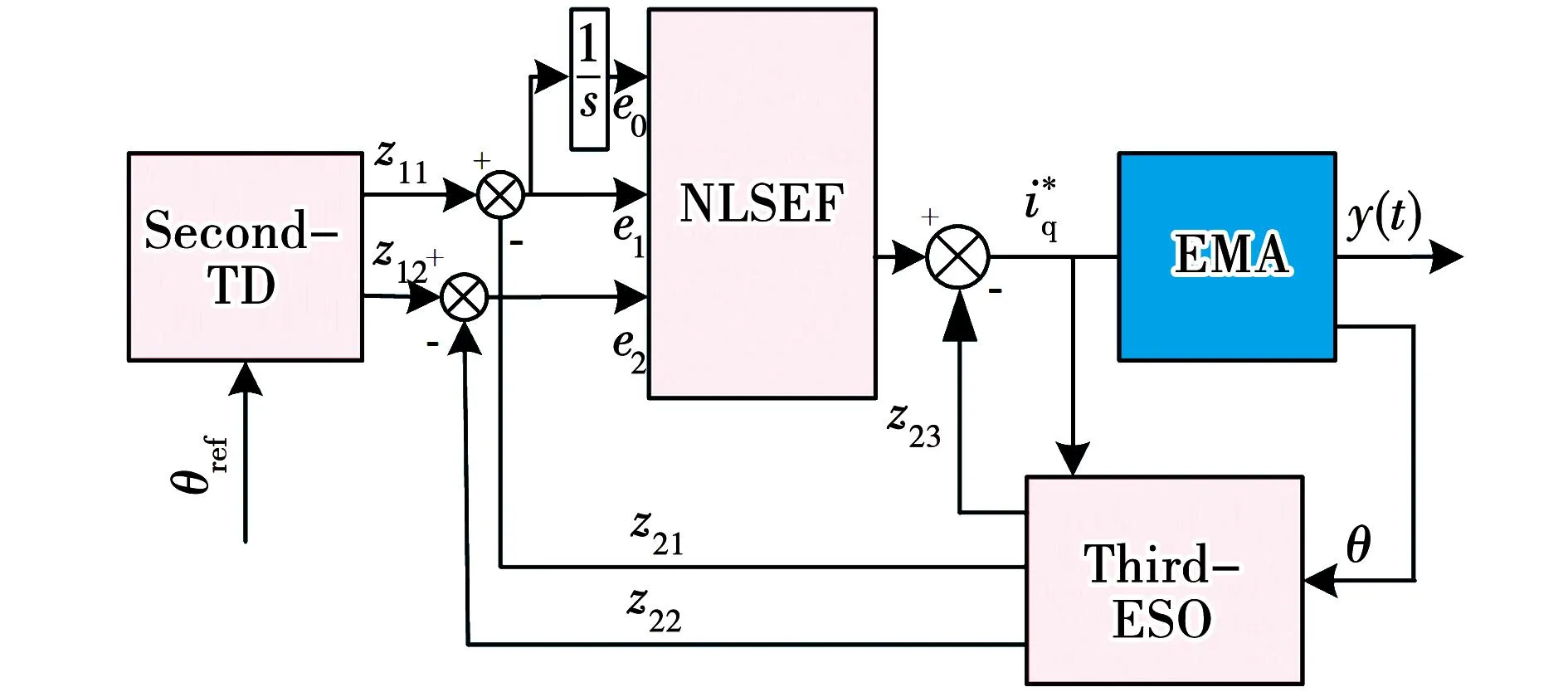
图8 位置环二阶ADRCFig.8 Position loop second order ADRC

4.3 EMA中Fuzzy-ADRC设计

ADRC控制参数的变化对系统控制性能影响较大,为了实现ADRC的自适应功能,在ADRC中加入模糊控制环节。NLSEF中待整定的参数β1、β0、β2和PID的控制参数相似,β1对应比例系数,β0对应积分系数,β2对应微分系数。引入模糊控制环节可以实时调整控制参数,自动调整到最优的{β0、β1、β2}。

模糊ADRC中的模糊控制器的输入为e1、e2输出为Δβ0、Δβ1、Δβ2,在各自论域中定义7个语言子集为{“负大(NB)”,“负中(NM)”,“负小(NB)”,“零(ZO)”,“正小(PS)”,“正中(PM)”,“正大(PB)”},为减小运算的负载程度,各模糊变量均使用三角隶属度函数。e1、e2的论域选择为[-60,60];Δβ0、Δβ1、Δβ2的论域选取为[-60,60]、[-30,30]、[-6,6]。模糊推理使用Mamdain型,去模糊处理采用加权平均法。建立的模糊规则如表2所示。

表2 Δβ0、Δβ1、Δβ2模糊规则表Table 2 Fuzzy rule table of Δβ0, Δβ1,Δβ2

模糊控制器输出修正系数Δβ0、Δβ1、Δβ2, 根据修正系数以及初始系数即可得到控制参数β0、β1、β2,实现ADRC控制参数自整定。结合非线性摩擦模型中转速与iq的关系,基于摩擦模型前馈补偿的Fuzzy-ADRC结构框图如图9所示。

图9 摩擦前馈补偿模糊ADRC Fig.9 Friction feedforward compensation fuzzy ADRC

基于摩擦前馈补偿模糊ADRC控制器的EMA位置伺服系统如图所示。电流环控制部分仍采用PI控制器,与传统的三环控制策略相比,将位置环和速度环的PI(D)控制器整合为一个复合的Fuzzy-ADRC控制器。使用Fuzzy-ADRC不仅可以提高系统的抗干扰能力与控制精度,也可提高系统的自适应能力。另外该系统也可以做速度环控制,将TD输入信号改为目标速度,将ESO的输入信号改为测量速度,调整模糊ADRC的控制参数,即可实现速度模式控制。基于非线性摩擦前馈补偿的EMA Fuzzy-ADRC控制框图如图10所示。

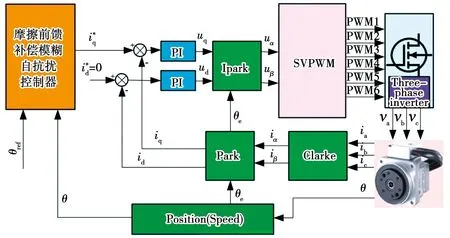
图10 摩擦前馈补偿EMA模糊ADRC控制框图Fig.10 Block diagram of friction feedforward compensation EMA fuzzy ADRC

5 实验分析

为验证基于摩擦前馈补偿模糊ADRC控制器性能,本文在RT-Cube平台进行实验验证。通过空载和加载试验对比分析PI控制、PI-摩擦前馈补偿控制、ADRC控制、ADRC-摩擦前馈补偿、Fuzzy-ADRC-摩擦前馈补偿5种控制方式的特性。

试验平台如图11所示。EMA输入端和输出端均安装有高分辨率增量编码器。

图11 EMA摩擦补偿实验平台Fig.11 EMA friction compensation experimental platform

通过在转盘上吊配重块的形式施加负载,这种静加载方式相比磁粉制动器、扭矩电机具有稳定、准确的优点。实验过程主要数据如表3所示。

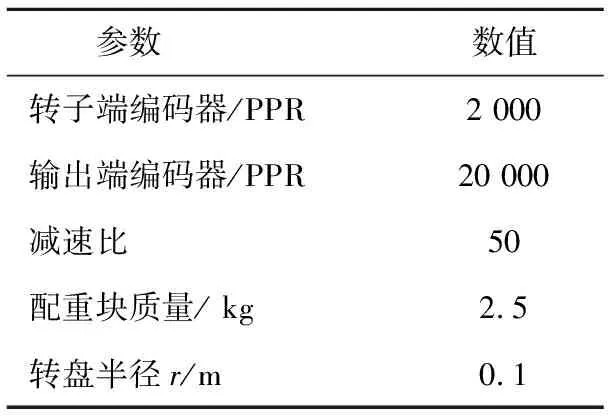
表3 主要参数列表Table 3 List of main parameters

5.1 空载实验分析

EMA输入端、输出端编码器四倍频后可达8 000 PPR和80 000 PPR。给定正弦位置变化信号Pref=8 000sin(πt),目标信号的幅值为EMA输入端编码器的脉冲值。根据谐波减速器减速比和输出端编码器的分辨率可知,EMA输出端位置变化为Pout=1 600sin(πt),输出信号的幅值为输出端编码器的脉冲值。

图12为空载时,给定参考位置信号下,EMA输出端速度变化曲线。从图中看出,EMA中柔轮的转速接近±4 r/min。结合图5可知,该转速跨越了Stribeck速度,包含了摩擦模型中的负斜率段和部分正斜率段。

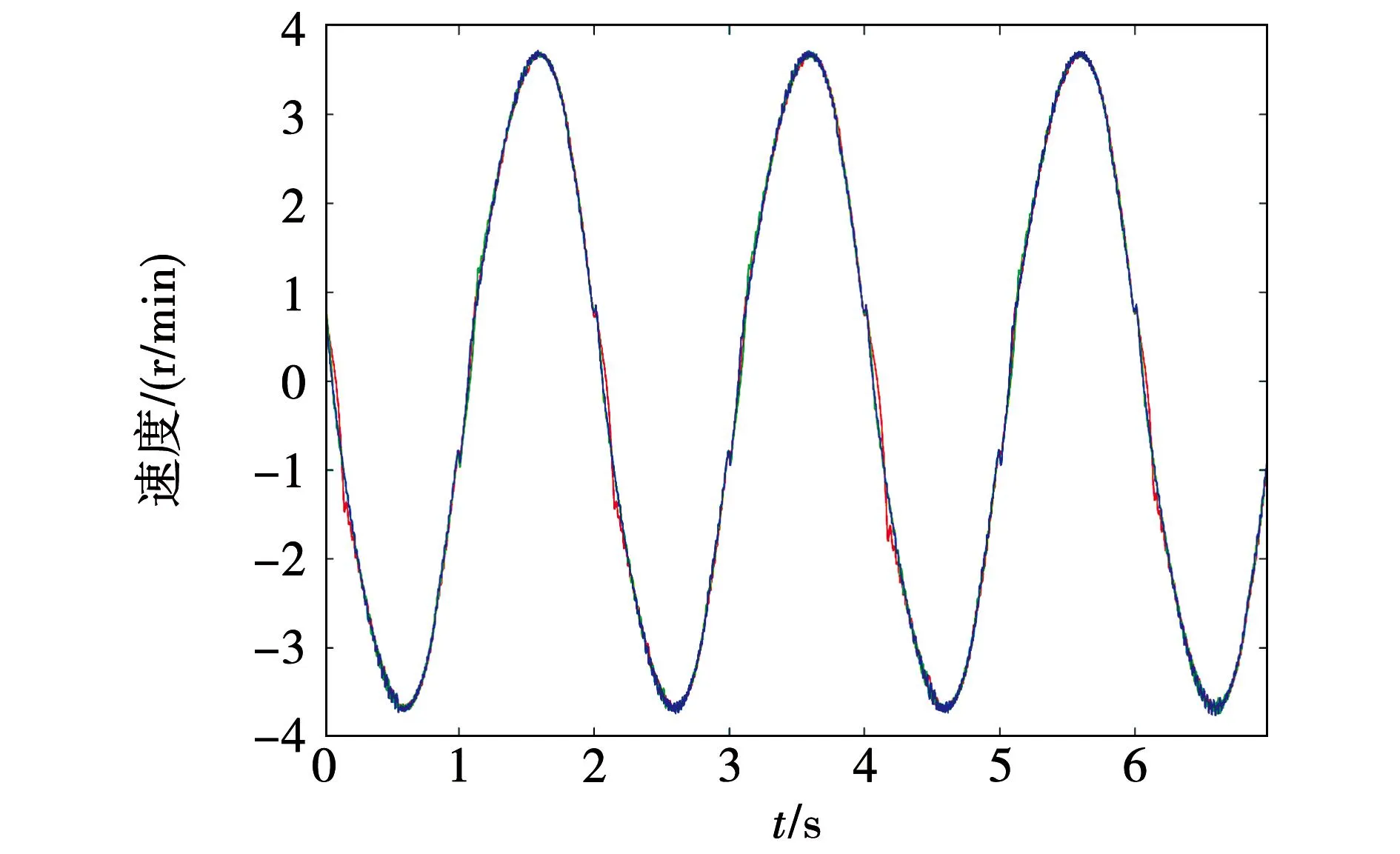
图12 EMA输出端速度Fig.12 EMA output speed

图13为空载时,给定参考位置信号下,EMA输出端位置变化曲线。从图中看出,在到达正弦信号极值点时,PI控制方式误差较大。

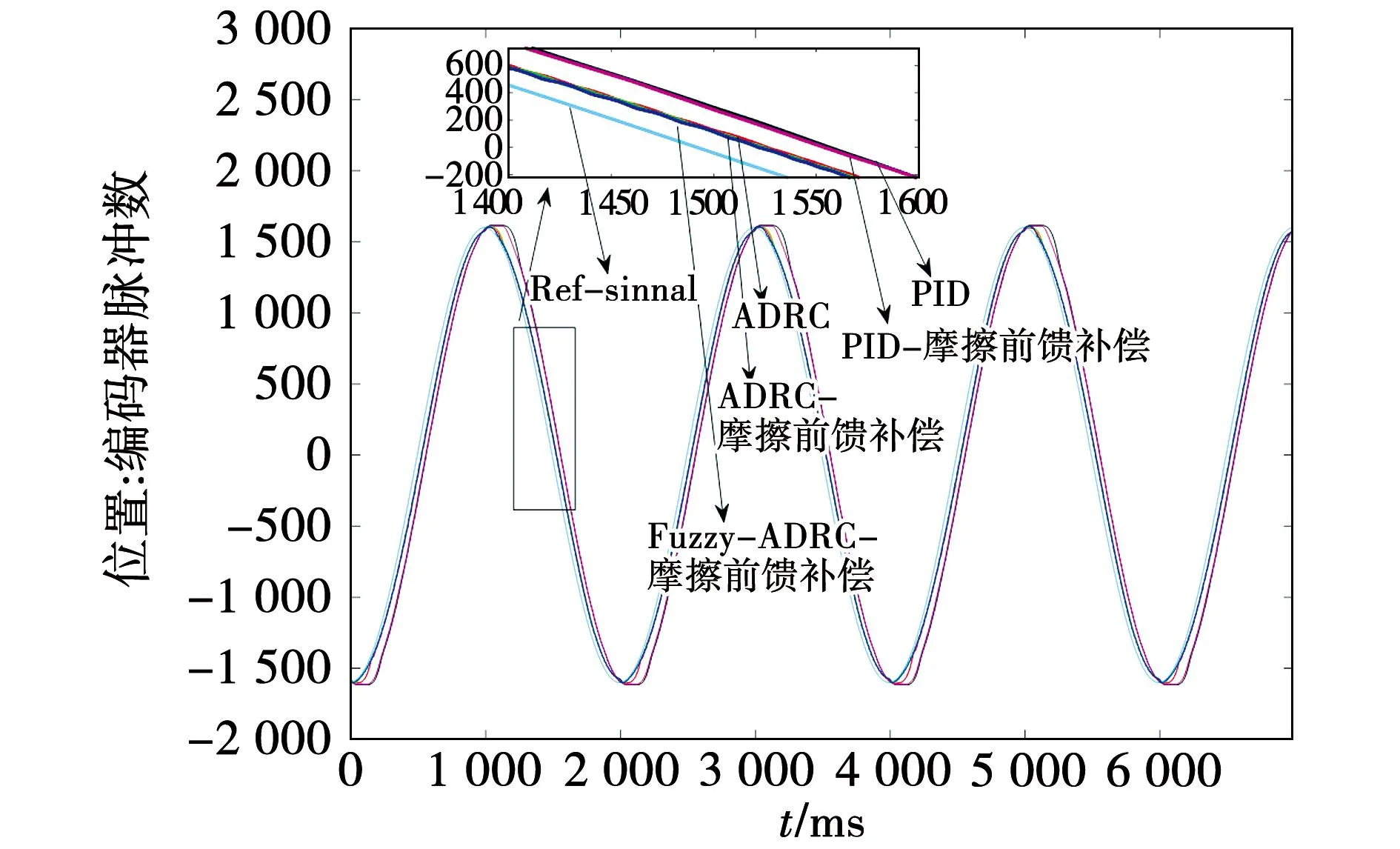
图13 空载EMA输出端位置变化曲线Fig.13 Position change curve of no-load EMA output

图14是位置变化过程中,不同控制方式的实际输出位置与理论输出位置的误差变化曲线。

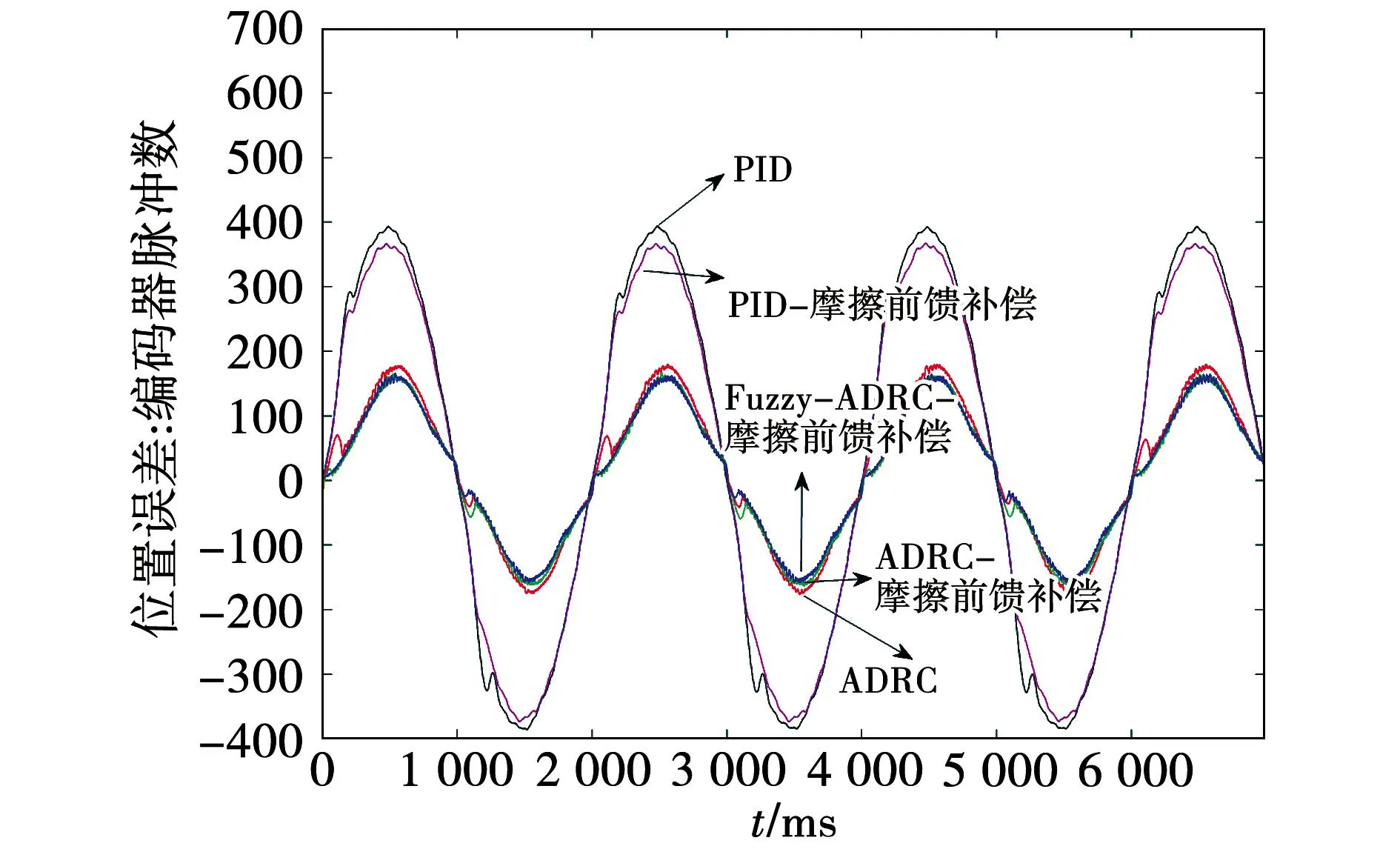
图14 空载EMA输出端位置误差变化曲线Fig.14 Change curve of position error of no-load EMA output

通过峰-峰值,均方根误差作为评价指标,对比分析5种控制方式性能,确定摩擦前馈补偿对位置控制精度的影响。均方根误差表达式为

(19)

5种控制方式的均方根误差和峰-峰值计算结果如表4所示。

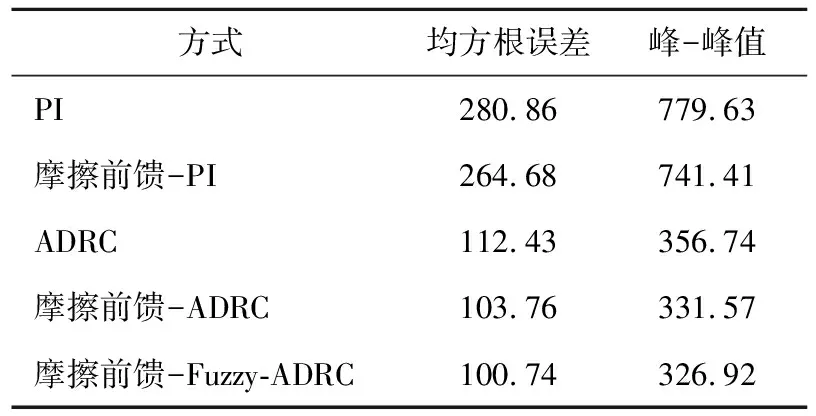
表4 空载实验结果Table 4 No-load test results

从图14能够得出空载时,ADRC控制方式的精度优于PI控制精度。表4中,加入摩擦前馈补偿后,PI和ADRC这两种控制方式的位置误差均方根值和峰-峰值均有所改善。摩擦前馈-PI较PI的均方根误差提高了约16,摩擦前馈的Fuzzy-ADRC较ADRC提高了约12。摩擦前馈Fuzzy-ADRC较PI的均方根误差减小约180,峰-峰值减小约453。

5.2 负载实验分析

负载实验时向转盘挂载2.5 kg配重块,转盘半径为0.1 m,即向EMA施加2.5 N·m负载。图15为负载时,不同控制方式的实际输出位置与理论输出位置的误差变化曲线。

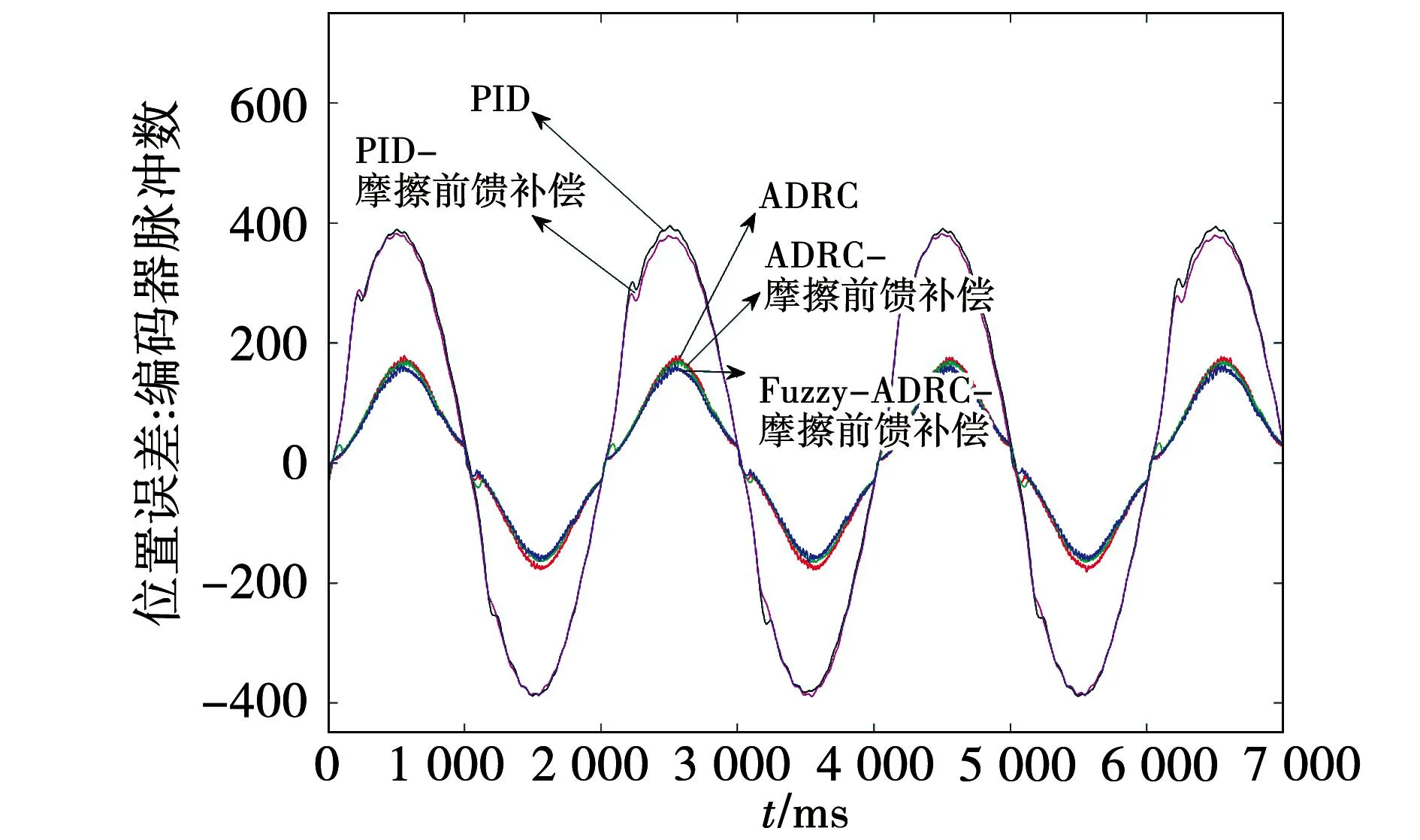
图15 负载EMA输出端位置误差变化曲线Fig.15 Change curve of position error of load EMA output

负载时,5种控制方式的均方根误差和峰-峰值计算结果如表5所示。

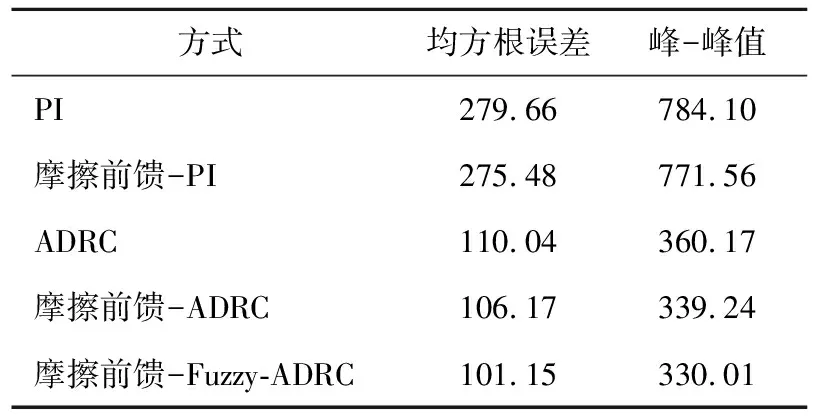
表5 负载实验结果Table 5 Load test results

从图15和表5中能够得出负载时,ADRC控制方式的精度优于PI控制精度。加入摩擦前馈补偿后,位置误差的均方根值和峰-峰值均有所改善。摩擦前馈-PI控制方式的峰-峰值较PI控制方式的峰-峰值减少约13,摩擦前馈-Fuzzy-ADRC的峰-峰值较ADRC的峰-峰值减少约30。摩擦前馈Fuzzy-ADRC较PI的均方根误差减小约180,峰-峰值减小约454。

图16为位置跟踪过程中NLSEF中修正系数Δβ0、Δβ1、Δβ2的变化情况。

图16 β0、β1、β2 变化曲线Fig.16 β0,β1,β2 change curve

从图16中能够看出EMA过程中Fuzzy-ADRC中NLSEF参数在不断的修正,Fuzzy-ADRC可以根据当前工况实时修正控制参数,实现自适应控制,提高系统的控制精度。

6 结 论

本文针对带有谐波减速器的EMA存在的非线性摩擦影响位置控制精度的问题,进行了摩擦前馈补偿以及Fuzzy-ADRC控制方法的研究。几种控制方式中,PI控制方式具有结构简单、参数物理意义明确、容易实现的优点,但存在超调,抗扰动能力弱的缺点。ADRC具有较强的抗扰动力和较快的跟踪速度,但存在结构复杂,控制参数不易整定的问题。Fuzzy-ADRC可以根据实际工况实现ADRC中部分参数的自适应功能。研究了PMSM模型和谐波减速器模型,推导了摩擦力矩与iq的数学关系。使用卡尔曼滤波+小波去噪的方法对测试数据进行处理,获取了不同转速下可靠的iq值。设计了EMA速度/位置复合型的Fuzzy-ADRC控制器,给出了NLSEF中控制参数的模糊规则表。根据库伦+粘滞+Stribeck模型描述力矩与iq关系,结合ESO输出的变量,设计了摩擦前馈补偿的Fuzzy-ADRC。最后在RT-Cube平台,针对PI、摩擦前馈补偿-PI、ADRC、摩擦前馈补偿-ADRC、摩擦前馈补偿-Fuzzy-ADRC 5种控制方式进行正弦位置跟踪实验。实验结果表明,无论负载和空载状况下,ADRC的控制精度优于PI的控制精度,加入摩擦前馈补偿之后,PI和ADRC均可以有效地减弱非线性摩擦引起的位置误差,这5种控制方式中摩擦前馈补偿的Fuzzy-ADRC控制精度最优。加入摩擦补偿环节,使用Fuzzy-ADRC对提高EMA位置伺服精度具有重要意义。