基于复系数滑模观测器的永磁同步电机位置估计误差抑制
胡勤丰, 张芮嘉
(南京航空航天大学 自动化学院,江苏 南京 211106)
0 引 言
永磁同步电机(permanent magnet synchromous motor,PMSM)因具有效率高、功率密度大、结构简单、易于维护等特点,被广泛应用于工业控制、航空航天、交通运输以及家用电器等领域[1-2]。众所周知,转子位置的精度直接影响PMSM矢量控制的性能,为了得到转子的精确位置通常在电机转子侧同轴安装位置传感器。然而采用位置传感器会带来体积增大、成本增加、可靠性降低等问题,尤其限制了其在恶劣环境下的应用,因此无位置传感器控制已成为近年来的研究热点[3]。
目前PMSM的无位置传感器控制方法可以根据适用转速范围分为两类。第一类是基于电机凸极特性的高频注入法,该方法适合零低速运行阶段,主要包括旋转高频注入法[4]、脉振高频注入法[5]、高频方波注入法[6]等;第二类是基于反电动势或磁链的模型法,该方法适合中高速运行阶段,主要包括磁链估计法[7]、模型参考自适应算法[8-9]、滑模观测器(sliding mode observer,SMO)法、扩展卡尔曼滤波器法[10]等。在中高速区,基于滑模观测器的位置估计方法因具有结构简单、易于实现、对电机参数鲁棒性强的优势,得到了广泛的应用[11-12]。
基于滑模观测器的位置估计误差可分为谐波误差和稳态误差。其中谐波误差一方面是由滑模观测器变结构特性所引起的估计反电动势抖振导致的[13],另一方面是由磁链空间谐波、逆变器非线性[14]、电流采样误差[15]等因素导致的。谐波误差引起的矢量控制坐标变换不准确会导致dq轴电流脉动和转矩脉动。为了改善滑模观测器引起的抖振问题,通常采用sigmoid函数代替sign函数,文献[16]分析了sigmoid函数的平滑特性,有效改善了滑模观测器引起的抖振问题。在滑模观测器趋近率方面,文献[17]提出一种新型非线性趋近率并应用于永磁同步电机滑模速度控制,该趋近率可以动态地适应滑模面和系统状态的变化,保持滑模控制器动态性能的同时有效抑制抖振。文献[18-19]分别将超螺旋二阶滑模和分数阶滑模应用于永磁同步电机与感应电机的无位置传感器控制系统中,可以有效削弱抖振,且不影响观测器鲁棒性。为了提高谐波抑制能力,文献[20]提出了一种基于饱和函数的误差电压补偿方法,减小了由逆变器非线性导致的位置估计误差脉动。文献[21]提出了一种带自适应陷波滤波器的锁相环,能够有效抑制估计位置中的六次谐波误差。文献[22]将同步频率提取滤波器引入位置估计,并结合锁频环实现频率跟踪自适应,有效滤除了噪声与各次谐波。
如上所述,位置估计谐波误差有了很大的改善,但对于位置估计稳态误差的研究仍然不充分。位置估计稳态误差会使系统偏离最大转矩电流比状态,降低系统带载能力,因此对该稳态误差进行抑制是十分必要的。滑模观测器的位置估计稳态误差一方面由电机参数偏差导致,另一方面由低通滤波器、采样延时等非理想环节导致。电机参数偏差在低转速大负载时对估计位置的影响较为突出,文献[23]采用递推最小二乘法进行参数辨识,将辨识出的参数应用于观测器中,提高了位置估计的准确性。文献[24]提出一种双重锁相环,对电流信号进行延迟重构,有效补偿了上述非理想环节造成的位置误差。文献[25]提出一种自适应基准锁相环,能够同时补偿电机参数偏差以及上述非理想环节导致的位置误差,但动态性能有待提升。目前,sigmoid函数已经成为滑模观测器中的常用开关函数。采用sigmoid函数能够有效抑制估计反电动势的抖振,虽然可以取消低通滤波器[16,26],却仍然会引起估计反电动势滞后的问题,进而产生额外的位置估计稳态误差。文献[27]对此展开了分析,提出了基于位置估计误差表达式的直接补偿方法,提高了位置估计精度。然而该方法仅是对估计反电动势滞后引起的位置误差进行直接补偿,没有从根本上解决反电动势滞后的问题,并且计算周期较长。
针对上述问题,本文在分析采用sigmoid函数的传统滑模观测器位置估计误差产生机理的基础上,提出一种复系数滑模观测器(complex coefficient sliding mode observer,CC-SMO)。利用两相静止坐标系的相位关系在传统滑模观测器中引入复系数电流误差项,解决估计反电动势相位滞后的缺陷,实现转子位置的精确估计,提高无位置传感器系统控制性能。最后基于一台表贴式永磁同步电机进行实验,验证所提出算法的有效性。
1 传统滑模观测器原理
基于SMO和锁相环(phase-locked loop,PLL)的PMSM无位置传感器控制系统框图如图1所示。其中,SMO根据电压和电流对反电动势进行估计,PLL用来跟踪转子位置。
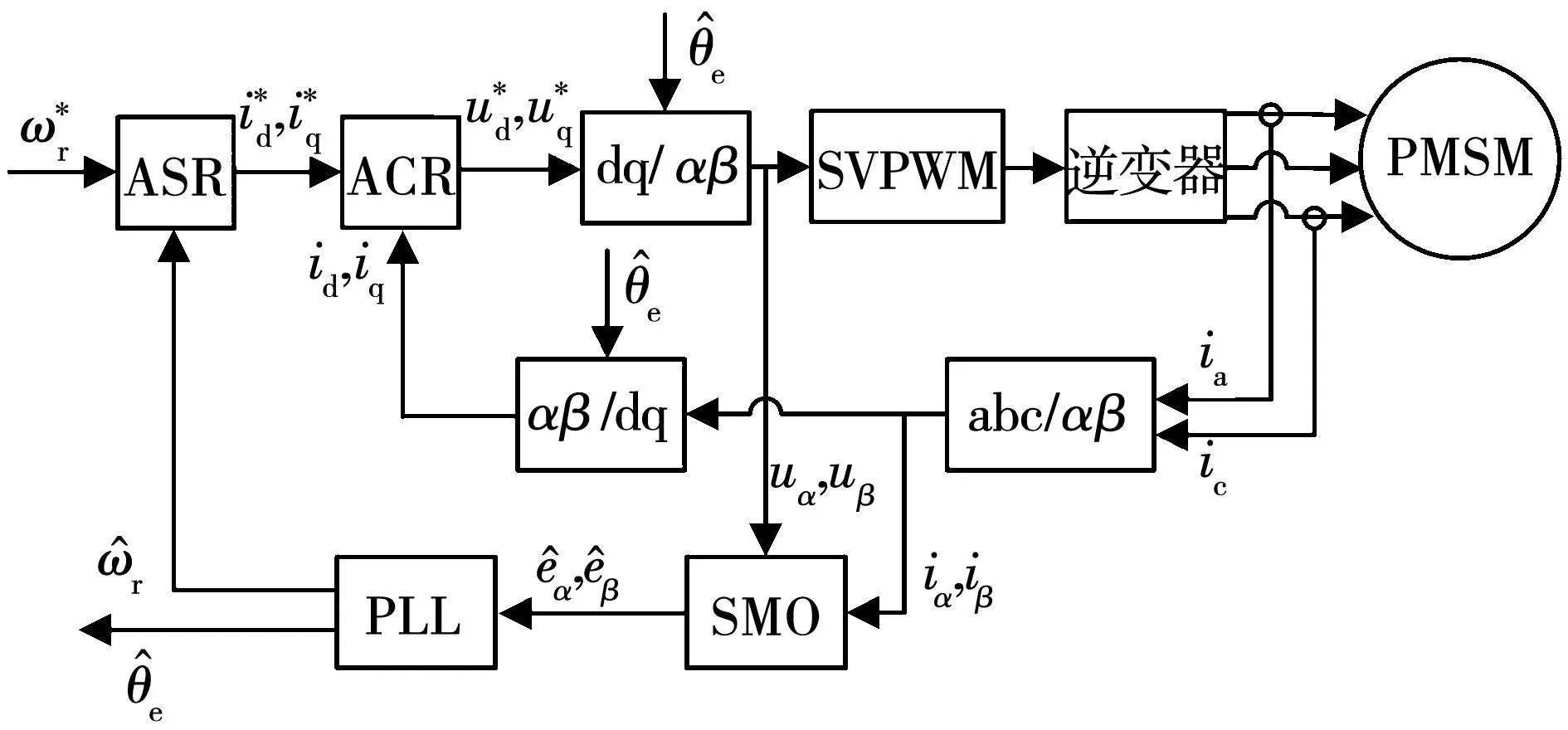
图1 基于SMO的PMSM无位置传感器控制系统框图Fig.1 Diagram of PMSM sensorless control system based on SMO
1.1 表贴式永磁同步电机数学模型
表贴式PMSM在αβ参考坐标系下的数学模型为:
(1)
式中:uα、uβ、iα、iβ和eα、eβ分别表示αβ轴的电压、电流和反电动势;R和L是电机定子绕组的电阻和电感。反电动势eα、eβ的表达式为:
(2)
式中:ψf、ωe和θe分别为永磁体磁链、电角速度和电角度。
1.2 基于传统滑模观测器的反电动势观测
传统滑模观测器方程为:
(3)
式中:符号^表示估计值;Ks为滑模增益。其结构框图如图2所示。

图2 传统SMO结构框图Fig.2 Diagram of traditional SMO
将式(3)和式(1)做差得到电流误差方程为:
(4)
根据式(4)可得PMSM在两相静止坐标系下的估计反电动势:
(5)
2 估计反电动势相位误差分析
sigmoid函数的示意图如图3所示。a为sigmoid函数的斜率系数,δ为sigmoid函数的边界层厚度。当|x|>δ时,sigmoid函数可以等效为sign函数;当|x|≤δ时,sigmoid函数近似于线性函数。因此,将sigmoid函数等效为一个分段函数[28]:
(6)
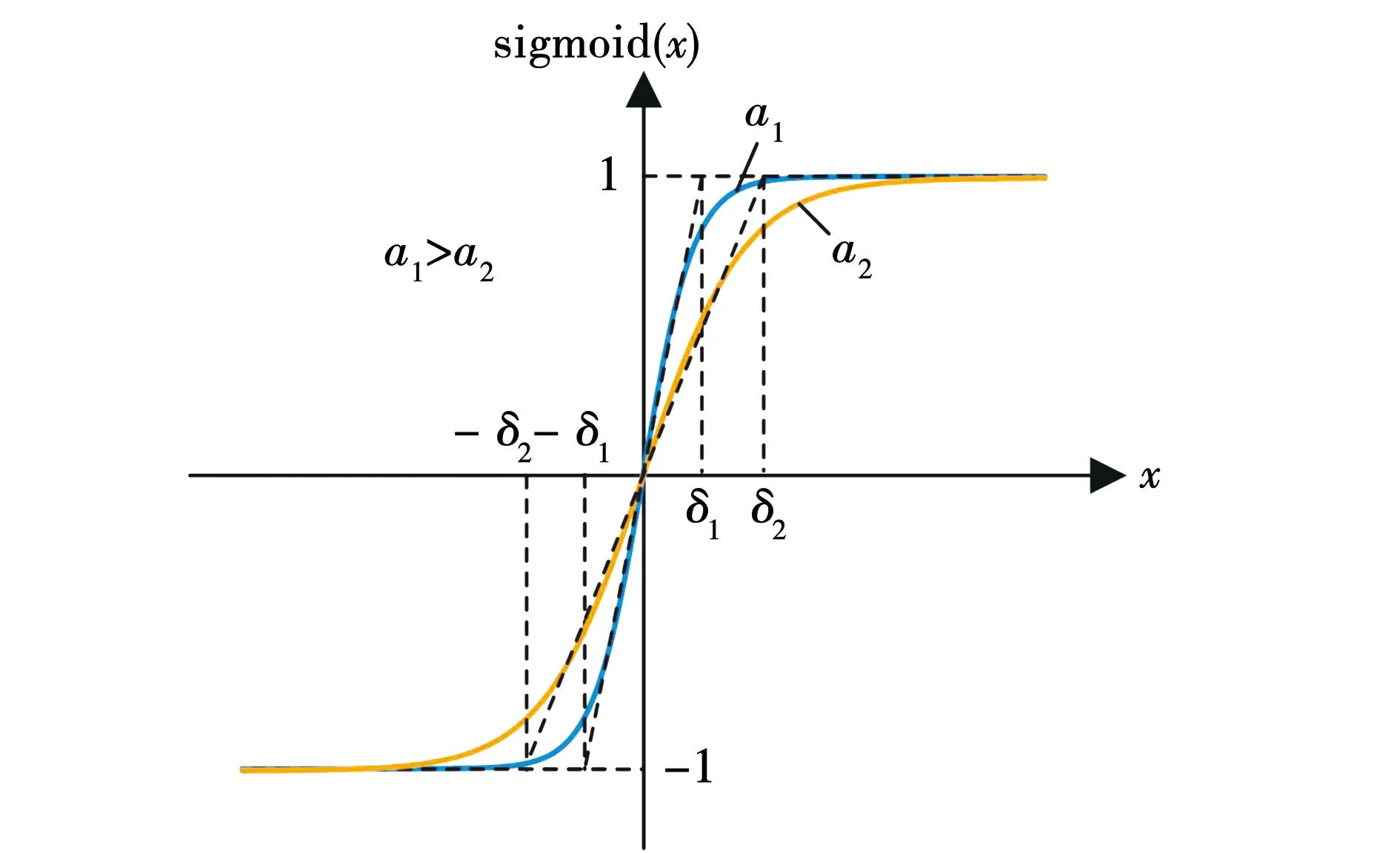
图3 sigmoid函数示意图Fig.3 Schematic diagram of sigmoid function
(7)
(8)
(9)

(10)
(11)
根据式(11)可知,传统滑模观测器的估计反电动势存在幅值衰减和相位滞后。其相位滞后角Δθe为
(12)
在R=0.085 Ω,L=0.121 mH,Ks=49.88条件下,估计反电动势相位滞后角Δθe随转速n和参数a的变化关系如图4所示。可以看出电机转速越高、参数a越小,Δθe越大。一般来说,为了得到较为平滑的估计反电动势波形,需要选择一个较小的a值,然而较小的a值将导致较大的Δθe。过大的Δθe可能导致系统不稳定。

图4 不同转速与参数a下的反电动势相位滞后角Fig.4 Back-EMF phase lag angle under different speed and parameter a
锁相环根据估计反电动势的相位关系跟随转子位置,估计反电动势与实际反电动势存在相位偏差,那么由此计算的转子位置角度必然与实际转子角度存在偏差。因此,保证反电动势无相位差估计对永磁同步电机无位置传感器控制非常重要。
3 复系数滑模观测器设计与分析
3.1 复系数滑模观测器设计
由式(11)可知,传统滑模观测器的估计反电动势表达式中含有一个复数项jωeL。当采用sign函数时,滑模面附近的等效增益为+∞,即a等效为+∞,因此jωeL项造成的相位滞后趋近于0;而sigmoid函数在滑模面附近引入线性控制段,滑模面附近的等效增益a/2为一个有限常数,所以jωeL项将造成不可忽略的估计反电动势相位滞后。因此,估计反电动势表达式中的复数项jωeL是产生相位滞后的根本原因。
基于上述分析,本文在传统滑模观测器中引入估计电流误差的复系数项,构造一种复系数滑模观测器:
(13)
根据iα=jiβ,该复系数电流误差项可以等效为一个电流误差交叉耦合项。复系数滑模观测器的结构框图如图5所示。
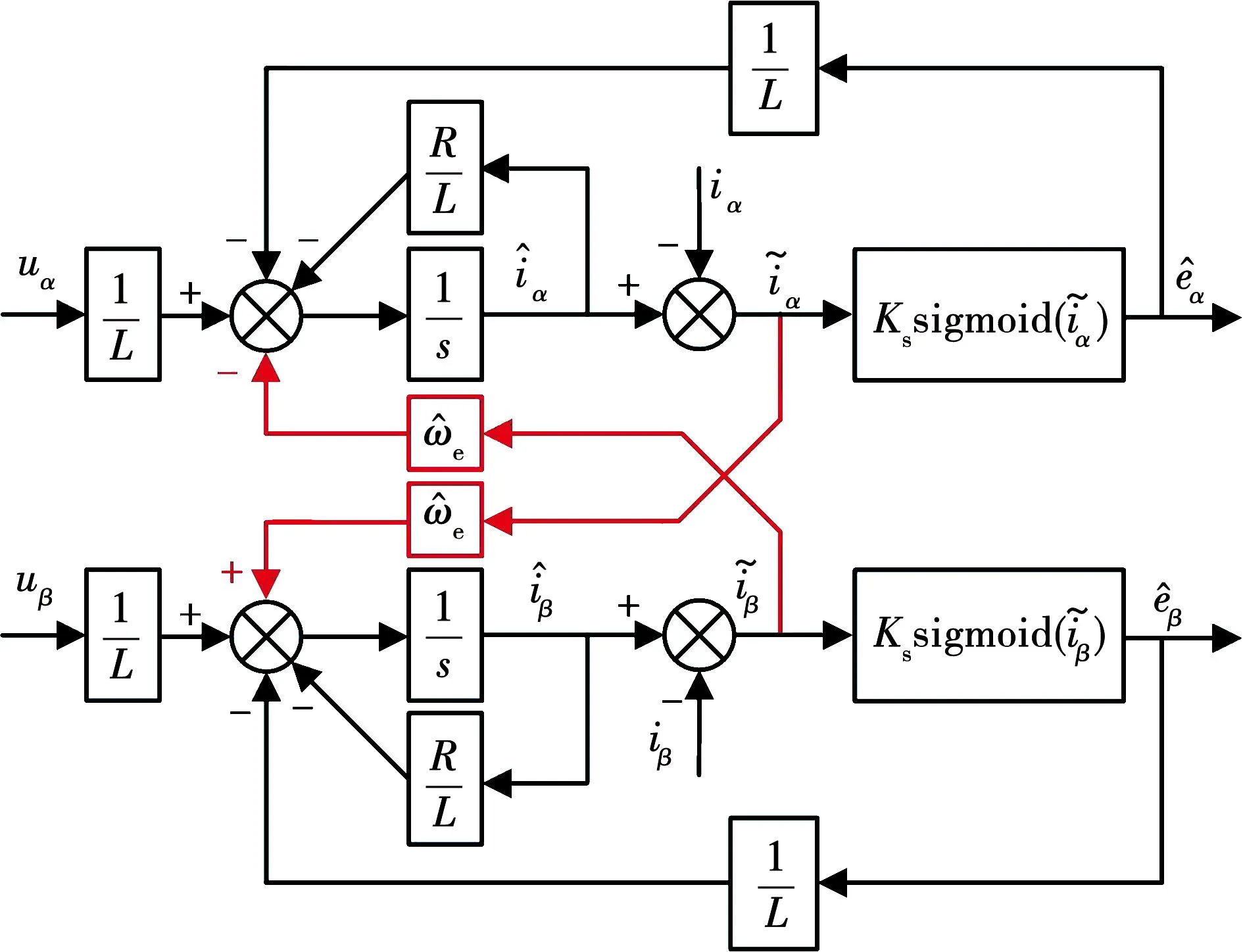
图5 CC-SMO结构框图Fig.5 Diagram of CC-SMO
将式(13)和式(1)做差得到电流的动态误差:
(14)
稳态时,反电动势估计值与式(5)相同。
3.2 复系数滑模观测器的估计反电动势分析
(15)
同理,构造状态变量x2,使x2的平衡点为0,即
(16)
将式(15)代入式(16),其状态方程可以改写为
(17)
(18)
根据式(18),复系数滑模观测器的估计反电动势的表达式中不再包含复数项jωeL,sigmoid函数中的线性段将不再造成估计反电动势相位滞后。

(19)
同理,状态变量x3可构造为
(20)
式(18)可以写为
(21)
此时,复系数滑模观测器得到的估计反电动势既无相位滞后也无幅值衰减,可以实现实际反电动势的精确估计。
3.3 复系数滑模观测器稳定条件分析
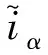
3.4 复系数滑模观测器动态性能分析
滑模观测器的动态性能影响电机在突加突卸负载、突加突减速时的转速波动与稳定时间。滑模观测器的动态性能体现在滑模量的趋近速度,其动态响应过程可以分为两个阶段:非线性段和线性段。
当滑模量在非线性段时,传统滑模观测器与复系数滑模观测器的动态性能均由滑模增益Ks决定,Ks越大趋近速度越快,趋近时间越短,但观测值抖振水平也相应增加。
当滑模量在线性段时,传统滑模观测器的状态方程式(10)的解为
(22)
可见,此时动态性能与a相关,a越大,趋近速度越快。
同理,复系数滑模观测器的状态方程式(17)的解为
(23)
式(23)和式(22)的衰减项时间常数一致。因此,引入复系数项后并没有影响观测器的动态性能。
4 实验验证
为了验证本文提出的复系数滑模观测器的有效性,搭建了基于TMS320F28335的硬件实验平台,开关频率为10 kHz,如图6所示。实验电机是一台880 W/3 000 r·min-1的表贴式PMSM,其具体参数如表1所示。
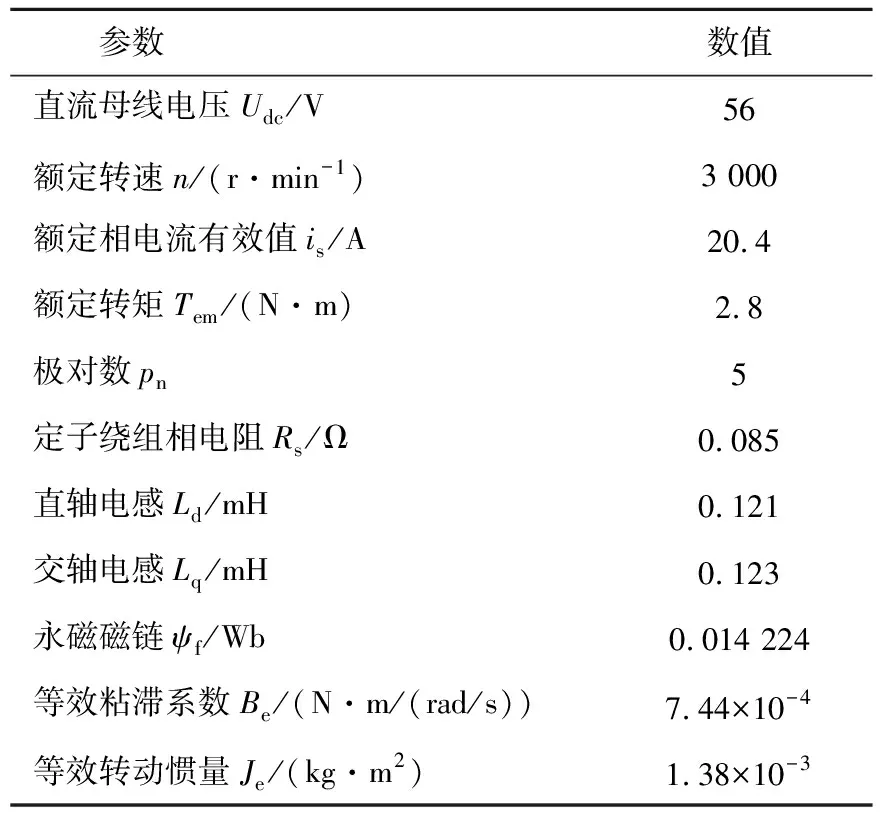
表1 PMSM参数Table 1 PMSM parameters
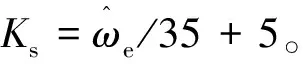
为了验证估计反电动势与实际反电动势的相位、幅值关系,给定电机额定转速,在a值分别为0.09、0.04和0.01三种情况下进行实验。实验结果如图7、图8所示。
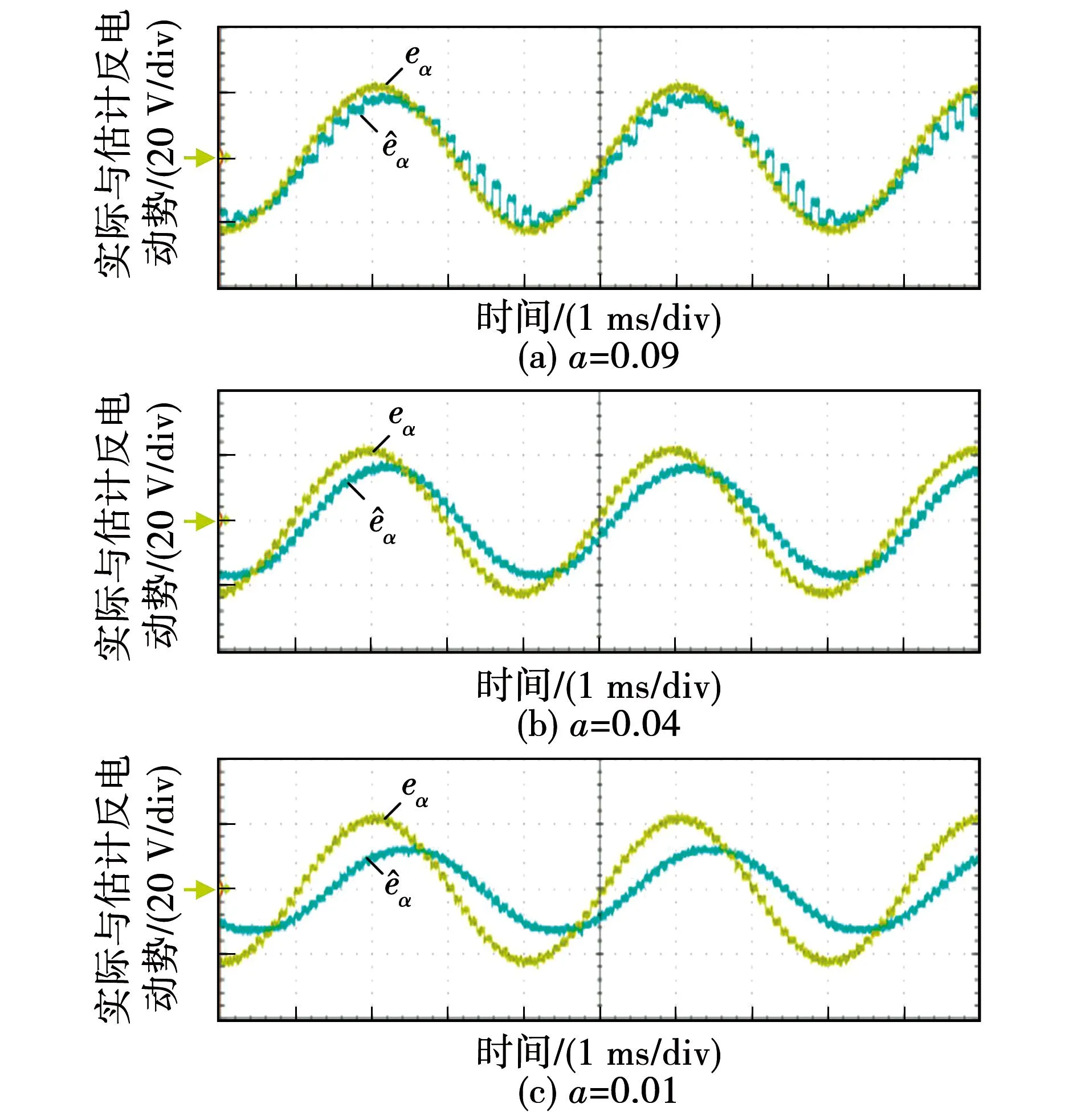
图7 采用传统SMO的反电动势实验结果Fig.7 Experimental results of back-EMF using traditional SMO
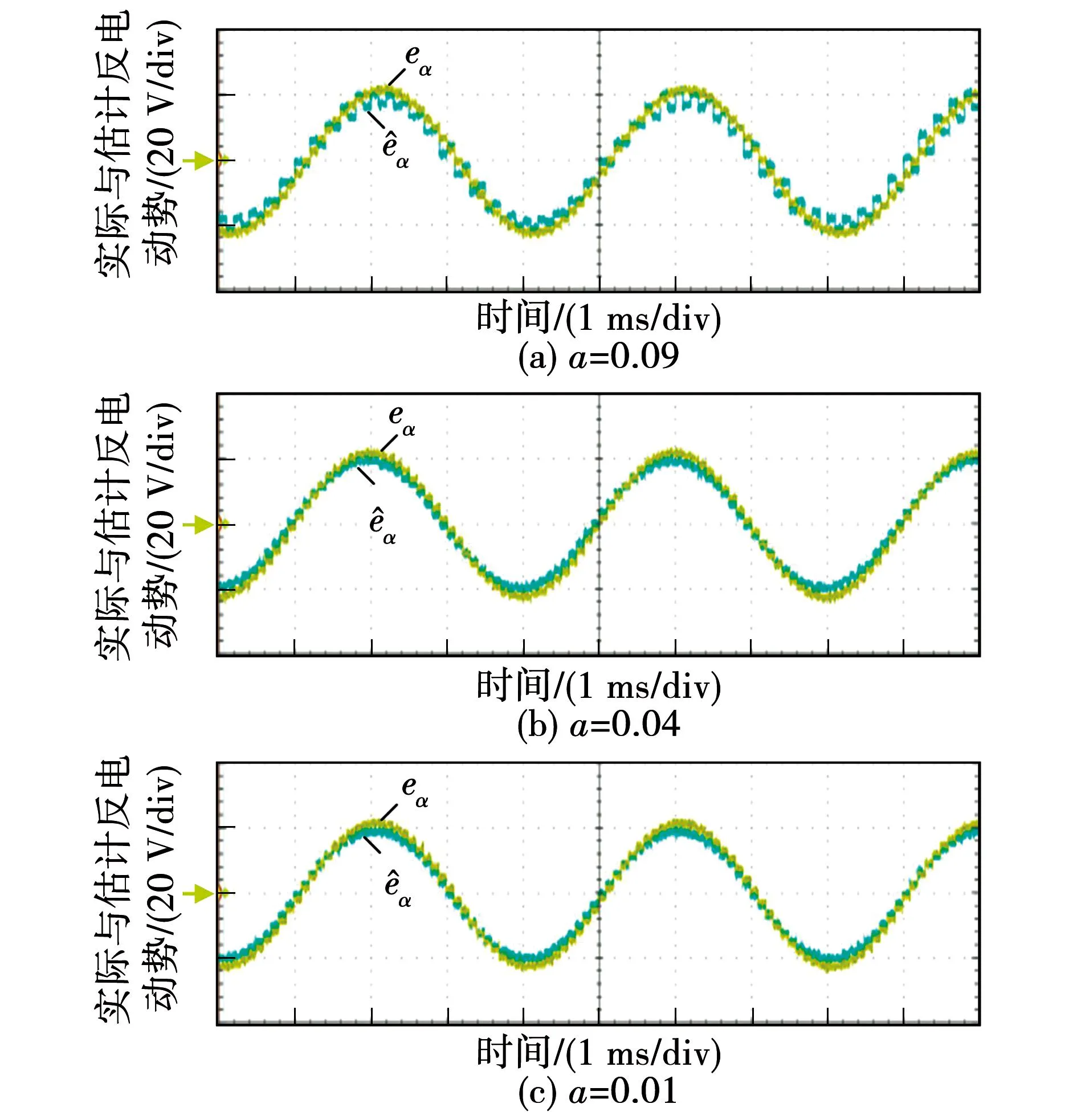
图8 采用CC-SMO的反电动势实验结果Fig.8 Experimental results of back-EMF using CC-SMO
其中,图7为采用传统SMO的实际与估计反电动势实验结果,图8为采用CC-SMO的实际与估计反电动势实验结果。可见a值越小估计反电动势越平滑。采用传统SMO时,估计反电动势存在幅值衰减和相位滞后,且a值越小这一现象越明显。而采用CC-SMO在任意a值下都能实现反电动势的准确观测。
为了验证所提出的CC-SMO在不同a值和不同转速下的位置估计误差抑制效果,在空载工况下对传统SMO和CC-SMO两种算法进行实验。实验结果如图9、图10所示。
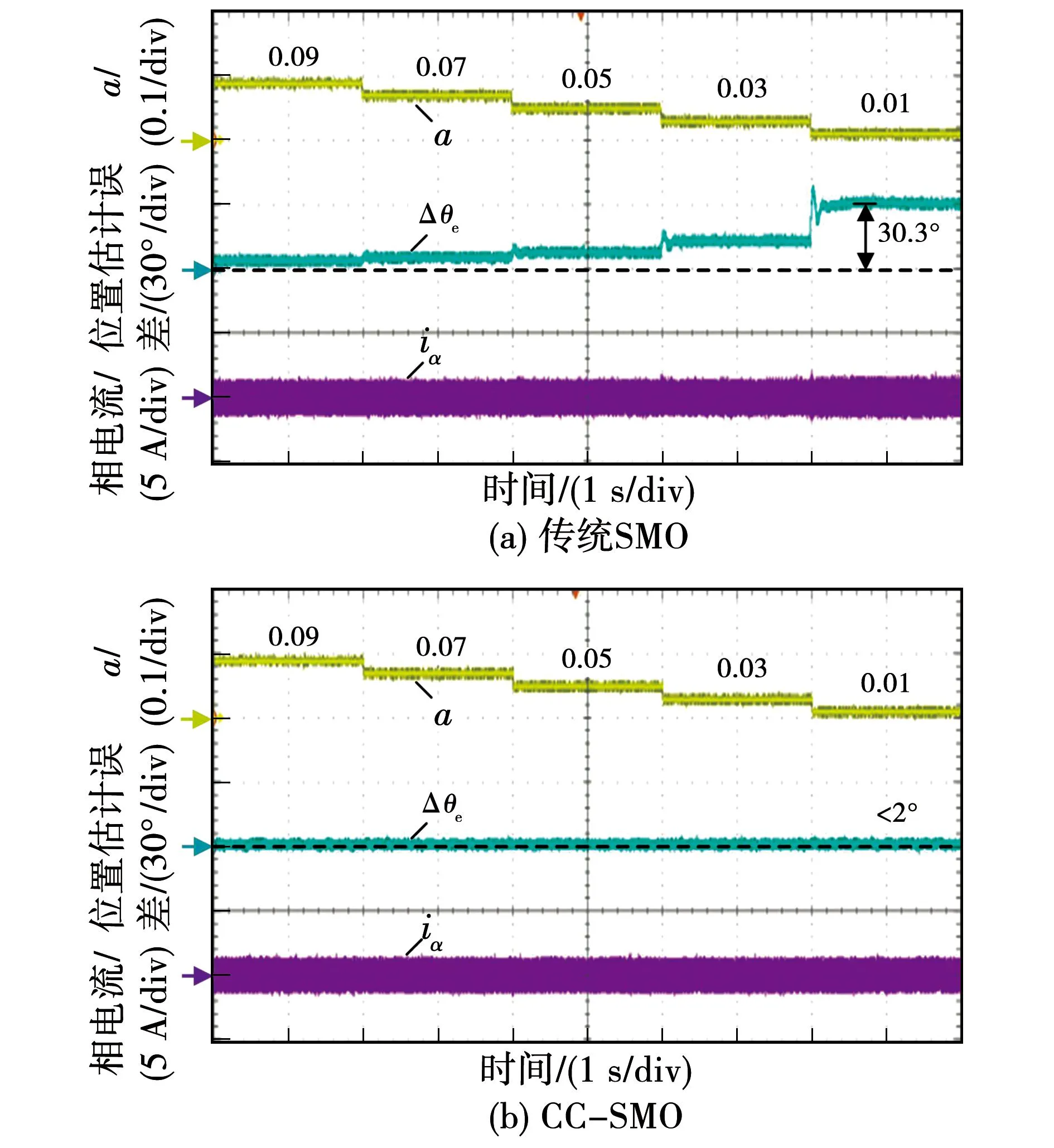
图9 不同a下的空载实验结果Fig.9 Experimental results under different a with no load condition
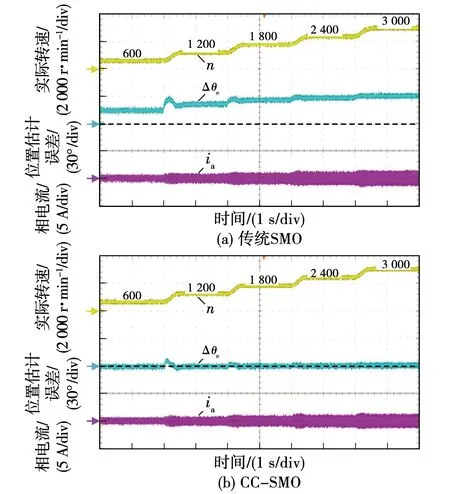
图10 不同转速下的空载实验结果Fig.10 Experimental results under different speeds with no load condition
其中,图9为额定转速下a从0.09逐步减小到0.01的实验结果,a每2 s减小0.02。图10为a给定0.01,转速从600 r/min逐步增加到3 000 r/min(额定转速)的实验结果,转速每2 s斜坡增加600 r/min。由图9(a)和图10(a)可以看出,采用传统SMO时估计位置存在稳态误差,a越小、转速越高,位置估计误差越大。转速为3 000 r/min 、a=0.01时位置估计误差达到30.3°。该实验结果与理论分析一致,验证了对位置估计误差进行抑制的必要性。由图9(b)和图10(b)可见,采用本文提出的CC-SMO算法后,在不同a值与不同转速下估计位置误差均保持在2°电角度以内。该实验结果初步验证了本文提出的CC-SMO算法的有效性。
为了验证所提出的CC-SMO在带载工况下的位置估计误差抑制效果,在50%额定负载工况下对传统SMO和CC-SMO两种算法进行实验。实验结果如图11、图12所示。
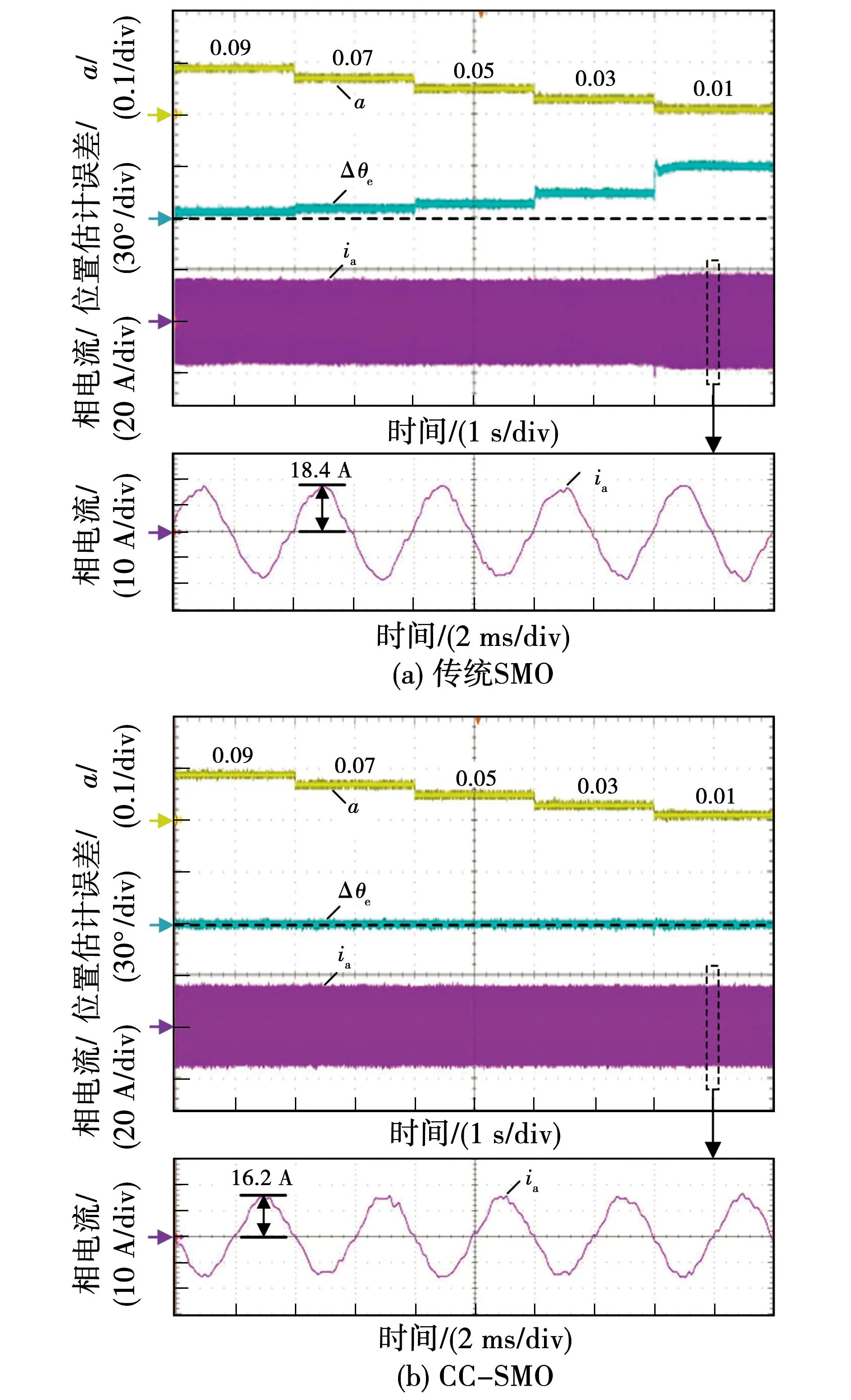
图11 不同a下的带载实验结果Fig.11 Experimental results under different a with load condition
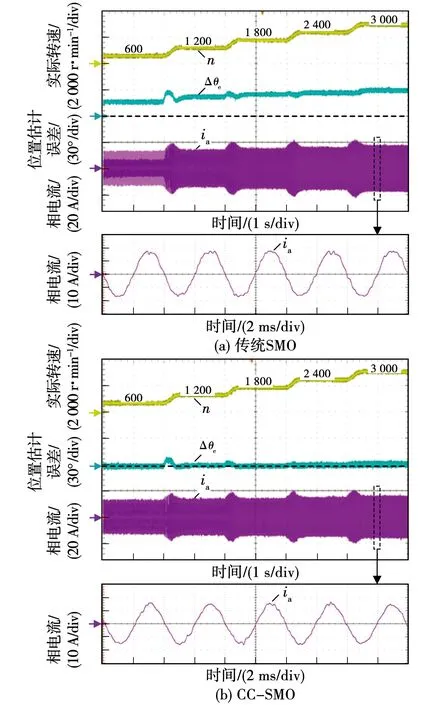
图12 不同转速下的带载实验结果Fig.12 Experimental results at different speeds with load condition
同样的,图11为额定转速下a从0.09逐步减小到0.01的实验结果,a每2 s减小0.02。图12为a给定0.01,转速从600 r/min逐步增加到3 000 r/min(额定转速)的实验结果,转速每2 s斜坡增加600 r/min。可见,在带载工况下采用传统SMO时,随着a值与转速的变化,位置估计稳态误差与空载工况具有相同的变化趋势。在带载工况下采用本文提出的CC-SMO时,仍然具有与空载工况相同的位置估计误差抑制效果。由图11(a)可知采用传统SMO时,随着a减小,位置估计误差增大,相电流幅值也随之增大,a给定0.01时,相电流达到18.4 A。由图11(b)可知采用本文提出的CC-SMO时,在不同a值下位置估计误差依然能够得到有效抑制,相电流幅值基本没有变化,为16.2 A。可见a给定0.01时,采用本文提出的CC-SMO后,相电流幅值减小了11.96%。该实验结果进一步验证了本文提出的CC-SMO算法在带载情况下的有效性。
为了验证所提出的CC-SMO的位置估计误差收敛速度,在a分别为0.09、0.04和0.01三种情况下进行了算法切入实验。CC-SMO算法切入瞬间的实验结果如图13所示。
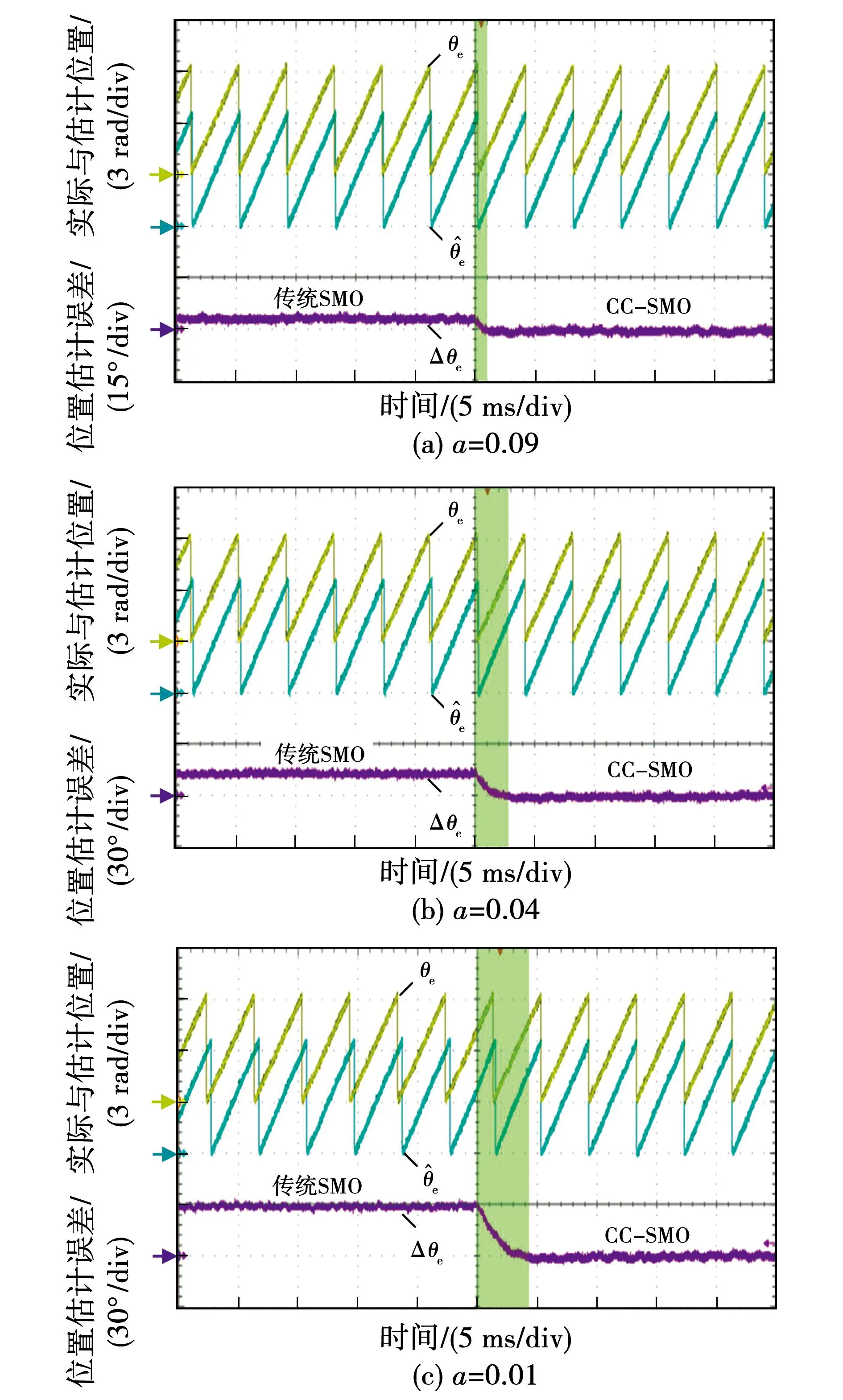
图13 CC-SMO的收敛速度Fig.13 Convergence speed of CC-SMO
由图13可以看出,CC-SMO算法切入前估计位置存在不同程度的相位滞后,而切入CC-SMO算法后,位置估计误差快速收敛至0°附近。a越小、位置估计误差越大,位置估计误差的收敛时间越长,a给定0.01时收敛时间为4.33 ms。该实验结果验证了本文提出的CC-SMO算法在不同a值下均具有良好的收敛速度。
为了验证所提出的CC-SMO在动态工况下的有效性,分别在突变转速与突变负载工况下进行实验。实验结果如图14、图15所示。
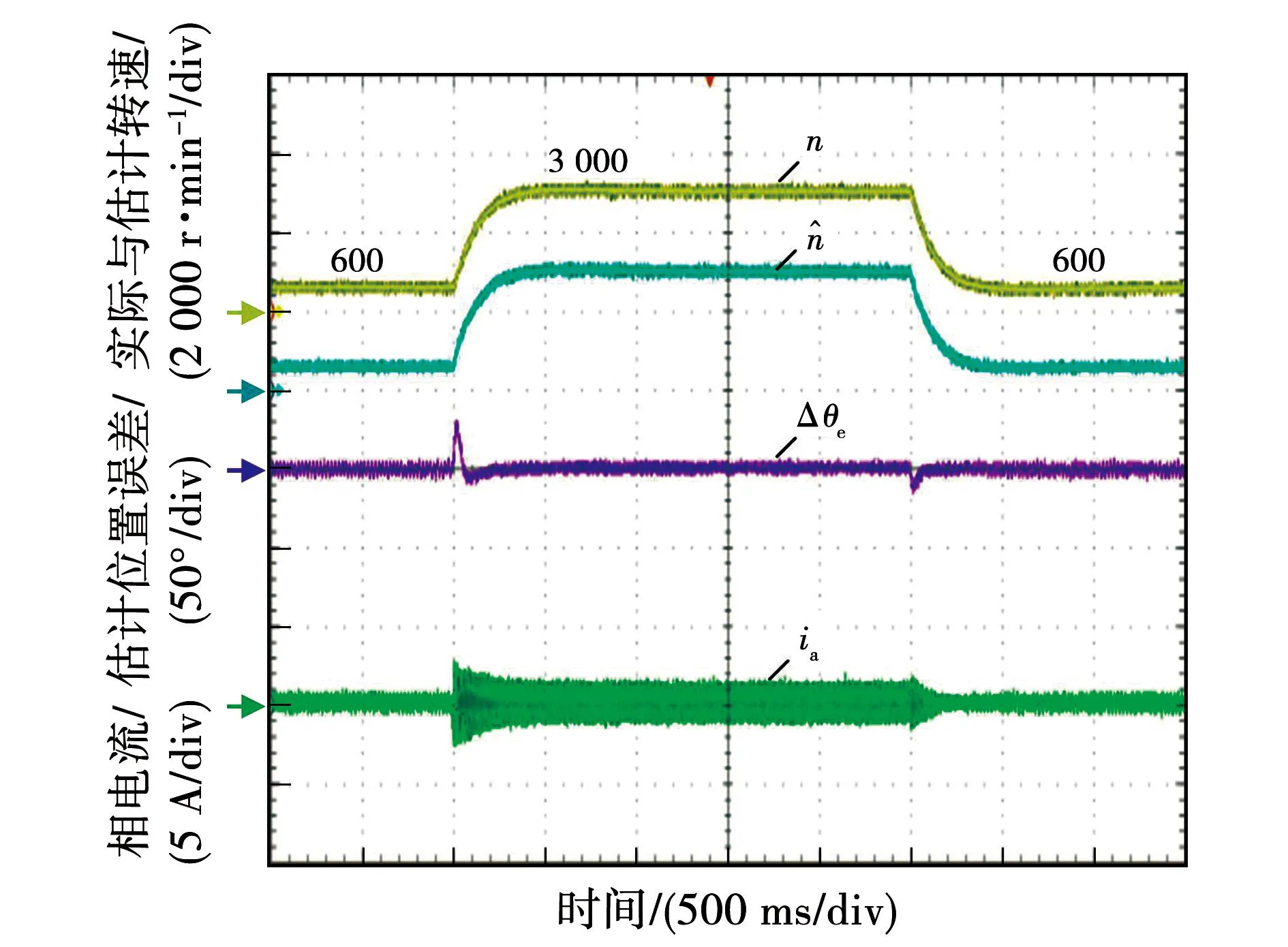
图14 突加突减速动态过程的实验结果Fig.14 Experimental results of dynamic process of sudden acceleration and sudden deceleration

图15 突加突卸载动态过程的实验结果Fig.15 Experimental results of dynamic process of sudden loading and sudden unloading
其中,图14为转速从600 r/min到3 000 r/min(额定转速)再到600 r/min突加突减速动态过程的实验结果。图15给出了额定转速下突加突卸100%额定负载的实验结果。可以看出在突加突减速和突加突卸负载的动态工况下,估计转速能够准确跟踪实际转速,位置估计误差快速收敛至0附近,进一步验证了本文所提出算法在突加突减速与突加突卸负载的动态工况下均具有良好的性能。
为了分析所提出的CC-SMO对运算时间的影响,分别对传统SMO、本文提出的CC-SMO误差抑制方案和根据式(12)的直接补偿方案进行实验测试。由于直接补偿方案涉及反正切运算与除法运算,需要较长的计算周期,而本文提出的CC-SMO仅通过加法与乘法实现。CC-SMO的运算时间与传统SMO相比增加了0.1 μs,而直接补偿方案的运算时间与传统SMO相比增加了1.75 μs,采用CC-SMO与直接补偿方案相比运算时间减少了12.17%。
综上所述,本文进行了较为全面的实验对比,有效验证了对位置估计误差进行抑制的必要性以及本文提出的CC-SMO在不同工况下的有效性。
5 结 论
本文分析了采用sigmoid函数的传统滑模观测器的估计反电动势相位滞后原因,在此基础上构造了一种复系数滑模观测器。通过引入复系数电流误差项,抑制了位置估计误差。根据理论分析和实验结果得出以下结论:
1)传统滑模观测器的相位滞后由估计反电动势表达式中的复数项导致,转速越高、a越小,估计反电动势的相位滞后角越大;
2)复系数滑模观测器能够消除估计反电动势的相位滞后,在不同转速和a值的情况下将位置估计误差抑制到2°电角度以内,提高了转子位置的估计精度,算法收敛时间在5 ms以内,并且没有影响观测器的稳定条件与动态性能;
3)复系数滑模观测器没有引入额外参数、结构简单,与直接补偿方法相比运算时间减少了12.17%。

