机器人关节电机转矩动态特性研究
何伟严, 马吉恩, 王宏涛, 许博文, 方攸同
(1.浙江大学 流体动力基础件与机电系统全国重点实验室,浙江 杭州 310027; 2.浙江大学 电气工程学院,浙江 杭州 310027; 3.浙江大学 交叉力学中心,浙江 杭州 310027)
0 引 言
足式机器人是通过机械腿与地面的接触进行移动的机器人,独特的运动方式使其具有优越的地形适应性和身体姿态灵活性[1-2]。近年来,随着计算机控制技术和关节驱动模组的不断发展,足式机器人的性能不断提升,在安防巡检、救灾探测、军事侦察等领域有了越来越多的应用[1,3]。在足式机器人的各类性能中,高机动性是基础和关键,而奔跑速度是检验机动性的一个常用的指标。许多足式机器人都在追求最高奔跑速度的突破,也取得了不错的结果[4]。
目前的足式机器人大都采用刚性的身体和腿部连杆,通过单一自由度的关节连接起来,由电机或液压装置驱动各关节的运动。为了实现高机动性,机器人的控制系统通常采用带有反馈的分层式控制架构,主要包含运动控制器和关节驱动控制器两部分,前者根据运动指令、环境信息、身体状态反馈给出各关节的角度或力矩指令,后者则控制关节驱动机构产生相应的力矩,实现对前者指令的跟随,实际输出与关节驱动机构本身的特性有关。
在运动控制器的设计问题中,传统的运动控制器通常基于机器人的模型定义为一个轨迹优化问题,而后采用阻抗控制、落足点规划、MPC(model predictive control)[5-9]等方法求解,需要手动调节许多参数。随着深度学习算法的发展,越来越多的研究者采用机器学习方法训练和优化机器人的运动控制器,这种数据驱动的设计方式需要获取大量的机器人运动数据。然而,由于较高的硬件维护成本和安全风险,以及某些数据在实物中较难准确测量(如关节转矩、碰撞点接触力等),研究者们更多地采用动力学仿真而非实验来采集所需数据[10-11]。在这个过程中,模型的准确度和复杂度构成了矛盾,准确度不足会直接影响训练出的运动控制器的可迁移性,而过高的复杂度则会增加仿真时间,使运动控制器的训练变得困难。
目前仿真中训练控制器在迁移到实物机器人的过程中,存在的一个问题是缺少对关节电机本身特性的关注,一般对满足力矩和功率需求范围的关节电机即认为其能够实现指令跟随,这种假设是机器人运动从仿真迁移到实物上时表现出差异的原因之一。同时为了提高控制器的可迁移性,研究者们通常采用两种方法来减小关节电机特性的影响:一是在仿真中对关节电机的力矩输出增加一些噪音或以增加运动控制器的鲁棒性;二是通过建模或数据驱动等方式获得关节驱动器的输出特性,在设计控制器时将其包含到计算机仿真中[12-13]。
前者的方法虽然能在一定程度上提升机器人运动控制的稳健性,但由于添加的随机噪声并不反映关节驱动器工作的实际特征,因此在关节驱动器的转矩输出响应性能方面并不会带来提升;后者的方法获得的关节驱动器输出特性可以明确关节驱动器的存在的饱和、延迟、滞回等不同输出特性,但通常由于关节驱动器的部件较多、模型复杂,现有的研究缺少关节驱动器输出特性的主要决定性参数以及不同的特性对机器人运动的影响机制的讨论。
针对采用电机驱动方式的足式机器人,本文建立电机动态特性+机器人动力学的联合仿真系统。对于系统计算时间长的问题,通过对电机控制器的设计和电机动态特性的分析,得到与电机动态特性基本一致的简化电机特性,并以单关节摆动为例分析参数对电机动态特性的影响。通过对比联合仿真系统中包含和不包含简化的电机动态特性的仿真结果对比,研究电机动态特性对四足机器人高速奔跑时关节转矩、速度的影响,表明高速下电机转矩输出的限制是造成腿部在摆动相中关节速度出现差异的主要原因。
1 联合仿真系统和运动工况分析
本文研究的四足机器人包含身体和4条完全一样的机械腿,腿部包含外展(abduction/adduction,ab/ad)、髋(hip)和膝(knee)3个关节,全身12个关节均采用相同的关节电机模组作为动力来源。关节电机模组采用的是高转矩密度电机和低减速比减速器构成的伪直驱式驱动方案[14]。由于关节电机模组采用了小减速比Gr=6,减速器部分的摩擦阻力相对于电机产生的转矩很小,因而忽略减速器的摩擦转矩,将电机转矩的6倍、电机转速的1/6作为电机模组的输出,以下讨论均针对电机本身。
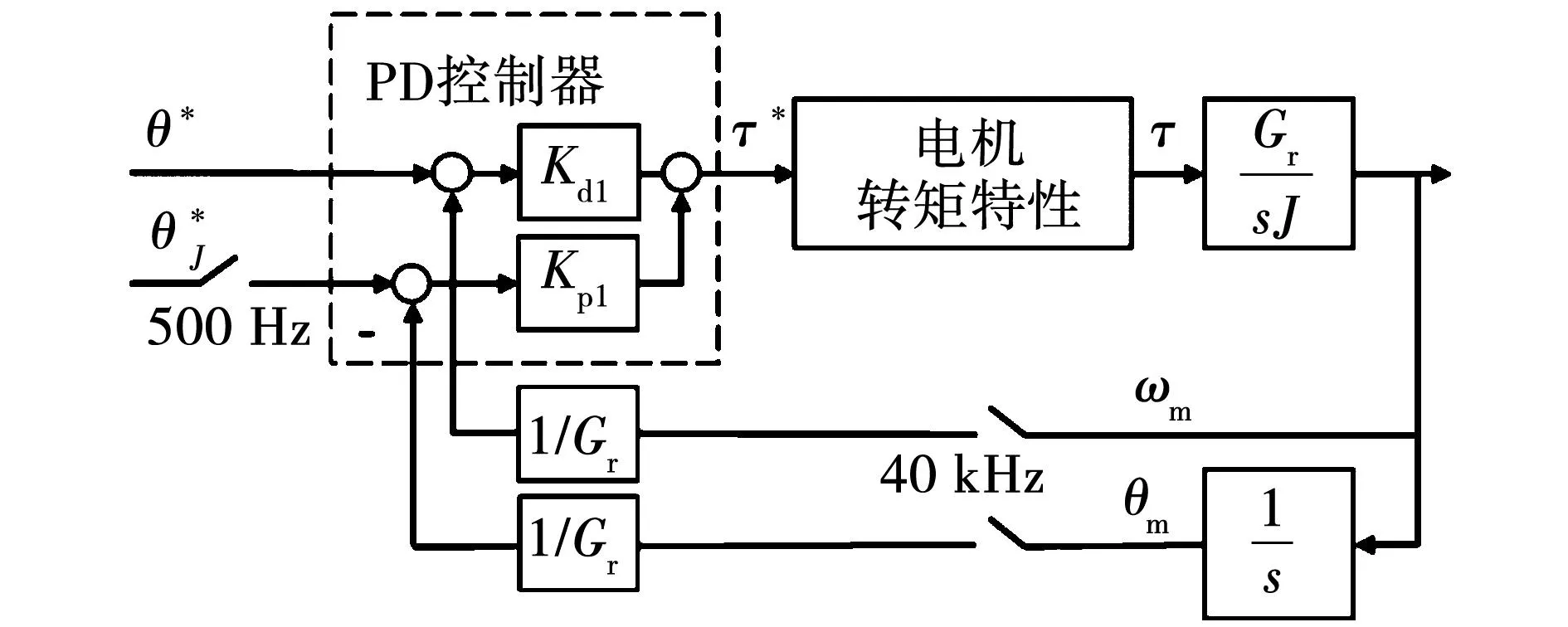
为了研究关节电机转矩输出对采用电驱动四足机器人高速奔跑的影响机制,本文依照实际的机器人控制架构(包含运动控制器和关节驱动控制器)建立电机动态特性+机器人动力学的联合仿真系统,以便于分析机器人高速奔跑工况下电机转矩输出特性对关节转矩、速度、角度的影响。联合仿真系统整体架构如图1所示。

图1 控制架构及仿真平台示意图Fig.1 Schematic diagram of control architecture and simulation platform
其中运动控制器包含LSTM网络和PD控制器。LSTM网络将四肢相位t、速度指令v*、身体的姿态角θb和身体姿态角速度ωb、关节的角度θm和角速度ωm映射为12个关节的参考角度θ*,控制频率为500 Hz。PD控制器将参考角度θ*转化为转矩指令值τ*,即
(1)
其中:θ*的更新频率为500 Hz;θm、ωm和τ*更新频率都为40 kHz。
图1右侧的电机动力学模型和电机控制器两部分共同决定了电机动态特性(假设逆变器能够产生与指令值一致的实际控制电压)。电机动力学模型(即电机实际转矩τ在控制电压u和角速度ωm作用下的变化)由电机本身的类型和测试获得的参数决定。电机控制器按实际控制方法和参数设置,接收转矩指令值τ*并根据电机状态给出控制电压指令值u*。而后u*通过逆变器输出控制电压u,以实现转矩实际值τ对转矩指令值τ*的跟踪。
图1中两个阴影框部分表示本文使用Raisim[15]和Simulink两个仿真平台分别进行机器人动力学和电机动态特性的计算。二者之间的交互通过缓存的数组实现。Raisim在运行时将τ*、θm、ωm缓存,而后将调用Simulink将其加载进来,根据τ*、θm、ωm计算出此时的转矩实际值τ后也缓存在工作区。Raisim加载τ数据后依据描述机器人运动状态的刚体动力学模型和机器人与地面的接触模型等,计算出机器人下一时刻的运动状态θb、ωb、θm、ωm和运动控制器指令τ*。
为了便于后续分析电机动态特性对机器人运动的影响,对关节电机的运行工况进行一定分析。
图2(a)和图2(b)分别为机器人奔跑的联合仿真中各关节电机的转矩-速度状态图和对应的机器人构型。从图2(a)可以看出,由于机器人运动的周期性,各个关节的工作点都以近似圆周的形式周期性变化,这与带标准惯性负载的电机在转矩-速度状态图显示出的椭圆形轨迹相似。对其中髋关节和膝关节电机转矩的傅里叶分析可知,髋关节和膝关节转矩变化频率中最主要的分别是5 Hz与10 Hz,如图3所示。这是由于机器人的运动控制器设计中使步频固定为5 Hz。
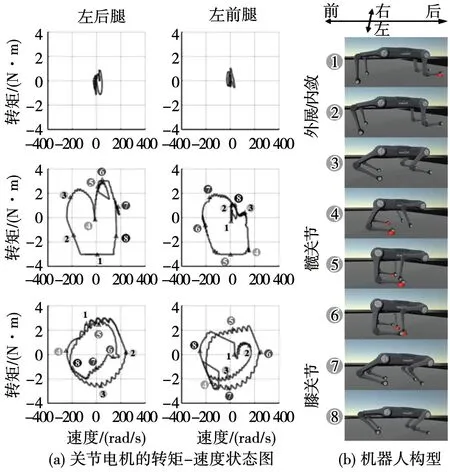
图2 奔跑过程中关节电机转矩和速度仿真结果Fig.2 Simulation results of joint motor torque and speed during running

图3 关节转矩的频谱分析Fig.3 Spectral analysis of joint torque
图1中的联合仿真系统存在运行速度较慢的问题,运动1 s的仿真需要的计算时长约55 min,一方面是由于两个不同的仿真平台进行数据交互时需要频繁读写数据文件,另一方面是由于电机的动力学模型中电流变化的特征时间为R/L,相较于刚体动力学系统的特征时间较长,因此联合仿真时为了得到准确结果需要将仿真求解的步长设置得很小。此外,如果缺乏对电机动态特性的了解,很难在电机及控制器方面进行改进以满足机器人动力学的需求从而达到更高的奔跑速度。
2 电机特性分析
对于联合仿真系统计算时间长和电机动态特性不明的问题,本文在机器人运动控制系统中常用的PI式电机控制器基础上,通过选择d轴电压优先与反馈抑制抗饱和方案来得到一个准确有效、易于计算的电机特性,以方便对运动控制器训练和评价。
关节电机驱动系统包含电机及其控制器,首先分析电机本身的动力学模型和工作情况。采用的表贴式永磁同步电机动力学模型可表示为:
(2)
其中:u,i分别为电机的电压和电流;下标d, q分别为正交的直轴和交轴上的分量;τ为电机的输出转矩;ω为电机的电角速度,ω与电机转动的机械角速度ωm存在比例关系ω=pωm,参数p,R,L,ψf分别为电机的极对数、电阻、电感和磁链,这些参数与运行工况无关。
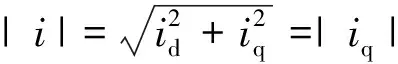
(3)
控制电压的产生方面,在本文的硬件实现中使用桥式逆变电路并采用SVPWM调制方式[16]将直流电压udc转换为交流电输出,因此为了满足调制后的实际控制电压和电压指令值相等,即
(4)
(5)
对于关节电机驱动系统中的控制器,采用离线控制方式,首先计算出包含前馈项、反馈项和抗饱和项的初步电压值ud1和uq1,如式(6)所示。
(6)
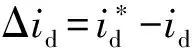

(7)
注意到d、q轴电流id各自受d、q轴电压ud和uq影响,而式(7)对初步电压值ud1和uq1限幅时优先提供了ud1的输出,即优先保证d轴电压ud供应,从而在更大范围内满足id=0。
另外由于控制器采用的抗饱和措施是在初步电压值ud1和uq1的前馈项和反馈项基础上添加了反馈抑制抗饱和项[16],而不是简单地对前馈项和反馈项的和进行限幅,这种方法为后续电机输出特性的简化提供了基础,将在下文详述。
将电机的动力学模型式(2)、电机控制器式(6)与式(7)、控制电压式(4)和控制参数联立可得:
(8)
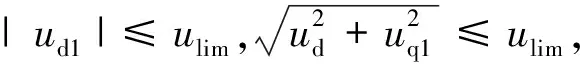
(9)
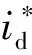
而足式机器人运动速度高时,会出现电压饱和的情况。根据设计,机器人奔跑时关节电机的机械角速度有|ωm|<ωmmax,假设此时控制器仍满足式(3),电压不饱和时Δud=0,代入式(6)有:
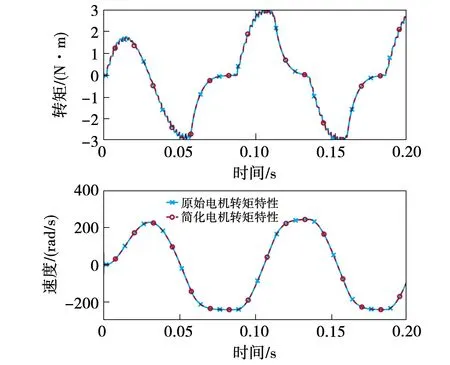
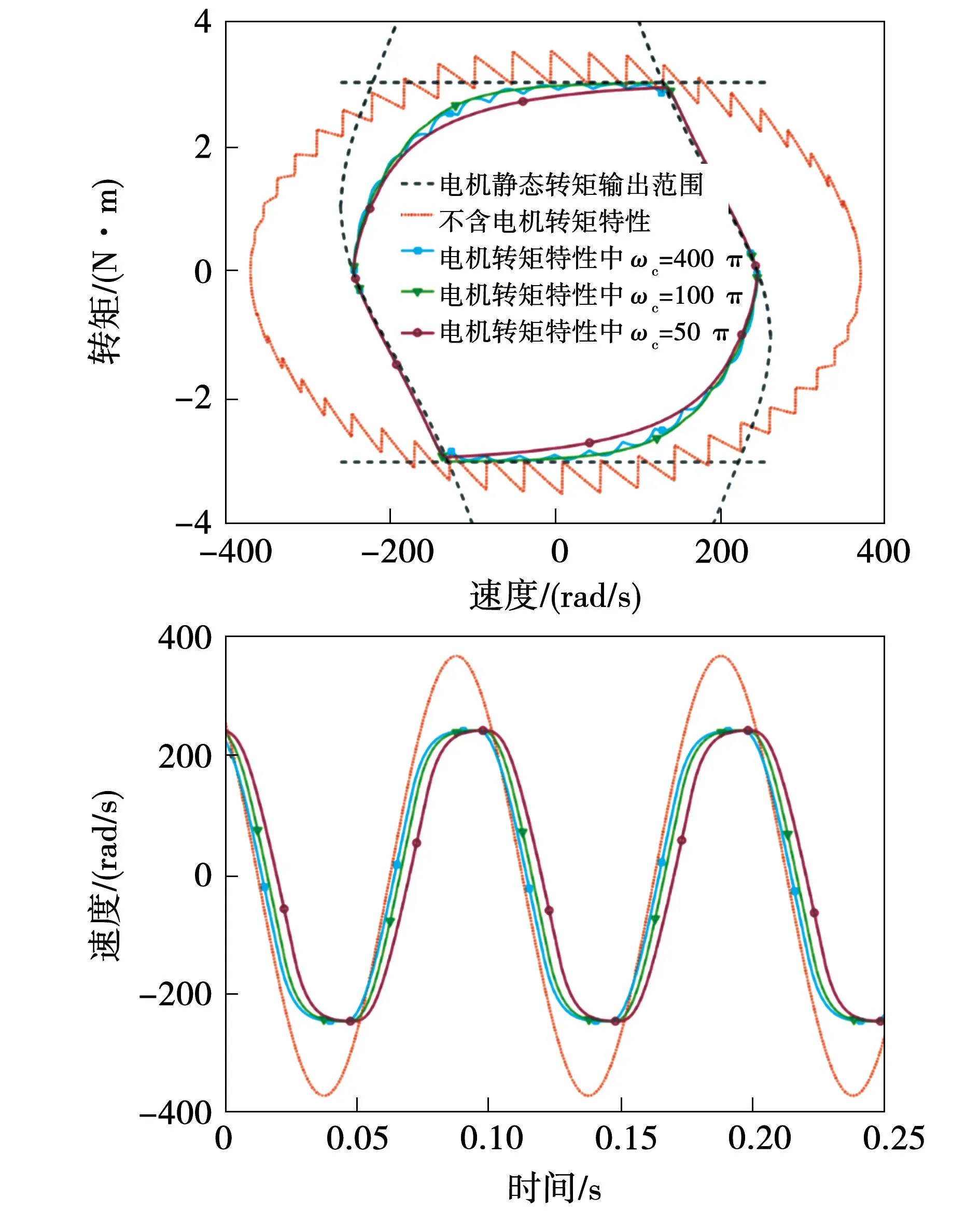
|ud1|=|pLωmmaxiqlim| (10) 式(10)表明电压饱和时d轴电压依旧在ulim范围内,仍然满足Δud=0。因此电压饱和情况下式(7)可简化为: (11) (12) 式(12)左侧的积分值乘上-L/R即可得到方程的右侧,在初始积分值为0时要满足这一点需要方程两侧同时为0,可得: (13) 由此可知,在计算ud和uq的值时,包含积分值的反馈项部分可完全由iq和Δiq表示,而不计算其积分值: (14) 将式(14)与式(2)的q轴部分联立,并由sgn(uq)和sgn(uq1)相同,可得: (15) 其拉氏变换为 (16) 综上所述,简化后的电机转矩输出特性统一用下式计算: (17) (18) 为了分析关节电机在足式机器人高速奔跑工况下表现出的转矩输出特性及其对关节转矩、速度、角度的影响,在同一个工况下对包含式(17)所描述的电机输出特性和不包含电机特性(即认为τ=τ*)的仿真结果进行比较。 图4 正弦位置跟踪仿真系统框图Fig.4 Block diagram of sinusoidal position tracking simulation system 图5给出了包含式(17)所描述的电机输出特性的电机转矩和速度,转矩曲线由于θ*的频率为较低的500 Hz而出现锯齿状波动,但由于惯性负载的低通滤波作用,速度曲线未出现明显纹波;在电机速度接近峰值时,转矩曲线出现的快速下降使得电机速度在峰值出现饱和。此外,简化后的电机转矩计算结果和原始的电机转矩计算结果一致性很好,表明式(17)所描述的简化电机特性与原始的式(8)的所描述的电机动态特性的差异很小,式(3)成立的假设是合理的。 图5 采用简化前后电机特性的转矩和速度仿真结果Fig.5 Simulation results of torque and speed using simplified and original motor characteristics (19) 图6 改变控制参数ωc时的关节转矩和速度Fig.6 Joint torque and speed when changing control parameter ωc 式(19)对应了电机转矩所受的电压和电流限制,也分别对应图6中的上下两条水平直线和左右两条曲线。 由图6(a)可知,电机特性主要表现为,输出转矩在电压限制之内时,表现为转矩指令的低通滤波。而在受电压限制时,从图中可以看出转矩实际值可能超出静态输出范围限制,但基本在其范围内。图6(b)显示,受电压限制带来的电机输出转矩减小会明显影响电机的转速,在正弦指令频率10 Hz、负载惯量135 kg·mm2的工作条件下,转速峰值比不考虑电机特性的情况低约35%。 此外,虽然图6表明控制参数ωc的变化会影响不受电压限制下的转矩输出,但在ωc高于100π rad/s(即50 Hz)时电机速度和位置对ωc的变化不敏感。这表明即使是采用与knee关节(小腿在各关节所接的连杆中转动惯量最小)相近的惯性负载,相应地,机械对电机的控制带宽需求也较小。 在前文得到的简化后的电机动态特性并验证了计算的准确性后,本文将其应用到图1中所示的联合仿真系统中,用于分析电机动态特性对于仿真结果的影响。具体做法是比较包含电机动态特性的仿真(即图1所示的系统中电机特性部分采用式(17)计算)与不含电机转矩特性(即图1中的电机特性部分直接设为τ=τ*)的仿真结果。本文选取了使用典型的bounding步态进行高速奔跑时机器人的速度进行比较。 图7展示了仿真中包含电机特性与否对奔跑速度的差异,图中4条曲线属于两组仿真,分别是在2 m/s和5 m/s的奔跑速度指令下的结果。从中可以看出,在较低的运动速度(约2 m/s)下,是否包含电机特性对机器人的速度没有影响,而在较高的运动速度(约5 m/s)下,包含了电机特性的机器人的运动速度略高于不含电机特性的仿真结果。 图7 包含与不含电机特性的机器人奔跑速度Fig.7 Running speed of robots with and without motor characteristics 为了研究高速下电机特性对奔跑速度带来差异的原因,对机器人奔跑中各关节的转矩、转速等工况进行了分析。图8显示了包含与不包含电机特性的仿真中,机器人右前腿髋关节和膝关节的转矩、速度曲线。白色和阴影背景分别表示对应的腿部处于设计的摆动相和支撑相。转矩曲线中表示的电机静态输出范围的曲线是由速度曲线按式(19)算出。 图8 包含与不含电机特性的右前腿髋关节和膝关节电机转矩、速度曲线Fig.8 Torque and speed curves of the front right leg joint with and without motor characteristics 由图8中的摆动相和支撑相的转换时刻与触地时刻(速度关节产生突变处)比较可知触地时刻不一定位于白色部分转为阴影部分的交界线,而是会稍微提前。此外,由于仿真中不能保证足部在触地后始终紧贴地面,因此在触地相中可能出现再次触地的情况。 比较图8中电机的转矩实际值可以看出,包含电机特性与否会造成的实际转矩差异表现在两方面,一是包含电机特性时转矩峰值被限制在约3 N·m,这出现在髋关节从支撑到摆动的离地时刻,膝关节摆动相中;二是包含电机特性时在较高转速下的转矩输出受限,均出现在两个关节中摆动相中,但膝关节出现了两次,更容易受影响。上述二者分别对应着电机的电流限制和电压限制。 虽然电机特性明显影响了电机转矩实际值,但是否包含电机特性在机器人的奔跑速度上并没有造成很大的差异,图7中高速情况下的速度曲线形状仍基本吻合。比较图8中的关节电机速度曲线差异可知,一方面转矩峰值上的差异只在较短时间内改变了关节速度变化的斜率,另一方面转矩输出受高转速限制,虽然使得膝关节的速度峰值减小,但由于此时处于摆动相,关节速度和转矩的差异反映在机器人摆动腿的运动状态和构型,而几乎不影响机器人支撑腿的触地和离地,因此对奔跑速度影响很小。 本文在BlackPanther四足机器人平台[18]上采集并分析了关节电机的转矩数据,以进一步验证仿真得到的受电压限制的静态转矩输出范围对电机的输出转矩和转速有明显限制作用的结论。 图9是使用永磁同步电机搭建的BlackPanther四足机器人以Trot步态在接近5 m/s的速度奔跑的图像,左右两张图分别对应右前腿处于摆动相和支撑相的开始时刻。机器人的结构和关节配置与前述联合仿真中采用的一致,直流供电电压为24 V,电机控制器采用积分限制抗饱和的PI控制器,转矩输出数据由关节电机上采样电阻采集的电流数据和电机转矩系数转换获得。 图9 BlackPanther四足机器人Fig.9 BlackPanther quadruped robot 实验测得的结果如图10所示。图10中实验数据的蓝实线为右前腿的髋关节和膝关节的电机转矩输出,橙虚线和绿色圆点实线是按照电机转速分别用24 V和16 V供电电压计算出的电机静态转矩输出范围,白色和阴影背景表示对应的腿处于设定的摆动相和支撑相。 图10 实验中右前腿髋关节和膝关节电机转矩曲线Fig.10 Torque curve of the right front leg hip joint and knee joint motor in the experiment 由图10可以看出,电机转矩基本都处于受电压限制的静态转矩输出范围中,髋关节和膝关节在图中圆圈处的电机转矩都明显表现出受转矩输出范围的限制带来的减小,这些区域蓝实线表示的电机转矩与绿色圆点实线曲线基本贴合,而与橙虚线形状一致但存在差值。推测此差值来源于机器人在高功率奔跑过程中,大电流在流经电源管理板和供电电池间长电源线的导线电阻、电源管理板的电阻、电源管理板与各电机驱动器之间及电源线上的接插件接触电阻时产生了不可忽略的压降,导致电机端供电电压偏低。 由上述分析可知,关节电机转矩的实验数据中明显地表现出在较高速度下受电压限制的静态输出范围限制。为了实现机器人运动控制算法从仿真到实物的有效迁移,就需要在仿真系统中加入电机转矩范围或更加细致的电机转矩动态特性。 本文对电机驱动的足式机器人,建立了电机动态特性+机器人动力学的联合仿真系统。通过对电机控制器的设计和电机动态特性的分析,得到与电机动态特性基本一致的简化电机特性。通过单个关节电机摆动和机器人奔跑仿真结果的分析,得出了以下结论: 1)采用d轴电压优先及反馈抑制抗饱和控制器的关节电机的动态特性表现为受静态输出范围限制的一阶低通滤波的特性。 2)在足式机器人的低速奔跑中,关节电机的转矩特性对其运动的速度和稳定性几乎没有影响,此时足式机器人的动力学特性主要受机械惯性主导。 3)在足式机器人高速奔跑中,关节电机特性中的低通滤波频率参数对电机的输出转速影响不大,但电机受电压限制的静态转矩输出范围对电机的输出转矩和转速有明显的限制作用。 4)高速奔跑工况下,受电机特性作用而产生的仿真与实验的转速和角度差异会阻碍运动控制器从仿真到实验的迁移,在运动控制器的训练和优化中应予以考虑。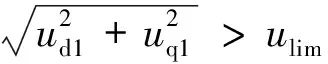
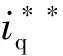
3 电机特性对运动的影响
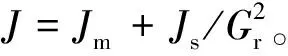
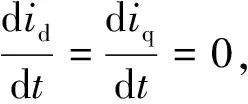
4 电机特性对运动的影响


5 实验分析


6 结 论

