机车充风能力对重载列车缓解性能及车钩力影响研究

魏 伟，张 渊，张 军，赵旭宝，田 野

(1.大连交通大学机车车辆工程学院,大连 116028; 2.中国铁路太原局集团有限公司科学技术研究所,太原 030013)

引言

机车充风能力是指当列车制动后列车管压强降低,或者制动系统处于无压力状态,机车主风缸经过中继阀给列车管及对应车辆制动装置充风的过程,这里的充风能力特指在某时间段内列车管压强上升值,充气能力越强,列车管压强上升速度越快。

在普通列车上,由于操纵方法灵活性较大,充风能力差异对列车操纵方法与安全性影响较小,列车充风能力问题一直未引起关注。对于重载列车,由于列车较长,充风能力可能会带来重载列车以下几方面的变化:(1)充风能力差异会造成列车缓解传播特性变化,使列车纵向冲动发生变化,进而影响列车运行安全;(2)重载列车操纵方法调节空间很小,充风能力的差异使固定操纵方法的实施更加困难,对司机驾驶水平提出更高的要求,如2万t重载列车必须采用模式化操纵,充风不足就会影响模式化操纵,不按模式化操纵就会造成列车停车,严重影响运输效率;(3)重载列车充风能力直接影响长大坡道循环制动操纵策略,由于充风慢,下坡区间列车涨速快,在列车达到限速前必须采取制动措施,因此会造成下一把闸制动力不足,需要追加制动,并停车缓风,影响运输效率;(4)充风能力对重载列车操纵方法具有决定性作用,某些情况下就是因为列车充风能力的不足,被迫采用其他操纵方法,以避免列车充风不足造成列车超速或者失控的风险。因此列车充风能力对于重载列车十分重要。

针对机车充风能力研究工作较少,高胜利[1]针对朔黄铁路万吨列车充风能力不足的问题,通过调整机车电制动和空气制动的主辅关系,将电制动为主的操纵方法改变为以空气制动为主的操纵方法,采用长波浪操纵方式,尽量降低空气损耗,避免了充风不足的问题。刘志国[2]针对HXD2机车充风能力不足的问题,采用提高压缩机启动和关闭压强的方法增加气源供给能力从而提升机车的充风能力,较好地解决了HXD2机车用于2万t列车充风慢的问题。黄印章[3]针对ND5机车充风慢的问题,从中继阀入手,通过减小中继阀下腔列车管入口封堵的孔径,充风时使中继阀勾贝移动距离增加,进而加大充气阀充气孔实现加快充风速度的目的。

使用仿真方法研究列车制动系统在国内外开展了一系列研究工作,美国在20世纪70年代开始列车空气制动系统仿真研究工作,于2013年开发出最新机车与车辆制动系统模型[4-5],印度完成了真空制动系统仿真模型[6],意大利、波兰、乌克兰等国也开展了制动系统的仿真研究工作[7-9],巴西还将并行算法引入列车空气制动仿真系统中[10]。中国在20世纪90年代开始制动系统仿真研究工作[11],建立了中国列车使用的KZ1、120分配阀组成的列车空气制动仿真系统[12-13],制动模型中较详细地建立了车辆阀模型,将车辆阀内弹簧,各种孔径和活塞重力、面积等均作为变量在模型中体现,具备分析各种阀内参数对制动性能影响的能力。黄晓旭[14]建立了旅客列车电控制动系统模型;杨树[15]建立了CCBII 机车自动制动机模型;曾军[16]基于AMESim商业软件建立120控制阀模型。尽管许多国家开展了空气制动仿真研究工作,能将空气制动仿真工作引入列车纵向冲动研究中的国家仅有美国,意大利和中国[4,17-18],并且由于各国采用的制动系统原理不同,这些程序系统不能够用于分析他国的列车制动特性。目前,关于机车充气能力的工作主要是针对现场问题,分析发生原因并寻找解决方法,从仿真模型上研究机车充风能力,以及列车充风能力与列车缓解特性和车钩力相关性研究目前未见报道。

本文研究使用在国际纵向动力学评测中获得优异成绩的列车空气制动与纵向动力学仿真系统TABLDSS[19]开展仿真研究工作,针对重载列车分析机车充风能力与列车缓解波速、车钩力间的关系,并针对机车充风能力提出建议。

1 机车自动制动机模型

将机车自动制动机模型简化为1个主风缸、1个均衡风缸、2个压缩机,以及调整阀和中继阀,模型如图1所示。总风缸有3个进排气口,分别连接压缩机、列车管和均衡风缸管。均衡风缸设置2个进排气口,分别是进气口φ1和排气口φ2,列车管设置进气口φ3和排气口φ4。压缩机模型简化为等质量流量模型。调整阀根据手柄位置调整均衡风缸进排气,中继阀根据均衡风缸和列车管压强差调整列车管的进排气,模型参考文献[20]。

图1 机车自动制动机模型Fig.1 The model of locomotive automatic brake

充气缓解时,调整阀控制φ1,中继阀控制φ3;制动时,调整阀控制φ2,中继阀控制φ4。

列车管充风速度主要决定于φ3孔的大小,其表达式如下

φ3=f(pp-pj)

(1)

(2)

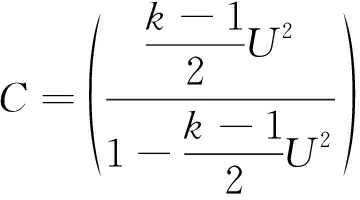
(3)

(4)

式中,pp为列车管压强;pj为均衡风缸压强;pc为主风缸压强;U为无量纲流速;F为管路截面积;k为比热比。首先根据气体流动理论[20]计算制动系统中每个管路网格点和缸室气体状态黎曼变量,再根据黎曼变量与气体物理参数间关系获得气体物理参数,如压强、密度等,再根据式(1)计算当前步列车管充风孔径φ3。当主风缸流向列车管的气体流速为亚音速时,根据式(2)、式(3)计算缸与管连接边界的状态,然后根据式(4)计算质量流量,再由缸内质量计算出缸内气体压强等参数。在主风缸向均衡风缸和列车管充风时,主风缸压强会下降,根据主风缸压强下降程度,压缩机可能处于不工作、1台压缩机工作和2台压缩机工作三种状态,压缩机开启条件参考文献[20]。

式(1)中主风缸与列车管风缸连通的充气孔径φ3和均衡风缸与列车管压强差相关,其关系为一个函数,当修正函数时就可以改变两者关系,进而调整列车充气能力,本研究就是调整两者间关系实现列车不同充气能力的仿真分析。

2 机车充风能力对缓解波速和车钩力的影响分析

仿真列车选用大秦铁路2万t列车,编组形式为1机车+105车辆+1机车+105车辆+可控列尾。考虑到2万t列车在常规运行时仅使用减压50 kPa制动,并且缓解是大车钩力的主要工况,也是事故的主要原因,所以计算工况选择列车先减压50 kPa制动后缓解,计算中按照从控机车和可控列尾与主控机车时间差的试验结果,设置从控机车和可控列尾与主控机车动作时间差为2 s。程序中默认参数(孔径系数1.2)的列车充气能力与真实列车非常接近,默认孔径面积乘以孔径系数即为实际的充气孔面积。程序中默认孔径面积不变,通过调整孔径系数可以实现调节列车充风能力的目的。由于机车和附近车辆列车管压强上升很快,用前部车辆列车管压强评价充风能力很难区分充气速度差异,因此选择尾车列车管压强变化作为充气速度的评价依据。计算了多种孔径系数的列车制动后缓解再充风情况,孔径系数分别为0.1、0.2、0.4、1.2、2.2、5.2六种方案的尾车列车管压强曲线如图2所示。

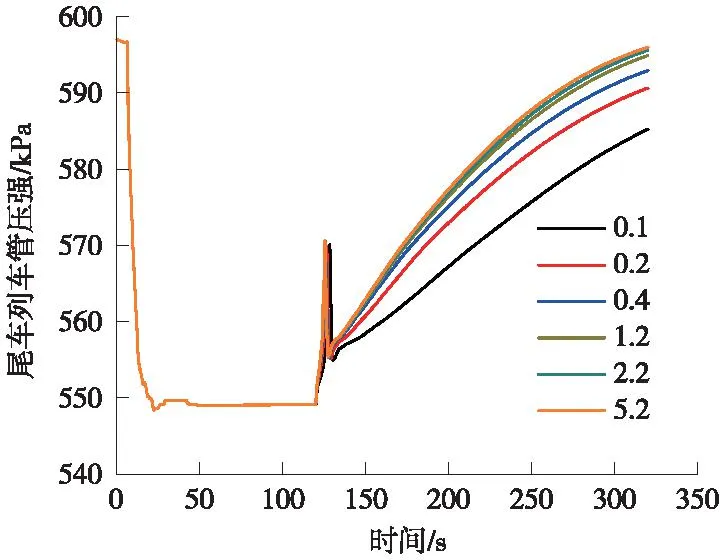
图2 6种孔径系数的尾车列车管压强Fig.2 The pressure of tail train pipes with 6 different charging diameter coefficients

从图2中可以看出,在制动阶段(120 s以内),各种充气孔径系数的列车管压强完全一致,即充气孔径系数对制动阶段列车管压强没有任何影响。在120 s时列车管压强开始上升,当列车管压强开始上升后,列车管压强出现突然上升又回落的尖峰,这个尖峰是车辆控制阀中加速缓解阀动作后,加速缓解风缸向列车管充风而产生,待加速缓解功能结束后,列车管压强回落,然后列车管压强缓慢上升。由于充气孔孔径不同,列车管压强上升呈现不同的上升速率,充气孔径越小,列车管压强上升越慢。从列车管压强上升速度看,充气孔径对充风速度的影响不是线性的,充风系数在0.1～0.4间充风能力差异明显,当充风系数在2.2以后,充风能力差异很小。在列车管压强达到580 kPa以前,各压强曲线线性度较好,此外现行标准中规定580 kPa作为列车充满风的判断标准,因此,选择从列车管开始充风到列车管压强达到580 kPa的时间差作为比较指标,绘出了各种孔径条件下充风时间曲线,如图3所示。由图3可以看出,列车充风能力与充气孔径间的非线性关系,即充气孔径系数在2.2以后,充气时间变化不大。在充气孔径系数在0.4以下时,充气孔径影响很大,充气孔径越小影响越大。

图3 各种孔径系数的充风时间Fig.3 The charging time for various charging diameter coefficients

因为机车充气能力影响列车中管路气体的压强上升速度,进而影响车辆的缓解时间,不同的充气能力条件下各车辆缓解时间会有所差异,为此,提取每种机车充气孔径系数条件下每个车辆控制阀开始缓解的时间,并且绘出每个车辆开始缓解时间沿车长分布,如图4所示。图中1车和107车附近车辆缓解开始时间较早,这是因为这两部分车辆与主控机车或从控机车紧邻。从缓解传播规律看,主控机车向后传播,从控机车向前后传播,在两机车中部车辆在缓解波相遇时的车辆动作时间较晚(相对于两机车中部的其他车辆),此外,从控机车后部车辆由于仅有从控机车充风,缓解传播较慢,最晚动作车辆约位于列车尾部。列车前部车辆缓解开始时间几乎不受充气孔大小的影响,而从控机车后部车辆受机车充风能力影响最为显著,特别是尾部附近车辆,从图4中可以看出,首尾车开始缓解时间差随着机车充风能力的降低在逐渐增加。在本文分析范围内,首尾车时间差最大相差3 s,对于重载列车,这将会明显增加缓解过程中的车钩力。

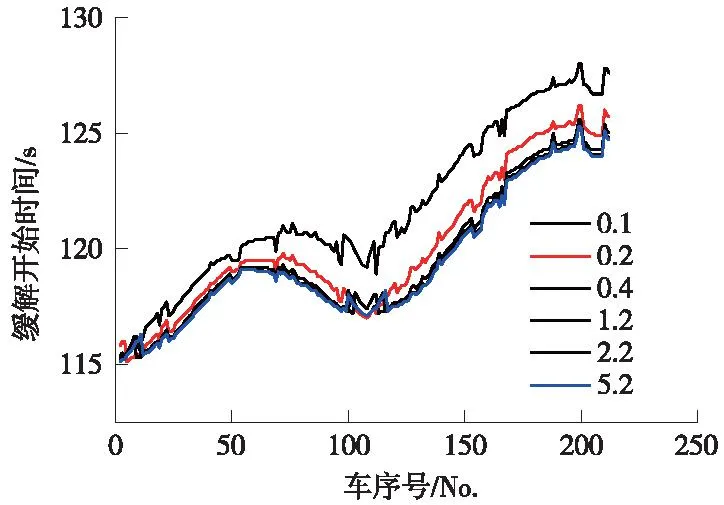
图4 各种孔径系数的缓解开始时间Fig.4 The release start time for various charging diameter coefficients

图4中每个曲线并不光滑,即相邻车辆可能缓解时间有较大差异,经过分析发现,相邻车辆缓解时间有较大差异是因为制动后各车辆控制阀进入保压位时间不同,致使缓解前副风缸压强不同所造成,副风缸压强越高,开始缓解时间越晚。

由于缓解时间的差异,造成列车纵向冲动,图5为各种充气孔径系数条件下最大车钩力沿车长分布曲线。

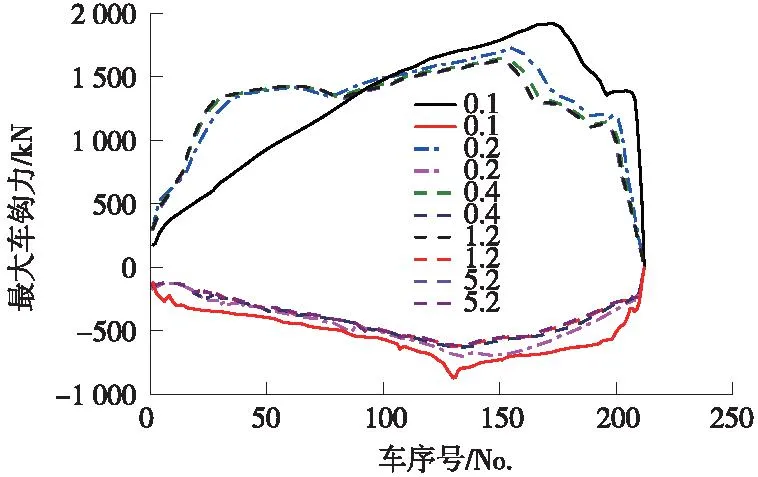
图5 各种孔径系数的列车车钩力Fig.5 The train coupler force with various charging diameter coefficients

图5中车钩力沿车长分布曲线是制动与缓解过程中每个车辆受到的最大拉伸车钩力和最大压缩车钩力连线而成,代表了列车中最大车钩力沿车长的分布规律。由图5可见,制动缓解过程中拉伸车钩力明显大于压缩车钩力。首先分析拉伸车钩力,随着充气孔径系数的降低,最大拉伸车钩力增加,当充气孔径系数为0.1时,最大拉伸车钩力为1 922 kN,发生车位为172(序号包含机车,以下同),后半列车(1万t)车钩力明显高于前半列车。随着机车充气孔径系数增加,最大拉伸车钩力逐渐减小,最大拉伸车钩力的发生车位有所前移,前一小列车拉伸车钩力明显增加,后一小列车拉伸车钩力减小。当充气孔径系数为0.2及其以上时,拉伸车钩力总体趋势一致,最大车钩力随着充气孔径系数增加逐渐减小,发生最大车钩力车位缓慢前移。当充气孔径系数达到0.4时,最大拉伸车钩力为1 609 kN,相对于充气系数为0.1的车钩力降低16.2%。随着充气孔径系数再继续增加,车钩力增加非常缓慢,因此,可以认为当充气孔径系数为0.4时,车钩力基本不随充气孔径系数而变化,可以将0.4作为未来重载列车充气孔径系数的最小值,以这个值作为限定值可以保证重载列车充气孔变化时车钩力基本不变。

从压钩力曲线看,在充气孔径系数为0.1时,车钩力最大,最大压缩车钩力872 kN,发生在130车,当充气孔径系数为0.4或者以上时,压缩车钩力基本不再变化,这也说明从压缩力角度出发,充气孔径系数0.4作为重载列车充气限值比较合适。

从图2和图3中列车管充气曲线和充风时间可以看出,随着充气孔径系数减小,充气时间在延长,并且变化规律为非线性,当充气孔径系数为0.4以下时,充气孔径系数对充风时间影响非常明显,当充气孔径系数大于0.4时,影响逐渐减弱,当充气孔径系数达到2.2及以上时,充气孔径系数变化,充风时间几乎不再变化。从图5充气孔径系数对车钩力影响曲线也可以看出,在充气孔径系数0.4及以上时,车钩力几乎不再变化,因此,选取0.4作为充气孔径系数最小值可以保证车钩力不再随充气孔径系数变化,充风时间也比较稳定,即列车的缓解传播时间、车钩力、充满风时间将基本固定。

3 机车充风能力评判标准探讨

随着铁路运输技术的不断进步,各种规章制度在不断完善,但是在列车充气能力上一直没有标准要求,由于充气能力对重载列车影响显著,因此有必要针对重载列车提出列车充风能力的要求。

对于上述2万t编组列车,可以通过尾车列车管压强变化确定充风能力。但是由于制动后机车减压量的差异,列车管压强略有不同,如果以列车管压强充到580 kPa或者590 kPa的时间判断可能会由于机车减压量差异出现同一列车充风时间不一致的问题,因此将列车管压强上升相对值作为评价标准更加合适,一般减压50 kPa后列车管压强为550 kPa,上升到580 kPa压强差为30 kPa,上升到590 kPa压强差为40 kPa,因此寻找2万t仿真结果中压强上升30 kPa和40 kPa所需要的时间。以充风系数0.4为例,图2中列车管压强上升30 kPa和40 kPa所需时间分别为99.2 s和161.6 s。上述计时开始时间以尾车列车管压强开始上升为准,考虑机车手柄开始放到缓解位和尾车列车管开始充气的时间差约为10 s,即从机车手柄位移动到缓解位开始计时,大约109 s尾车充风到580 kPa较为合适。上述方法仅适用于2万t组合列车,对于其他列车需要找到通用的方法。

如果使用制动后再充风能力评价列车充风能力,由此制订出列车充风标准存在一定难度,这是因为机车减压量存在波动性,不能保证每次制动减压量完全相同,使得再充风时间也会有所不同,因此用制动后再充风时间描述充风能力有不足之处。为此,尝试使用短列车初充风作为充气评价标准,采用列车编组为50辆,一台机车位于列车头部,初始状态为车辆系统中所有管路和风缸为0 kPa条件下作为充气初始条件,充风系数为0.4情况下计算了短列车充风过程,并使用尾车列车管作为评价测试点。图6为上述短车初充风条件下尾车列车管压强曲线。将尾车列车管达到典型压强所需时间列于表1中。

表1 50辆编组列车充风时间Table 1 The charging time of a 50-car train

图6 50辆编组列车初充风尾车压强Fig.6 The pressure at the tail of train(50 cars) during initial charging

从图6可以看出,列车管升压过程是非线性变化,各阶段上升速率有所不同,在列车管压强达到580 kPa之前(300 kPa以后)列车管压强上升速度基本呈线性增长,在压强达到580 kPa以后列车管充风速度开始变得十分缓慢。在列车管充风速度非线性变化区间内,很难用达到某压强值的时间评价充气能力,所以建议用列车管充风到580 kPa所用时间评价更为合适,即在328 s充风至580 kPa及以上即可判定为合格。

根据上述仿真计算分析,提出用50辆列车编组的初充风时间作为列车充风能力标准的建议。如果机车验收现场不满足组成列车条件,也可以采用等效容积的测试方法,例如可以在机车验收现场做一个等效某固定编组列车制动系统总容积,首先通过仿真方法确定此容积条件下充风速率,经过实验验证后,制订出充风标准;然后各工厂均采用统一的容积、统一检测方法和标准对机车充风能力进行测试。

4 结论

针对重载列车充风能力问题首次使用列车空气制动系统仿真方法分析了机车充风能力对列车缓解特性和车钩力的影响规律,得出如下结论。

(1) 机车充风能力对列车缓解波传播、列车纵向冲动都会产生影响,当机车充气太慢时,列车缓解时间差增加,列车纵向冲动增加。

(2) 鉴于机车充风能力对重载列车的影响较为敏感,建议针对重载列车增加机车充风能力评价标准,在机车交车前检查机车充风能力,保障重载列车安全运行。

(3) 可以采用编组50辆列车初充风时间作为列车充风能力的判断标准,当列车初充风时间在328 s时,尾车列车管压强达到580 kPa及以上作为检测标准。也可以采用等效容积法,采用机车向固定容积容器充风的方法通过记录容器达到某压强的充风时间评价机车充风能力。

(4) 建议针对重载列车充风能力对缓解波速、车钩力的影响开展多部门联合实验与仿真研究,制订机车充风能力的实验方法和标准。