基于岭回归和LASSO回归浅析河南省粮食产量影响因素

□耿 娟，聂文倩

（河北经贸大学数学与统计学学院，河北 石家庄 050062）

“民以食为天，国以粮为本”，粮食对于国家发展至关重要。河南省是粮食生产大省，保证国家粮食安全是一项重大的政治任务。河南省地处平原，有大片耕地，以农业为主，其粮食产量关系到整个国家的命运，因此，需充分发挥区位优势，大力发展农业，保证国家粮食安全。研究河南省粮食生产的主要影响因素对提高粮食生产水平、保证粮食安全具有十分重要的现实意义。

1 文献综述

河南省是我国小麦生产第一大省，是我国的粮食生产核心区。历年来，学者们运用多种方法对河南省粮食产量的影响因素进行分析。刘忠广（2019）[1]利用SPSS 软件和通径分析法分析了河南省粮食产量的影响因素，结果表明，影响因素对粮食产量影响程度从大到小依次是粮食作物单位面积产量、粮食作物播种面积、农村用电量、化肥施用量、有效灌溉面积、农村机械总动力、农村从业人口数，说明增加粮食作物单位面积产量、扩大播种面积、增加农村用电量等可以显著提高粮食产量。张贞等（2017）[2]运用Pearson 相关分析法和灰色关联熵法进行分析，结果表明，影响粮食产量的因素排名从前往后依次是农田有效灌溉面积、耕地面积、粮食作物播种面积、平均气温、日照时数、年降水总量、化肥、农药以及受灾面积。杨娟等（2017）[3]运用主成分分析法分析河南省1978—2014 年的数据，探索建立计量经济模型对该期间影响河南省粮食产量波动的因素进行分析，结果表明，经济发展与农业资本投入、劳动与土地投入、成本—收益对粮食产量的影响排在前三名。李炳军等（2021）运用BP神经网络对河南省粮食产量进行预测，发现河南省粮食生产增速放缓，粮食生产重心北移。张淑华等（2022）用SD-GM 方法对河南省粮食生产科技创新进行分析，提出“科技蓄粮”的建议。

2 数据说明

为研究河南省粮食产量的影响因素，文章主要运用河南省2002—2021 年的数据。为保证数据来源的可靠性，所有数据均来自《河南省统计年鉴》。根据已有研究，取河南省粮食产量（万t）为被解释变量Y，播种面积（千hm2）、灌溉面积（千hm2）、农业机械总动力（万kW）、化肥施用折纯量（万t）分别为解释变量X1、X2、X3、X4，构造多元统计模型如下。

式中：β0是常数项，β1～β4是被解释变量的系数，ε是随机扰动项，且ε服从均值为0、方差为σ2的正态分布。各变量数据描述性统计如表1 所示。

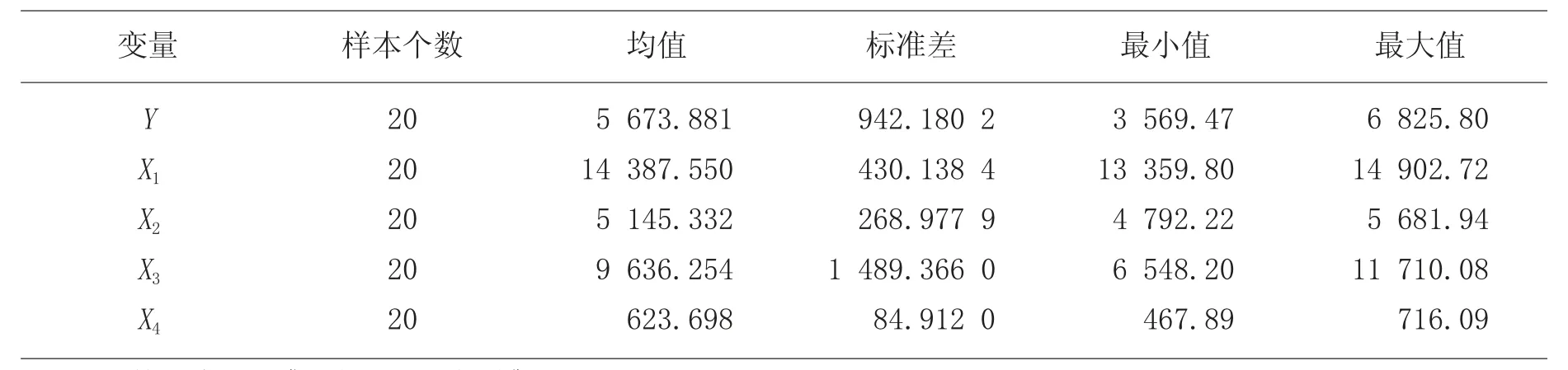
表1 2002—2021 年各变量数据描述性统计

3 实证分析

3.1 多重共线性检验

用SPSS 软件对数据进行多重共线性检验，检验结果如表2 所示。

由表2 可知，有4 个条件指数大于10，所以有充足的理由认为变量间具有严重的多重共线性，此时不适合使用普通最小二乘法估计。因此，使用可以处理多重共线性问题的岭回归和LASSO 回归分析。

3.2 岭回归

岭回归和LASSO 回归可以解决多重共线性问题，考虑到变量量纲不同，进行岭回归和LASSO 回归之前，对数据进行无量纲化处理，主要采用标准化处理。根据岭回归原理分析，运用岭回归求解回归系数可表示为如下。

式中：lambda 是岭回归参数，之后用R软件实现岭回归。制订岭参数lambda 的取值范围是0～1，绘制岭迹图如图1 所示。

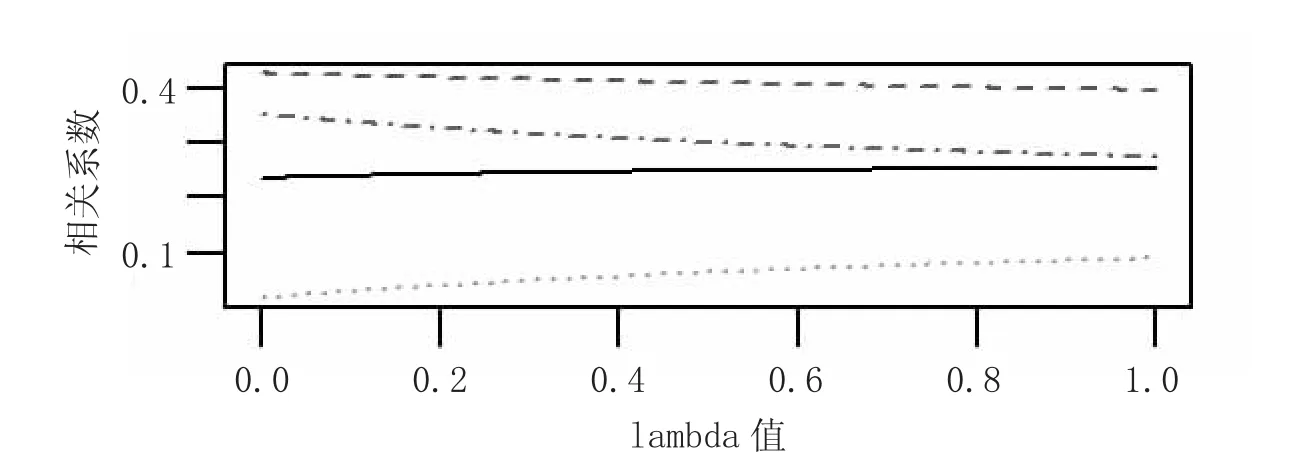
图1 岭迹图

从岭迹图中可以看出，当lambda=0 时，图像不稳定。因此可以说明变量间存在多重共线性。用R 软件中的select 函数查看k值并筛选，选择最小的k值（即lambda）为0.120 511 5，之后使用lambda 值进行岭回归分析，具体结果如表3 所示。

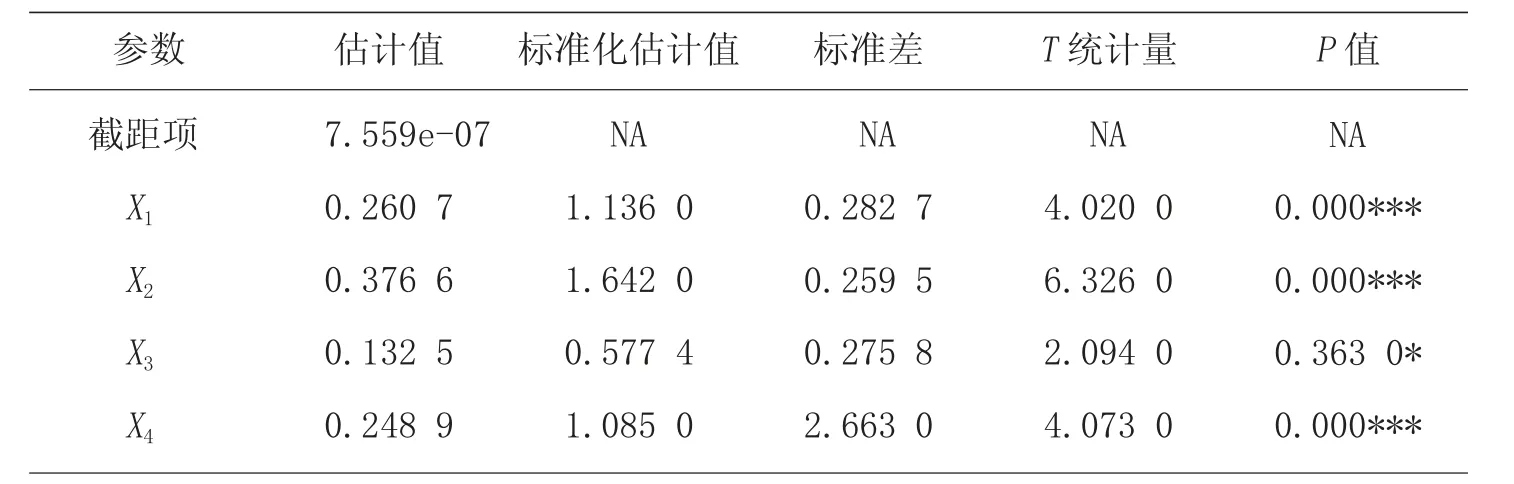
表3 岭回归结果

由表3 可知，标准化后β1、β2、β3、β4的系数分别为1.136 0、1.642 0、0.577 4、1.085 0，并且都在0.05显著性水平下通过检验，标准化后的岭回归方程可以表示为如下。

4 个自变量的回归系数全部为正，说明河南省粮食种植面积、有效灌溉面积、农业机械总动力和化肥施用折纯量与粮食产量呈现正相关，河南省粮食种植面积、有效灌溉面积、农业机械总动力和化肥施用折纯量增加会导致粮食产量增加，这与现实情况相符。解释变量值越大，对被解释变量影响越大。

进一步分析可知，因为β2＞β1＞β4＞β3，所以对河南省粮食产量影响比较大的解释变量依次是有效灌溉面积、粮食种植面积、化肥施用折纯量和农业机械总动力。

3.3 LASSO回归

LASSO 回归也可以解决多重共线性问题。文章选取常用的Cp统计量法进行系数选择，R 语言中有多个包可以实现LASSO 回归，运用R 软件中Lars 算法进行LASSO 回归，得到相应的回归结果[4]。

图2 中的竖线个数对应LASSO 中迭代的次数，对应的系数值不为0 的自变量即为选入模型的解释变量。图2 中共有五条竖线，所以一共进行五次迭代，具体迭代情况如表4 所示。

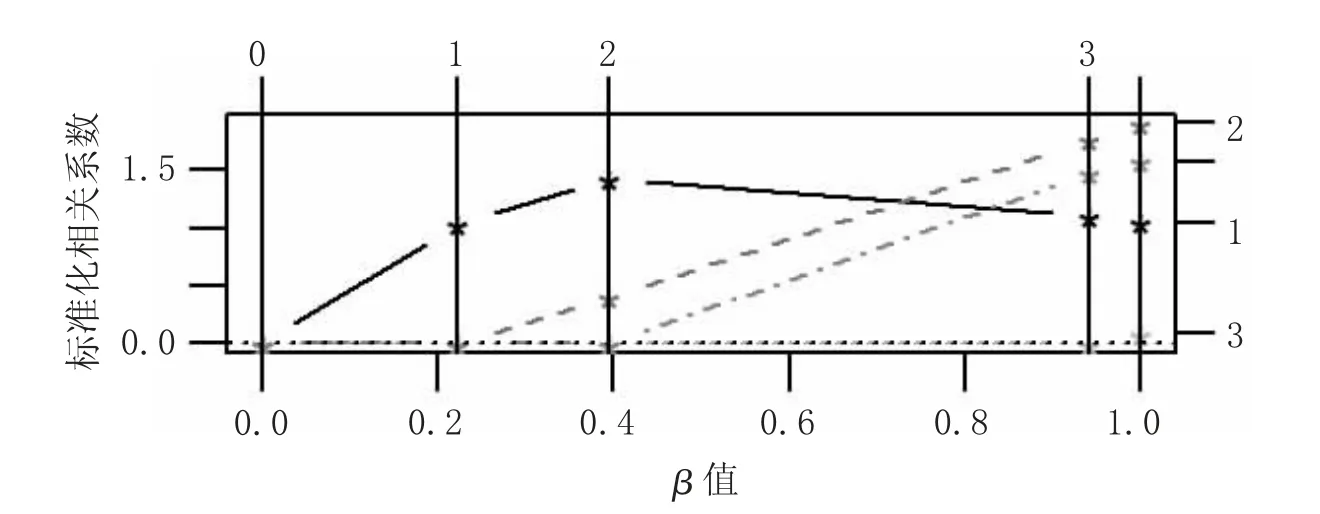
图2 迭代次数

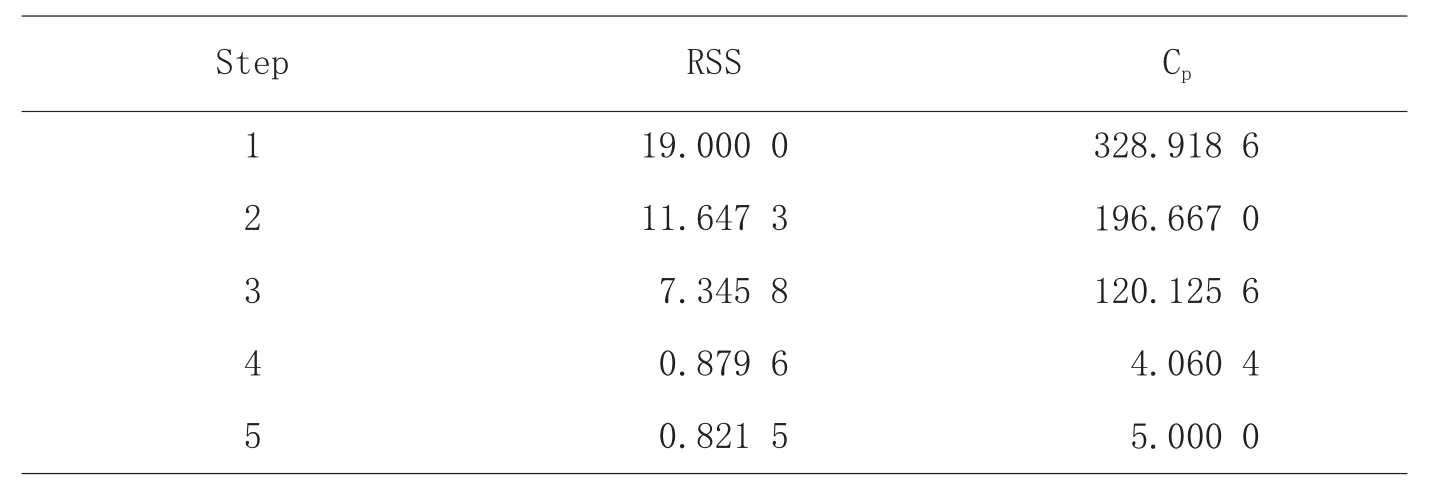
表4 LASSO求解中值的变化

表4 反映了LASSO 求解中值的变化情况，其中Step 表示步数，RSS 表示残差平方和，找到使统计量Cp达到最小值的步数，输出所对应解释变量的系数，从中筛选出系数不为0 的变量。可以看出，当变量选取到第4 步时，Cp值取得最小值4.060 4。

图3 反映了变量筛选结果，显然筛选之后只剩下种植面积、有效灌溉面积和化肥施用折纯量三个解释变量，这与岭回归分析结果保持一致，LASSO 回归分析结果如表5 所示。

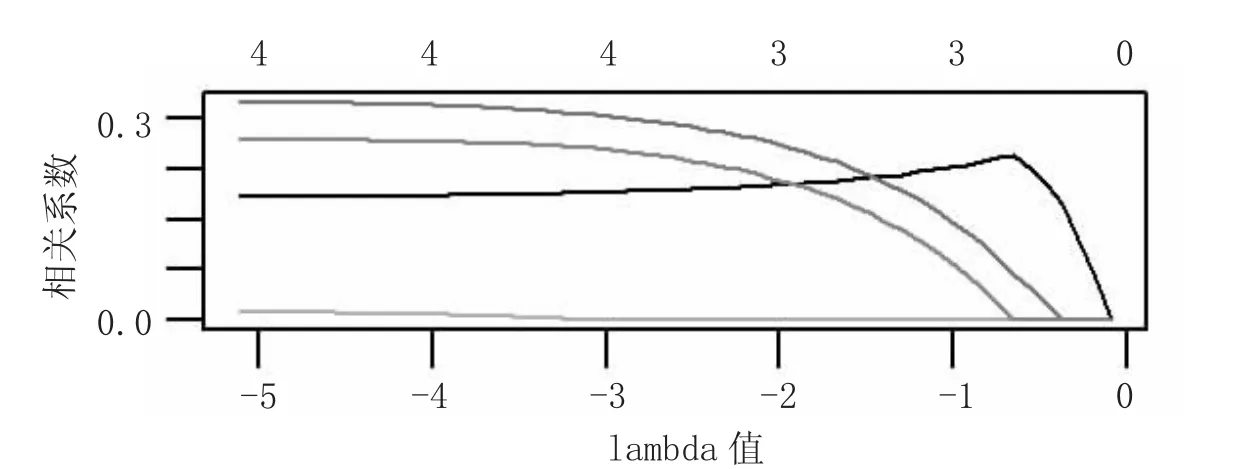
图3 变量筛选结果

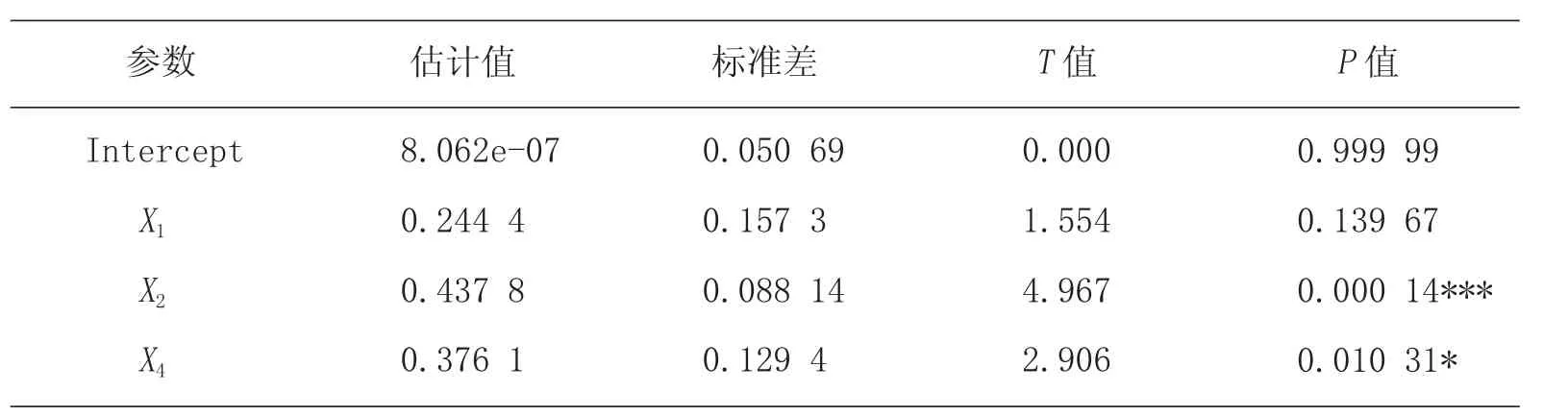
表5 LASSO回归结果

表5 中种植面积、有效灌溉面积和化肥施用折纯量三个解释变量的系数分别为0.244 4、0.437 8、0.376 1，LASSO 回归方程如下。

各解释变量与被解释变量依然存在正相关关系，以上分析结果依然适用。

4 结束语

当前，中国人不仅有能力解决自己的吃饭问题，还能帮助世界人民解决吃饭问题，但这并不意味着我国的粮食安全稳如磐石，保障粮食安全是一条永无止境的路。文章运用岭回归和LASSO 回归对具有多重共线性的数据进行分析，得出以下结论。河南省粮食产量与种植面积、有效灌溉面积、农业机械总动力和化肥施用折纯量呈现正相关关系；对河南省粮食产量影响比较大的解释变量依次是有效灌溉面积、粮食种植面积、化肥施用折纯量和农业机械总动力。可见，粮食种植面积会影响粮食产量，相关部门要坚决守住耕地这条不可逾越的红线，鼓励粮食生产向多元化规模经营方向发展，提高粮食生产效率和质量，发挥金融对粮食产量的保驾护航作用，畅通粮食生产和流通的各个环节。