团簇NiPS3异构转化热力学与动力学分析
宋静丽,方志刚,刘立娥,魏代霞,原 琳
(辽宁科技大学 化学工程学院,鞍山 114051)
1 引 言
随着现代技术的发展与精进,各种材料层出不穷,自从曼彻斯特大学Geim小组成功机械剥离石墨烯[1]以来,以石墨烯为代表的二维材料[2,3]开始引起了人们浓厚兴趣.由于二维材料的厚度很小,它们具有极高的比表面积和机械强度、显著的机械性和光学透明度,由于这些独特的物理、化学性质,二维材料已被广泛的应用于光电器材[4,5]、太阳能电池[6]、传感器[7]、光电催化[8,9]领域.
过渡金属磷酸盐材料[10,11]作为一种新型二维材料,其材料内部表现为层状的晶体结构,不仅具有传统二维材料的优秀性能,更由于内部非金属与过渡金属的耦合,致使其展现出独特的能带和电子结构,具有优异的光学、催化、电子和磁性等物理化学性质.层状NiPS3材料[12]作为众多过渡金属磷酸盐材料的代表,因而具有优异的磁性、电子、光学和催化等物理性质,成为研究热点.在磁学性质领域,Lançon等人[13]用中子非弹性散射测量了粉状NiPS3的磁激发,确定了其磁交换作用强度和各向异性,发现NiPS3是一种准二维反铁磁体.Kim等人[14]利用反铁磁性范德华材料NiPS3,对双磁振子和量子效率形式的磁信号随NiPS3厚度的变化进行研究,发现其反铁磁有序随着厚度的减小而减小.在电子性质应用领域,Kim等人[15]用椭圆偏振光谱、X射线吸收、光电子能谱等多种实验手段对层状NiPS3的电子结构进行了研究,发现它具有很强的电荷-自旋耦合作用,是研究二维磁性材料中关联电子物理的有用候选材料.在光学应用领域,Chu等人[16]利用层数较少的二维NiPS3纳米薄片制作了紫外光探测器,这种紫外光探测器表现出较高的探测率,性能优于一些传统的宽带隙紫外光探测器,具有良好的光电探测器性能.Liu等人[17]制备了少层NiPS3纳米薄片并对其进行研究,发现具有优异的锁模性能,拓展了NiPS3材料非线性光学响应特性的研究.在催化应用领域,Xue等人[18]在水中剥离了块状NiPS3晶体,对其研究发现由于内部金属非金属间的协同效应,导致的活性表面积显著增加,电子转移阻力显著降低,NiPS3材料表现出优异的催化性能.Li等人[19]发现NiPS3材料中S和P原子是析氢反应(HER)和析氧反应(OER)的活性中心,说明NiPS3在水分离方面可做双功能催化材料.
综上所述,不难发现NiPS3材料因其良好的特性,成为科学家们的研究热点,但是目前对于NiPS3材料的分析均局限于宏观实验方面,而微观层面上对NiPS3材料的研究较少.通过查阅文献可知,NiPS3材料的单层结构为无数个小的单元延展而成,小单元的性质决定整体的性质.团簇[20,21]是采用局域化的原子集团模型用以模拟整个晶体在微观上物质构造的一种方法,该模型方法是目前研究非晶态材料局部性质的有效方法.因此本文利用团簇对NiPS3材料进行局域结构的模拟,以此对其进行微观层面研究,期望能够弥补NiPS3材料理论研究方面的空白,为科研人员对过渡金属磷酸盐材料NiPS3进一步的研究以及宏观的应用提供一定的理论支撑和参考.
2 模型与计算方法
2.1 模型设计
根据拓扑学原理[22,23],对团簇NiPS3的空间结构进行设计和分析,以平面五边形型、立体四棱锥型、立体三角双锥型为基础构型,通过改变不同原子的相对位置获得二、四重态下团簇NiPS3的初始构型.采用密度泛函理论[24,25]中的B3LYP杂化泛函[26],对团簇NiPS3中过渡金属元素及开壳层结构进行计算,利用def2-tzvp基组对团簇NiPS3中的各个元素进行全电子运算,其中P和S加极化函数.对所设计出的团簇NiPS3初始构型进行二、四重态下的优化收敛分析,收敛条件为最大作用力<0.00045、均方根作用力<0.00030、最大位移<0.00180、均方根位移<0.00120.最终得到团簇NiPS3可稳定存在的优化构型,并利用IRC方法进行构型验证,确保最终所得的构型为团簇NiPS3的最优构型.上述运行计算和数据处理过程均基于HP-Z440计算机,利用Gaussian09量子化学程序辅助完成.
2.2 异构化计算方法
异构化过程的反应机理为:
过渡态结构是指势能面上反应路径的能量最高点,存在时间极短,很难通过实验方法获得,计算化学方法在目前是预测过渡态的最有力武器.基于优化得出的NiPS3稳定构型,根据过渡态理论,使用STQN算法对构型间的异构转化反应进行计算,使结构从低能量的反应物出发,以ST法假定路径的切线方向为引导,沿着QST法假设的反应路径进行爬坡,使结构到达假设路径的能量最高点处,此时转换为QN法精确寻找过渡态位置,最后输出各优化构型之间异构化反应的过渡态空间结构,对过渡态构型也进行IRC验证.此过程中所运用的泛函、基组和优化收敛条件与2.1节相同.
3 结果与讨论
3.1 团簇NiPS3的优化构型及过渡态构型
团簇NiPS3通过构型的优化计算最终得出二、四重态下的优化构型共10种,如图1所示.以优化构型为反应物和生成物,得出优化构型之间异构化反应的过渡态空间构型(Transition State Configuration,TS)共7种,如图2所示,过渡态构型中白色实键表示反应前后未发生变化的键,白色虚键代表反应过程中断裂的键,绿色实键代表RT反应过程中新生成的键,蓝色箭头的方向和长度表示原子位移的方向和距离.为了便于观察与分析,以所有的构型中能量最低的构型1(2)的能量为基准,将其设为0 kJ·mol-1,其他构型的能量以相对值(列于构型后的括号中)的大小重新排列,其中相对值前括号中的数字表示自选多重度.
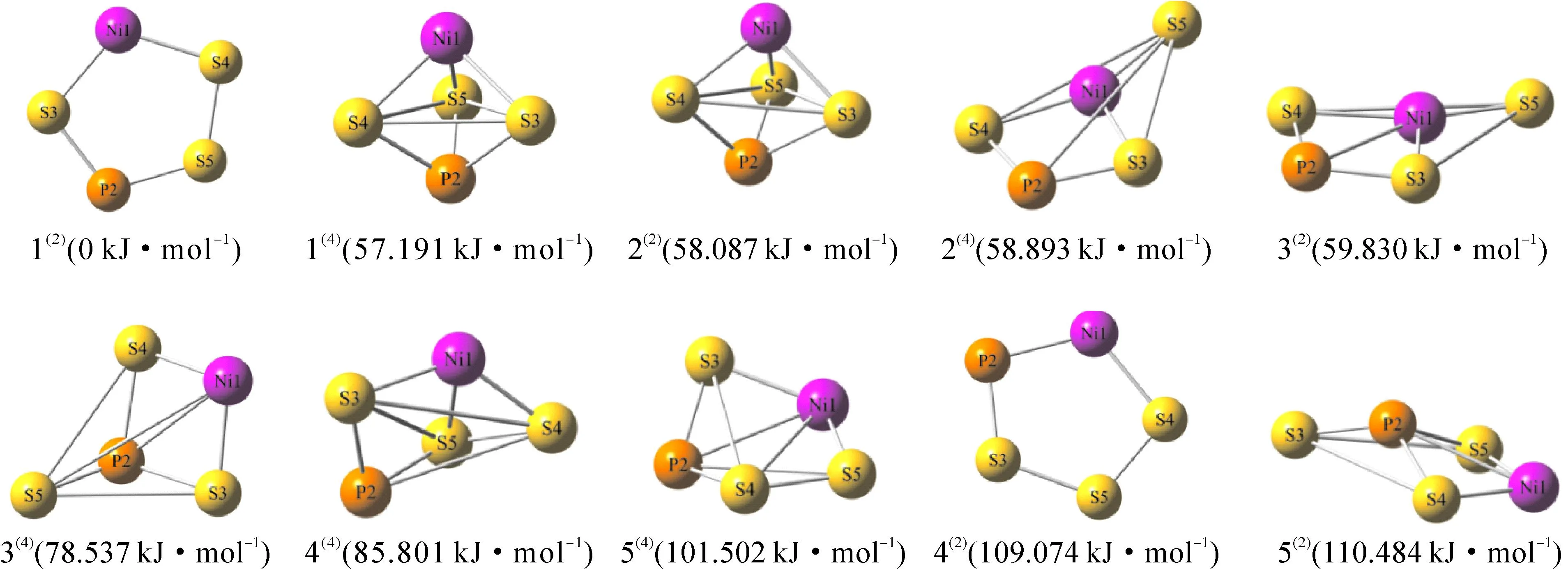
图1 团簇NiPS3的优化构型
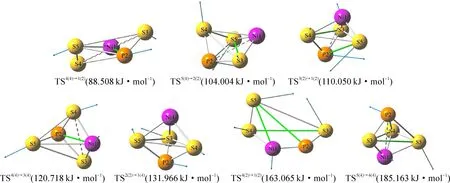
图2 团簇NiPS3的过渡态构型图
观察图1可以发现,团簇NiPS3优化构型的的几何形态以立体构型为主,如四棱锥型(2(4))、三角双锥型(构型1(4)和2(2))、戴帽三角锥型(构型3(4)、4(4)、5(4)和5(2)),平面构型仅有平面五边形型构型1(2)和4(2).由以上分析不难看出,平面型构型仅存在于二重态,说明团簇NiPS3的平面形在二重态下更容易稳定存在.
观察图2,可以发现,过渡态的几何形态全为立体构型,且以三角双锥型构型为主,仅TS5(4)→1(2)为四棱锥.从断键角度来看,在5个发生断键的反应中,仅涉及S-S键和Ni-P键的断裂,4(4)→1(2)(表示构型4(4)向1(2)的异构转化反应,反应命名规则下同)和4(4)→3(4)反应时断裂的为S-S键,另外3个断键异构化反应中均断裂的是Ni-P键.从成键角度来看,在6个有化学键生成的反应中,4(4)→1(2)和4(4)→3(4)中仅有Ni-P键的生成;5(4)→2(2)和5(4)→4(4)中仅有S-S键的生成;3(2)→1(2)中存在S-S键和P-S键的生成;4(2)→1(2)中存在S-S键、P-S键和Ni-P键的生成.同时2(2)→1(4)过程中由于反应物2(2)和生成物1(4)结构相似度较高,TS2(2)→1(4)也为三角双锥型构型,没有出现键的断裂和生成.通过以上分析,团簇NiPS3异构化反应过渡态的稳定存在与非金属-金属和非金属-非金属之间的成键与断键都有关系.
3.2 团簇NiPS3异构化的热力学分析
3.2.1团簇NiPS3的热力学参数
团簇NiPS3不同构型的热力学性质影响其相互之间异构化反应的转化情况,所以为对团簇NiPS3的异构转化进行深入研究,表1列出团簇NiPS3的热力学能(U)、吉布斯自由能(G)、焓(H)及熵(S)等热力学参数,由化学热力学可得G=H-TS、U=H-pV(T为温度,p为压强,V为体积).观察表1的数据可以发现,U和H的大小关系均满足1(2)<1(4)<2(2)<2(4)<3(2)<3(4)<4(4)<5(4)<4(2)<5(2),说明构型构型1(2)和构型1(4)最为稳定,而G和S的大小关系却不遵循此关系,造成此差异的原因是S值的变化趋势不同,对于构型3(2)而言,其熵值最大,系统混乱程度很高,系统有较强的无序性.

表1 团簇NiPS3优化构型热力学参数
3.2.2团簇NiPS3异构化反应的限度和方向
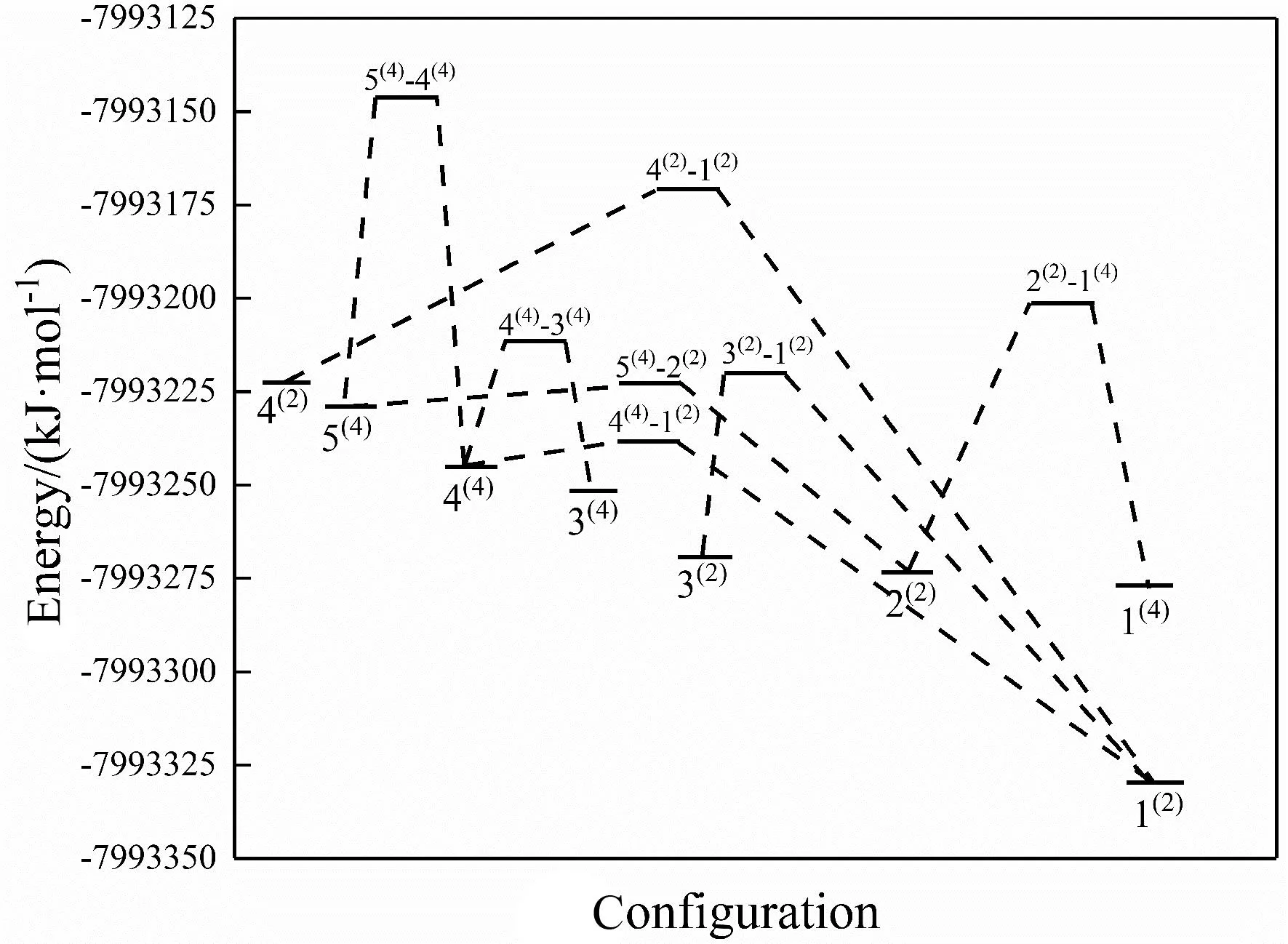
吉布斯自由能是在化学热力学中为了判断反应方向而定义的一种热力学函数,其变化量ΔG可判断各种热力学过程的反应方向和反应限度,是判断反应是否能自发进行的一项重要指标.平衡常数K是可以反映化学反应进行的程度即反应的限度,平衡常数K值越大,表明反应进行的程度越大,反应越彻底;反之则说明反应进行的越不完全.对于一般反应而言,当K>105时,认为该反应正向进行的限度远大于逆向进行的限度,反应进行较为完全;当10-5 (1) 对异构化反应的平衡常数K进行计算,式中ΔH为焓变,ΔS为熵变,R为摩尔气体常数.进而对反应的限度和方向进行讨论.将所有异构化反应的ΔG、ΔH、ΔS和平衡常数K列于表2. 表2 团簇NiPS3异构化反应的平衡常数 观察表2中各异构化反应ΔG的数据,发现异构化反应的ΔG均为负值,说明这7个异构化反应在理论上均可以自发形成,其中4(2)→1(2)的ΔG最小,说明异构化反应4(2)→1(2)最容易自发进行,而2(2)→1(4)的ΔG最大,说明异构化反应2(2)→1(4)较难进行.进一步观察发现,除反应2(2)→1(4)外,其他异构化反应均为熵减反应,说明团簇NiPS3异构转化反应趋向于减小系统的混乱度,生成更稳定的构型.值得关注的是,构型4(2)和构型1(2)均为平面五边形型构型,二者发生异构化反应4(2)→1(2)时反应常数K最大,可以从一定程度上说明平面型构型之间的转换更容易,反应更彻底. 分析各异构化反应的K值可以发现,反应4(4)→3(4)、2(2)→1(4)和5(4)→4(4)的K值小于105,说明这三个反应进行的不够彻底,反应物和生成物转化率相近,其他的异构化反应K值均大于105,正反应限度远大于逆反应限度,进行较为彻底.进一步分析发现,反应进行的限度与反应物和生成物之间相对能量的差值即反应物和反应物的稳定性差别有关:构型4(2)和构型1(2)的相对能量差最大,稳定性差别最大,K值最大,异构化反应进行的最为完全. 利用吉布斯-亥姆霍兹方程(ΔG=H-TΔS)分析可知,在异构化反应中,除反应2(2)→1(4)的ΔS大于0外,其他的异构化反应ΔS均小于0,所以对于这些反应来说,需要较低的温度来抵消ΔS小于0的影响,进而说明这些异构转化反应在低温下更加易于自发进行. 3.3.1团簇NiPS3异构化过程的活化能 过渡态理论认为反应物必须要吸收一定的能量,形成高能量活化络合物(过渡态)后,才能转化成生成物,此过程中吸收的能量被称为活化能Ea,活化能的大小可以反应异构化反应进行的难易程度.基于此,利用二次收敛自洽场(SCF)的方法,近似得出过渡态构型的总能量,通过反应物和过渡态能量,进而求出正逆反应活化能的大小列于表3,其中EaF表示异构化反应正向进行时的活化能,EaB表示异构化反应逆向进行时的活化能. 表3 团簇NiPS3异构化反应的总能量及活化能 活化能越小,活化分子数越多,说明该反应越容易进行,观察表3的数据,可以发现,所有异构化反应的EaF均小于EaB,说明在所有的异构化反应中正向反应均比逆向反应容易进行,即能量高的构型向能量低的构型转换更容易. 单分子反应完成97%时需要的反应时间遵循以下关系式: t=-(ln0.03)/K (2) 其中K=2.1×1010×T×e-1000ΔE/(1.9859×T),表示反应速率常数,ΔE表示反应活化能.由上式可求得,在常温常压下,当异构化反应的活化能为88 kJ·mol-1时,所需要的反应时间为22.3 min,活化能为92 kJ·mol-1时,所需要的反应时间为2 h.因此,当过渡态的活化能小于88 kJ·mol-1时,可以认为该反应在常温常压下能够正常进行,反之则较难正常进行.据此并结合异构化反应的平衡常数分析可得:对于生成1(2)的反应4(4)→1(2)、3(2)→1(2)和4(2)→1(2)而言,其正反应的活化能均小于88 kJ·mol-1,且异构化反应的平衡常数分别为2.383×1014、8.381×108和1.208×1019远大于105,所以这3个异构化反应在常温下容易进行且进行程度非常大,其逆反应的活化能均大于88 kJ·mol-1,导致逆反应在常温下很难发生,因此这3个反应几乎只有正反应进行,说明构型4(4)、3(2)和4(2)不能稳定存在,会迅速转化为构型1(2),构型1(2)能量最低,相对来说较为稳定. 为了更直观的展现团簇NiPS3构型间异构转化过程中能量的变化和连串反应情况,依据表3中的相关数据绘制出如图3所示的反应能垒图.观察图3,可以发现在常温常压下,团簇NiPS3通过5个不同的异构转化途径最终转化为构型1(2)、3(4)和构型1(4),途径如下:(Ⅰ)4(2)→1(2);(Ⅱ)3(2)→1(2);(Ⅲ)5(4)→4(4)→1(2);(Ⅳ)5(4)→4(4)→3(4);(Ⅴ)5(4)→2(2)→1(4) 图3 团簇NiPS3异构化反应的能垒图 结合异构化反应的平衡常数、正逆反应的活化能对以上5个异构转化途径进行讨论:对于途径Ⅰ而言,反应4(2)→1(2)的K值远大于105,且EaF小于88 kJ·mol-1,EaB大于88 kJ·mol-1,说明构型4(2)不能稳定存在,会迅速转化为可以稳定存在的构型1(2);对于途径Ⅱ而言,反应3(2)→1(2)的K值大于105,且EaF小于88 kJ·mol-1,EaB大于88 kJ·mol-1,说明构型3(2)不能稳定存在,会迅速转化为可以稳定存在的构型1(2);对于途径Ⅲ和Ⅳ,后半段构型4(4)参与生成构型1(2)和构型3(4),为平行反应,存在主副反应的竞争,反应4(4)→1(2)的K值(2.383×1014)远大于反应4(4)→3(4)的K值(1.638×101),且前者的EaF远低于后者,所以在此平行反应中,反应4(4)→1(2)为主反应,构型3(4)的生成极少,前半段均为反应5(4)→4(4),虽然K值位于10-5~105之间,正逆反应速率相同,但是由于构型4(4)参与生成构型1(2),一直在被消耗,所以构型5(4)也不能稳定存在;对于途径Ⅴ而言,反应5(4)→2(2)的K值为大于105,且其EaF远大于EaB,说明构型5(4)不能稳定存在,易于转化为构型2(2),而反应2(2)→1(4)K值为小于105,且其EaF与EaB大小相近,说明构型2(2)和构型1(4)相互转化的速率相同,即均可稳定存在.综上所述,在常温常压下,构型1(2)、构型2(2)和构型1(4)可以稳定存在,而其他构型则会通过异构化反应转化为构型构型1(2)、构型2(2)和构型1(4). 3.3.2团簇NiPS3异构化反应的反应速率及平衡常数 为了从化学动力学对团簇NiPS3异构化反应进行进一步的分析,利用过渡态理论计算出团簇NiPS3各异构化反应的正、逆反应速率常数和化学平衡常数K,其计算方法如下: k(T)=κ(T)kTST (3) K=kaF/kaB (4) 其中k(T)是过渡态反应过程中正、逆反应的实际速率常数,kTST为理论计算的速率常数,к(T)为魏格纳校正系数. 反应速率常数的大小决定化学反应进行的快慢,观察表4可知,各异构化反应的正反应速率常数均大于逆反应速率常数,说明团簇NiPS3各异构转化反应均以正反应方向为主,这与分析团簇NiPS3异构化活化能得出的结论一致.观察反应平衡常数K的值,也可以发现反应4(2)→1(2)、反应3(2)→1(2)、反应4(2)→1(2)和反应5(2)→2(2)的K值均大于105,且反应反应2(2)→1(4)的K值近似为1,构型2(2)和构型1(4)相互转化速率相同,说明构型1(2)、构型2(2)和构型1(4)可以稳定存在,也验证了分析反应能垒图得出的结论. 表4 团簇NiPS3异构化反应的反应速率常数和动力学平衡常数 对比表2和表4的平衡常数K的大小,可以发现从化学热力学角度和化学动力学角度,对K值进行计算,二者所得出的值在数量级上基本一致(仅存在0~1个数量级的变化),说明从化学热力学角度和化学动力学对团簇NiPS3异构转化反应进行分析,所得到关于反应限度的结论基本一致. 本文依据拓扑学原理,利用密度泛函理论,对团簇NiPS3进行优化分析,得出7种过渡态构型,根据过渡态理论,从热力学和动力学两个角度出发,对团簇NiPS3的异构转化反应进行研究,最终得到了以下结论: 1)过渡态的几何形态全为立体构型,且以三角双锥型构型为主,仅TS5(4)→1(2)为四棱锥. 2)通过对过渡态构型的成断键进行分析发现,过渡态构型的稳定存在依赖于非金属-金属和非金属-非金属之间的成键与断键. 3)在异构化反应中,反应限度较小,反应物和产物之间稳定性差别越大,反应进行的越彻底,反应2(2)→1(4)、反应2(2)→1(4)和反应2(2)→1(4)进行的不够彻底;除反应2(2)→1(4)外,其他的异构化反应在低温下更加易于自发进行. 4)团簇NiPS3异构转化反应趋向于减小系统的混乱度,且正反应活化能均小于逆反应活化能,正反应速率均大于逆反应速率,说明这些异构化反应均趋向于正向进行,生成更稳定的构型,即能量高的构型向能量低的构型转换更容易. 5)构型1(2)、构型2(2)和构型1(4)可以稳定存在,是团簇NiPS3异构转化的最终产物,在进行相关材料的研究、开发和生产时,可优先考虑.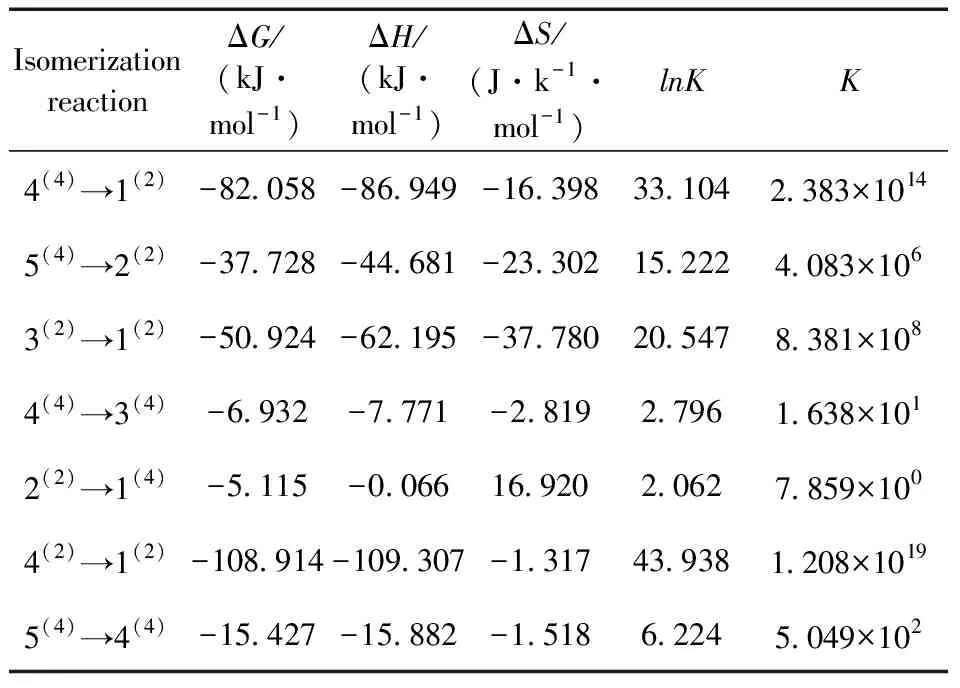
3.3 团簇NiPS3异构化的动力学分析


4 结 论

