Lu-Eu共掺杂Ga2O3的光电性质的第一性原理计算

邹梦真, 肖清泉, 姚云美, 付莎莎, 叶建峰, 唐华著, 谢 泉

(贵州大学 大数据与信息工程学院新型光电子材料与技术研究所, 贵阳 550025)

1 引 言

第四代半导体材料中，由于氮化铝(AlN)和金刚石仍面临大量科学问题亟待解决，氧化镓则成为继碳化硅(SiC)和氮化镓(GaN)之后最具市场潜力的材料. 氧化镓有5种同分异构体，分别为α、β、γ、ε和δ. α- Ga2O3属于三方晶系，它是刚玉晶体结构. γ- Ga2O3和δ- Ga2O3属于立方晶系，δ- Ga2O3为方铁锰矿结构，ε-Ga2O3属于六角晶系. Ga2O3的五种同分异构体中，β-Ga2O3是目前为止研究最多的同分异构体，因为β相氧化镓最为稳定，当加热至1000 ℃或湿法加热至300 ℃以上时，其他所有亚稳相的异构体都会被转换为β相异构体[1]. β-Ga2O3有优越的透明度、热稳定性[2，3]、生产成本低[4]等优点，近年来被科研人员大量研究[5].

Sun等人[6]发现从能量角度看，O原子比Ga原子更容易脱离晶格位置，从而形成氧空位. β-Ga2O3由于O空位的存在而呈现出n型半导体的特征[7]，目前n型半导体已经基本实现[8]利用这一特点已将其广泛用于制备传感器、紫外光电探测器和大功率电子器件[9，10]. 2019年He 等人实验制备了基于石墨烯/β-Ga2O3/GaN异质结探测器[11]，光响应度达到550 A/W. 2020年，Feng等人[12]在铁掺杂半绝缘β-Ga2O3衬底上外延生长了UID缓冲层和锡掺杂外延层并实现了具有较高饱和电流的新型增强型MOSFET. β-Ga2O3的带隙变化范围为4.2 eV到4.9 eV[13]，带隙比GaN(3.4 eV)和SiC(3.2 eV)的都要大. β-Ga2O3存在优异p型导电材料难以制备的问题[14-16]，对β-Ga2O3器件的发展有所限制. 2020年，Ma等人[17]对β-Ga2O3进行Al-N和In-N掺杂，发现Al-N掺杂比N单掺更易产生更浅的跃迁能级. 2018年，Su等人[18]研究了β-Ga2O3中掺杂Zn和Mg，发现掺杂会引入受主能级，但受主能级的位置相对比较深，再次反映了P型掺杂β-Ga2O3的实现具有一定的困难. 调控材料性能可以采用压力调控[19]和界面工程[20]，也可通过掺杂提高基于β-Ga2O3的器件的性能[21-24]. 本文将采用基于DFT的第一性原理方法，对Lu掺杂浓度为12.5%的β-Ga2O3体系以及Lu-Eu共掺杂浓度为25%的β-Ga2O3体系的光学性质以及电子结构进行探索. 为后续的理论研究以及实验制备提供一定的理论参考.

2 计算方法

β-Ga2O3是单斜晶系，所属空间群为C2/m，其晶格常数a=12.25 Å，b=3.04 Å，c=5.80 Å，夹角β=103.7°[25]. 本文采用有20个原子的β-Ga2O3的单胞结构作为计算的基本单元，如图1(a)所示. 用一个Lu原子替换图1(a)中的一个Ga原子，得到Lu掺杂浓度为12.5%的β-Ga2O3结构如图1(b)所示，用一个Eu原子替换图1(b)中的一个Ga原子，得到Lu-Eu共掺杂浓度为25%的β-Ga2O3结构如图1(c)所示. 本文的计算都基于密度泛函理论的Cambridge Sequential Total Energy Package(CASTEP)软件包完成，分别采用了PBE(Perdew-Burke-Ernzerhof)中的GGA(Generalized Gradient Approximation)和GGA+U(Generalized Gradient Approximation-Hubbard U)的方法进行计算. 计算时本征β-Ga2O3结构，Lu掺杂β-Ga2O3结构以及Lu-Eu共掺杂的β-Ga2O3结构的优化参数设置相同，原子最大位移收敛标准0.001Å、原子间最大相互作用力设置为0.02 eV/Å、自洽精度设为2.0×10-5eV/atom、原子上的最小作用力0.05 GPa、截断能设置为570 eV、 k采样密度设置为2×8×4. 对β-Ga2O3进行几何优化，结构优化完成的标志是4个参数均达到或优于收敛标准.

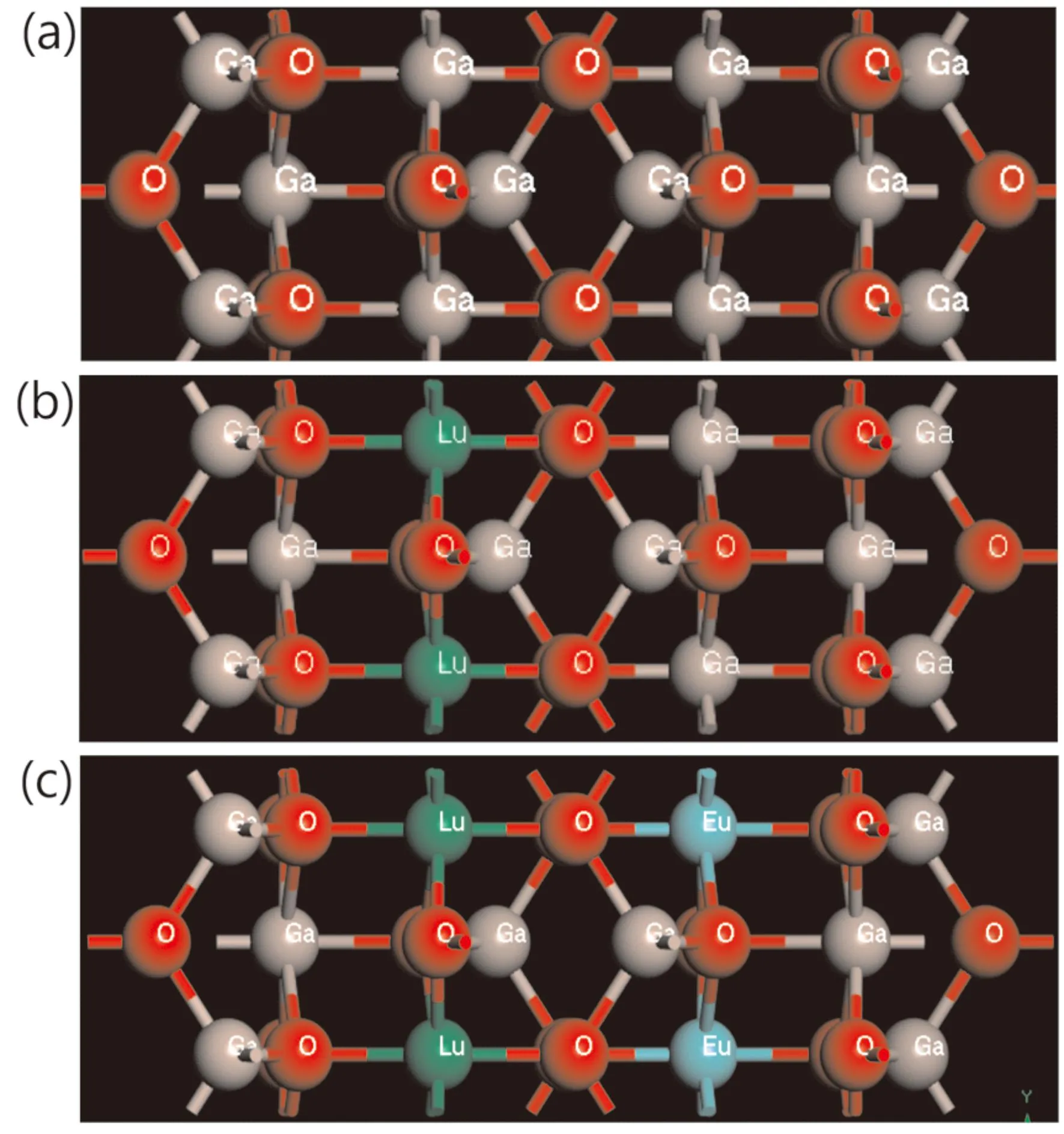
图1 (a)本征β-Ga2O3结构；(b)Lu掺杂的β-Ga2O3结构；(c)Lu-Eu共掺杂β-Ga2O3结构Fig. 1 The structures of (a)intrinsic β-Ga2O3 ，(b)Lu-doped β-Ga2O3 ，and(c)Lu-Eu co-doped β-Ga2O3

3 结果与分析

3.1 几何优化结果分析

表1中包含了采用PBE中的GGA和GGA+U的方法计算本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3结构的晶格常数和体系总能量. 由表1可知本征β-Ga2O3用GGA+U的方法计算得到的晶格常数a、b、c的值分别是12.45 Å、3.08 Å以及5.88 Å，与文献值基本一致[25]，表明优化的参数设置较合理，后续模拟计算结果有一定的准确性. 由表1可以看出Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3体系的总能量小于本征β-Ga2O3，也即掺杂后的β-Ga2O3结构可能会更稳定. 采用GGA方法计算三个体系得出的晶格常数值是随着掺杂元素的增多而变大. 对比GGA和GGA+U的方法计算的三个体系的晶格常数，可以看出GGA+U计算的晶格常数都略小于GGA方法计算所得晶格常数.

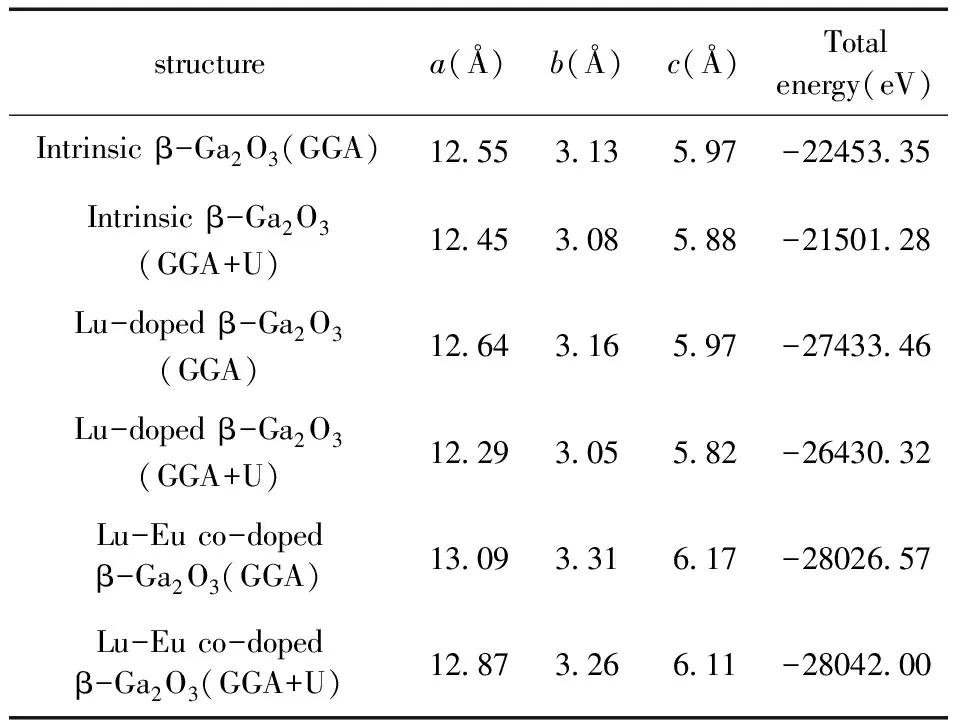
表1 本征β-Ga2O3，Lu掺杂β-Ga2O3以及Lu-Eu共掺杂的β-Ga2O3结构晶格常数和体系总能量

3.2 电子结构

3.2.1能带结构

图2展示了用GGA和GGA+U的方法计算本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3得到的能带结构图. 从图2(a)中可以看出用GGA方法计算的本征β-Ga2O3的带隙值为1.72 eV，图2(b)则是用GGA+U的方法计算本征β-Ga2O3得到的能带结构图，由图2(b)得知本征β-Ga2O3的带隙值为4.24 eV，这与实验值4.4 eV[25]相差不大. 图2(c)和(d)分别表示了用GGA和GGA+U方法计算Lu掺杂浓度为12.5%的β-Ga2O3结构得到的能带图，由图2(c)和(d)可知Lu掺杂浓度为12.5%的β-Ga2O3的带隙值分别为2.02 eV和2.23 eV. Lu-Eu共掺杂浓度为25%的β-Ga2O3的能带结构如图2(e)和(f)所示，由图2(e)可以得知GGA方法计算的带隙值为0.45 eV，由图2(f)可以得知GGA+U方法计算的带隙值为0.90 eV. 对比三个体系分别用GGA和GGA+U的方法计算得到的带隙值，可以发现GGA+U方法计算的带隙值大于GGA方法计算的，对于本征β-Ga2O3结构，GGA+U方法计算的带隙值几乎接近实验值，表明GGA+U方法修正了GGA方法中由于DFT(Density Functional Theory)对电子的交换关联势低估造成的误差. 因此，对能带结构图的分析侧重于采用GGA+U方法计算所得的图2(b)、(d)和(f).

从图2(b)可以得知本征β-Ga2O3为直接带隙半导体材料，导带底和价带顶均位于布区的G处. 图2(d)展示了Lu掺杂浓度为12.5%的β-Ga2O3的能带结构图，其导带底和价带顶均位于布区的G处，由图可以看出Lu掺杂后β-Ga2O3的带隙值为2.23 eV，带隙明显减小，由于Lu掺杂浓度为12.5%的β-Ga2O3的费米能级向下进入价带故为P型掺杂. 图2(f)展示了Lu-Eu共掺杂浓度为25%的β-Ga2O3的能带结构图，其导带底和价带顶均位于布区的Q处，由图可以看出Lu-Eu共掺杂后β-Ga2O3的带隙值为0.9 eV，带隙明显减小. 由图2(d)和(f)可以看出，Lu掺杂和Lu-Eu共掺杂后β-Ga2O3依旧是直接带隙材料，但掺杂使得β-Ga2O3的带隙值减小. 推测禁带宽度变小的原因是：Lu和Eu原子最外层电子数是2，而Ga原子最外层电子数为3，Lu和Eu最外层电子比Ga最外层少了1个，受到Lu掺杂和Lu-Eu共掺杂的影响，改变了费米面附近电子结构，使导带向低能方向偏移，价带向高能方向偏移，禁带宽度变窄.

3.2.2态密度

本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3结构的总态密度(TDOS)和分态密度(PDOS)如图3所示. 图3(a)是本征β-Ga2O3在-10 eV-20 eV能量范围内的TDOS和PDOS，由图3(a)可知，本征β-Ga2O3的价带主要由O-p态和少量Ga-s态组成，导带部分主要由Ga-s态和少量O-p态占据. 对本征β-Ga2O3，可将总态密度图可以分为三个能量区间进行分析讨论. 在-10 eV-0 eV时，β-Ga2O3的总态密度主要是来自于O的p轨道；在0 eV-10 eV时，对总态密度的主要贡献是Ga-s态；在10 eV-20 eV时，对β-Ga2O3的总态密度的贡献主要来自于Ga的p态和O的s态.

图3 各掺杂体系的态密度：(a)本征β-Ga2O3 ；(b)Lu掺杂的β-Ga2O3；(c)Lu-Eu共掺的β-Ga2O3Fig. 3 Densities of states of various doping β-Ga2O3 systems：(a)Intrinsic β-Ga2O3；(b)Lu-doped β-Ga2O3；(c)Lu-Eu co-doped β-Ga2O3

图3(b)是Lu掺杂浓度为12.5%的β-Ga2O3在-20 eV—20 eV能量范围内的TDOS和PDOS，由图3(b)可知，Lu掺杂β-Ga2O3导带部分主要由Ga-s态、Ga-p态、O-p态、Lu-d态以及少量O-s态构成，而其价带部分主要由O-p态、O-s态、Ga-d态和Lu-f态构成. 对Lu掺杂浓度为12.5%的β-Ga2O3的总态密度图分三个能量区间进行讨论，在-20 eV—-10 eV时，Lu掺杂后β-Ga2O3的总态密度主要来自Ga-d态和O-s态；在-10 eV—0 eV时，Lu掺杂后β-Ga2O3的总态密度主要来自O-p态和少量Lu-f态；在0 eV—20 eV内，对总态密度的主要贡献是Lu的d态、Ga-p态和O-p态. 和未掺杂β-Ga2O3对比，Lu掺杂浓度为12.5%的β-Ga2O3体系禁带变窄，这与能带图的分析一致. 图3(c)是Lu-Eu共掺杂浓度为25%的β-Ga2O3在-15 eV—30 eV能量范围内的TDOS和PDOS，由图3(c)可知，Lu-Eu共掺β-Ga2O3的导带部分主要由Eu-f态、Lu-p态以及少量的Ga-p态和O-p态构成，其价带部分则主要由O-p态、Lu-p态、Eu-f态构成. 对Lu-Eu共掺杂β-Ga2O3的总态密度图也分三个能量区间进行讨论，在-15 eV—-10 eV时，Ga-d态和Lu-d态以及少量O-s态对总态密度贡献较多；在-10 eV—0 eV时，对总态密度的主要贡献是O-p态和Eu的f态；而在0 eV—30 eV时，对总态密度的主要贡献是Eu-f态、Eu-d态、Lu-f态以及少量的Lu-p态、O-p态和Ga-p态. 和Lu掺杂β-Ga2O3对比，Lu-Eu共掺杂β-Ga2O3后体系使得价带向高能方向移动，导带向低能方向偏移，禁带变的更窄. 对态密度的分析与能带图的分析相符合.

3.3 光学性质

3.3.1介电函数

本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3的复介电常数如图4所示，图4(a)为本征β-Ga2O3，Lu掺杂β-Ga2O3以及Lu-Eu共掺杂的β-Ga2O3介电函数实部图像，由图可知本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3在能量零点的静态介电常数分别是是3.12、3.36、3.33. 且分别在光子能量为7.92 eV、7.5 eV、7.16 eV时取得各自峰值4.01、4.38、4.45.另外，在0 eV—8 eV的光子能量范围内，Lu掺杂和Lu-Eu共掺后β-Ga2O3的介电常数值略大于本征β-Ga2O3的介电常数值，说明在光子能量0 eV—8 eV范围内对电荷的束缚能力变强. Lu-Eu共掺杂β-Ga2O3的介电函数的实部在8 eV—15 eV范围内略小于本征和Lu掺杂体系；在15 eV—25 eV范围内又略大于本征和Lu掺杂体系；在25 eV—50 eV范围内，介电函数的实部逐渐减小.

图4 各掺杂体系的复介电常数：(a)介电常数实部；(b)介电常数虚部Fig. 4 Dielectric functions of various doping β-Ga2O3 systems：(a)Real parts；(b)Imaginary parts

图4(b)为本征β-Ga2O3，Lu掺杂β-Ga2O3以及Lu-Eu共掺杂的β-Ga2O3的介电函数虚部图像，由图可知本征β-Ga2O3的峰值是3.28位于15.6 eV处，在能量11.5 eV时取得次峰值2.92. 出现该波峰的主要原因是Ga-s态电子和O-p电子的跃迁. Lu掺杂后β-Ga2O3在光子能量15.3 eV时取得峰值3.5，在能量12.03 eV时取得次峰值3.26. 在0 eV—16 eV的光子能量范围内，Lu掺杂浓度为12.5%的β-Ga2O3的介电常数值略大于本征β-Ga2O3的介电常数值，表明了掺杂使得β-Ga2O3在低能区的光跃迁强度增加. Lu-Eu共掺杂的β-Ga2O3在光子能量12 eV取得峰值3.58，在能量9.19 eV处取得次峰值3.04，在0 eV—13 eV的光子能量范围内，Lu-Eu共掺体系的介电常数值略大于本征和Lu掺杂体系，表明了Lu-Eu共掺使得β-Ga2O3在低能区的电子吸收光子的可能性变大，激发态的电子变多，光跃迁强度明显增加.

3.3.2吸收谱

本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3的吸收谱如图5所示. 由图可得本征β-Ga2O3的吸收系数的峰值和次峰值分别在18.7 eV和16.3 eV处取得，其值分别为3.3×105cm-1和3×105cm-1. Lu掺后β-Ga2O3的吸收系数在19.4 eV处取得峰值3.15×105cm-1，Lu-Eu共掺杂的β-Ga2O3的吸收系数在25.8 eV处取得次峰值2.47×105cm-1，在31.7 eV处取得峰值2.54×105cm-1. 计算结果表明在低能区0 eV—14 eV范围内，Lu-Eu掺杂后体系的吸收系数比本征β-Ga2O3和Lu掺后β-Ga2O3的略大；在14 eV—25 eV能量范围内，本征β-Ga2O3和Lu掺杂后的体系的吸收系数则高于Lu-Eu共掺β-Ga2O3体系；在25 eV—60 eV能量范围内，Lu掺杂后的体系和Lu-Eu共掺β-Ga2O3体系的吸收系数则高于本征β-Ga2O3体系，这表明了掺杂提高β-Ga2O3在高能区的吸收能力.

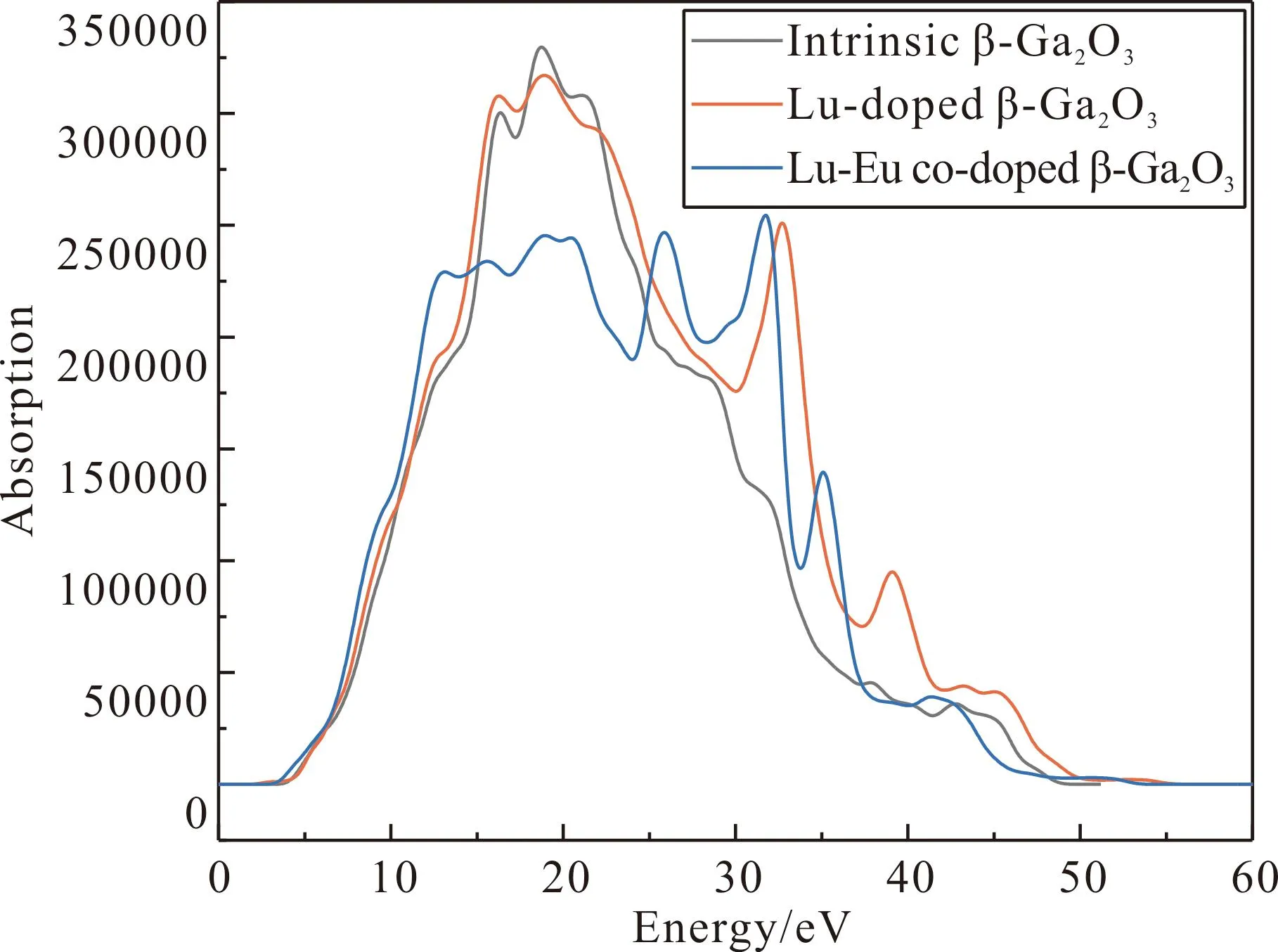
图5 各掺杂体系的吸收系数Fig. 5 Asorption coefficients of various doping β-Ga2O3 systems

3.3.3反射系数

本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3体系的反射系数如图6所示. 从图中可以看出本征β-Ga2O3在能量为0 eV时反射率为0.077，其反射率具有三个明显的峰，在22.2 eV处达到最高峰值0.237，最高峰后随着能量的增加，本征β-Ga2O3的反射系数逐渐减小. Lu掺杂β-Ga2O3体系在能量为0 eV处的反射率为0.087. Lu掺后β-Ga2O3的反射系数在16.2 eV处取得峰值0.22，然后在能量范围为30 eV—33.8 eV时，反射系数随着光子能量的增大而增大，然后在33.8 eV后逐渐减小. Lu-Eu共掺杂的β-Ga2O3在能量为0 eV时的反射率为0.085，其反射率有两个明显的峰，在12.5 eV处取得峰值0.197，在32.4 eV处取得次峰值0.17. 对比本征β-Ga2O3，Lu掺杂β-Ga2O3以及Lu-Eu共掺杂的β-Ga2O3三个体系在能量为0 eV时的反射率，可以得出Lu掺杂β-Ga2O3以及Lu-Eu共掺杂的反射率均大于本征β-Ga2O3的反射率，这表明着Lu元素以及Eu元素的掺杂使β-Ga2O3在能量为0 eV时的透射能力变弱. 计算结果表明在低能区0 eV—15 eV范围内Lu-Eu共掺杂后体系的反射系数略大于本征β-Ga2O3和Lu掺杂β-Ga2O3. 本征β-Ga2O3在取得峰值后，随着能量的增加，其反射率是逐渐减小的；而Lu掺杂β-Ga2O3和Lu-Eu共掺杂β-Ga2O3则是在33.8 eV和32.5 eV处各自取得次峰值后，随着能量的增大其反射率整体下降. Lu-Eu掺杂体系的反射率在能量为15 eV—25 eV时，与本征及Lu掺杂体系相比，其反射率明显降低. Lu掺杂和Lu-Eu掺杂体系的反射率峰值均低于本征β-Ga2O3，表明掺杂使得β-Ga2O3对可见光的利用率增强.

图6 各掺杂体系的反射率Fig. 6 Reflectivity coefficients of various doping β-Ga2O3 systems

4 结 论

本文先采用PBE中的GGA和GGA+U的方法计算了本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3结构的晶格常数、能带结构和体系总能量. 发现采用GGA+U的方法计算的带隙值更接近实验值，也即计算更精确. 然后采用GGA+U的方法计算了本征β-Ga2O3，Lu掺杂浓度为12.5%的β-Ga2O3以及Lu-Eu共掺杂浓度为25%的β-Ga2O3结构的态密度、介电函数、吸收谱以及反射率等基本物理特性. 计算结果表明本征β-Ga2O3的带隙为4.24 eV，是直接带隙半导体材料，Lu掺杂浓度为12.5%的β-Ga2O3的带隙为2.23 eV，仍为直接带隙半导体材料. Lu原子在β-Ga2O3属于受主杂质，在β-Ga2O3中引入的深受主杂质成为有效的复合中心. Lu-Eu共掺杂浓度为25%的β-Ga2O3的带隙为0.9 eV，仍为直接带隙半导体材料. 此外，光学性质的计算结果表明，在低能区内掺杂体系的介电函数、反射率和吸收系数均强于本征β-Ga2O3，表明Lu掺杂和Lu-Eu共掺杂改善了本征β-Ga2O3在红外光区的光电性能，有望应用于制作红外光电子器件.