雷达地形遮挡盲区的大气折射修正算法
李冠运,刘松涛,徐华志
(1.中国人民解放军92011部队,上海 202150;2.海军大连舰艇学院信息系统系,辽宁 大连 116018)
0 引言
地形遮蔽盲区的计算是雷达威力研究的重要内容。由于地形遮挡对雷达中低空探测产生的影响是基础且广泛的[1],研究雷达地形遮蔽盲区能够为雷达选址、预警组网、低空突防等提供现实支撑,具有很好的研究应用价值。
目前,地理信息系统(GIS)技术的发展与应用为量化评估地形遮蔽对雷达探测造成的影响提供了研究条件,但目前的相关结合性应用研究多依赖GIS技术的通视分析功能,主要有基于视线的方法、基于并行计算系统的可视性分析模型、利用邻近视点之间的内在一致性改进并行算法、基于斜率比较的可视性算法等[2]。然而,地形遮蔽条件下的雷达探测能力分析并不完全等同于通视分析,若直接套用相关算法将导致以下两个问题。
一是计算结果不精确。通视分析相关算法多聚焦计算效率和准确性的提升,往往不考虑大气折射误差的修正。然而对于雷达探测来说,大气折射将导致雷达波束弯曲,显著影响遮蔽盲区的计算,若直接套用通视算法而不修正大气折射,将导致计算出现严重误差。但是对相关误差的修正研究并不多见。
二是计算产品的适用性不强。通视分析多聚焦于观察点与地表或某高度层的可视分析,形成的产品多为可视域。文献[3]即是在通视分析的基础上,求解地形遮挡条件下的地表电磁波覆盖范围,并运用等效地球法对结果进行了修正。
不同于以上研究,本文所聚焦的是地表以上的全空域分析,目的是对雷达威力边界进行定位,计算产品更具有普适性和实时性。本文提出运用等效地球半径法和二元曲率方程法来计算雷达地形遮蔽时的大气折射误差,可以有效地提升雷达地形遮蔽盲区的建模精度和计算产品的适用性。
1 大气折射对雷达地形遮蔽盲区计算的影响
在雷达探测领域,针对大气折射导致的测角、测距、测速等误差修正[4-5],已经形成了较为成熟的方法。文献[6]对射线描迹法、线性分层法和等效地球半径法等误差修正方法在多种场景下的具体应用进行了详细说明。文献[7]提出了利用差分方法求解任意大气层中的射线规范方程,并对单脉冲雷达和三基地雷达进行了实用的误差修正。文献[8]对各类算法的使用范围及优缺点进行了分析,并给出了雷达系统大气折射误差修正技术在今后的研究方向。文献[9]为解决误差修正的精确性与实时性矛盾提供了思路。本文借鉴以上解算方法,研究雷达地形遮挡盲区受大气折射的影响情况。
雷达地形遮蔽盲区是指在地形遮挡的作用下,雷达能量无法实现空间上的全面覆盖,导致在雷达探测范围内产生的不可探测空间域,如图1所示。
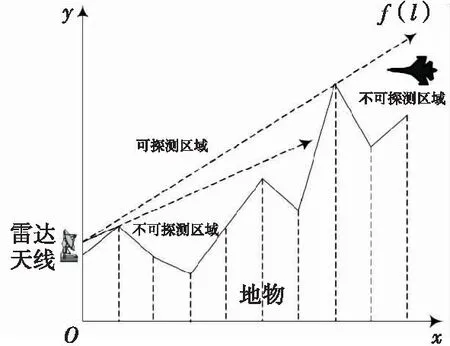
图1 地形遮挡导致的雷达探测盲区Fig.1 Radar detection blind spots due to terrain occlusion
若不考虑Fresnel区影响,地物遮挡导致雷达威力范围在三维空间中存在边界,边界以下为地形遮蔽盲区。计算雷达遮蔽盲区的本质即是求解该边界,以角度为切分,该边界应是以雷达距离l为变量的高度函数,记为f(l)。
在无线电领域,大气折射通常指由于地球大气层折射指数n在垂直梯度上的变化,造成无线电波传播射线变得弯曲的现象。大气折射计算出发点通常是Snell定律,以雷达为例,它表示为
nrcosθ=n0r0cosθ0=常数,
(1)
式(1)中,θ0和θ分别为射线初始仰角和射线仰角,n和n0分别为地面和空中折射指数,r和r0分别为雷达和目标到地心距离。定义e0为射线上某点切线指向角对弧长的变化率,曲率半径ρ=1/e0,根据式(1)有ρ=1/e0=-n/[cosθ(dn/dh)],考虑到n≈1,可见折射指数垂直梯度dn/dh越大,射线曲率半径ρ就越小,射线弯曲就越明显[10]。大气折射对计算雷达地形遮挡盲区造成的影响如图2所示。
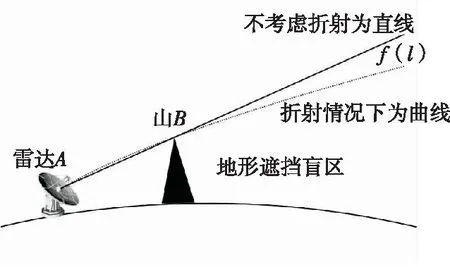
图2 大气折射对雷达地形遮挡盲区造成的影响Fig.2 The effect of atmospheric refraction on the blind spot caused by radar terrain occlusion
图2中,雷达A波束被山B遮挡,形成了威力边界f(l),由图中不难看出,受大气折射影响,f(l)向地心方向弯曲,导致雷达探测盲区高度降低。该误差会随着雷达作用距离l增大而快速提升,使求解结果严重失真,如图3所示。因此,对大气折射的修正是求解雷达地形遮挡盲区关键环节。
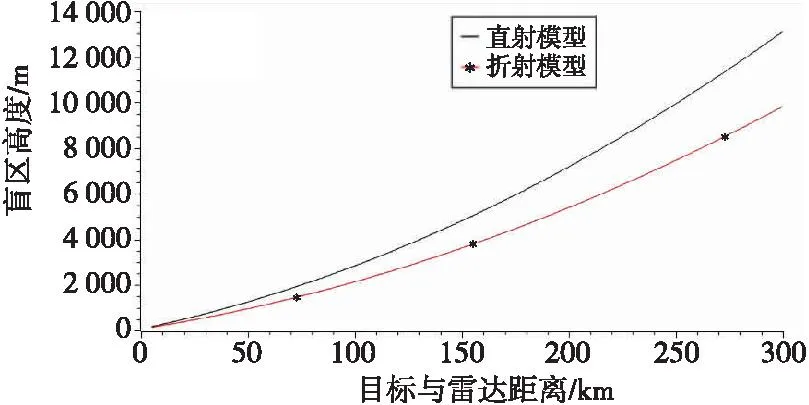
图3 雷达地形遮挡盲区高度随雷达作用距离变化的示意图Fig.3 Schematic of the variation of radar terrain occlusion blind spot height with radar action distance
2 基于等效地球半径的大气折射修正算法
2.1 求解思路
等效地球半径法是在一定条件下,将实际地球半径以某种等效地球半径替代,从而使大气等效为均匀,实现化曲为直,简化计算目的,在工程上得到广泛引用。关于等效地球半径法推导过程,文献[10-11]均有较为细致阐明,在此不做赘述。等效地球半径法修正大气折射是在雷达威力边界计算中引入了基于等效地球半径的电磁波传播模型来实现,下面以实例简要介绍该方法的应用。
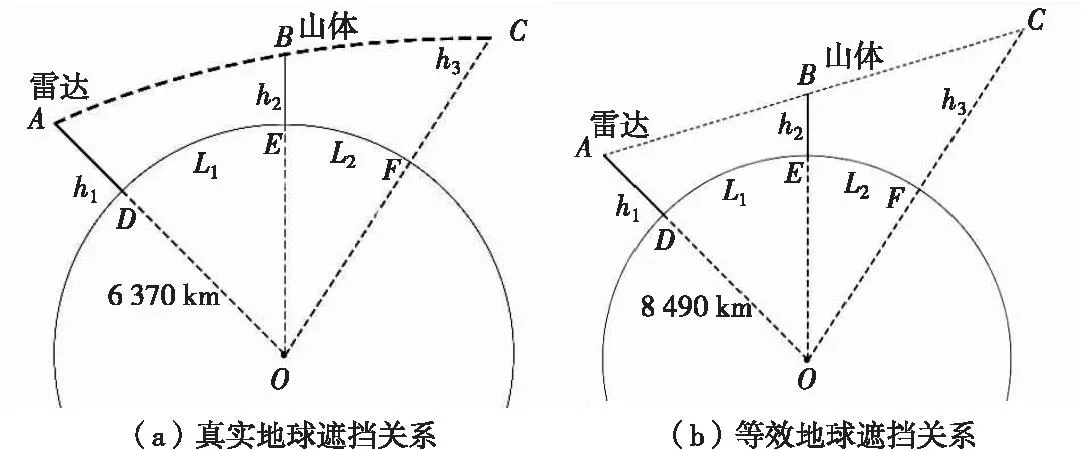
图4 遮挡关系示意图Fig.4 Schematic diagram of shading relationship
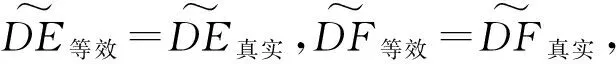
2.2 主要问题及解决方法
2.2.1初始仰角θ0可能引起的误差
关于等效地球半径法的概念定义和局限性问题,文献[11-12,14]做了讨论,但对于起始仰角θ0≈0是否为该方法的充分必要条件,给出了不同意见。文献[11]以等效地球中相对曲率必须保持不变为依据,得出了θ0≈0是等效地区半径法充分必要条件;文献[12]从大气折射指数梯度近似角度出发,认为θ0取值不影响等效地球半径法的适用;文献[14]则认为该问题主要取决于等效地球半径法定义方法,若以相对曲率等效法来看θ0≈0是必须的,但若以折射梯度效应等效法来推导,θ0取值与方法的使用基本无关。本文通过数据计算的方式检验证明,运用等效地球半径法计算雷达地形遮蔽盲区这一工程应用中,θ0≈0并不是等效地球法的限制条件。
2.2.2大气折射梯度的非线性变化可能引起的误差
等效地球半径法的定义是基于均匀球面分层且折射指数垂直梯度不随高度变化(dn/dh为常数)的大气环境[11]。根据文献[10],在近地0~1 km高度范围内,dn/dh呈线性分布,4/3等效地球半径法精度较高,但高于1 km后dn/dh为负指数分布,导致等效地球半径法出现误差,而防空雷达地形遮挡盲区高度往往超过了这一数值。针对以上不足,在文献[13]的基础上,本文提出一种多层等效地球半径法,实现对误差的进一步修正。
1) 确定多层等效地球半径
根据文献[10],地面至60 km高度范围中,较为科学的大气折射描述方法应为分段模型,即海拔高度h处的折射率N(h)为
(2)
式(2)中,N0为地面折射率,h0为地面海拔,ΔN1是0~1 km折射变化率(标准大气下是39 N/km),N1是海拔1 km折射率,Ca1为地面上空1~9 km指数衰减系数,N9是海拔9 km折射率(该值一般稳定在105 N),Ca9为地面上空9~60 km指数衰减系数(每千米年平均衰减系数为0.143 2)。
因大气环境的差异,N0,ΔN1,Ca1在不同地区、不同时段取值均有不同,在计算时可参考各地区统计数据。在此以北京地区7月份平均统计数据为例,取N0=369 N,ΔN1=51 N/km,Ca1=0.14,绘制1~9 km和9~20 km负指数函数图像,见图5。
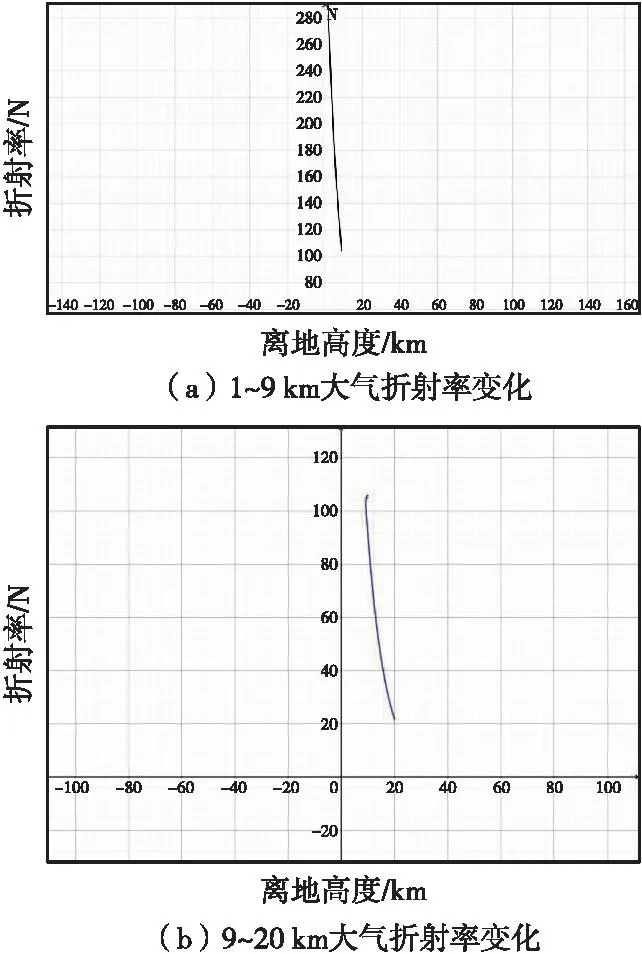
图5 北京地区7月份1~20 km大气折射率变化情况图Fig.5 Changes in atmospheric refractive index in Beijing from January to July
图5中,N(h)在1~20 km区间函数形态仍保留较强线性特征,若将其近似为线性函数,可实现在高空域使用等效地球法的目的,大大简化复杂运算而付出较小的精度代价。根据计算,1~9 km平均ΔN=27 N/km;9~20 km平均ΔN≈7.5 N/km。
根据等效地球半径系数的计算公式:
(3)
得到k1~9≈1.21,k9~12≈1.05,对应的等效地球半径分别为a1=7 708 km,a2=6 689 km。通过在0~1 km,1~9 km,9~20 km空域分别使ae等于8 490 km,7 708 km和6 689 km,即可实现分级修正。
2) 具体算例
假设雷达A架设高度h1=72 m,在某方向上受到山B遮挡,山B与雷达A相距为L2=15.14 km,山B高度h2=222 m,见图6,求解其400 km外的C点地形遮蔽盲区高度h3。

图6 算例遮挡关系图Fig.6 Arithmetic masking relationship diagram
首先取ae=8 490 km做等效地球变换,则有图7所示遮挡关系。

图7 算例第一层遮挡关系图Fig.7 Image of the first layer of occlusion relations of the algorithm
假定存在G点海拔为1 000 m,根据几何换算关系,可反推出G点与雷达A的地表投影距离为70.5 km,G点与C点地表距离为329.5 km,h3=13 118 m。以G点为起点,ae=7 708 km,做第二层等效地球转化,在此最困难的是确定转换后的几何关系,解决方法是参考第一次转化,几何关系的确定是依赖山B的“锚点”作用,因此在第二层转化前,要先找到G点的“锚点”。假设距离G点地表距离100 km存在高度为h4的山H,其对G点的遮挡刚好在C点达到13 118 m,根据几何关系,h4=3 322 m,则第二层等效地球转化可基于山H对G点的遮挡,见图8。
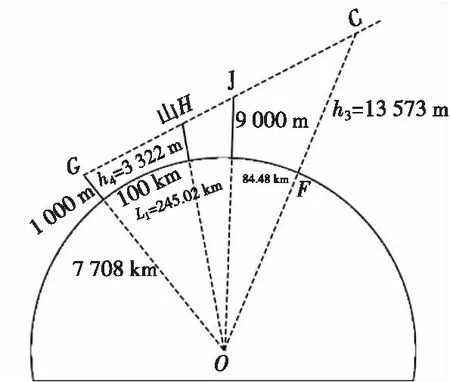
图8 算例第二层遮挡关系图Fig.8 Image of the second layer of occlusion relations of the algorithm
进一步假定存在J点海拔为9 000 m,根据几何换算关系,可反推出J点与G点的地表投影距离为245.02 km,J与C点地表距离为84.48 km,h3=13 573 m。以J点为起点,ae=6 689 km,做第三层等效地球转化前假设距J点50 km的山K(高度h5=11 594 m)是本次转化的“锚点”,则有以下遮挡关系,见图9。
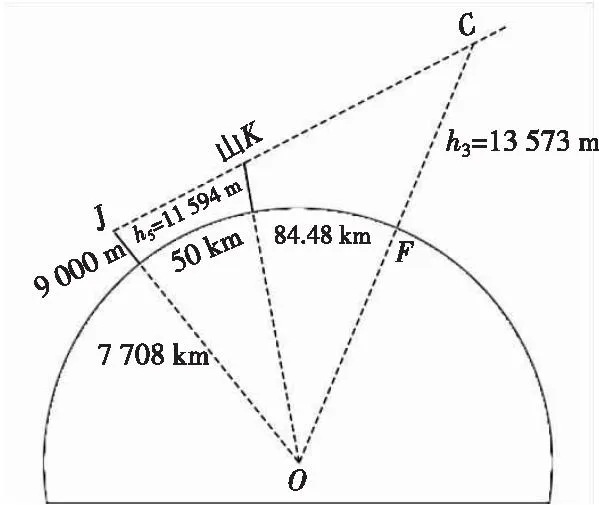
图9 算例第三层等效地球变换前的遮挡关系图Fig.9 Image of occlusion relations in front of the equivalent earth in the third layer of the algorithm
最后以山K遮挡J点为基础,做第三层等效地球转化,见图10,求得h3=13 601 m。
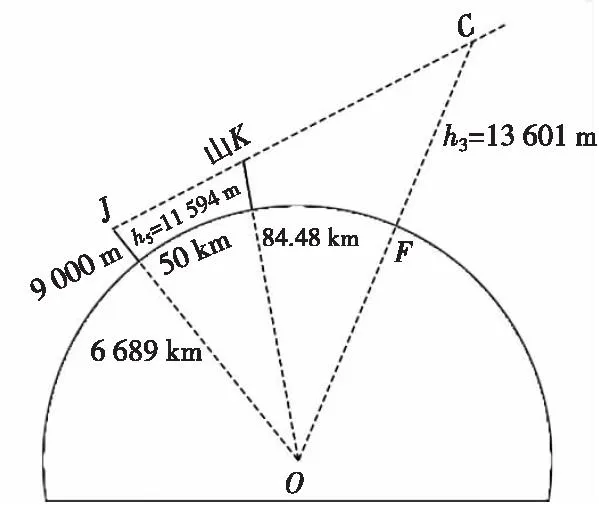
图10 算例第三层等效地球变换后的遮挡关系图Fig.10 Image of occlusion relations after the equivalent earth in the third layer of the algorithm
从修正结果看,h3的取值从13 118 m修正为13 601 m,代表了大气折射的弱化,符合高空域大气折射降低的实际。
2.3 计算结果的分析比较
使用2.2节中的算例,将未做大气折射修正的算法记作f0(l),将使用单层等效地球法修正的算法记作fd1(l),将分层修正的算法记作fd2(l),分别计算地面投影距离lC取[16,400]时各算法计算结果,对比结果见图11。
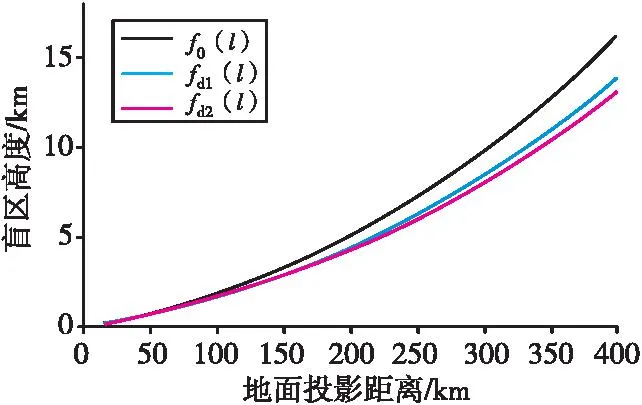
图11 f0(l),fd1(l),fd2(l)随lC变化趋势对比图(h2=222 m)Fig.11 Trends comparative chart,f0(l),fd1(l),fd2(l) with lC(h2=222 m)
为便于分析比对,将算例中的山B高度h2调整为800 m,以增大雷达初始仰角,再次计算f0(l),fd1(l)和fd2(l),对比结果见图12。
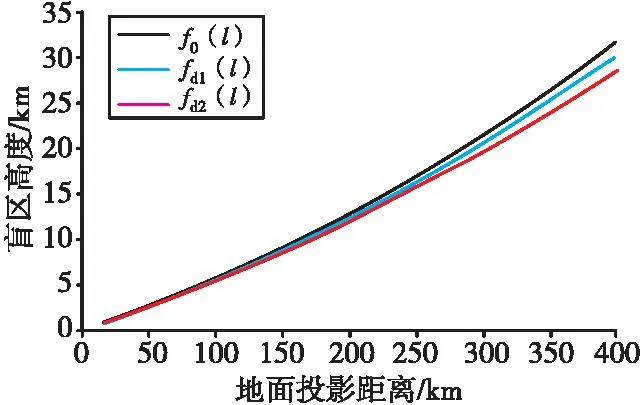
图12 f0(l),fd1(l),fd2(l)随lC变化趋势对比图(h2=800 m)Fig.12 Trends comparative chart,f0(l),fd1(l),fd2(l) with lC(h2=800 m)
设t1(lC)=100%·[f0(lC)-fd1(lC)]/f0(lC),t2(lC)=100%·[f0(lC)-fd2(lC)]/f0(lC),其值可表示两种算法与f0(l)的比例差值。计算h2=222 m和h2=800 m时的t1,t2,结果见图13。
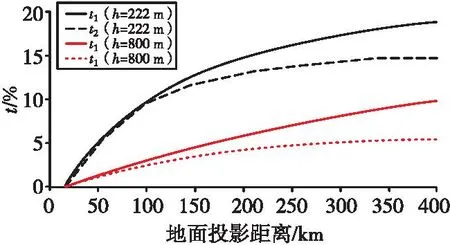
图13 t1,t2随lC变化趋势对比图Fig.13 Trends comparative chart,t1,t2 with lC
分析图11-图13,不难看出:
1) 随着lC距离的增大和电磁波所在空域的提升,fd1(l)和fd2(l)之间无论是绝对差值或是比例差值,均呈现不断扩大趋势。计算结果反映了大气折射现象在高空域减弱这一事实。
2)fd1(l)和fd2(l)的差值与电磁波在高空域的传播距离相关,电磁波越早进入1 km以上空域,两者差值越早开始扩大,但随着电磁波在高空域长时间运行,该差值有逐步趋稳态势。对于防空雷达关注的20 km以下空域,两者的差值比较有限,若对精度要求不高,可以直接使用fd1(l)进行计算。
3) 从t1,t2来看,等效地球法对高仰角的修正效果要明显弱于低仰角的情况,这与Snell定律表述相符,即仰角越高大气折射效应越弱。这也反映了等效地球法对仰角变化具有敏感性。
3 基于二元曲率方程的大气折射修正算法
3.1 求解思路
根据文献[14],大气折射导致雷达波束以曲线形式传播,射线曲率e0定义为曲线上某点切线指向角对弧长的变化率。衡量射线的弯曲程度可用曲率半径ρ=1/e0来表示,曲率半径越大,代表弯曲程度越小,反之越大,其表达式为
(4)
式(4)中,n0为地面大气折射指数,a为地球半径约6 370 km,θ0为射线的初始仰角,n为大气高度h处的大气折射指数,dn/dh为折射指数垂直梯度。由此可见,射线的弯曲是由于存在dn/dh而产生的折射效应,由于n≈1,h≪a,故当dn/dh为恒定值情况下,射线曲率取决于起始角θ0,则曲率半径ρ为恒定值,若将曲线无限延长,射线最终将首尾相接并构成标准圆。若雷达A被山B遮挡,则该曲率圆必过A,B两点,在ρ已知的情况下圆的方程是可求的,继而可修正大气折射。具体解法为:
1) 以地球圆心O为原点,构建平面直角坐标,见图14。假定存在雷达A高度为h1,山B高度为h2,山B遮挡雷达A导致在C点形成高度为h3的雷达盲区,地球半径为a,AB之间地表距离为lB,对应地心角为α,AC对应地表距离为lC,对应地心角为α+β,大气折射形成的曲率圆心为O′,曲率半径为ρ。则有地球方程表达式为x2+y2=a2,A点坐标为(0,a+h1),B点坐标为(asinα,acosα)。h1,h2,lB,lC,a均为已知量,α,β可由已知量推算。
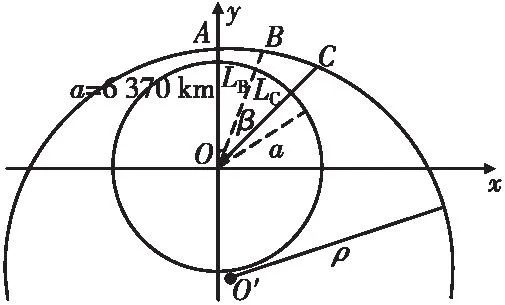
图14 平面直角坐标系构筑图Fig.14 Image of the construction of a planar rectangular coordinate system
2) 求解O′的表达式
首先确定曲率半径ρ。标准大气折射情况下ρS=4a[6],则ρ=ρS/cosθ0。由于ρ≫lB,得θ0≈∠BAO-π/2,△ABO可解,故θ0,ρ可解。
设O′表达式为(x-b)2+(y-c)2=ρ2,将A、B坐标代入,解二元二次方程,排除掉c>0的根项即得到O′的方程表达式。
3) 求解h3
直线OC的表达式为y=x·cot(α+β),将OC表达式与O′的方程表达式联立,再次解二元二次方程,排除掉小于0的根,即可求得C点的坐标,继而求得h3。文中将通过曲率方程法修正大气折射的算法记为fq(l)。
可以看到,曲率方程法具有清晰的物理概念,计算过程简单,能够考虑θ0造成的误差。缺点是解二元二次方程算力代价较大,且dn/dh必须为恒定值,高空大气折射的非线性变化会带来一定误差。
3.2 计算结果的分析比较
仍然使用2.2节中的算例,通过调节h2的取值来实现仰角的变化,评估其对fq(l)和fd(l)计算结果的影响(由于fq(l)无法顾及折射梯度的变化,因此这里选用fd1(l)做计算对比,此处选取标准大气折射下的ae=8 490 km)。设θ0=0的方程算法为fq1(l),实际考虑θ0修正曲率半径的方程算法为fq2(l),lC取[16~400],不同仰角的fd(l),fq1(l)和fq2(l)的计算结果对比见图15和图16。

图15 fd(l),fq1(l),fq2(l)取值计算图(h2=2 000 m,θ=7.188°,ρ=25 681.84 km)Fig.15 Value calculation chart of fd(l),fq1(l),fq2(l)(h2=2 000 m,θ=7.188°,ρ=25 681.84 km)
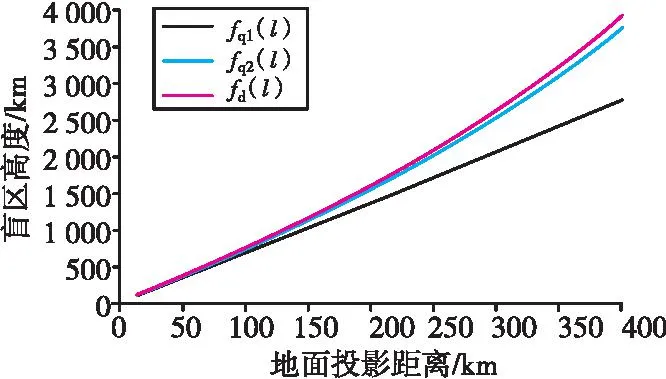
图16 fd(l),fq1(l),fq2(l)取值计算图(h2=100 000 m,θ=81.25°,ρ=167 495 km)Fig.16 Value calculation chart of fd(l),fq1(l),fq2(l)(h2=100 000 m,θ=81.25°,ρ=167 495 km)
由图15可知,由于cosθ在近零区间变化的钝性,导致ρ的变化非常不明显。因此,fd(l),fq1(l)和fq2(l)的计算结果差异很小。
当θ0增大到一定程度后,fq1(l)与fq2(l)的计算差值逐渐明显,而fd(l)的变化趋势总体与fq2(l)相同,如图16所示。
通过图15和图16不难得出,在起始仰角如此大幅变化的情况下,fq(l),fd(l)的计算结果呈现出高度拟合性,这至少能够说明两点:
1) 由于fq(l)和fd(l)采用了完全不同求解思路,而最终计算结果的拟合性证实了两种方法均为可信算法。
2) 由于fq(l)顾及了起始仰角对计算结果的影响,fq(l)与fd(l)的高度重合结合2.3节中fd(l)的敏感性结论,表明了θ0≈0并不是等效地球算法的限制条件。
4 结论
本文首次系统研究了雷达地形遮蔽盲区计算中大气折射的修正方法,并针对大气折射梯度非线性变化带来的误差,提出了借用“锚点”的概念实现分层等效地球的方法;同时,针对起始仰角θ0可能带来的误差,提出了构建曲率方程的方法评估仰角变化对计算结果的影响。最后从多维度检验和验证实现了大气折射修正的等效地球半径法和曲率方程法的互洽,结果表明:
1) 对于5 km以下的中低空大气,单层等效地球半径法和二元曲率方程法精确度基本能够满足防空雷达地形遮蔽盲区计算的需求;当空域提升至5 km以上时,若对计算精度有较高要求,则需选用多层等效地球半径法进行修正。
2) 经与二元曲率方程法对比检验,证明等效地球半径法考虑了起始仰角对计算结果造成的扰动,可适用于起始角θ0≠π/2的计算条件。
3) 若以算力代价来看,等效地球半径法不涉及高次元计算,计算速度较快。若以建模便捷性来看,二元曲率方程法物理概念明晰,不涉及对地球的变换,更适合GIS技术背景下的模型构造和可视化呈现。

