重力场作用下的引信球转子动力学特性数值模拟

刘艳欣,闻 泉,王雨时,朱乐乐,张 斌

(1.南京理工大学机械工程学院,江苏 南京 210094;2.上海航天电子技术研究所,上海 201108)

0 引言

随着引信技术的不断发展,引信可用空间小与其高可靠性、高安全性的矛盾日益突出。旋转弹引信的安全性和可靠性主要受解除隔离距离短、散布大和可用空间较小的影响。引信球转子机构具有隔爆功能,同时具有延迟解除隔离距离长、体积较小、成本较低、结构简单和易于加工的显著优势。因此,深入研究球转子理论,并将其不断发展和完善具有重要意义。

诸多学者对球转子的研究主要聚焦于球转子的数理模型。文献[1-2]建立了球转子质心与形心重合,且偏离弹丸轴线的运动微分方程,并分析得出了求解微分方程的初始条件和球转子起动的判定公式。在此基础上,文献[3-6]结合欧拉动力学,建立了球转子质心与形心不重合,且偏离弹丸轴线的运动微分方程,并系统分析了球转子起动特性、解除保险特性和运动终止时刻的特性。通过欧拉动力学建立的球转子运动微分方程存在奇异解,文献[7]利用四元数建立了线性的球转子运动微分方程组。文献[8]建立了考虑弹丸章动和进动条件下引信球转子运动微分方程组。文献[9]分析得出了考虑弹丸章动和进动条件下球转子起动时刻的初始条件,并利用ADAMS软件研究了弹丸章动和进动对球转子解除保险特性的影响。上述文献在研究球转子理论时,因球转子质量较小,常常被作为小量忽略。但随着引信球转子在工程实践中的广泛应用,专家将低速旋转弹引信中出现的可靠性问题与球转子重力关联起来。文献[10-11]研究表明,在低转速条件下重力对球转子解除保险特性影响较大。文献[9]通过ADMAS软件仿真研究表明,弹丸在低速条件下考虑重力时的球转子转正时间相对于不考虑重力时缩短了约12%。由此可见,球转子在低速条件下,重力是不可忽略的。

本文应用刚体动力学、欧拉动力学以及外弹道学理论,通过分析引信球转子的力学环境,建立在重力场作用下的引信球转子动力学模型,并采用Matlab软件编制数值模拟程序;以典型引信球转子为例,通过吉尔算法进行数值模拟,研究低速旋转弹引信球转子机构的动力学特性。

1 重力场作用下的球转子动力学模型

1.1 基本假设与运动坐标系

在建立重力场作用下的球转子动力学模型时,除了沿用文献[1,6]的基本假设外,还假设球转子在解除保险前,弹丸在弹道直线上运动,因此弹丸弹道倾角δ=δ0(δ0为弹丸发射角)。球转子运动坐标系如图1所示。关于球转子坐标系建立的详细过程可参见文献[12]。

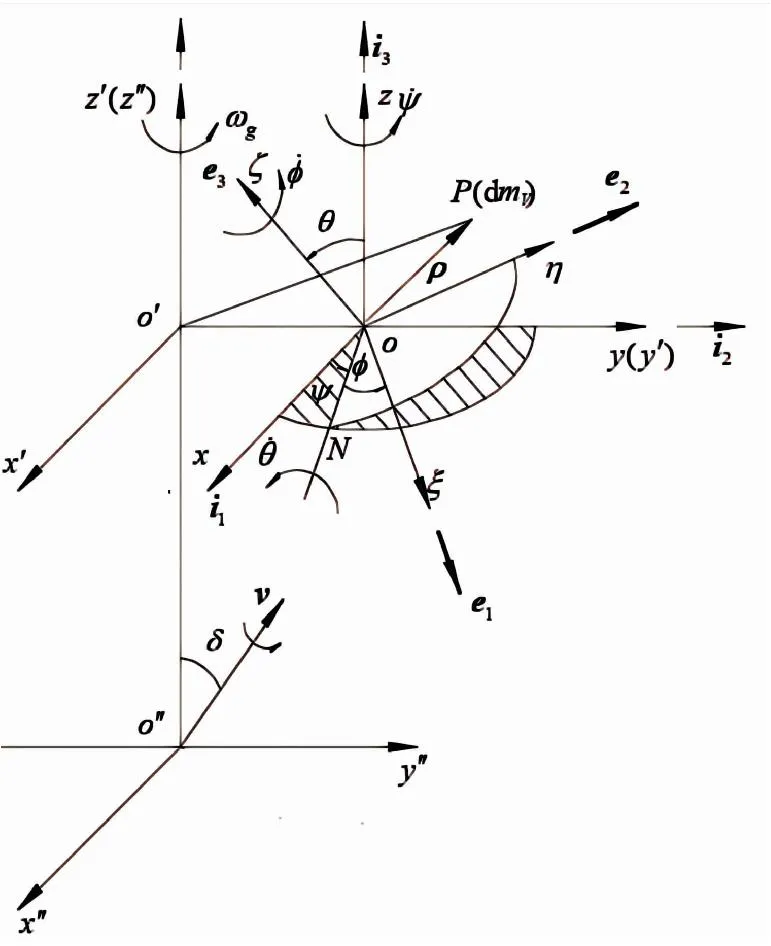
图1 球转子运动坐标系[12]Fig.1 Coordinate system of ball rotor

1.2 球转子动力学分析

所研究的引信球转子所受外力及其外力矩为:球转子重力主矢G,球转子重力主矩MG;球转子腔室对球转子的约束反力Fr,转子所受摩擦力主矩Mf;后坐力主矢Fs或爬行力主矢Fp,后坐力主矩Ms或爬行力主矩Mp;弹丸自转产生的离心惯性力主矢Fc,弹丸自转产生的离心惯性力主矩Mc;哥氏惯性力主矢Fk,哥氏惯性力主矩Mk。

本节将详细论述球转子重力主矢G及其主矩MG和球转子腔室对球转子约束反力Fr的推导过程。其他主矢和主矩的详细推导过程可参见文献[6,12],本文不再详细赘述。

1.2.1重力主矢G

球转子重力在定坐标系Oxyz中的表达式为

G=Gxi1+Gyi2+Gzi3=
-Gsin(90°-δ)cos(ωgt)i1+Gsin(90°-δ)sin(ωgt)i2-
Gcos(90°-δ)i3=
-Gcosδcos(ωgt)i1+Gcosδsin(ωgt)i2-Gsinδi3,

(1)

式(1)中,δ为弹丸弹道倾角,t为球转子转正时间(从弹丸飞离炮口开始计时),ωg为弹丸炮口转速。

球转子重力表达式为

G=mg,

(2)

式(2)中,m为球转子质量,g为当地重力加速度。

1.2.2重力主矩MG

在动参考系中,假设球转子单位质量dmV内任意一点P的矢径为OP=ρ,dmV所受重力主矩dMG=ρdG,可得球转子所受重力主矩为

(3)

式(3)中,ρ=ξe1+ηe2+ζe3。

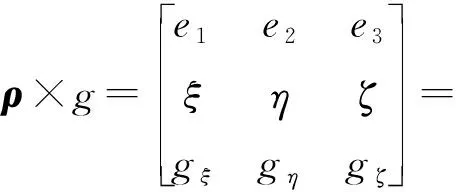
(4)

式(4)中,gξ,gη和gζ可由式(5)求得。

由文献[12]给出的球转子动坐标系与定坐标系Oxyz之间变换所需方向余弦矩阵A,可得球转子重力加速度在动坐标系Oξηζ中的表达式为

(5)

将式(4)和式(5)代入式(3)可得

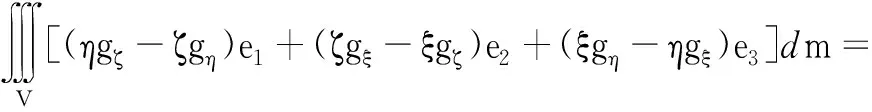
(6)

式(6)中,ξM,ηM和ζM分别为球转子质心M在动坐标系Oξ轴、Oη轴和Oζ轴上的坐标。

球转子重力主矩MG在动系参考系Oξ轴、Oη轴和Oζ轴上的投影分别为

MGξ=mg{ηM[-a31cosδcos(ωgt)+a32cosδsin(ωgt)-a33sinδ]-
ζM[-a21cosδcos(ωgt)+a22cosδsin(ωgt)-a23sinδ]},

(7)

MGη=mg{ζM[-a11cosδcos(ωgt)+a21cosδsin(ωgt)-a31sinδ]-
ξM[-a31cosδcos(ωgt)+a32cosδsin(ωgt)-a33sinδ]},

(8)

MGζ=mg{ξM[-a21cosδcos(ωgt)+a22cosδsin(ωgt)-a23sinδ]-
ηM[-a11cosδcos(ωgt)+a21cosδsin(ωgt)-a31sinδ]}。

(9)

1.2.3球转子腔室对球转子的约束反力Fr

球转子与其腔室摩擦的受力分析示意图可参考文献[6]。在点M处,球转子腔室对球转子的摩擦力大小为

FrM=(Fsz+Fkz+Gz)f1,

(10)

或

FrM=(Fpz+Fkz+Gz)f3,

(11)

式中,f1和f3分别为球转子与其上、下腔室间的库伦摩擦系数;Fsz和Fpz分别为后坐力和爬行力在定坐标系Oz轴上的投影,Fkz为哥氏惯性力在定坐标系Oz轴上的投影,可参见文献[6];Gz为球转子重力在定坐标系Oz轴上的投影,由式(1)求得。

在点S处,球转子腔室对球转子的摩擦力为

(12)

式(12)中,E1×3为1×3阶矩阵,各元素均为1;f2为球转子与其腔室侧面的库伦摩擦系数;Gx和Gy分别为重力在定坐标系Ox轴和Oy轴上的投影,可由式(1)求得。Fcx和Fkx分别为离心惯性力和哥氏惯性力在定坐标系Ox轴上的投影,Fcy和Fky是离心惯性力和哥氏惯性力在定坐标系Oy轴上的投影。Fcx,Fkx,Fcy和Fky的表达式可参见文献[6]。联立式(10)-式(12),并结合文献[6]中球转子在点M,S所受摩擦力矩MfM和MfS的表达式,可得MfM和MfS分别在动坐标系Oξ轴、Oη轴和Oζ轴上的投影MfMξ,MfMη,MfMζ和MfSξ,MfSη,MfSζ。

1.3 重力场作用下的球转子运动微分方程组

球转子所受摩擦力矩Mξ,Mη和Mζ分别在动坐标系Oξ轴、Oη轴和Oζ轴上的投影为

(13)

式(13)中,E6×1为6×1阶矩阵,各元素均为1。Msζ,Mcζ,Mkζ,Msη,Mcη,Mkη和Msζ,Mcζ和Mkζ为后坐力主矩Ms、弹丸自转产生的离心惯性力主矩Mc和哥氏惯性力主矩Mk分别在Oξ轴、Oη轴和Oζ轴上的投影,可参见文献[6]。

根据欧拉动力学方程,可得考虑重力情况下球转子运动微分方程组为

(14)

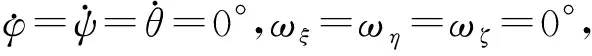
2 重力场作用下的球转子动力学特性数值模拟

为了研究球转子因武器平台转速不同而导致的重力对球转子机构解除保险特性影响程度的差异性,选取了较为典型的低速、中速、高速三种不同转速的旋转弹引信球转子为算例,应用Matlab软件编制数值模拟程序,采用吉尔算法进行数值模拟,并从解除保险距离和动态平衡角两方面进行对比分析。

2.1 球转子数值模拟所用参数

所选取的低速旋转弹为84 mm口径炮弹,其膛口转速为449 rad/s;选取的中速旋转弹为40 mm口径榴弹,其膛口转速为1 256 rad/s;选取的高速旋转弹为57 mm 口径榴弹,其转速为3 145 rad/s。三种不同转速的旋转弹所配引信球转子基本上涵盖了常规旋转弹引信球转子的特点,数值模拟所用相关参数,如表1-表3所列。

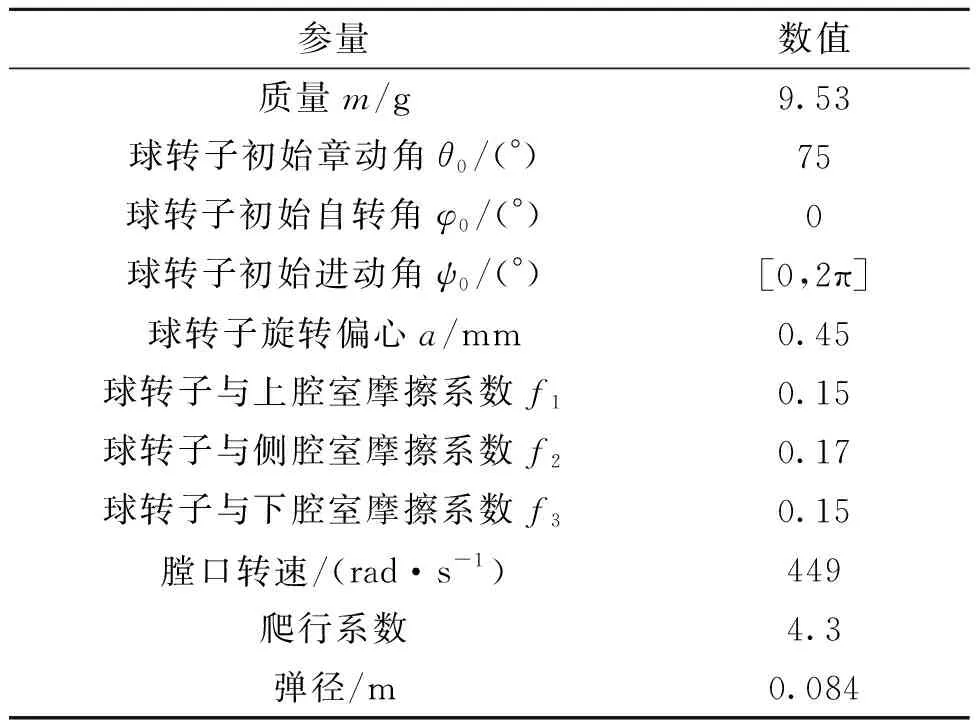
表1 低速旋转弹引信球转子数值模拟所用参数Tab.1 Parameters used for numerical simulation ofa low-speed rotary projectile fuze ball rotor

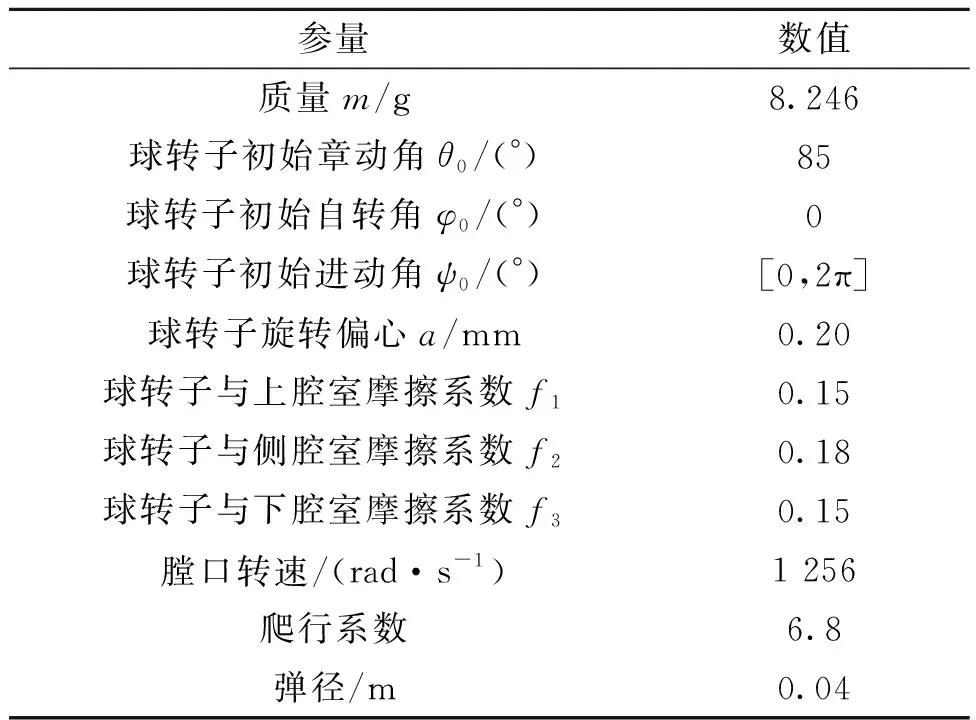
表2 中速旋转弹引信球转子数值模拟所用参数Tab. 2 Parameters used in numerical simulation ofa medium-speed rotary projectile fuze ball rotor

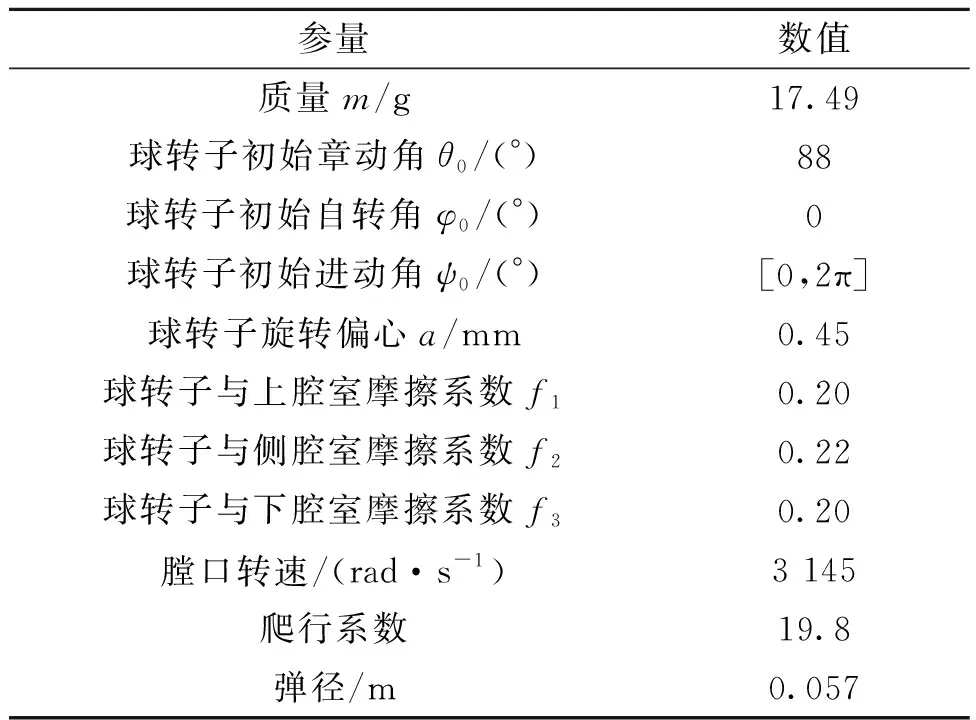
表3 高速旋转弹引信球转子数值模拟所用参数Tab.3 Parameters used in numerical simulation ofa high-speed rotary projectile fuze ball rotor

2.2 数值模拟结果

表4-表6列出了球转子初始进动角在0°～180°范围内变化,有无重力时低、中、高三种不同转速的引信球转子解除隔离距离数值模拟结果。表7-表9列出了球转子初始进动角在0°～180°范围内变化,有无重力时低、中、高三种不同转速的引信球转子动态平衡角数值模拟结果。图2-图4给出了球转子初始进动角在0°～180°范围内变化时,重力场对低、中、高三种不同转速的引信球转子动力学特性的影响。表中“-”表示球转子未解除保险。

表4 低速旋转弹引信球转子有无重力时解除隔离距离数值模拟结果Tab.4 Numerical simulation results of release safety distance with or without gravity of the fuze ball rotor for a low-speed rotary projectiles

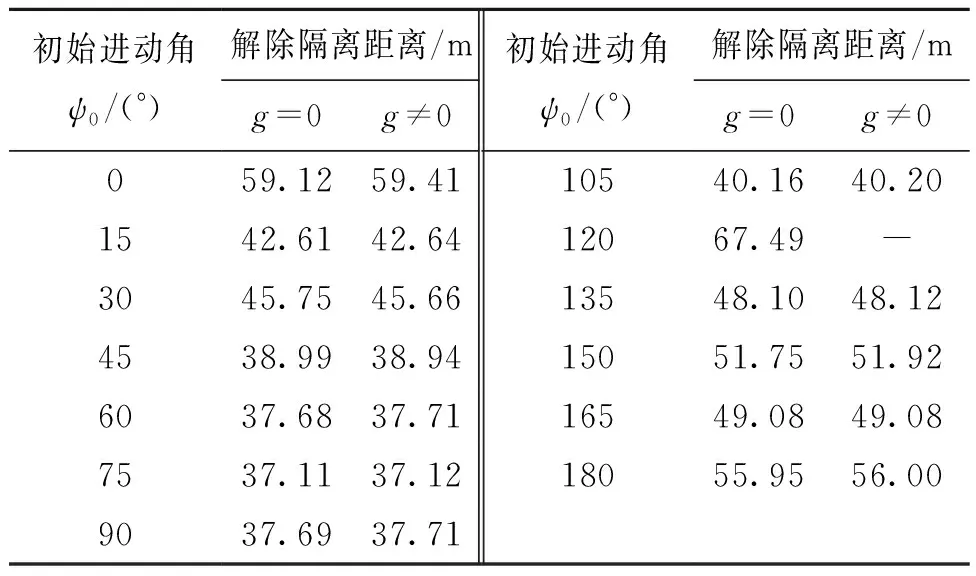
表6 高速旋转弹引信球转子有无重力时解除隔离距离数值模拟结果Tab. 6 Numerical simulation results of release safety distance with or without gravity of the fuze ball rotors for a high-speed rotary projectiles

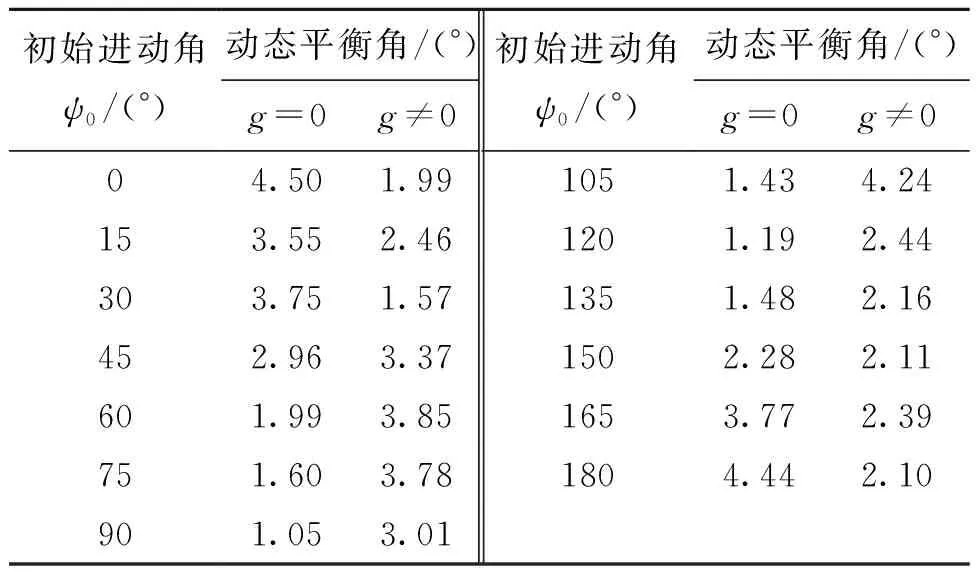
表7 低速旋转弹引信球转子有无重力时动态平衡角数值模拟结果Tab.7 Numerical simulation results of dynamic equilibrium angle with or without gravity of the fuze ball rotor for a low-speed rotary projectiles

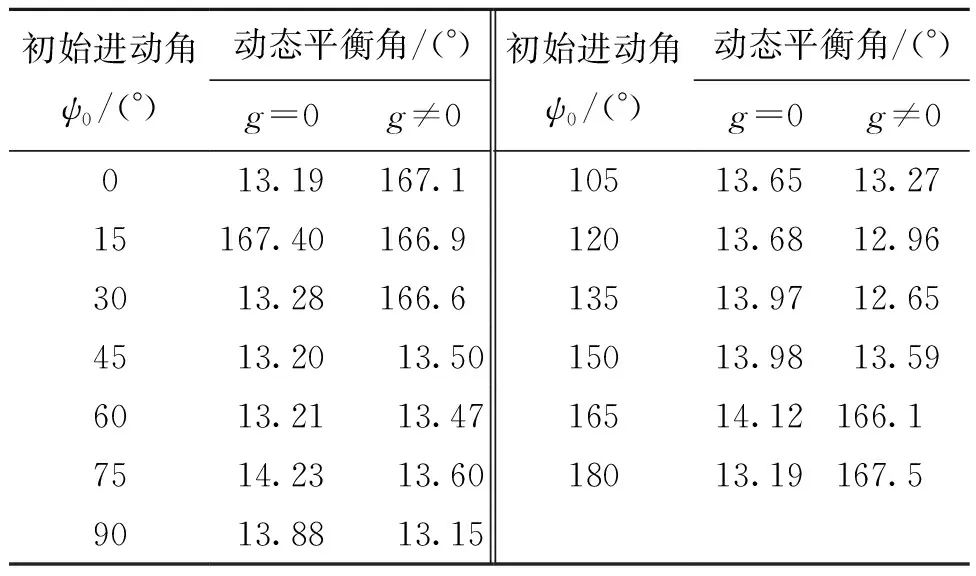
表8 中速旋转弹引信球转子有无重力时动态平衡角数值模拟结果Tab. 8 Numerical simulation results of dynamic equilibrium angle with or without gravity of the fuze ball rotor for a medium-speed rotary projectiles

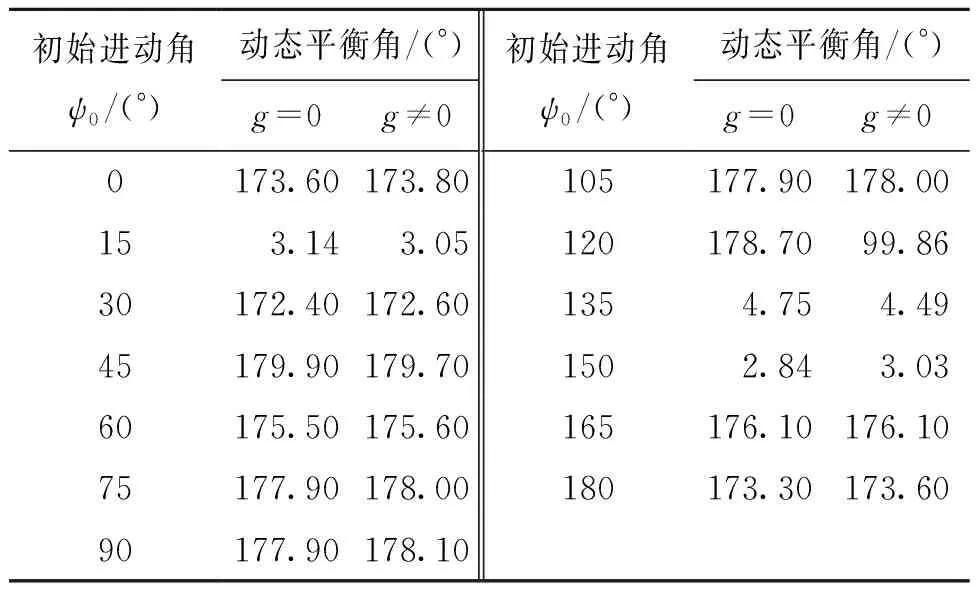
表9 高速旋转弹引信球转子有无重力时动态平衡角数值模拟结果Tab.9 Numerical simulation results of dynamic equilibrium angle with or without gravity of the fuze ball rotors for a high-speed rotary projectiles

图2 重力场对低速旋转弹引信球转子动力学特性的影响Fig.2 Influence of gravity field on rotordynamic characteristics of fuze ball rotor for low-speed rotary projectiles

2.3 结果分析与讨论

为了研究在重力场作用下引信球转子的动力学特性,基于数理统计法,将低、中、高三种不同转速的旋转弹引信球转子数值模拟结果进行处理,得到了初始进动角在0°～180°范围内变化时的解除隔离距离和动态平衡角的数据特征值,如表10所列。

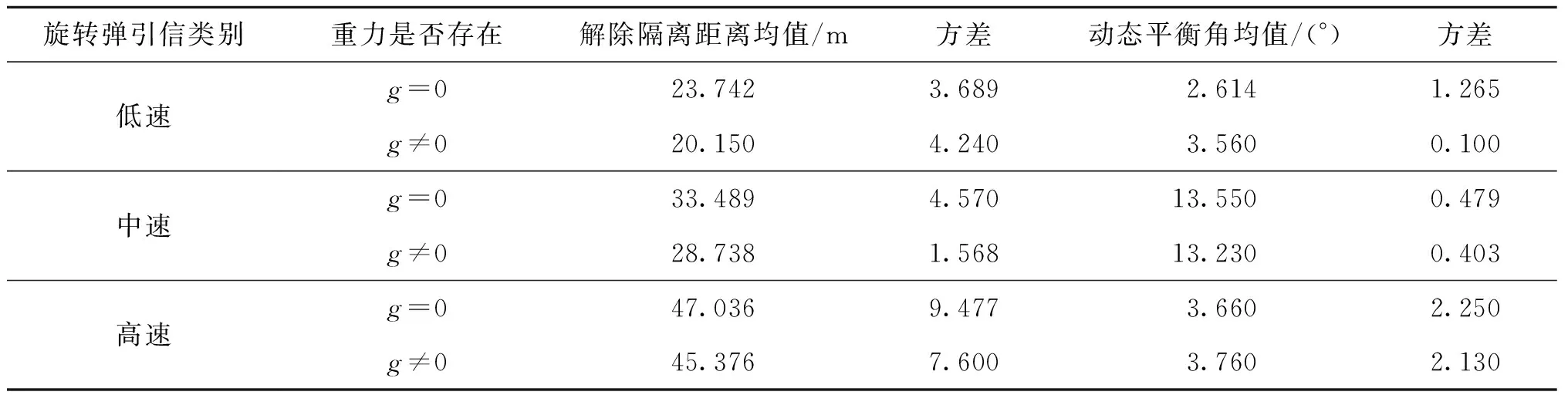
表10 有无重力时低、中、高三种不同转速的球转子解除隔离距离与动态平衡角数据特征值Tab.10 Characteristic values of the release fuze distance and dynamic balance angle data of ball rotors with and without gravityr under low-speed、medium-speed and high-speed rotary projectile

从球转子解除隔离距离、动态平衡角和解除隔离可靠性三方面对表10结果进行分析。

无重力条件下低速旋转弹引信球转子的解除隔离距离均值为23.74 m,在重力场作用下的低速旋转弹引信球转子的解除隔离距离均值为20.15 m。由此可知,重力将低速旋转弹引信球转子的解除隔离距离缩短了15.76%,同时增大了散布。无重力条件下中速旋转弹引信球转子的解除隔离距离均值为33.489 m,在重力场作用下的中速旋转弹引信球转子的解除隔离距离均值为28.738 m。由此可知,重力将中速旋转弹引信球转子的解除隔离距离缩短了14.19%,同时减小了散布。无重力条件下高速旋转弹引信球转子的解除隔离距离均值为47.036 m,在重力场作用下的高速旋转弹引信球转子的解除隔离距离均值为45.376 m。由此可知,重力将高速旋转弹引信球转子的解除隔离距离缩短了3.53%,同时减小了散布。

综上所述,在重力场作用下的低速旋转弹引信球转子解除隔离距离至少缩短14.00%。因此,低速旋转弹引信球转子的重力效应对引信解除隔离距离影响较大。

无重力条件下低速旋转弹引信球转子的动态平衡角方差为1.265,在重力场作用下的低速旋转弹引信球转子的动态平衡角方差为0.100。由此可知,重力增大了低速旋转弹引信球转子的动态平衡角,同时减小了散布。无重力条件下中速旋转弹引信球转子的动态平衡角方差为0.479,在重力场作用下的中速旋转弹引信球转子的动态平衡角方差为0.403。由此可知,重力减小了中速旋转弹引信球转子的动态平衡角,同时减小了散布。无重力条件下高速旋转弹引信球转子的动态平衡角方差为2.250,在重力场作用下的高速旋转弹引信球转子的动态平衡角方差为2.13。由此可知,重力增大了高速旋转弹引信球转子动态平衡角,同时减小了散布。

综上所述,在重力场作用下的低速旋转弹引信球转子的动态平衡角散布至少减小18.6 %。

由图3可知,中速旋转弹引信球转子在进动角为0°～30°和165°～180°时的动态平衡角均大于90°,所以,中速旋转弹引信球转子的重力效应可以使其发生反转。由图4可知,高速旋转弹引信球转子的进动角除了135°外,其他情况下的动态平衡角均大于90°,所以,高速旋转弹引信球转子的重力效应可以使其发生反转。

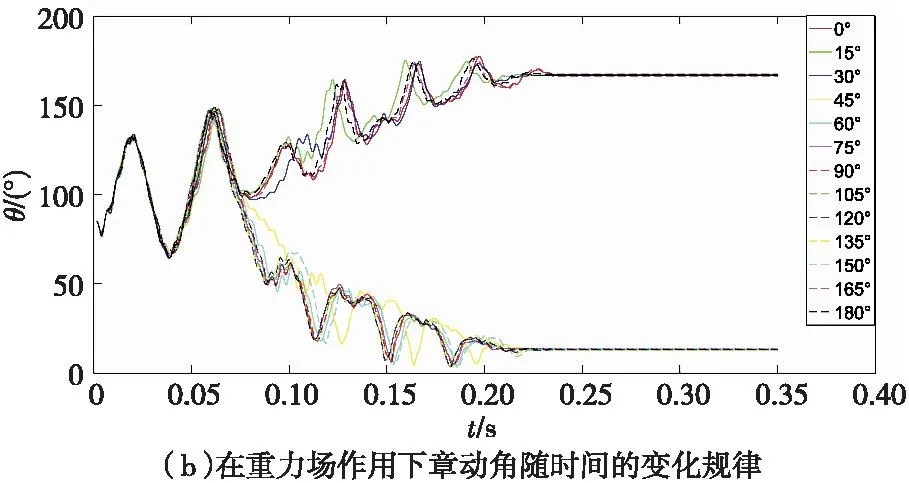
图3 重力场对中速旋转弹引信球转子动力学特性的影响Fig.3 Influence of gravity field on rotordynamic characteristics of medium-speed rotary fuze ball rotor

图4 重力场对高速旋转弹引信球转子动力学特性的影响Fig.4 Influence of gravity field on rotordynamic characteristics of high-speed rotary projectile fuze ball rotor

综上所述,低速旋转弹引信球转子的重力效应可以提高引信发火可靠性,同时也可使球转子发生反转,但对解除隔离可靠性的影响较小。

3 数值模型置信度评估

为了评估在重力作用下的引信球转子动力学模型的置信度,表11列出了文献[9]基于ADAMS仿真平台所得引信球转子解除隔离距离受重力效应的影响程度和本文数值模拟所得结果。

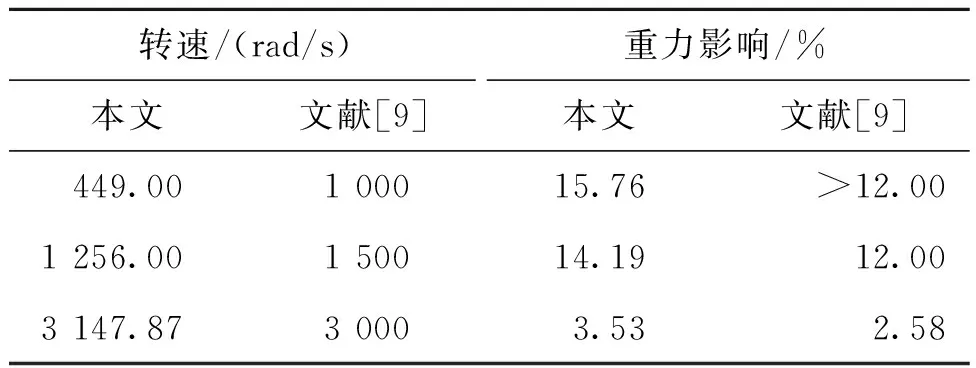
表11 ADAMS仿真平台所得球转子解除隔离距离受重力效应的影响程度与本文数值模拟结果对比Tab.11 The degree of influence of gravity effect of the ball rotor release distance obtained by the ADAMS simulation platform is compared with the numerical simulation results in this paper

综上所述,本文在Matlab软件场景下的数值模拟结果与文献[9]基于ADAMS仿真平台所得引信球转子解除保险距离受重力效应的影响程度较为接近。因此,本文数值模拟结果具有较高的置信度。

4 结论

本文应用刚体动力学、欧拉动力学以及外弹道学理论,通过分析引信球转子的力学环境,建立在重力场作用下的引信球转子动力学模型,并应用Matlab软件编制数值模拟程序;以典型引信球转子为例,通过吉尔算法进行数值模拟,研究低速旋转弹引信球转子机构的动力学特性。数值模拟结果表明:在重力场作用下的低速旋转弹引信球转子的解除保险距离至少缩短14.00%,动态平衡角散布至少减小18.60%。低速旋转弹引信球转子的重力效应可以提高引信发火可靠性,同时也可使球转子发生反转,但对解除保险可靠性的影响较小。