基于协方差矩阵Toeplitz重构的MUSIC算法的波达方位估计方法

王绪虎，侯玉君，金序，田雨，王辛杰，李恩玉

(青岛理工大学信息与控制工程学院，山东青岛 266520)

0 引言

波达方向(Direction of Arrival,DOA)估计是阵列信号处理的一个重要研究方向[1]。由于水声信道的复杂性，信号在实际环境传播中存在多径传播和同频干扰，入射到阵列的信号多为相干信号[2]，传统的DOA 估计方法性能将会下降，甚至完全失效[3-4]。因此，相干信号的方位估计成为重要的研究方向之一[5]。

解相干方法通常分为两类，一类是降维处理[6]，如空间平滑方法，这类方法能够很好地解相干，但是损失了部分阵列的有效孔径[7]。另一类是非降维处理，如最大似然估计方法[8]，这类方法对相干信号有效，但通常利用多维搜索进行计算，计算量巨大，且求解过程中存在局部最优解的问题，实用性不强。文献[9]提出了一种基于前向和后向部分托普利兹(Toeplitz)矩阵重构的改进方位估计方法，利用样本协方差矩阵的半行来重构数据矩阵，解决了因入射信号与角度间存在相位差造成DOA估计性能降低的问题。文献[10]提出了一种基于多重Toeplitz矩阵集重构的相干信号估计方法，该方法利用阵元接收数据构造托Toeplitz矩阵，通过厄尔米特(Hermitian)转置矩阵修正和正反向平滑运算得到满秩矩阵实现解相干，具有较好的估计精度和成功分辨率。文献[11]提出了一种双目标相干源窄带信号波达方向估计方法，该方法不受信号相关性的影响，所需数据量少，提高估计精度的同时降低了计算量。文献[12]针对基于子空间方法不能解决信号数量大于传感器数量及基于稀疏性方法总是受到基失配影响的问题，提出了一种协方差矩阵重构方法，提高了DOA估计的速度和精度。文献[13]提出了一种基于均匀线阵改进的多重信号分类(Modify Multiple Signal Classification,MMUSIC)算法，在不增加计算量的前提下有效降低了信号间的相干系数，提升了MUSIC 算法的估计性能，但是该方法仅适用于线列阵。文献[14]提出了一种基于重构噪声子空间(Reconstructed Noise Subspace,RNS)的相干信号估计方法，并且在低信噪比、少快拍下估计精度优于MMUSIC 方法，但是当信号入射间隔较小或者存在多个相干信源时，DOA 估计性能会严重降低。

因此，本文首先根据样本协方差矩阵及其翻转矩阵构造新协方差矩阵，并利用新协方差矩阵构造Toeplitz 矩阵，然后利用MUSIC 算法进行方位估计。仿真实验和湖上实验数据处理结果表明，与MMUSIC 方法和基于RNS 的估计方法相比，本文所提方法提高了DOA估计精度和方位分辨能力。

1 信号模型

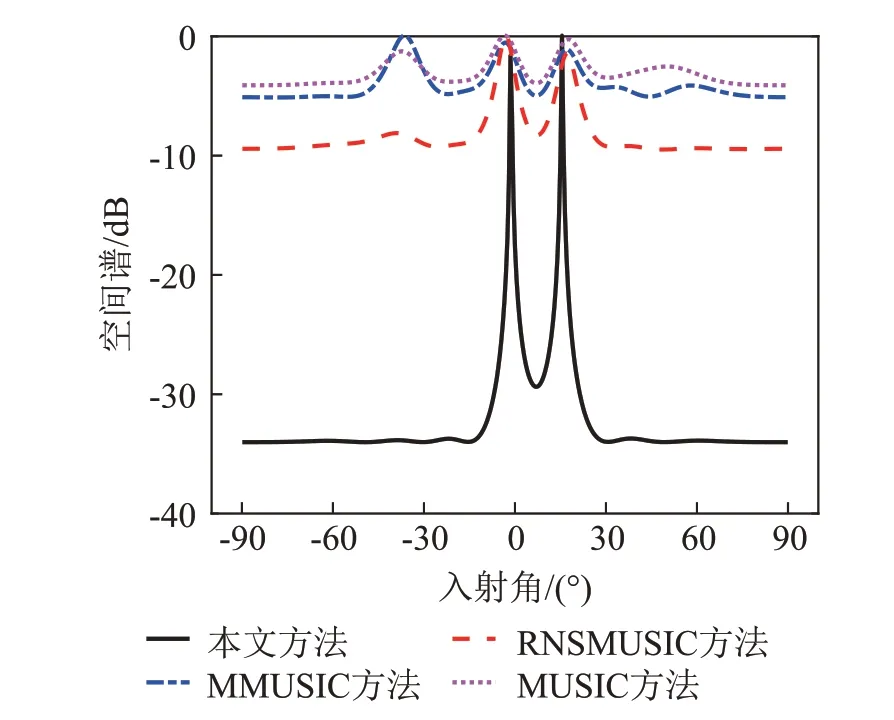
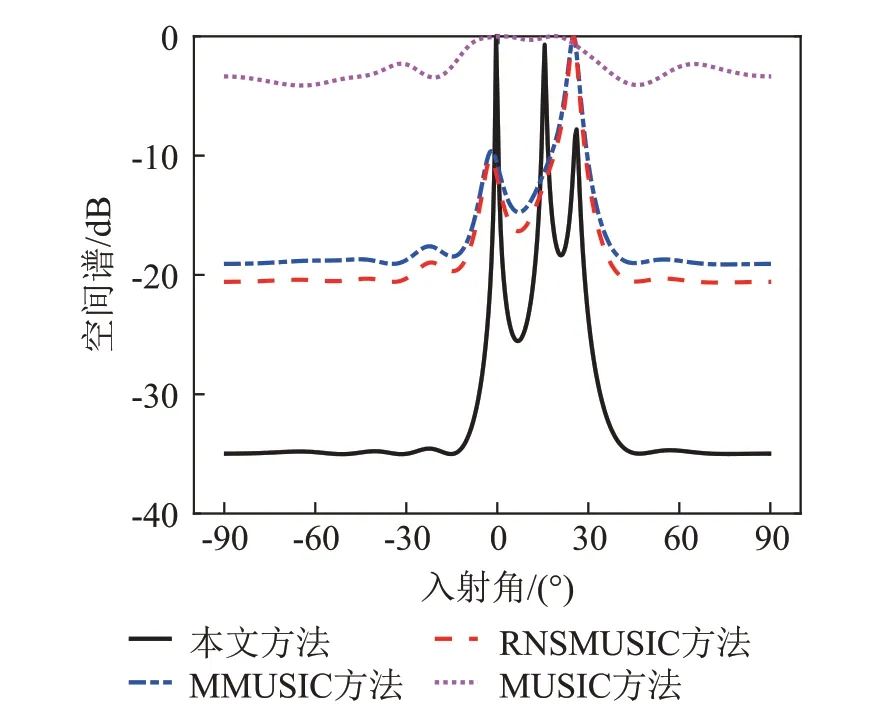
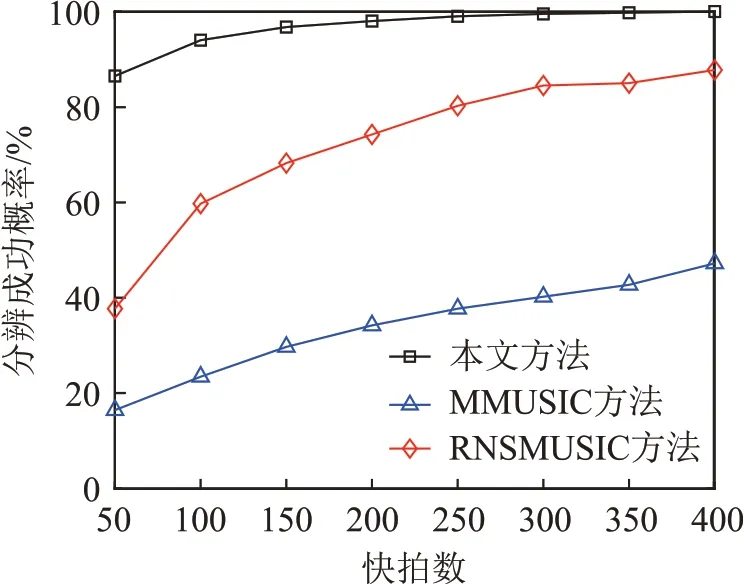
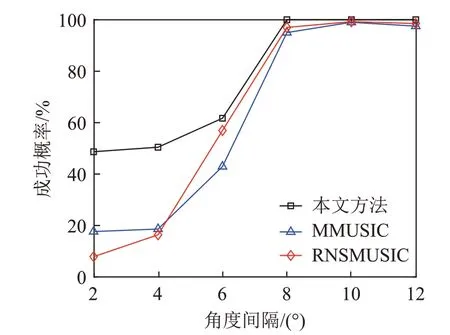
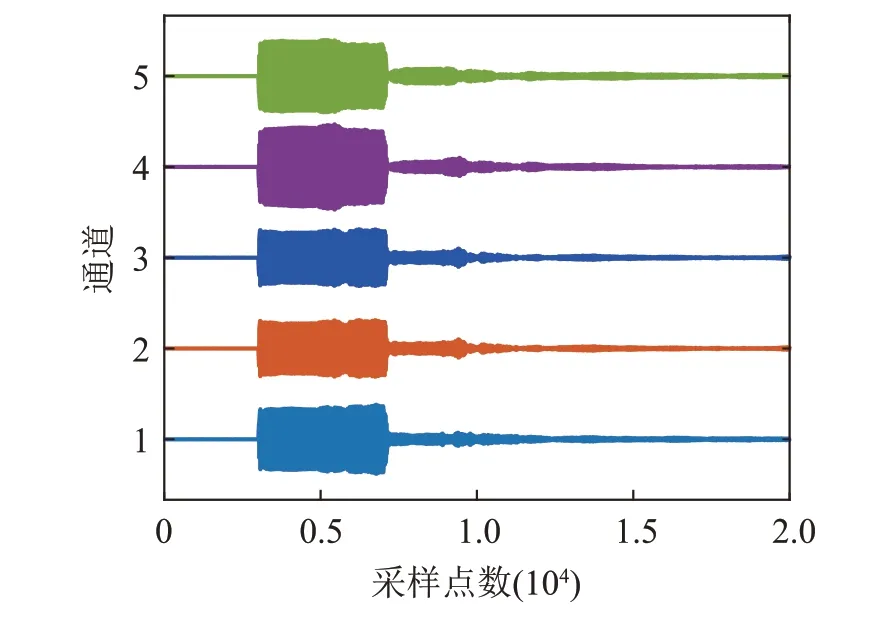
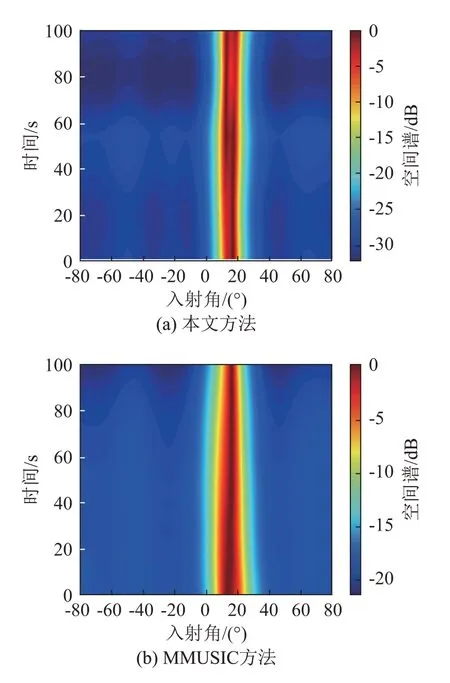
假设有K个远场窄带信号入射到由M个阵元构成的均匀线列阵上(K

图1 均匀线阵模型Fig.1 Uniform linear array model

以左侧第一个阵元为参考，则此时的阵列导向矢量为

第m个阵元接收到的信号可以表示为

其中：m=1,2,…,M，sk(t)(k=1,2,…,K)是第k个入射到均匀线列阵上的信源；λ是信号波长，nm(t)是高斯白噪声，θk是第k个信源的入射角度，[ ∙]T表示矩阵的转置。

此时的阵列数据接收矩阵形式可以表示为

其中：

由式(3)中的X(t)，可得阵列输出信号的协方差矩阵为

其中：RS=E[S(t)SH(t)]表示信号的协方差矩阵，σ2表示噪声方差，IM表示M阶单位矩阵，[ ∙]H表示矩阵的共轭转置。

2 算法原理

2.1 MUSIC算法

对式(8)中的协方差矩阵RX进行特征值分解可得：

其中：US表示由K个大特征值对应的特征向量组成的信号子空间，ΣS表示大特征值对应的对角矩阵，UN表示由M-K个小特征值对应的特征向量组成的噪声子空间，ΣN表示小特征值对应的对角矩阵。因为阵列流型矩阵A(θ)中的每一个列向量都与噪声子空间正交，所以理想状态下有：

对式(11)的空间谱进行谱峰搜索得到DOA的估计值。当入射信号不相干时，该方法具有较好的方位估计性能，当入射信号相干时，该方法性能严重降低，不能正确地估计出入射信号的方位。

2.2 MMUSIC算法

由于MUSIC 算法无法对相干信号进行方位估计，研究者在该方法基础上提出了一种能够估计相干信号的改进MUSIC 算法[13]。改进算法对阵列数据接收矩阵X(t)预处理，得到一个新的数据接收矩阵Y(t)，表达式为

其中：J是M×M阶副对角线元素为1、其余元素均为0的反对角矩阵；X*(t)为阵列接收数据矩阵X(t)共轭矩阵；[ ∙]*表示矩阵的共轭。

此时，信号的协方差矩阵可表示为

对协方差矩阵RX、RY取平均得到新的协方差矩阵：

然后对新协方差矩阵R进行特征分解，得到新信号子空间和新噪声子空间，将新噪声子空间代入式(11)计算空间谱，然后对空间谱进行谱峰搜索，谱峰对应的角度即为入射信号方位的估计值。该方法可以有效地估计出两个相干信号的入射方位。

2.3 RNSMUSIC算法

MMUSIC算法只利用了X(t)和Y(t)的自协方差信息，重构噪声子空间MUSIC(Reconstructed Noise Subspace Multiple Signal Classification,RNSMUSIC)算法[14]不仅利用了X(t)和Y(t)自相关信息，还利用了两者之间的互协方差信息。

利用X(t)和Y(t)的自协方差矩阵、互协方差矩阵构造增广矩阵RA，计算方法为

其中：RXY=E[X(t)YH(t)]是X(t)和Y(t)的互协方差矩阵，RYX=E[Y(t)XH(t)]是Y(t)和X(t)的互协方差矩阵。

对RA做奇异值分解，得到特征值矩阵Z和特征向量矩阵U：

对式(14)中的新协方差矩阵R做奇异值分解，得到特征值矩阵Z1和特征向量矩阵U1：

将特征值矩阵Z和Z1的对角线元素按顺序比较，选取较大值构成新的特征值矩阵Z0：

其中：λ1≥λ2≥…≥λM。

根据特征值矩阵Z0重构新的特征向量矩阵U0：

从矩阵U0中选择第个K+1列到第M列构成新的噪声子空间Un：

然后根据Un构造空间谱函数：

最后，通过谱峰搜索确定DOA的估计值。

虽然MMUSIC 算法和RNSMUSIC 算法都能够准确地估计两个相干信号的波达方向，但是相干信号的个数超过两个时，这两种方法的方位估计性能下降。

2.4 本文方法

由于噪声的影响，破坏了协方差矩阵的Hermi‐tian 特性，导致方位估计性能下降，针对该问题，本文通过对接收数据协方差矩阵进行Toeplitz重构来改善方位估计性能。本文方法选取接收数据协方差矩阵的第一行和第一列，构造具有Hermitian 特性的新协方差矩阵，然后利用MUSIC 方法估计目标方位。该方法可以估计出相干信号，并且不降低空间分辨力[15]。

协方差矩阵R中的第m行、n列的元素可以表示为

分别取R中的第1 列和第1 行为参考元素，记为e1，e2：

对式(25)中的空间谱函数进行谱峰搜索，得到DOA估计值。

综上所述，本文方法的具体实现过程如下：

(1)根据式(3)构造信号协方差矩阵RX。

(2)设置交换矩阵J，根据式(12)构造新的数据接收矩阵Y(t)和协方差矩阵RY。

(3)根据式(14)得到新的协方差矩阵R。

(4)对R进行Toeplitz重构得到。

(6)对式(25)中的空间谱函数进行谱峰搜索得到DOA的估计值。

3 仿真分析

仿真实验中采用阵元数为8的均匀线阵，阵元间距为0.5 m，两个中心频率为1.5 kHz的远场窄带信号分别从0°和15°的方向入射到阵列。本文分别采用MMUSIC算法、RNSMUSIC算法、MUSIC算法以及本文方法进行DOA 估计。为了验证本文方法具有较高的分辨能力，将信噪比固定为0 dB，采样快拍数分别设置为200和50，图2、3给出了两个不同快拍数时的空间谱图。

由图2和图3可以看出，在信噪比为0 dB、快拍数为200时，MUSIC方法无法解相干，不能估计出两个相干信号，MMUSIC 方法、RNSMUSIC 方法和本文方法都可以成功分辨两个相干信号，但是本文方法的谱峰更加尖锐，旁瓣更低。在信噪比为0 dB，快拍数为50 时，MMUSIC 方法产生伪峰干扰，估计性能严重下降，RNSMUSIC 方法和本文方法可以成功分辨两个相干信号，并且本文方法估计性能更好。

图3 快拍数为50的DOA估计空间谱图Fig.3 Spatial spectrum of DOA estimation with 50 snapshots

将两个信号的入射角度分别设置为0°和7°，采样快拍数为200，其他仿真条件不变。图4 给出了四种方法的空间谱图。从图4可以看出，本文方法方位分辨力最好，方位估计精度最高。

图4 入射信号间隔较小时的DOA估计空间谱图Fig.4 Spatial spectrum of DOA estimation when the signal interval is small

将信号的入射角度分别设为0°、15°、25°，采样快拍数为200，其他条件不变，得到图5所示的空间谱图。从图5中可以看出，本文方法可以估计更多数目的相干源。

图5 信源个数为3时的DOA估计空间谱图Fig.5 Spatial spectrum of DOA estimation when the number of sources is 3

图6 三种方法分辨成功概率随信噪比的变化Fig.6 Variation curves of the success probabilities of three methods with signal to noise ratio

图7 三种方法分辨成功概率随快拍数的变化Fig.7 Variation curves of the success probabilities of three methods with the number of snapshots

图8 三种方法分辨成功概率随角度间隔的变化Fig.8 Variation curves of the success probabilities of three methods with the angle interval

从图6可以看出，随着信噪比的增加，信号的分辨成功概率也增加。在信噪比为3 dB 时，本文方法的分辨成功概率达到100%，与MMUSIC方法和RNSMUSIC 方法相比，可分辨信噪比分别降低了6 dB和8 dB，提高了空间方位分辨能力。

从图7可以看出，本文方法优于其他方法，在快拍数为50 时，本文方法的分辨成功概率能够达到86.5%，MMUSIC 方法和RNSMUSIC 方法的分辨成功概率分别为18.5%和40.5%。本文方法在快拍数为300 时，成功概率达到了100%，而MMUSIC 方法和RNSMUSIC 方法，在快拍数达到400时，成功概率依然在90%以下。因此，本文方法具有更高的稳定性，在快拍数较少时依然具有较好的方位估计性能。

从图8 可以看出，随着角度间隔的不断增大，三种方法的分辨成功概率也在不断增加。在入射角度间隔为8°时，本文方法的分辨成功概率能够达到100%，MMUSIC方法和RNSMUSIC方法的分辨成功概率分别为95%和97%，在角度间隔为12°时，这两种方法的分辨概率仍然低于100%。因此，本文方法在角度间隔较小时具有更好的分辨能力。

4 实验分析

本节对湖上实验的数据进行处理，验证本文方法在实际应用环境中的有效性。实验时，湖面布放两只实验船，发射船的头部和尾部分别悬挂两个发射换能器，发射同频率的CW脉冲信号，接收船吊挂一个5 个阵元的均匀水听器线阵接收声源信号，阵元间距按发射信号的半波长配置，两只小船的距离约为300 m，船长6 m，由几何关系可以分别推算出两个声源入射角度约为14°和20°。图9给出了湖上实验设备的位置示意图。

图9 实验设备布设图Fig.9 Layout diagram of test devices

从水听器采集的湖试数据中截取了20 000个样本数据，图10为5个阵元接收的数据结果图。分别采用本文方法、MMUSIC 方法、RNSMUSIC 方法以及MUSIC 方法对实验采集到的数据进行处理，得到的方位历程图如图11所示。

图10 阵元的实际接收数据Fig.10 The actual data received by the array

图11 四种方法的方位历程图Fig.11 Target orientation course charts obtained by four methods

从图11 中的4 个子图可以看出，本文方法在DOA 估计时充分利用了阵列接收数据，可以清楚地分辨两个相干信号。MMUSIC方法在DOA估计时则没有充分利用阵列接收数据，导致该方法无法成功分辨出两个相干信号。RNSMUSIC 方法在DOA 估计时虽然充分利用了阵列接收数据，但是由于信号入射角度间隔很小，无法分辨出两个相干信号。MUSIC 方法无法对相干信号进行解相干，不能有效地估计信号的DOA。从而验证了本文方法在相干信号DOA估计中的优异性能。

5 结论

本文提出了一种基于协方差矩阵Toeplitz 重构的MUSIC 算法的波达方位估计方法。该方法首先根据阵列接收数据的协方差矩阵及其翻转矩阵来构造新协方差矩阵，并利用新协方差矩阵构造To‐eplitz 矩阵，使阵列接收数据得以充分利用，然后通过MUSIC 方法进行空间谱估计。仿真和实验数据处理结果表明，与MMUSIC 方法、RNSMUSIC方法以及MUSIC方法相比，本文方法在低信噪比、少快拍以及入射角度间隔较小条件下的DOA 估计性能更好，并且能够对3个以上的多个相干信号进行精确的方位估计，在实际水下环境应用场景中也具有较高的方位分辨率和较好的方位估计性能，具有较大的工程应用价值。