低复杂度多输入多输出雷达目标角度估计方法

徐丽琴, 范 琳, 张 霞

(1.西安邮电大学 电子工程学院, 陕西 西安 710121; 2.西安邮电大学 计算机学院, 陕西 西安 710121)

多输入多输出(multiple input multiple output， MIMO)雷达利用多个发射天线发射相互正交的信号，在接收端利用多个接收天线对回波信号进行处理，通过匹配滤波分离出各个通道的信号。由于MIMO雷达拥有传统相控阵雷达不可比拟的优势，因此引起了国内外学者的广泛关注[1-2]。

波达方向(direction of arrival， DOA)估计是雷达参数估计的一个重要内容，其主要任务是从接收数据中提取目标的空间信息，实现对空间目标的检测和定位。近年来，有关MIMO雷达目标角度估计的研究取得了重要的进展[3-6]。多重信号分类(multiple signal classification, MUSIC)算法[7]和旋转不变子空间算法[8]是高分辨DOA估计算法的典型算法。其中，MUSIC算法适用于任意结构的阵列，但需要通过进行谱峰搜索来得到目标的角度估计，因此计算复杂度较高。文献[9]将MUSIC方法应用到MIMO雷达角度估计中，该方法涉及全维协方差矩阵的特征值分解，且需要在全角度范围谱峰搜索，导致其计算复杂度较高。文献[10]提出降低复杂度MUSIC算法(RC-MUSIC)，利用降维变换将接收数据降至低维空间，再利用MUSIC算法进行DOA估计，该方法虽然降低了矩阵运算维度，但仍需要在全角度范围进行谱峰搜索。文献[11]将半实值MUSIC方法应用到双基地MIMO雷达的角度估计中，该方法可将角度搜索区域减半，适用于任意阵列，但需要进行一维搜索，因此计算量仍然很大。文献[12]将多项式求根MUSIC方法运用到双基地MIMO雷达的角度估计中，避免了谱峰搜索，并且能实现DOA和DOD的自动配对，但当收发阵元数较大时，其运算量仍然很大。

为降低MUSIC算法的复杂度，本文提出一种用于单基地MIMO雷达目标角度估计的低复杂度降维求根MUSIC方法，该方法通过降维变换，将接收数据降至低维空间，然后在低维空间中通过导向矢量和噪声子空间的正交性，构造基于MUSIC的求根多项式，最后通过多项式求根代替谱峰搜索来获得目标的DOA估计。

1 信号模型

考虑由均匀等距线阵组成的单基地MIMO雷达系统，M个发射阵元和N个阵元接收阵元等间隔排布，假设阵元间距为半波长。在发射端，各发射阵元发射同频且相互正交的编码脉冲信号。假设远场存在P个不相关的目标，且目标距离远大于阵列孔径。在接收端，对接收到的回波信号进行匹配滤波并进行数据重排，可得接收数据[9]

x(t)=As(t)+n(t),

(1)

式中，A=[ar(θ1)⊗at(θ1),ar(θ2)⊗at(θ2),…,ar(θP)⊗at(θP)]∈MN×P为导向矢量矩阵，at(θp)=[1,ejπ sin θp,…,ej(M-1)π sin θp]T为发射导向矢量，ar(θp)=[1,ejπ sin θp,…,ej(N-1)π sin θp]T为接收导向矢量，θ1,θ2,…,θP分别为P个目标的方位角，“⊗”表示Kronecker积；s(t)=[s1(t),s2(t),…,sP(t)]T为目标反射系数矩阵；n(t)假设为高斯白噪声向量，其均值为零，方差为σ2。搜集L个快拍的接收数据，可得接收数据矩阵

X=AS+N,

(2)

式中，X=[x(t1),x(t2),…,x(tL)],S=[s(t1),s(t2),…,s(tL)]T,N=[n(t1),n(t2),…,n(tL)]T。

2 降维求根MUSIC算法

2.1 降维变换

在M个发射阵元和N个接收阵元所组成的MIMO雷达系统中，其虚拟通道数为MN个，接收数据的协方差矩阵维数为MN×MN维。若直接采用该数据矩阵进行DOA估计，则子空间估计所需的计算复杂度为O(M3N3)，其计算复杂度随着阵元数的增加呈立方次增长。为降低算法的复杂度，可采用降维变换将接收数据降至低维空间，使得后续的运算都是在低维空间中进行，可以大大减轻算法的运算量。

令zp=ejπ sin θp，则发射-接收联合导向矢量可以表示为

(3)

ar(θp)⊗at(θp)=Tg(θp),

(4)

导向矩阵A可以表示为

A=TG,

(5)

其中，G=[g(θ1),g(θ2),…,g(θP)]∈Me×P。

将式(5)代入式(2)可得

X=TGS+N。

(6)

从式(6)不难看出，信号位于由G张成的低维空间中。因此，可以构造降维变换矩阵，将接收数据降至低维空间，再进行目标的DOA估计，这样可以从整体上大幅度降低运算复杂度。为使降维后噪声方差保持不变，降维矩阵需选取为正交阵。此处，降维变换矩阵选取为U=W-1/2TH,其中

(7)

将降维变换矩阵U左乘接收数据矩阵X，可得

XT=W1/2GS+NT,

(8)

式中XT表示降维后的接收数据矩阵，NT=UN为降维后的噪声矩阵。

2.2 降维求根MUSIC算法

降维变换后，接收数据的协方差矩阵可通过下式进行估计得到

(9)

对式(9)进行特征值分解，可得

(10)

其中，Σs为由RT的P个较大特征值构成的对角矩阵，Es为由P个较大特征值对应的特征向量组成的信号子空间；Σn为由剩余的(Me-P)个小特征值构成的对角矩阵，En为与(Me-P)个小特征值对应的特征向量构成的噪声子空间。

根据导向矢量和噪声子空间的正交性，可以在低维空间中构造降维MUSIC谱为

(11)

传统的MUSIC算法通过搜索MUSIC空间谱的谱峰，进而得到目标的DOA估计。由于需要在全角度范围内进行谱峰搜索，导致计算复杂度较高。为进一步降低计算量，可在低维空间中构造基于MUSIC的求根多项式，再采用多项式求根代替谱峰搜索来获得目标的角度估计值。令

g(z)=[1,z,…,z(Me-1)]T，

则可以构造求根多项式为

(12)

求解该多项式的根，即可得到目标的DOA估计。

gH(z)Bg(z)=0。

(13)

若Bmn表示矩阵B的第m行第n列元素，则式(13)可改写为

(14)

θi=arcsin(angle (zi)/π)(i=1,2,…,P)

(15)

式中angle(·)表示取相位操作。

依据上述降维求根MUSIC算法，其实施步骤如下。

1) 构造降维矩阵U，左乘接收数据X，得到低维接收数据矩阵XT；

2) 计算XT的数据协方差矩阵RT，通过特征值分解估计得到其噪声子空间En；

3) 在低维空间中构造基于MUSIC求根多项式，计算多项式系数矩阵B；

4) 求解式(14)所示(2Me-2)阶多项式，得到(Me-1)对关于单位圆共轭对称根；

5) 寻找P个最靠近单位圆的根z1,z2,…,zP；

6) 根据式(15)获得目标的角度估计值θ1,θ2,…,θP。

3 计算复杂度分析

4 仿真实验

为了验证本文RC root-MUSIC算法的有效性，进行以下仿真实验来进行功能验证并与MUSIC算法和RC-MUSIC算法进行比较。仿真中，MUSIC算法和RC-MUSIC算法的角度搜索间隔为0.01°。假设单基地MIMO雷达系统的发射天线和接收线性均采用均匀线阵，各阵元等距分布且阵元间距为半波长。考虑位于方位θ1=10°,θ2=20°,θ3=30°的3个非相干远场目标。仿真进行500次蒙特卡罗实验，仿真结果取其统计平均值。用均方根误差

(16)

图1显示了MUSIC空间谱和RC-MUSIC空间谱及采用降维求根MUSIC算法得到的目标角度估计值。其中，发射阵元数M=8，接收阵元数N=6，快拍数L=20，目标信噪比为10 dB。从图中可以看出，RC-MUSIC谱比MUSIC谱具有更尖的谱峰和更低的旁瓣。同时可以看出，采用RC root-MUSIC算法，无需进行谱峰搜索，就可以精确地确定RC-MUSIC谱对应的谱峰位置，进而得到目标的DOA估计。

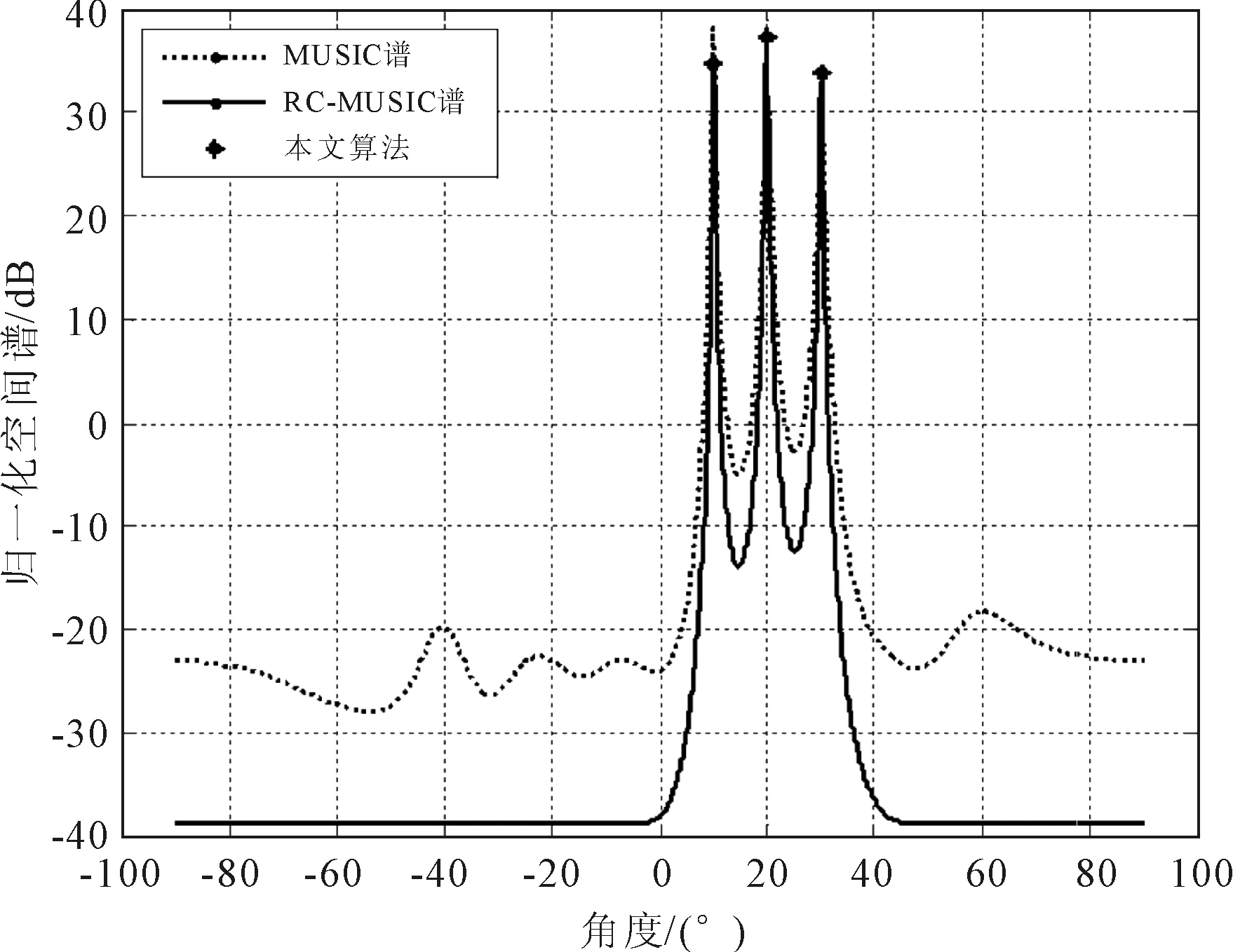
图1 MUSIC谱和RC-MSUIC谱比较

图2显示了在M=8,N=6,L=20条件下，用本文RC root-MUSIC算法进行100次仿真实验估计得到的3个目标的DOA。从图中可以看出，本文算法可以同时对多个非相干目标进行精确定位。

图3为角度估计的均方根误差随信噪比的变化的关系曲线。实验中，发射阵元数M=8，接收阵元数N=6，快拍数L=20，进行500次蒙特卡罗实验。从图中可以看出，在低信噪比区域，RC root-MUSIC算法可以获得比MUSIC算法和RC-MUSIC算法更高的估计精度。三种MUSIC算法的估计性能均随着信噪比的增加而提高，且具有相同的渐进估计性能。

图2 100次仿真实验角度估计值

图3 角度估计精度随信噪比变化关系

图4是在快拍数L=100，目标个数P=5，且假定收发阵元数相同情况下，3种算法的运算复杂度随阵元数的变化关系曲线。由图可见，降维求根MUSIC算法的计算复杂度比MUSIC算法和RC-MUSIC算法都低，这是由于该算法在低维空间中进行目标角度的估计，且避免了耗时的谱峰搜索，所以，算法复杂度大大降低。

图4 运算复杂度随阵元数变化关系

5 结语

提出了一种基于降维求根MUSIC算法的低复杂度单基地MIMO雷达目标角度估计方法。该方法采用降维变换降低接收数据的维数，在低维空间中构造旋转不变结构估计目标的DOA，算法通过多项式求根得到目标的角度估计，避免了谱峰搜索。仿真结果表明，与常规MUSIC算法和RC-MUSIC算法相比，该算法具有更低的运算复杂度，可以有效地提高MIMO雷达目标角度估计的速度，且在低信噪比条件下具有更高的角度估计精度。