冲激噪声背景下基于幅度预处理的测向新方法*
安春莲,张 玲,欧汉文,杨古月
(1.重庆文理学院 电子信息与电气工程学院,重庆 402160;2.吉林市轨道交通建设项目管理有限公司,吉林 吉林 132000;3.西南电子设备研究所,成都 610036)
0 引 言
传统的MUSIC算法和ESPRIT算法等波达方向(Direction of Arrival,DOA)估计算法大多考虑的高斯白噪声模型。然而,在很多实际应用模型中,具有冲激特性的非高斯噪声广泛存在,如水下噪声、无线信道噪声和各种人为噪声等,这类噪声被称为冲激噪声。可以使用特征指数α不同的SαS过程来对冲激噪声进行建模[3],由于冲激噪声不具备二阶及以上的矩,使得传统的测向算法在冲激噪声背景时往往失效[2-3]。因此,研究冲激噪声背景下的测向算法具有重要的理论价值和现实意义。
针对冲激噪声背景测向问题,研究人员提出了一系列新思路和新方法[4-6]。以分数低阶统计量为理论基础的分数低阶矩(Fractional Lower Order Moment,FLOM)类算法[4,7-8]则最初被提出,这类算法在弱冲激噪声时具有较好的估计性能,但在强冲激噪声时测向性能恶化严重。基于重构分数低阶协方差(Reconstructed Fractional Lower Order Covariance,RFLOC)的DOA估计方法[9]通过对分数低阶协方差矩阵进行重构,有效地改善了测向性能。但基于分数低阶协方差(Fractional Lower Order Covariance,FLOC)和FLOM都需要估计先验参数p,该条件难以满足且估计性能受参数p的影响较大。随后,基于稀疏理论和智能优化算法,一类通过多维寻优实现DOA估计的冲激噪声测向新方法被提出,在一定程度上对测向性能有所改善。但此类算法需要进行多维寻优,具有较大的计算量。随着研究的深入,冲激噪声测向的研究兴趣亦逐步向分布式信源[10]、宽带信号等测向领域扩展。通过对阵列接收数据的幅值上限进行估计和处理[5],能够有效去除噪声冲激性,使得二阶矩类测向算法可直接应用,具有计算相对简便且性能优良的特点,但是其预处理过程涉及先验参数设置,且在强冲激噪声背景的测向性能有待进一步提升。
综上所述,基于分数低阶统计量的方法在强冲激噪声情况时性能恶化严重,而基于稀疏理论或智能算法的方法往往又需要多维寻优,计算量非常大,能够直接使用二阶矩类测向算法的预处理方法计算简便,是值得研究的方向。本文通过对冲激噪声幅值特征进行分析,利用服从SαS分布的冲激噪声的分布统计特性,分别提出了基于阵列接收数据幅度均值和中值进行幅值预处理的方法,可对冲激噪声起到良好的平滑作用,使得传统基于二阶矩的测向算法能够直接应用。所提方法处理过程简单,计算简便,且估计性能优良,尤其是基于阵列接收数据幅度中值处理方法在低信噪比和强冲激噪声时都具有良好的估计性能。
1 数据模型
考虑N个窄带远场独立信号入射到阵元数目为M的均匀线阵上,阵列接收噪声服从标准SαS分布,则在t时刻的接收数据X(t)为
X(t)=AS(t)+N(t) ,
(1)
且
式中:A表示阵列流型矩阵;S(t)和N(t)分别表示t时刻的信号数据和噪声数据;xm(t)表示第m(m=1,2,…,M)个阵元的接收数据;a(θi)表示第i个信号的阵列导向矢量,且ui=e-j2πdcos θi/λ,d表示阵元间距,λ表示信号波长,i=1,2,…,N,θi表示第i个信号的入射角度。
服从SαS分布的随机过程没有固定的概率密度函数,因此常用特征函数对其进行描述:
φ(w)=e(jεw-γ|w|α)。
(2)
式中:α∈(0,2],为SαS过程的特征指数,用于描述SαS过程的冲激性,α取值越小,则噪声冲激性越强,当α=2时满足高斯分布;ε是概率密度函数的对称点,当α∈(1,2]时ε表示均值,当α∈(0,1]时ε表示中值;γ是分散系数(γ>0),类似于二阶过程的方差。
2 基于幅度预处理的测向新方法
2.1 经典的分数低阶统计量方法
经典的基于分数低阶统计量的测向方法有ROC、FLOM和FLOC。这三种方法所构造的分数低阶矩阵在第i行、第j列(i,j=1,2,…,M)上的元素分别为
(3)
(4)
(5)
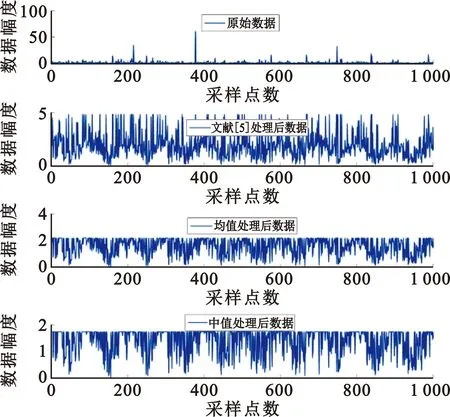
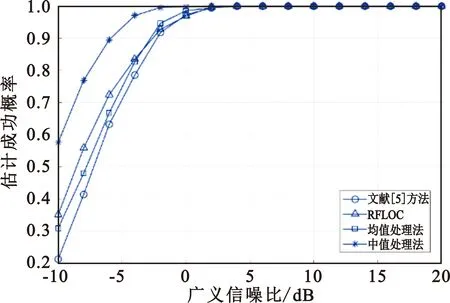
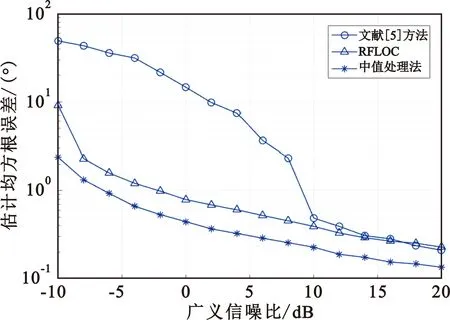
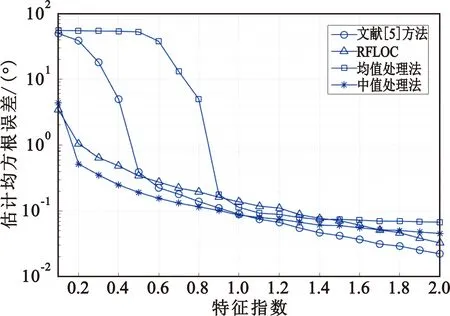
式(3)和式(4)中,1≤p<α≤2;式(5)中,0 从式(3)、式(4)和式(5)可以看出,这三种方法都要估计先验参数p,且p的取值对于测向结果有较大的影响。相较于二阶矩,基于分数低阶统计量的测向方法计算复杂度大大增加,还需要预估先验参数p,一般难以满足先验估计要求。因此,寻求适应强冲激噪声背景下基于二阶矩的测向方法具有重要的理论意义和实际应用价值。 由SαS过程的性质可知,其概率密度函数具有较大的拖尾,而且特征指数α取值越小,其拖尾就越大。这意味着,对于满足SαS分布的冲激噪声来说,其取得较大幅度的概率比高斯分布要高,从而体现出具有一定的冲激特性。特征指数α的取值越小,噪声产生大幅度值的概率也就越高,即冲激性越强。可见,冲激噪声的冲激性是随机的,其只在少数位置产生大的冲激信号,而在大多数没有冲激的位置,其幅值相对很小,只是无法预知其在什么时刻产生大的冲激。 在文献[5]中,作者提出了一种冲激噪声背景下对信号幅值上限进行估计的方法,然后依据幅值上限对阵列接收数据的幅值做截断处理。该方法能够有效削弱噪声冲激性,并直接使用二阶矩,避免求解分数低阶矩,计算量相对较低,且估计性能优于分数低阶统计量一类方法。但是,该方法中涉及可变参数的选取,给测向精度带来不稳定性。本文延续对阵列接收数据进行幅度截断处理的思想,基于对SαS过程特征的分析,提出了基于阵列接收数据幅度均值处理和基于阵列接收数据幅度中值处理两种方法。为了简便描述,分别将其简称为均值处理法和中值处理法。 根据SαS过程特征函数的描述,其位置参数ε是概率密度函数的对称点,当特征指数α∈(1,2]时,ε表示均值;当α∈(0,1]时,ε表示中值。可见,对于服从SαS过程分布的冲激噪声,其取得均值或中值的概率最大,冲激产生的位置是远离中值或均值的。因此,可以利用SαS过程幅值分布的这一特征对阵列接收数据进行幅值门限处理,从而去除大部分的冲激性。 (6) (7) 式中:i=1,2,…,M,函数sum(*)表示向量求和,函数med(*)表示求向量的中值。 然后,分别以Amean和Amed作为幅度门限,对阵列接收数据矩阵X(t)进行幅度门限预处理,其第i行、第t列(i=1,2,…,M;t=1,2,…,L)元素分别为 (8) (9) 处理后的阵列接收数据矩阵可进一步分别表示为 Xmean=AS+Nmean, (10) Xmed=AS+Nmed。 (11) 式中:Xmean和Nmean分别表示利用均值进行幅度预处理后的阵列接收数据和剩余的噪声成分,Xmed和Nmed分别表示利用中值进行幅度预处理后的阵列接收数据和剩余的噪声成分。 经上述幅度预处理所得阵列接收数据Xmean和Xmed中的噪声成分不再是冲激噪声,因而可以用基于二阶矩的测向方法实现DOA估计。无论是均值处理法还是中值处理法,其处理过程不需要额外的先验参数,只需根据阵列接收数据计算均值或中值。因此,与分数低阶统计量方法和文献[5]的方法相比,本文所提方法都具有处理过程简单、计算简便的优点。图1给出了广义信噪比为0 dB时,所提均值处理法和中值处理法以及文献[5]的方法在不同特征指数α下的阵列接收数据幅值和去冲激预处理后的数据幅值。 (a)α=1.5 (b)α=0.5图1 几种方法在不同特征指数时的处理效果 从图1可以看出,在弱冲激噪声时,均值处理法和中值处理法对于信号幅度上限的估计值比文献[5]的方法的估计值更小,也更为接近信号包络的幅度,这意味着本文所提出的幅度预处理方法能够滤除更多的冲激噪声,从而进一步提高DOA估计性能。随着噪声冲激性增强,即α∈(0,1]时,均值处理法对幅度估计的准确性严重恶化,文献[5]的方法也存在较大的性能退化,而中值处理法对幅度估计的准确性依然优良。由于SαS过程在α∈(0,1]时不存在有限的均值,因此在强冲激噪声背景下,基于阵列接收数据幅度均值的处理方法的估计性能恶化严重,而基于阵列接收数据幅度中值的处理方法对幅度上限的估计性能在弱冲激噪声和强冲激噪声时都具有优良的估计效果。 经过幅度预处理,已经有效地削除了噪声的绝大部分冲激性,可以直接利用幅度预处理后的阵列接收数据Xmean和Xmed求阵列数据协方差矩阵Rmean和Rmed: (11) (12) 式中:RS=E[SSH],表示信号数据协方差矩阵;Jmean和Jmed为M维矩阵,表示残余噪声的协方差矩阵。 (13) 且 (14) 本文通过仿真实验验证所提方法的有效性,将所提两种方法与文献[5]中的幅度处理方法和文献[9]中的RFOLC方法进行对比。仿真中采用阵元间距为半波长的8元均匀线阵,信号从0°~180°入射到阵列,冲激噪声满足标准SαS分布,快拍数为500,广义信噪比ρGSNR定义为 (15) 式中:E[|s(t)|2]表示信号功率。实验仿真中,RFOLC方法采用文献[9]中的方法构造数据矩阵。如无特别说明,仿真统计DOA估计成功概率时,当所估计的信号角度与实际信号角度的绝对值之差小于等于1°时认为估计成功。均方根误差的计算采用 (16) 两个窄带远场独立信号从35°和50°入射,进行500次独立试验,图2和图3分别给出了α=1.2和α=0.6时四种方法的估计性能随广义信噪比变化的曲线。其中,RFLOC参数p分别对应为0.4和0.2。 (a)估计成功概率 (b)估计均方根误差图2 α=1.2时估计性能随信噪比变化曲线 (a)估计成功概率 (b)估计均方根误差图3 α=0.6时估计性能随信噪比变化曲线 从图2可知,在冲激噪声不强烈时,本文提出的两种方法均优于文献[5]中的方法,从而验证了本文所提出的幅度预处理方法能够更好地消除冲激噪声。相同条件下,中值处理法具有最高的估计成功概率和最低的估计均方根误差,其他三种方法性能相差不大。结合图2和图3可以看出,随着噪声冲激性的增强,均值处理法完全失效,其他三种方法的估计性能存在一定的下降。图3中没有均值处理法,是由于其在此噪声环境下失效;文献[5]中的方法在低信噪比时估计均方根误差很大,这是由于在强冲激噪声和低信噪比时,其偶尔存在幅度门限估计偏差太大,造成估计失效引起的。RFLOC方法性能比较稳定,但估计性能相对中值处理法还有一定差距。由此可见,所提中值处理法能够有效改善低信噪比时的DOA估计性能,且对强冲激噪声的适应能力更好。 两个窄带远场独立信号从45°和55°入射,进行500次独立试验,广义信噪比为20 dB,图4给出了均值处理法、中值处理法、文献[5]中的方法和RFLOC方法的估计性能随特征指数α的变化曲线。 (a)估计成功概率 (b)估计均方根误差图4 估计性能随α变化曲线 从图4可以看出,本文提出的中值处理法具有最好的估计性能,即使在α=0.1时也具有较好的估计成功概率,进一步验证了其对强冲激噪声的适应能力;RFLOC方法对冲激噪声的适应性也较好,但不如中值处理法;文献[5]中的方法在强冲激噪声时估计性能严重退化。所提的均值处理法在α<0.7时几乎完全失效,在0.7<α<1时容易存在估计失效的情况,在α>1时与其他几种方法有相近的估计性能。 本文通过对SαS过程分布特性的分析,基于阵列接收数据幅度均值和中值,分别提出了均值处理法和中值处理法用于对阵列接收数据进行幅度预处理,从而平滑冲激噪声,可以直接使用传统的二阶矩进行DOA估计。所提均值处理法和中值处理法无需估计先验参数,且处理过程简单,具有较好的工程应用价值。均值处理法适用于α>1的弱冲激噪声环境,估计性能良好,但其在强冲激噪声背景下的测向性能还有待进一步提高。中值处理法性能优异,适用于α>0.1的强冲激噪声环境,可以有效改善现有方法在低信噪比和强冲激噪声环境下的测向性能。理论分析和实验仿真验证了所提方法具有良好的估计性能。2.2 SαS噪声幅度预处理方法


2.3 利用二阶矩进行DOA估计
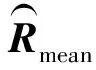

3 实验仿真与结果

3.1 不同信噪比时的估计性能


3.2 不同α时的估计性能

4 结 论

