高低腿输电铁塔分体式防护大板抗地表变形性能研究*

王新平 李志强 朱晓东 蒙春玲 舒前进 袁广林 李慧鹏

(1.中国能源建设集团山西省电力勘测设计院有限公司, 太原 030001; 2.中国矿业大学, 江苏徐州 221116)

0 引 言

输电铁塔基础形式的合理选择和科学设计,是确保煤炭采动影响区内的输电线路安全运行的关键问题,因此得到了学者们的重点关注。史振华针对采空区的输电铁塔,提出采用联合式基础代替原有的分裂式基础的技术措施[1]。山西省电力勘测设计院孙俊华提出了整体现浇式防护大板在采空区输电铁塔基础工程中的应用原则和技术措施[2]。代泽兵等对杆塔基础方案等提出了提高采空区特高压输电线路稳定性的技术措施[3]。袁广林等研究了典型单一地表变形作用下输电铁塔的破坏形态及其受力变形规律[4]。舒前进等通过试验和有限元模拟,研究了整体式防护大板对铁塔的保护作用,提出了大板合理厚度的取值方法[5]。此后,舒前进进一步研究提出了采动区输电铁塔整体式防护大板截面弯矩的函数表达式[6]。谭晓哲基于模型试验和有限元模拟,验证了开孔式复合防护板抗地表变形的有效性[7]。刘春城等分析验证了中空式混凝土复合防护大板的实用性[8]。张宏杰等依据实测沉降数据研究了沉降过程中铁塔的承载力状态,进一步验证了整体式复合防护板抵抗地表变形的有效性[9]。

近年来,我国对建设领域环保效益的要求越来越高,传统的整体式防护大板的土方开挖量大、容易导致水土流失等弊端日益突出,已无法满足山地边坡地带的铁塔基础的要求[10]。因此,研究山地线路铁塔新型抗变形基础具有重要意义。秦锋明等研究提出铁塔基础设计除了满足铁塔安全性外,还要充分考虑对周围环境的不利影响,选取合适的基础方案[11]。姜宏玺等提出了一种自平衡交叉铁塔基础,有效减少了基础工程造价[12]。钟维军等研究分析了输电铁塔板式基础、掏挖式基础和岩石嵌固式基础的技术经济指标,提出掏挖式基础和岩石嵌固式基础的技术经济指标更优[13]。吕振等提出了采空区35 kV输电铁塔“独立基础+槽型筏板”自适应新型基础[14]。此外,一些学者针对斜坡地区的线路,分析了长短腿铁塔及配套基础的方案。鲁先龙等提出了斜坡地带铁塔基础的设置方法[15]。薛乐研究提出了输电线路在山区工程所使用的长短腿铁塔及高低基础的配置优化方法[16]。侯晓燕等分析提出了以塔位桩为中心的高低腿杆塔接腿控制条件[17]。总体来说,传统的一体式防护大板技术方案在应用于陡峭山坡地带时,在造价、工期指标和生态保护等方面都无法取得令人满意的效果。目前,采用高低腿输电铁塔和配套的分体式防护大板,是解决传统一体式防护大板环保短板的可行方案,但其在采动区线路中的有效性还需要进行系统研究。

基于此,本文以典型220 kV线路中的高低腿输电铁塔为对象,以ABAQUS软件为工具,建立了高低腿铁塔、板柱基础、分体式防护大板和地基土的整体有限元模型,考虑塔腿级差(0,1,2,3 m)、分体式防护大板厚度(200,400,600 mm)、地表变形方向(0°,45°,90°,135°)等影响因素,分别模拟了不同方向的地表水平拉伸变形、水平压缩变形、正曲率变形和负曲率变形等4种单一地表变形的作用,分析获得了铁塔关键杆件轴力和塔脚(基础)相对位移,揭示了分体式防护大板对不同级差铁塔的保护效果。本文的研究结论,可为改进分体式防护大板的结构设计方法、促进该新型基础在采动区输电线路中的推广应用,提供参考和依据。

1 有限元模型及工况设定

1.1 输电铁塔及其基础概况

以某220 kV输电线路中的塔腿级差分别为0,1,2,3 m 的ZMC2猫头型自立式角钢直线塔为研究对象。该铁塔总高28.9 m,呼高21 m。级差为0 m时,铁塔顺线路、垂直线路方向的根开均为5.022 m。相应于0,1,2,3 m级差的铁塔结构示意见图1。不同级差的铁塔,仅两个短塔腿的高度和相应结构组成有区别,其他部分结构完全相同。

a—级差0 m; b—级差1 m; c—级差2 m; d—级差3 m。

图2示出了铁塔基础和防护大板的几何尺寸等信息。可见该铁塔的塔腿下方布置有混凝土现浇台阶式板柱基础。在两个高塔腿和两个低塔腿的板柱基础下方,各有一块矩形防护大板。这两块互相分离的大板称为分体式防护大板。大板内配双层双向直径12 mm、间距200 mm的HRB400钢筋。限于篇幅,图2中仅以级差为2 m、大板厚度为400 mm的情况作为示例。相关构件的组成关系参见图3b。本文分析时,考虑了防护大板厚度分别为0(无防护大板),200,400,600 mm。此外,在防护大板顶面和板柱基础底面之间,铺设100 mm厚的卵石粗砂垫层,以削弱板底土体变形的向上传递。

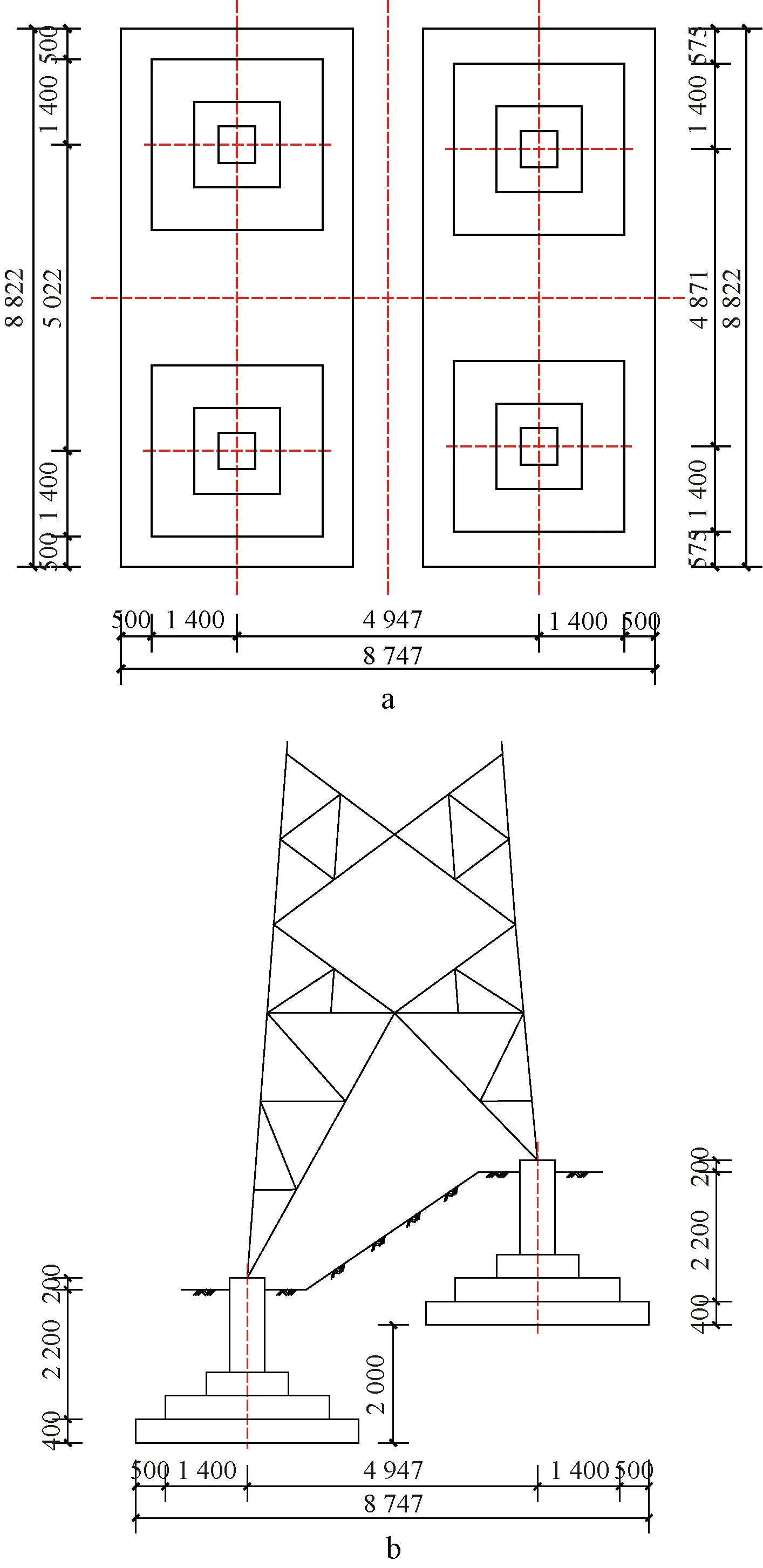
a—俯视图; b—侧视图。

a—整体模型(级差2 m); b—防护大板与板柱基础模型(大板厚200 mm)。

1.2 有限元模型的建立

基于ABAQUS软件建立有限元模型,原结构和基础单元选择、参数定义和网格划分简介如下。

1)铁塔结构。该铁塔杆件为Q235和Q345角钢,采用两结点空间线性单元B31模拟。其材料采用理想弹塑性本构模型,两种等级角钢的屈服强度分别定义为235 MPa和345 MPa,弹性模量均为2.06×105MPa,泊松比均为0.3。钢材密度为7.85×10-9t/mm3。

2)地基土。该铁塔位于山地边坡。模型的地基土的底部尺寸和周边尺寸对分析结果的准确性有一定影响。经过初步建模对比分析发现,当大板底部地基土的深度不小于板柱基础低阶宽度的5倍、板柱基础边界以外的土体水平尺寸不小于防护大板宽度的3倍时,铁塔结构内力等计算结果相对稳定。因此,最终模型中土体的平面投影尺寸为长30 m、宽30 m,厚度沿着坡度方向在9.62～30 m的范围内,见图3a所示。土体的模型单元是通过定义单元的几何尺寸来实现网格划分的。对于与板柱基础、防护大板交界的土体单元,定义其单个单元的边长不大于480 mm;对于其他区域,则定义单个单元的几何长度在480～1 600 mm之间自动划分。

铁塔基础周边原状土和回填土均为黄土,利用8结点六面体线性减缩积分单元C3D8R模拟,并采用摩尔-库伦屈服准则。土的内摩擦角ψ=30°,膨胀角ψ=0.1°,黏聚力c=0.1 kPa,弹性模量E=25 MPa,泊松比为0.25,密度为1.7×10-9t/mm3。

3)板柱基础和分体式防护大板。板柱基础、防护大板由C30混凝土和直径为12 mm的HRB400双层双向钢筋浇筑而成。对于混凝土,采用8结点六面体单元C3D8R模拟,密度、弹性模量、泊松比分别为2.5×10-9t/mm3、2.55×105MPa和0.167。混凝土单元的网格布置方式为“边布种”,单元尺寸为160 mm。对于板柱基础和防护大板中的钢筋,采用两结点线性单元T3D2模拟,具体方式为“内嵌”(图5),即不考虑混凝土和钢筋的黏结滑移。钢筋材料采用理想弹塑性本构模型,屈服强度、弹性模量、泊松比分别为400 MPa、2.06×105MPa和0.3。钢筋单元网格尺寸为20 mm。

4)接触界面。板柱基础和防护大板之间的滑动层、板柱基础和土之间的界面、防护大板和土之间的界面,均采用“面-面接触”进行模拟。对于混凝土构件与土之间的接触,摩擦系数、接触刚度、滑动黏滞阻力、最大许可应力分别为0.35、3×104kN/m3、25 kPa和17.65 kPa。对于板柱基础和防护大板之间的接触,摩擦系数、接触刚度、滑动黏滞阻力、最大许可应力分别为0.45、3×104kN/m3、0.25 kPa和0.25 kPa。

1.3 荷载、约束和地表变形的定义

1)荷载。研究重点为分体式防护大板的抗地表变形性能,而不是评估实际工程的安全性。因此,为了适当减少模拟工作量,对于上部荷载仅选择较简单的工况。定义铁塔荷载时,仅考虑15 ℃、无风情况下正常运行工况的相应荷载,即只考虑导地线及铁塔结构的自重,而不考虑覆冰、水平风荷载等。导线荷载、地线荷载、绝缘子自重分别为44.14,14.05,3.09 kN,分别施加在图4所示结点上。

图4 铁塔导(地)线荷载布置示意

2)约束。为了避免由于塔脚和基础连接结点的应力集中而导致计算难以收敛,建模时将塔脚分别和相应基础的顶面进行耦合,见图5a所示。板柱基础和大板中的钢筋是通过内嵌的方式与混凝土单元建立联系,见图5b所示。

a—塔脚和基础顶面耦合; b—基础内钢筋单元。

3)地表变形。经典的采煤沉陷理论认为地表变形可以分为地表水平拉伸变形、水平压缩变形、正曲率与负曲率等四种单一变形[4]。基于此,对每个分析模型仅考虑其中一种单一地表变形的单独作用,并考虑了每种地表变形沿着不同方向作用的情况。这里的变形方向,对于水平变形、曲率变形分别指地表移动方向、下沉等高线方向与铁塔顺线路方向的夹角α,包括0°、45°、90°和135°等四个方向,见图6、图7所示。需要说明的是,135°与45°方向垂直,为节约篇幅故未单独列出示意图。

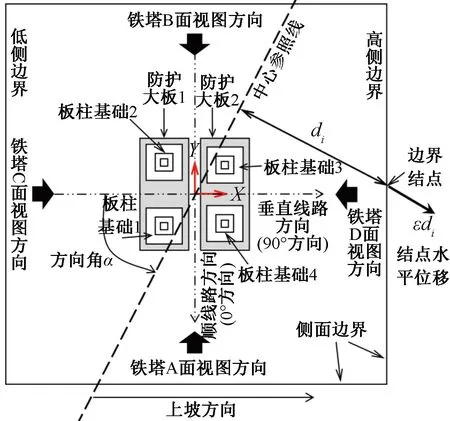
图6 地表变形方向角及有限元模型边界结点位移施加示意(俯视)

图7 地表变形施加示意

在有限元模拟中,地表水平拉伸变形、压缩变形是通过对地基土4个侧面边界的结点和土体底部结点施加指定方向的线位移来实现的,见图6、图7。位移方向垂直于图6所示的参照线(该线相应竖向截面的所有土体结点在指定方向的水平位移均为0),所有需要移动的单元结点的位移大小为水平变形值ε(mm/m)与该点到参照线的水平距离di(m)的乘积。本文分析时施加的水平地表变形值为ε=±20 mm/m[5]。

地表正曲率和负曲率是通过对地基土底部结点施加不均匀竖向位移来模拟的。假定在曲率变形作用下地基土底部结点位移为抛物线形状[4-5],且施加的底部曲率变形值为2.0 mm/m2。曲率变形的方向见图7所示。当模拟地表曲率变形时地基土4个侧面边界上的所有结点的水平位移均定义为0。对于正曲率变形(见图7底部虚线),底部结点的竖向位移值Zi=(0.000 1di)2。对于负曲率变形(见图7底部实线),土体底部结点竖向位移Zi=(0.000 1di)2-225。在这里,di为该结点到参照线的水平距离,mm。

1.4 分析荷载步的控制

计算分为4个步骤:1)杀死除地基土模型单元外的其他单元,针对地基土进行分析,获得相应的应力场和位移场;2)对地基土模型施加应力场,但位移场为零,作为模型的初始状态;3)激活步骤1)中杀死的模型单元,施加铁塔上的荷载,计算铁塔结构、地基土、板柱基础和防护大板的受力变形;4)施加相应的地表水平变形或者曲率变形,获得铁塔结构内力、板柱基础顶点(铁塔底部支座结点)水平位移等结果。

2 结果与分析

2.1 变形特征和破坏关键杆件

根据前述方法,分析获得了模型的受力变形。典型模型的铁塔受力变形情况和基础、地基整体变形如图8所示。图中仅以级差为2 m、板厚为200 mm的模型为例,展示了90°方向地表水平拉伸作用下的铁塔结构变形和应力分布情况以及整体模型位移云图。

a—铁塔应力云图,MPa; b—整体模型位移云图,mm。

模拟分析结果表明,在水平拉伸变形和正曲率变形下,铁塔根开变大,此时的铁塔相应面内的第一交叉斜材的受压,是判断铁塔是否破坏的关键杆件;反之,在水平压缩变形和负曲率变形下,铁塔根开变小,铁塔第二交叉斜材的受压,是判断铁塔整体安全状况的关键杆件。这与已有的关于等高腿铁塔的研究结论是一致的[4]。基于此,以各种地表变形作用相应的关键杆件轴力值和基础水平相对位移值为基础,分析获得铁塔设置分体式防护大板后的杆件内力和基础相对位移的减小幅度,并以此评估分体式大板对上部结构的保护作用。需要说明的是,为节约篇幅,本文仅对铁塔在各角度变形下最不利的两个基础间的相对位移进行了讨论。具体来说,当地表变形发生在0°、45°、90°和135°时,本文所述的基础相对位移分别是基础1和2之间、基础2和4之间、基础1和4之间、基础1和3之间,见表1所示。

表1 地表变形下基础相对位移和关键杆件轴力

模拟分析结果表明,在不同类型、不同角度的地表变形作用下的关键杆件存在明显的区别。比如,在0°拉伸或0°正曲率变形下,关键杆件是斜材C-XC-5;在45°拉伸或45°正曲率变形下,关键杆件是B-XC-5;在90°拉伸或90°正曲率变形下,关键杆件是A-XC-5;在135°拉伸或135°正曲率下,关键杆件是D-XC-5。在0°压缩或0°负曲率变形下,关键杆件是C-XC-7;在45°压缩或45°负曲率变形时,关键杆件是C-XC-7;在90°压缩或90°负曲率变形下,关键杆件是A-XC-7;在135°压缩或135°负曲率变形下,关键杆件是C-XC-7。上述杆件的位置和编号见图9所示。不同级差的铁塔在各地表变形下的关键杆件轴力值和基础水平相对位移值,列于表1中。

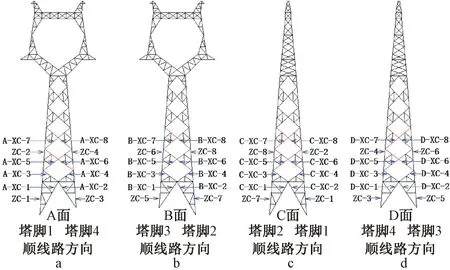
a—A面; b—B面; c—C面; d—D面。

为了定量评估分体式防护大板的保护作用,参考文献[5]的方法,以未设置防护大板(即大板厚度为0 mm)的模型为比较对象,分析当分体式防护大板厚分别为200,400,600 mm时的铁塔关键杆件轴力和基础水平相对位移的相对减小幅度,并据此评估分体式防护大板对于上部铁塔的保护效果。

2.2 铁塔支座(基础)相对位移

初步分析表明,在地表水平变形下,铁塔支座发

生的水平相对位移与地表水平变形的大小、方向密切相关。因此,分析铁塔支座水平相对位移的变化规律可以评估分体式大板的抗变形性能。限于篇幅,这里仅以0°地表水平拉伸变形为例,列出级差分别为0,1,2,3 m的铁塔的支座1和2的水平相对位移与地表变形的相关关系曲线于图10中。其他情况下,仅列出基础水平相对位移的变化幅度(相对于无大板模型),如图11～14所示。

a—级差0 m; b—级差1 m; c—级差2 m; d—级差3 m。—0 mm; —200 mm;---400 mm; —600 mm。

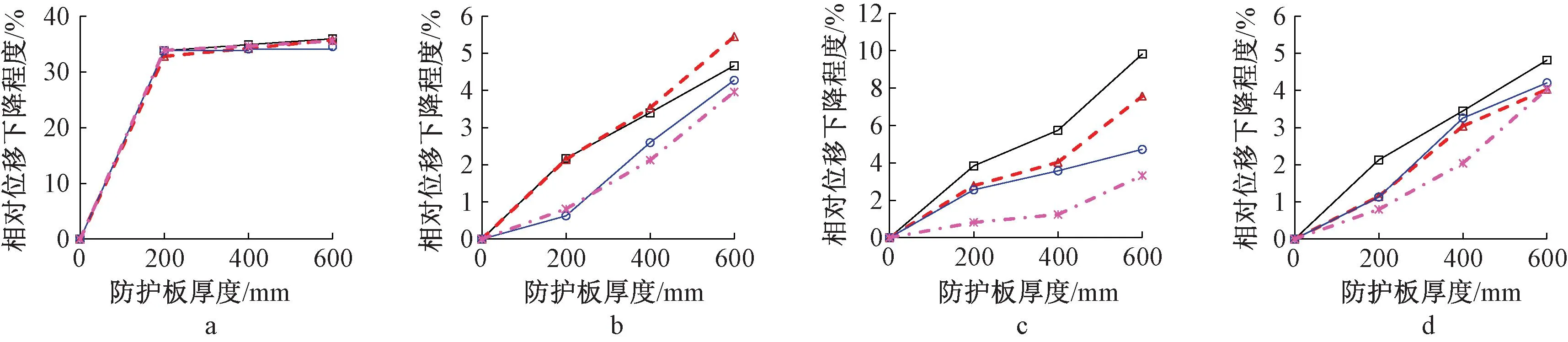
a—0°拉伸; b—45°拉伸; c—90°拉伸; d—135°拉伸。—0 m; ---1 m;—2 m; ---3 m。

由图10可见,无论是等高铁塔,还是塔腿级差分别为1,2,3 m的高低腿铁塔,随着地表变形从0逐渐增大到20 mm/m,支座1和2之间的相对位移呈线性增加的趋势。其中,在相同的地表变形下,以大板厚度为0(未设置防护大板)模型的相对位移最大,而设置有防护大板的模型的支座相对位移则小得多。对图10a～10d中的板厚为0的模型的等效地表水平变形进行线性拟合,得到的支座等效水平变形可分别表示为0.992 9ε、1.004 3ε、0.998 9ε、1.002 6ε。这说明,对于未设置防护大板的模型,无论其级差为多大,地表变形几乎大小不变的直接传递给铁塔基础,故容易因过大的地表变形而导致铁塔结构破坏。

以图10b为例,当铁塔级差为1 m时,根据板厚为0,200,400,600 mm的模型的支座相对位移值,可以计算得到等效地表变形值,经拟合得到的等效地表变形可分别表示为1.004 3ε、0.654 5ε、0.644 0ε、0.633 9ε。后三者与前者(1.004 3ε)的比值分别为65.2%、64.1%和63.1%,这表明大板将地表变形对铁塔的不利作用削弱了34.8%～36.9%,起到了很好的抗地表变形的作用。另一方面,板厚200,400,600 mm的三种厚度的防护大板对应模型的支座相对位移曲线非常接近,这表明在0°水平拉伸地表变形下,单纯增大防护板的厚度并不能进一步显著减小基础相对位移值。限于篇幅,其他方向、其他类型地表变形下的支座相对位移变化情况不再详细讨论,仅在后文讨论防护大板在不同方向和不同类型地表变形下对减小基础相对位移的保护效果。

图11～14分别示出了水平拉伸变形、水平压缩变形、正曲率变形和负曲率变形下的铁塔基础相对位移减小幅度(简称为保护作用)与防护大板厚度的关系曲线。

由图11、图12可见,在水平拉伸变形、压缩变形下,设置了分体式防护大板的模型的基础相对位移相对于无防护大板模型有显著降低,这表明分体式大板可以有效削弱地表变形向上部结构的传递。总体来说,在其他条件相同的情况下,板厚更大的模型,其基础相对位移的减小幅度更大。此外,在大多数的工况下,当板厚大于400 mm后,继续增大厚度所获得的保护作用增幅要小得多。这表明,当地表变形以水平变形为主时,兼顾保护效果和经济性的需要,将防护大板厚度设置为400 mm是比较合理的。

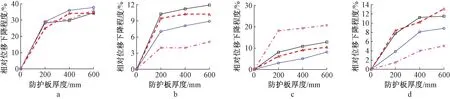
a—0°压缩; b—45°压缩; c—90°压缩; d—135°压缩。—0 m; ---1 m;—2 m; ---3 m。

由图13、图14可见,在曲率变形作用下,当其他条件相同时,板厚越大则铁塔基础相对位移的减小幅度越大,这与水平地表变形下的规律类似。有所不同的是,在曲率变形下,随着板厚的增大,防护大板的保护效果大致呈线性增大的趋势。

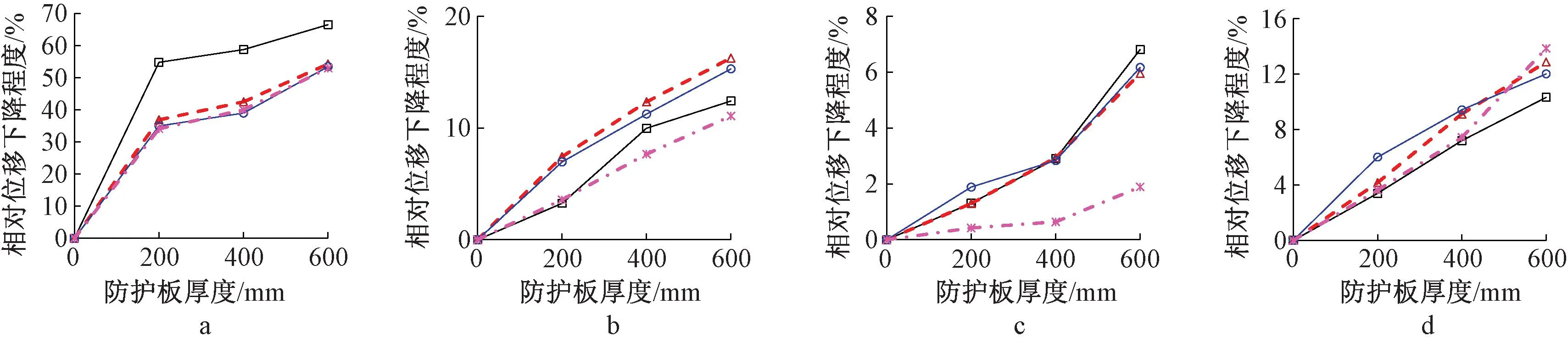
a—0°正曲率; b—45°正曲率; c—90°正曲率; d—135°正曲率。—0 m; ---1 m;—2 m; ---3 m。

a—0°负曲率; b—45°负曲率; c—90°负曲率; d—135°负曲率。—0 m; ---1 m; —2 m; ---3 m。

由图11～14还可见,分体式防护大板减小基础相对位移的效果与地表变形的方向密切相关。

在地表水平变形作用下,当地表水平变形沿着0°方向(顺线路方向)作用时,分体式大板的保护作用最大;当沿着45°、90°、135°方向作用时,保护作用则差得多。以级差2 m、板厚400 mm的模型为例,分体式大板在0°方向拉伸变形下的保护作用为34.2%,在45°、90°、135°方向拉伸变形下的保护作用分别为2.6%、3.6%和3.3%,后三者约为前者的1/10。同一个模型,分体式大板的保护作用在0°方向压缩变形下为36.0%,而在45°、90°、135°压缩变形下则分别为8.1%、5.1%和8.1%,均不到前者的1/4。这主要是因为,分体式大板的保护作用主要包括两个方面:一方面,由于分体式大板的连续性,可以分担水平方向的土体应力;另一方面,由于分体式大板和板柱基础间的滑动层,使得板柱基础的位移显著小于分体式大板周边土体的位移。因此,对于地表水平变形沿着45°、90°、135°方向作用的情况,由于分体式大板在这三个方向是不连续的,其对上部结构的保护作用,更多的依靠滑动层来实现,从而导致大板的保护作用比0°方向下更差。

在地表正曲率和负曲率作用下,与仅设置板柱独立基础的模型相比,设置了分体式防护大板的模型的关键杆件轴力都有明显的减小。在地表正曲率作用下,当地表变形沿着0°方向(顺线路方向)时,大板的保护作用最大;45°作用时次之,然后是135°作用时;而90°方向下的保护作用最差。在地表负曲率作用下,当曲率变形在0°方向(顺线路方向)时,大板的保护作用最大;135°次之,其后是45°方向;而90°方向下的保护作用最差。以级差2 m、板厚400 mm的模型为例,分体式大板在0°方向正曲率变形下的保护作用为38.8%,而在45°、90°、135°正曲率下分别为11.2%、2.8%和9.5%,仅为前者的7.2%～28.9%。同一个模型,大板在0°方向负曲率变形下的保护作用为33.2%,而在45°、90°、135°方向负曲率下分别为11.2%、1.4%和7.5%,同样远小于前者。这主要是因为在曲率变形下,分体式大板的弯曲变形能力是抵抗地表变形的主要决定因素。因此,对于地表曲率变形沿着0°方向作用时,大板的截面抗弯能力完全起到作用,因而大板及其以上部分(包括板柱基础、回填土)的总体曲率变形较小,使得不同板柱基础之间的顶点相对位移比无分体式大板的模型小得多。而对于沿着45°、90°、135°方向作用的情况,由于分体式大板整体上不连续,导致其整体协同抗弯效果较差,大板及其以上部分(包括板柱基础、回填土)的总体曲率变形相对0°工况下的变形更大,保护作用相对较差。

2.3 铁塔杆件轴力

图15示出了在0°方向地表水平拉伸变形作用下,铁塔斜材C-XC-5(见图9c)的轴力与地表变形值的关系曲线。可见:无论是等高铁塔,还是塔腿级差分别为1,2,3 m的高低腿铁塔,随着地表变形从0逐渐增大到20 mm/m,斜材C-XC-5的轴力呈线性增加的趋势。其中,在相同的地表变形下,以大板厚度为0(未设置防护大板)模型的杆件轴力最大,而设置有防护大板的模型的杆件轴力则小得多。以图14b为例,当铁塔级差为1 m时,根据板厚为0,200,400,600 mm的模型的杆件轴力与地表变形的关系曲线,从数值上轴力可分别表示为1.501 7ε、1.012ε、0.994 1ε、0.960 7ε,后三者与前者的比值分别为67.4%、66.2%、64.0%,这表明大板的存在将地表变形引起的杆件轴力降低了32.6%～36.0%,对上部铁塔结构起到了良好的保护作用。由图15还可见,板厚200,400,600 mm三种厚度的大板对应模型的杆件轴力曲线非常接近,这表明在0°水平拉伸地表变形下,单纯增大防护板的厚度无法进一步显著提高防护大板的抗变形性能。限于篇幅,其他方向、其他类型地表变形下的关系曲线不再详细讨论,仅在下文讨论防护大板在不同方向和不同类型地表变形下对减小杆件轴力的保护作用。

a—级差0 m; b—级差1 m; c—级差2 m; d—级差3 m。

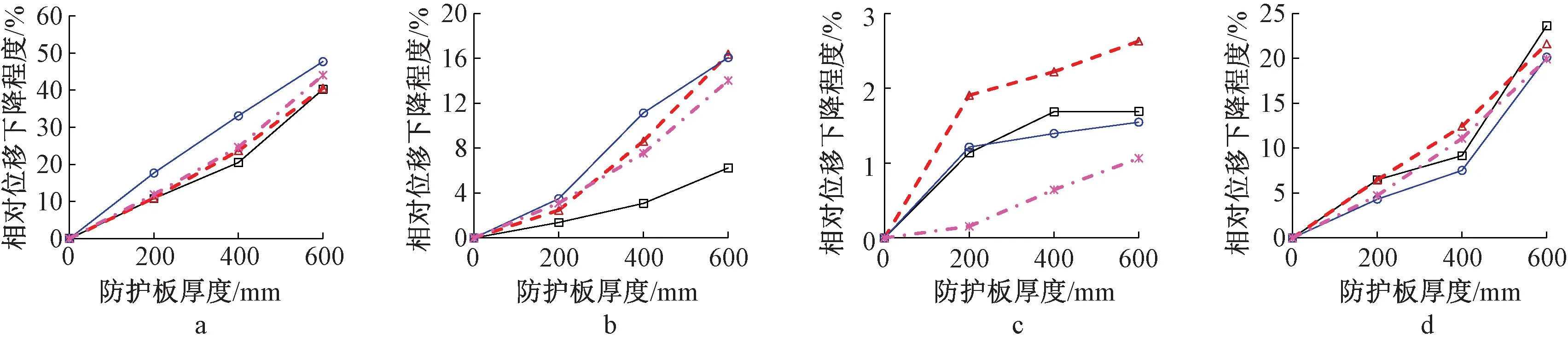
图16、图17分别示出了地表水平拉伸变形和水平压缩变形下铁塔关键杆件轴力的减小幅度(保护作用)与分体式防护大板厚度的关系曲线。

a—0°拉伸(C-XC-5); b—45°拉伸(A-XC-5); c—90°拉伸(A-XC-5); d—135°拉伸(C-XC-5)。

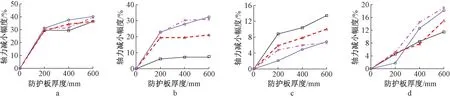
a—0°压缩(C-XC-7); b—45°压缩(D-XC-7); c—90°压缩(A-XC-7); d—135°压缩(C-XC-7)。

可见:在地表水平变形作用下,与无防护大板的模型相比,设置分体式防护大板的铁塔的关键杆件轴力均明显减小。杆件内力的减小程度(大板对铁塔的保护作用),与地表水平变形方向密切相关;当

水平变形角度为0°方向(顺线路方向)时,无论是拉伸变形还是压缩变形,杆件轴力减小幅度都在30%左右甚至更大,说明此时大板对铁塔的保护作用很明显;当水平变形角度为90°时,杆件轴力减小幅度相对最小,大部分小于10%;当水平变形角度为45°和135°时,杆件轴力的减小幅度总体上介于前两者之间。以级差2 m、板厚400 mm的模型为例,在水平拉伸变形作用下,当角度为0°时杆件内力下降幅度为34.4%;当角度为90°时,下降幅度为5.6%;而当角度为45°、135°时,下降幅度分别为8.4%、8.6%。同一个模型,在水平压缩变形作用下,当作用角度为0°时杆件内力下降幅度为37.7%;当作用角度为90°时,下降幅度为4.7%;而当作用角度为45°和135°时,下降幅度分别为27.9%和12.5%。这表明,分体式大板在0°地表水平变形下效果最好,而在90°水平变形下效果最差。这主要是因为,在90°方向上,分体式大板是完全分离的,其对地表变形向上传递的抵抗(削弱)完全依靠板柱基础和大板之间的滑动层,大板无法有效分担变形方向的地基应力,因而效果相对最差。

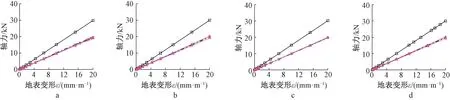
图18、图19分别示出了正曲率变形和负曲率变形下的铁塔关键杆件轴力的减小幅度与大板厚度的关系曲线。关键杆件的编号及位置见2.1节所述。

a—0°正曲率(C-XC-5); b—45°正曲率(A-XC-5); c—90°正曲率(A-XC-5); d—135°正曲率(C-XC-5)。

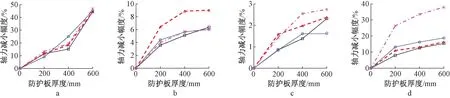
a—0°负曲率(C-XC-7); b—45°负曲率(C-XC-7); c—90°负曲率(A-XC-7); d—135°负曲率(A-XC-5)。

可见:在地表曲率作用下,与未设置防护大板的模型相比,含分体式防护大板的模型的铁塔关键杆件轴力均明显减小,且减小幅度与地表变形方向密切相关;相比其他角度,当地表曲率沿着0°方向(顺线路方向)作用时,关键杆件轴力下降幅度最大,分体式大板的保护作用最好;而当曲率变形角度在 45°、90°和135°时,除了135°负曲率工况的模型和45°正曲率工况的级差为1 m的模型,其他大部分模型的杆件轴力下降幅度都相对较小。比如,45°方向

下,除了级差为1 m的铁塔杆件下降幅度超过15%外,其他模型和工况下的轴力下降幅度都明显小于10%;对于135°正曲率工况,大部分模型的杆件轴力下降幅度都小于10%;90°曲率工况下模型杆件轴力下降幅度大部分都小于5%;其中,负曲率变形下的降低幅度几乎可以忽略不计。总体来说,地表发生曲率变形时,当分体式大板方向与地表曲率方向一致时,对上部结构保护效果最好;当分体式大板方向与曲率方向垂直时,对上部结构保护效果最差;当大板方向与曲率变形方向斜交时,对上部结构仍有一定的保护效果。这说明,在线路规划时应对未来地表变形的大小和方向进行预计,然后使分体式防护大板的长度方向与水平变形、曲率变形的方向尽量一致,以充分发挥分体式防护大板的抗地表变形能力。

由图16～19还可见,在相同条件下,更大的板厚带来更明显的杆件内力降低效果,对上部铁塔具有更好的保护作用。除了45°拉伸(图16b)、0°正曲率(图18a)、90°正曲率(图18c)和0°负曲率(图19a)四种变形作用的情况外,其他模型对应的曲线呈现出“大板对铁塔内力的减小效果随着板厚的增大先明显增大,而后当厚度达到400 mm后增大幅度显著趋缓”的特征。这说明,仅本文的研究范围来说,当大板的厚度大于400 mm后,继续增大板厚的总体经济性呈现下降趋势。因此,从减小铁塔结构内力的角度来说,该铁塔无论级差为多少,采用400 mm作为分体式大板的厚度是兼顾保护作用和经济性的最好选择。

3 结 论

1)与仅采用板柱式独立基础相比,设置分体式防护大板能够有效降低高低腿输电铁塔杆件轴力和基础(支座)相对位移,对上部铁塔结构起到良好的保护作用。

2)分体式大板的抗地表变形性能与地表变形的作用方向密切相关。当地表水平变形和曲率变形的方向与大板长度方向一致时,分体式大板的抗地表变形作用最明显,在地表水平拉伸、水平压缩、正曲率和负曲率变形下可分别减少铁塔内力的34%、30%、23%和12%。而当地表变形方向与大板宽度方向一致时,大板的抗变形性能最弱,在各种地表变形下的保护作用总体在10%以下。

3)分体式防护大板对铁塔的保护效果随着板厚的增加而逐渐提高。总体来说,当板厚达到400 mm之后,大板的保护作用随着板厚的增加而增大的趋势不再明显。因此,在设计分体式防护大板时,推荐采用400 mm的厚度。

本文的结论是针对典型铁塔及其基础、大板分析得出的,在进一步推广应用分体式防护大板时,还需要结合更多输电线路的实际情况,开展系统深入的研究,对分体式大板的结构设计方法和应用原则提出更全面的改进措施。