网架结构特征值屈曲分析的数值方法*

乐风江 杨富儒 方希兵 赵 文

(1.新疆大学建筑工程学院, 乌鲁木齐 830047; 2.新疆大学,新疆建筑结构与抗震重点实验室, 乌鲁木齐 830047;3.武汉理工大学土木工程与建筑学院, 武汉 430070)

0 引 言

长期以来,网架结构特征值屈曲分析均利用杆单元模型或不分段梁单元模型进行数值分析,杆单元和不分段的梁单元模型符合空间结构的物理概念,每一根杆件划分为一个单元的分析契合工程设计的理念。近年来的研究[1]指出杆系结构稳定分析时,采用梁单元若不考虑分段(包括杆单元)时其误差较大,可采用提高形函数的阶次来提高解的精度。在网壳结构稳定性的研究中更是提出了采用多段梁单元模型的数值方法,认为采用多段梁模型不仅可以提高解的精度还可以引入缺陷考虑杆件屈曲[2-5],同时该方法也在网架结构分析中得以应用[6]。空间网格结构稳定性分析中若不考虑杆件失稳会高估结构的承载能力,但文献中并未讨论采用多段梁合理性的说明,使得在网格结构稳定分析中单元选用缺乏相对依据。为此,讨论了杆单元与梁单元在空间网架特征值屈曲分析中的问题,进一步论证和揭示多段梁单元模型用于空间网架结构特征值屈曲分析和稳定分析的正确性及内在机理,提出了网架结构特征值屈曲数值分析的方法。

1 铰支受压杆的屈曲分析

1.1 铰支受压杆屈曲分析的近似解

图1为理想铰支受压杆等截面直杆,其上所受轴心压力P作用,求解得临界荷载[7]为:

图1 铰支受压杆

(1)

式中:n为系数;I为截面惯性矩;E为弹性模量;l为柱高。

当n=1时,其临界荷载(解析值)为:

(2)

相应的挠曲线为半波正弦函数。当n=2,3,…时,压力P为解析值的4倍、9倍等。

1.1.1瑞利-里兹法

由势能驻值原理得铰支受压杆的势能表达式:

(3)

式中:v为挠度。

当体系处于平衡状态时,其总势能一阶变分为零,即:

δΠ=0

(4)

设定不同的挠度曲线方程v=v(x)将得出不同的解。对于两端铰接受压杆[8],有以下3种情况。

1)设v=ax2+bx+c,求得临界荷载:

(5)

其值与解析值的误差约为21.6%,且所设变形曲线不够理想。

2)设以均布荷载q作用下梁的变形曲线作为屈曲时的近似变形曲线,即:

(6)

求得临界荷载:

(7)

其值与解析值相比,误差约为0.13%。

(8)

其值与解析值相同。

由瑞利里兹法求解所得的临界荷载的精度取决于变形曲线,实质为位移函数。当位移函数越接近解析解的挠曲线时,其结果也越精确。

1.1.2有限单元法

有限单元法是将里兹法“结构化”或“格式化”,即通过构造位移函数(通常较为简单)形成单元刚度矩阵和应力刚度矩阵来求解相应问题。运用有限元法求解铰支受压杆,其构造的位移函数为[7]:

v=A+Bx+Cx2+Dx3

(9)

单元分段不同,临界荷载的计算式不同。

1)将单元分为2段,临界荷载为:

(10)

2)将单元分为4段,临界荷载为:

(11)

由式(10)、(11)可知,两式与式(2)的误差已经较小,且分段数目越多,结果会越接近精确解。一般情况下,单元分段数量为3～5时,精度就能满足要求。

1.2 铰支受压杆的屈曲分析

特征值屈曲分析中,需求解其特征值方程[9]:

[KE]+{λi}[KG]){φi}=0

(12)

式中:[KE]为弹性刚度矩阵;[KG]为几何刚度矩阵,或称为初始应力刚度矩阵;{λi}为第i阶特征值;{φi}为与{λi}对应的特征向量,是相应该阶屈曲荷载时结构的变形形状,即屈曲模态。在ANSYS的特征值屈曲分析中,其结果给出的是{λi}和{φi},即屈曲荷载系数和屈曲模态,而屈曲荷载为{λi}{P0}。

采用Link 180单元分析铰支受压杆,由于杆无侧向位移,不能形成几何刚度矩阵,无法进行特征值屈曲分析。设受压杆采用圆钢管,参数如表1所示,试采用Beam 188(梁单元)进行分析。

表1 圆钢管参数(60 mm×3.5 mm)

由表2可知,Beam 188单元选用不同的形函数[10]时,单元形函数阶次越高,单元数目划分较少(3～5段)即可得出较为准确的最低阶屈曲荷载系数。若不考虑单元分段,形函数阶次的选择直接影响几何刚度矩阵和弹性矩阵的形成,一次形函数的精度不如二次形函数。

表2 铰支受压杆最低阶屈曲荷载系数

由图2～图4可知:分段数目越多,屈曲模态越接近“半波正弦函数”。若单元不考虑分段,不论采用哪种形函数,铰支受压杆均不会发生屈曲,其屈曲模态为直杆。这是因为若仅采用一个单元,其杆件中间无节点位移,屈曲模态上无法显示出“半波正弦曲线”,当杆划分为多个单元时(3段或5段),铰支受压杆中间节点有位移,其形状虽不是光滑的“半波正弦曲线”,但随着单元划分数目的增多,屈曲模态愈接近“半波正弦曲线”(铰支杆划分50段时最低阶屈曲模态已经非常接近,但在实际工程分析时,不需要划分这么多单元)。

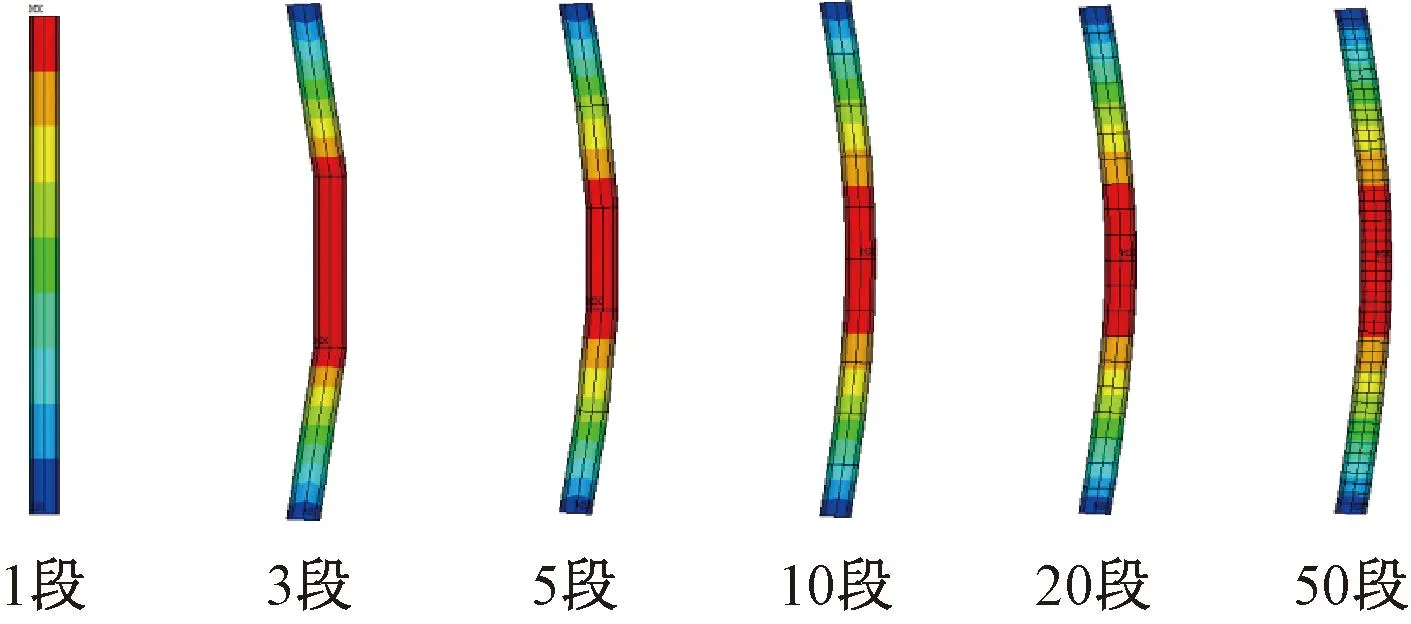
图2 Beam 188单元采用一次形函数时不同分段数目的最低阶屈曲模态

图3 Beam 188单元采用二次形函数时不同分段数目的最低阶屈曲模态

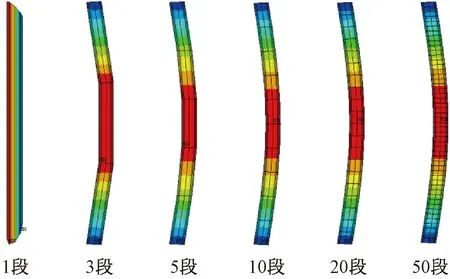
图4 Beam 188单元采用三次形函数时不同分段数目的最低阶屈曲模态

有限元分析的解与理论解存在误差的原因是,一方面由于形函数本身存在误差,这种误差可以通过将单元分段来减小;另一方面,Beam 188是空间(3D)梁单元,而理论解是由平面梁得到的,其支座约束条件与平面铰接条件有一定差别。

2 铰接桁架的屈曲分析

2.1 铰接桁架屈曲分析的解析解

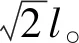
(13)

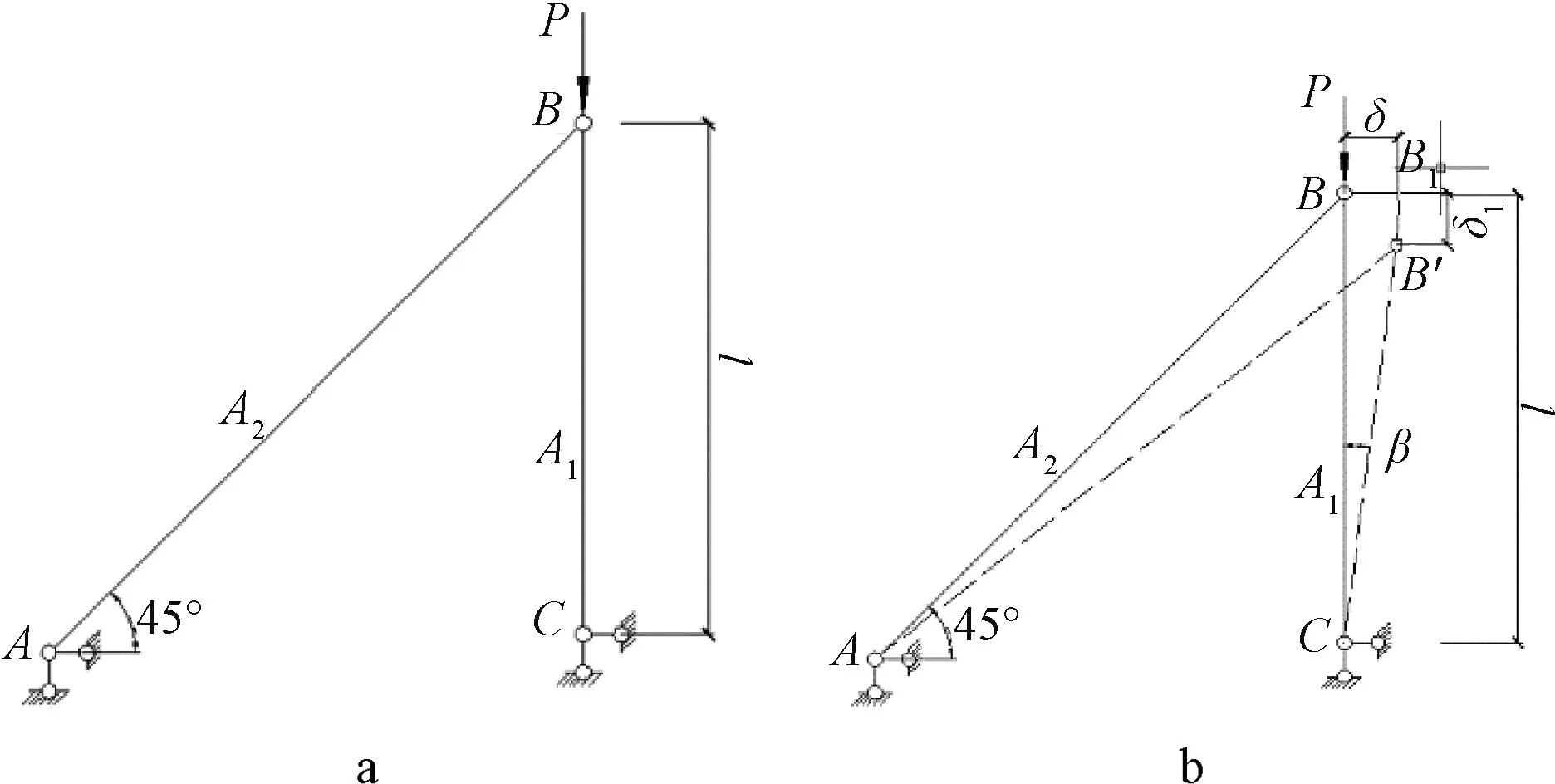
a—铰接桁架; b—铰接桁架节点失稳示意。

临界荷载Pkp必须小于将BC杆视为两端铰支时的临界荷载才有实际意义。否则,体系将是由于BC杆的屈曲丧失稳定而不是由于节点B发生横向侧移而失稳。它应满足:

(14)

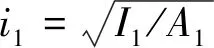
式中:i1为回转半径。

当两杆弹性模量E相同时,上述条件可以表示为:

(15)

一般(i1/l)2很小,故当A2远小于A1或α角很小时,才会发生B点横向侧移而失稳[8]。以上给出的结论实际上基于杆单元的桁架整体失稳的解析式,并不考虑杆件屈曲。

2.2 铰接桁架屈曲分析的有限单元解

采用杆单元求解铰接桁架的屈曲荷载系数[11]:

(16)

其中φ=A1/A2

令N=1,φ=1,即A1=A2,得:

(17)

基于杆单元进行求解时杆件不发生屈曲,λcr只与杆件的截面面积和弹性模量以及两杆的相对长度有关,与其绝对长度和截面惯性矩无关,不符合屈曲理论[11]。

2.3 铰接桁架的屈曲分析

2.3.1采用Link 180单元的铰接桁架屈曲分析

令:A1=A2=6.212 5×10-4m2,取E=200 GPa,则ANSYS分析结果为λcr=-3.244 6×107。

选用Link 180单元,其屈曲荷载系数与有限元法采用的杆单元的结果一致,其屈曲模态(图6)表现为铰接桁架结构节点侧移而使结构失稳,但此临界荷载作用下,杆件所受应力可能远远超过屈服强度,且不能反映杆件屈曲。

图6 采用Link180单元的屈曲模态

2.3.2采用Beam 188单元的铰接桁架屈曲分析

由表3和表4可以看出,采用Beam 188单元时,若梁单元不考虑分段,随着形函数的阶次提高,其屈曲荷载系数也越接近准确值(λcr=-71.675),但屈曲模态均不能反映杆件失稳;若梁单元考虑分段,其屈曲模态可以反映杆件失稳。

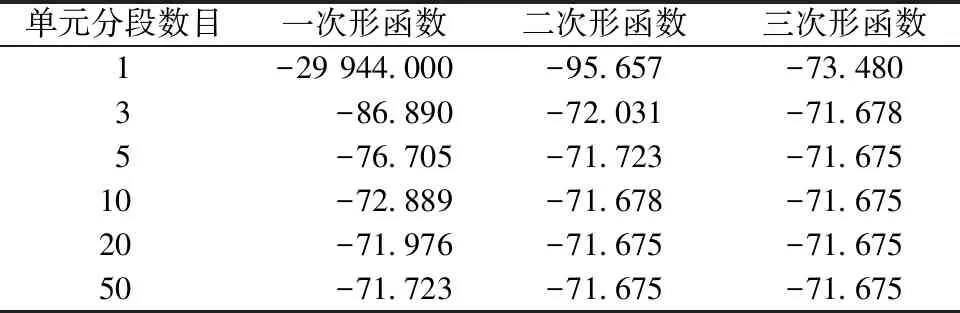
表3 铰接桁架最低阶屈曲荷载系数

表4 Beam 188单元采用不同形函数及不同分段数目的最低阶屈曲模态

在形函数不变的条件下,单元分段的数目越多,其结果越准确;形函数阶次越高,分段数目较少时即可得到较为准确的解。

3 网架结构特征值屈曲分析

网架平面尺寸为22.4 m×34 m,高度1.6 m。网架屈曲分析时荷载组合选用:1.2×恒载+1.4×活载。网架结构杆件截面由满应力优化设计获得,杆件截面规格和框架梁柱尺寸见表5所列。单一网架分析时,支座采用固定铰支座;考虑下部框架时,由于实际工程中,网架与框架支座一般采用平板钢支座,其刚度一般较大[12]。ANSYS分析时,网架采用梁单元,框架采用实体单元,两者的连接采用“刚性区法”[9]。

表5 网架截面规格和框架梁柱尺寸

3.1 单一网架的特征值屈曲分析

3.1.1采用Link 180单元的特征值屈曲分析

采用Link 180单元进行数值模拟分析,得到屈曲荷载系数为λcr=-84.894,其屈曲模态如图7所示。其临界荷载过大是由于杆单元无法考虑杆件屈曲而高估网架整体稳定性所致。

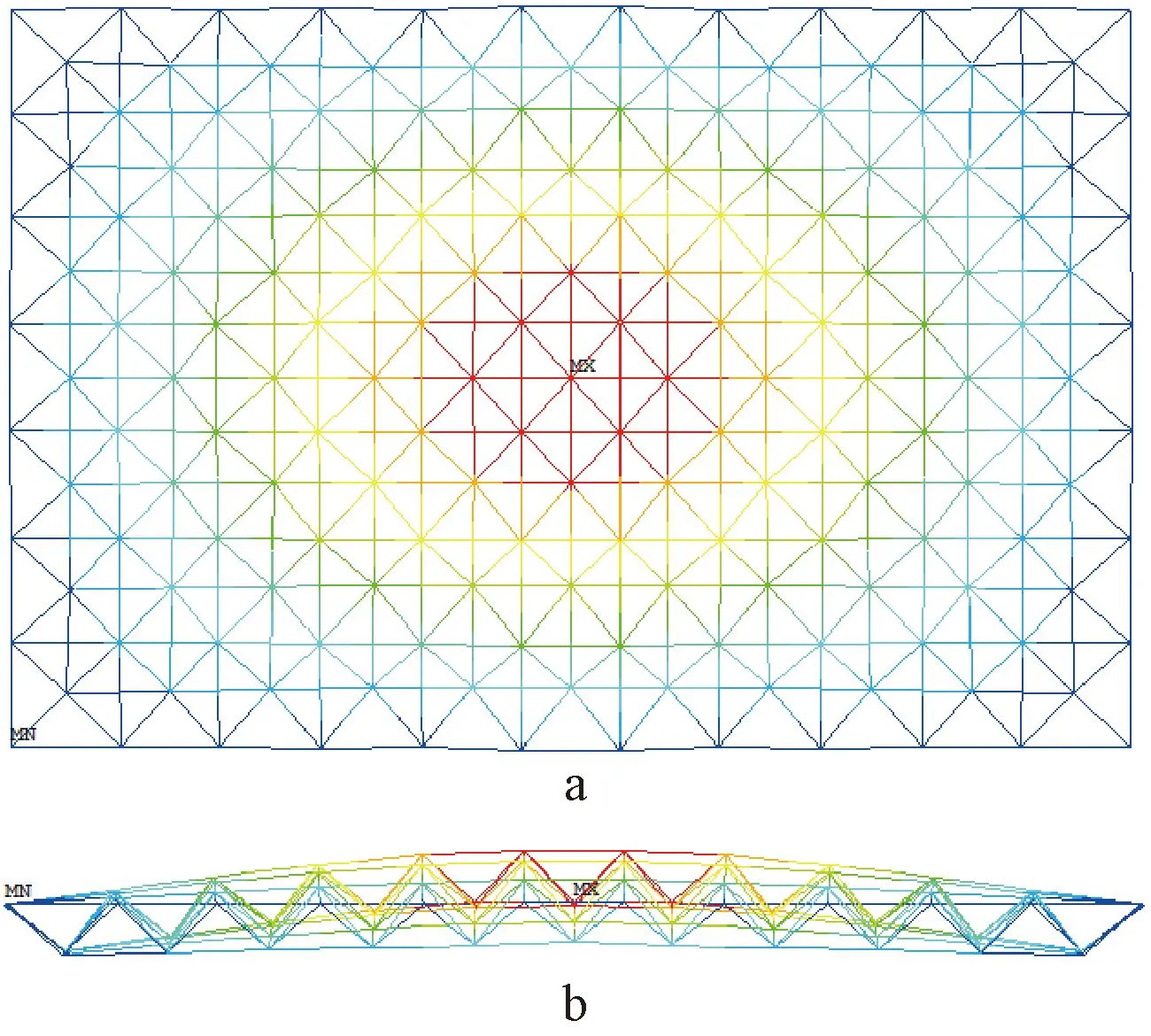
a—平面图; b—侧视图。

3.1.2采用Beam 188单元的特征值屈曲分析

由表6及图8、9可知,Beam 188单元选用一次形函数且不考虑分段的最低阶屈曲荷载系数为-86.312,屈曲模态无法反映杆件屈曲,对比分段的结果为-1.609 4(分段数目为50),网架的屈曲模态可以反映出杆件失稳。

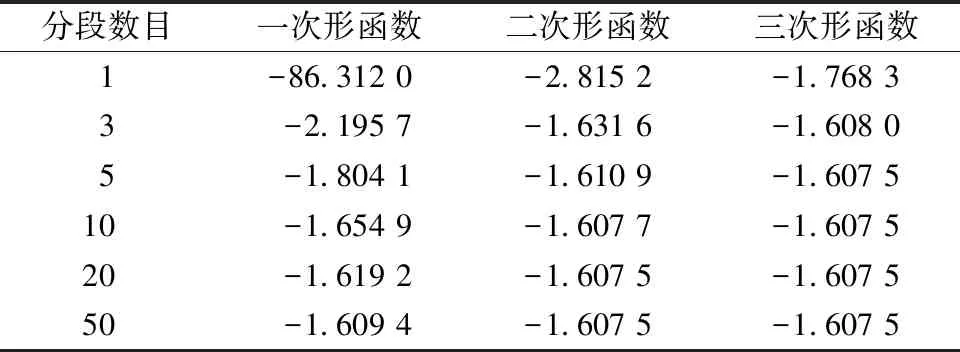
表6 单一网架的最低阶屈曲荷载系数

a—平面图; b—侧视图。

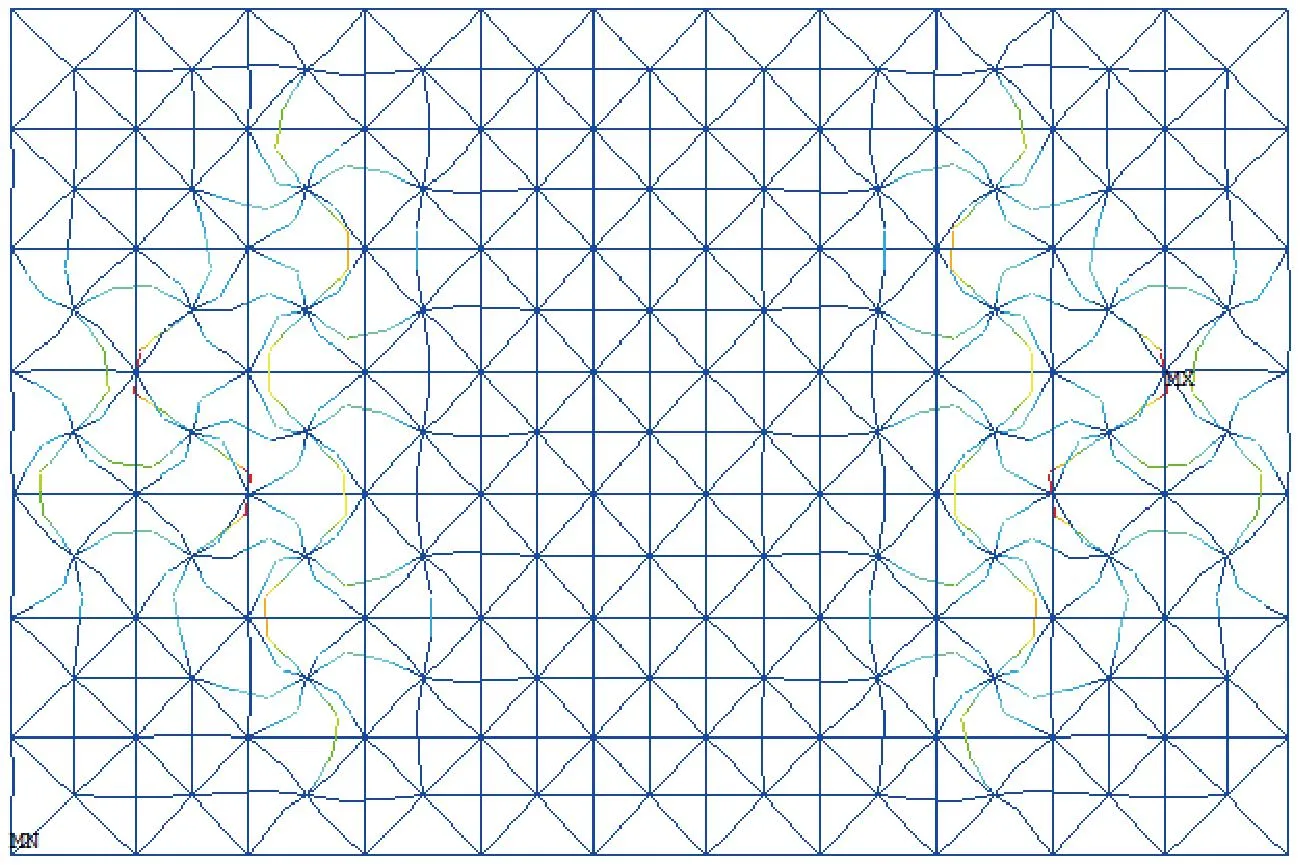
图9 选用一次形函数、分段数目为3时网架的最低阶屈曲模态

由图10、11所示,当Beam 188单元采用二次或三次形函数时,若考虑不分段,最低阶屈曲荷载系数虽已较为接近精确值,但屈曲模态仍不能反映杆件失稳;考虑分段之后,网架可以反映出杆件失稳。

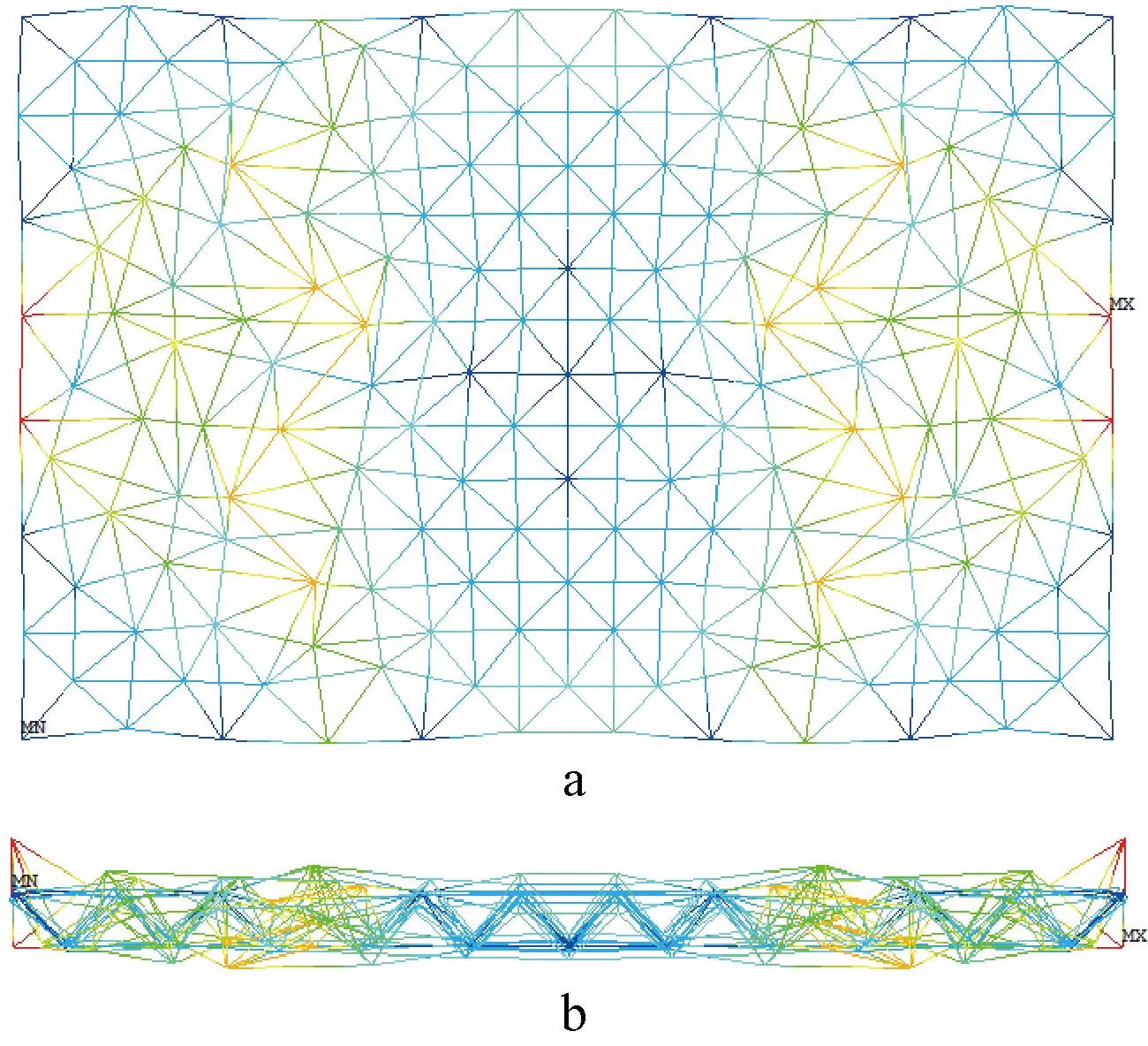
a—平面图; b—侧视图。

图11 选用二次形函数、分段数目为3时网架的最低阶屈曲模态

实际设计中,虽然保证了单根杆件的强度及稳定性,但在网架结构特征值屈曲分析中发现,最低阶屈曲模态出现了杆件的屈曲,说明网架杆件失稳不容忽视。

稳定问题是一个几何非线性的问题,分析过程需要选定较为合适的单元,而选用合适的单元归根结底是选用较为精确的形函数。一般而言,形函数阶次越高,其结果越精确,这也是Beam 188若采用三次形函数,分3段的结果(-1.608 0)已经十分接近精确解(-1.607 5)。若形函数阶次越低,如Beam 188采用一次形函数,分段数目达50时,其结果为-1.609 4,仍与精确解存在误差。

梁单元(Beam 188)中将网架节点处理为刚接,与杆单元(Link 180)虽然有差别,但实际中,网架节点不一定为理想铰接,接近半刚接。考虑到网架结构仅受节点荷载,其受轴力影响较大,采用梁单元分析,对网架的稳定性能影响不大。

3.2 考虑下部框架的网架特征值屈曲分析

网架杆件截面不变,下部框架的混凝土梁柱采用Solid 65单元(加筋混凝土实体单元),考虑钢筋的影响。

3.2.1采用Link 180单元的特征值屈曲分析

采用Link 180单元,通过数值模拟分析得出最低阶屈曲荷载系数为λcr=128.80,其屈曲模态如图12所示。

a—平面图; b—侧视图。

3.2.2用Beam 188单元的特征值屈曲分析

由表7、图13～图16可知,考虑下部框架的网架屋盖最低阶屈曲模态和单一网架屋盖的屈曲模态相近,最低阶屈曲荷载系数比不考虑下部框架(表6)的要小2.36%。

表7 考虑下部框架的网架屋盖最低阶屈曲荷载系数

a—平面图; b—侧视图。

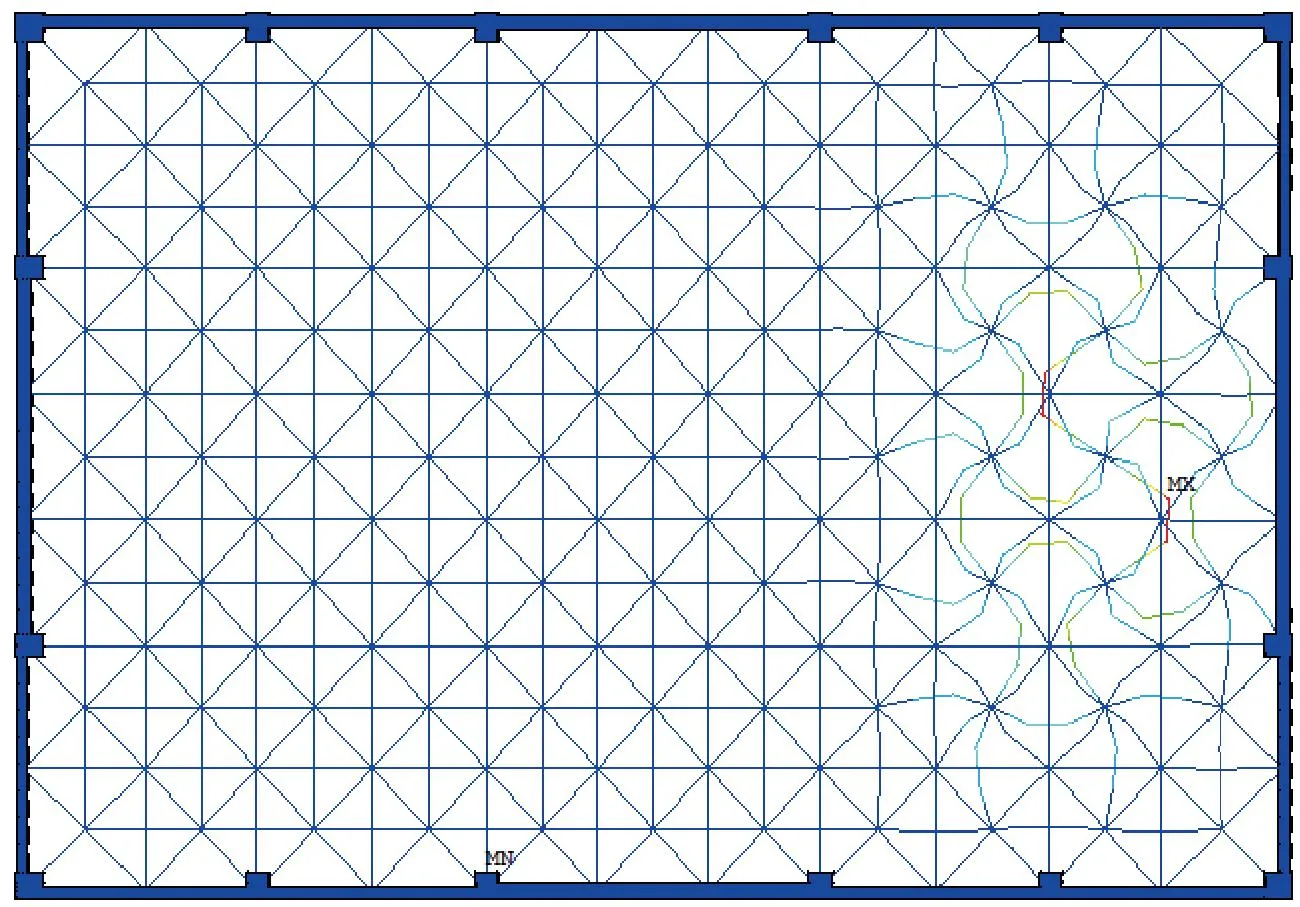
图14 选用一次形函数、分段数目为3时,考虑下部框架的网架最低阶屈曲模态

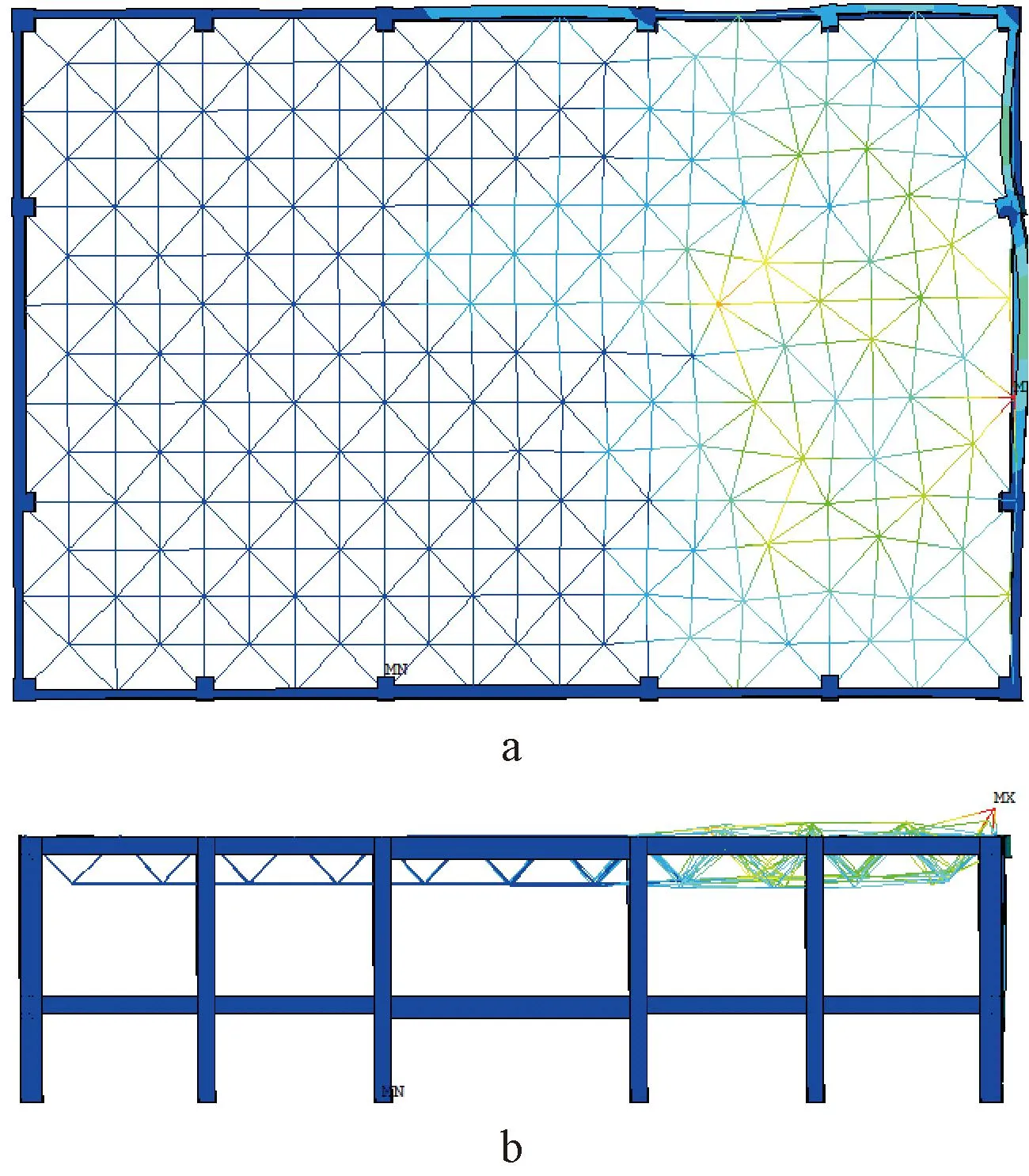
a—平面图(放大2 000倍); b—侧视图(放大2 000倍)。

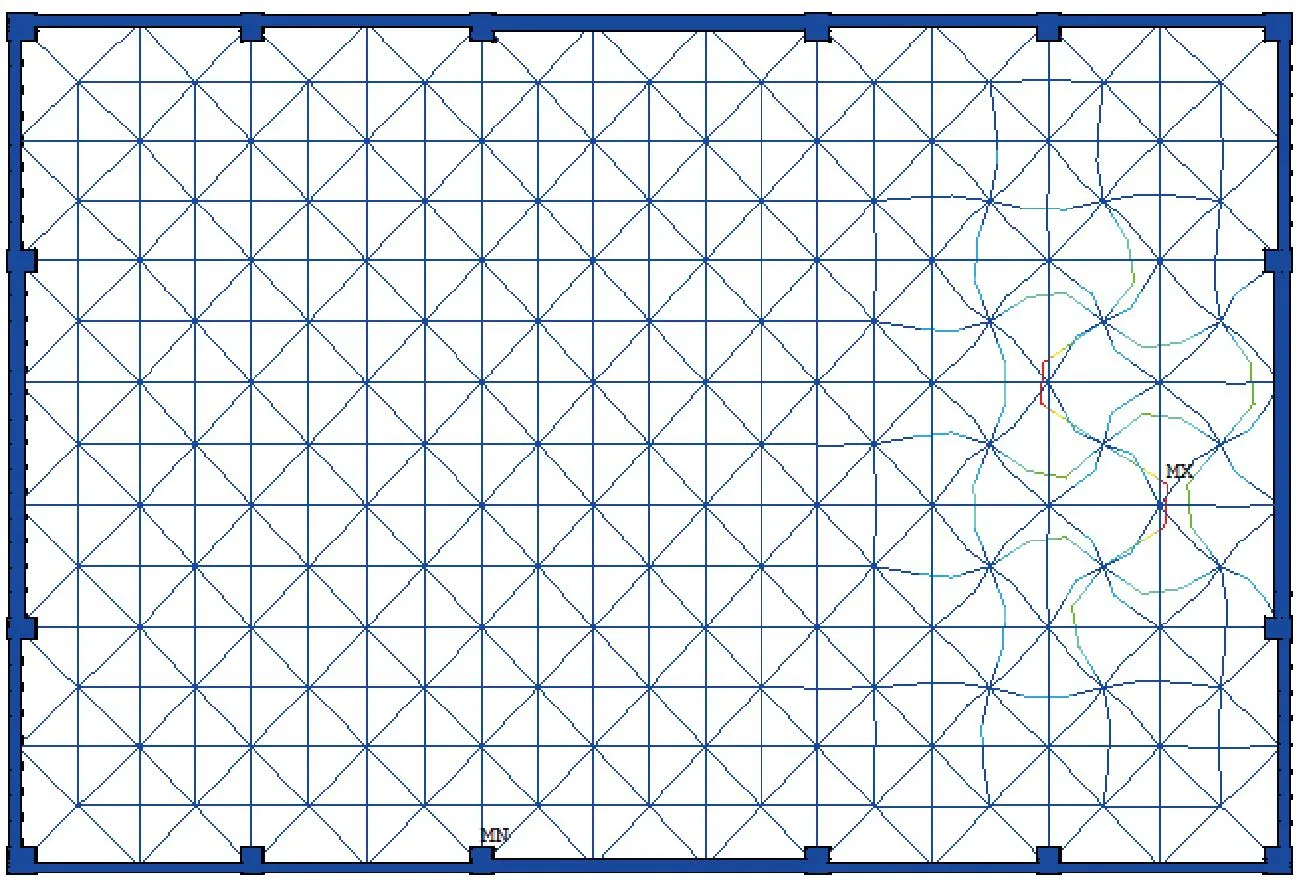
图16 选用二次形函数、分段数目为3时,考虑下部框架网架的最低阶屈曲模态

4 结束语

基于铰支受压杆和铰接桁架稳定性的对比,分别采用杆单元、不同形函数的不分段与分段的梁单元对网架结构工程实例进行特征值屈曲分析,讨论了网架结构特征值屈曲分析中的单元采用多段梁单元的合理性及内在机理,得到以下结论:

1)采用杆单元对网架结构进行特征值屈曲分析时,由于杆单元无法考虑杆件屈曲,使得最低阶屈曲荷载系数过大,会高估网架的整体稳定性。

2)采用梁单元对网架结构进行特征值屈曲分析时,若不分段,无法考虑杆件的屈曲,其形函数阶次越低,求得的最低阶屈曲系数误差越大;采用二阶和三阶形函数的多段梁单元时,网架结构的最低阶屈曲模态中出现杆件失稳。

3)对网架结构特征值屈曲分析时,建议采用多段梁单元对网架进行特征值屈曲分析,以此可以得出较为准确可靠的网架屈曲荷载和屈曲模态。