一种输入电流连续的高电压增益改进型Cuk 变换器*
岳 舟 刘小荻 姚绍华 杨佳霖
(湖南人文科技学院能源与机电工程学院 娄底 417000)
1 引言
由于能源管理的原因,化石燃料的减少以及对环境污染的要求,寻找替代能源成为研究人员面临的一个挑战性问题。近年来,DC-DC 变换器在工业中得到了广泛的应用,随着可再生能源应用的扩大,DC-DC 变换器在工业中占有特殊的地位。在电子产品、燃料电池系统、蓄电池供电系统、便携式设备和电动汽车等诸多应用中都需要具有升降压功能的DC-DC 变换器。因此,需要具有高电压增益、低成本及紧凑型的变换器。光伏系统和燃料电池等能源的输出电压较低,需要高电压增益变换器来调节其输出电压。图1 为光伏发电在直流微电网中应用的系统框图。图1 中主直流母线的规格为400 V,而光伏发电的输出电压一般在12~48 V,所以高电压增益和高效率的变换器是连接光伏板和直流母线以达到所需电压水平的基本要求。
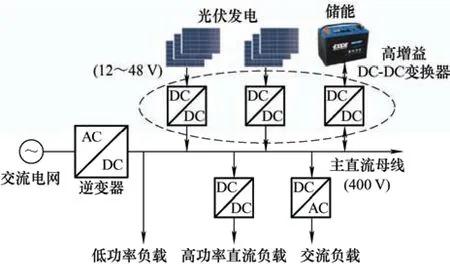
图1 光伏发电在直流微电网中应用的系统框图
高增益DC-DC 变换器分为隔离和非隔离两种[1-3]。其中一种获得高电压增益的方法是使用隔离变换器,通常是利用耦合电感或变压器来实现高电压增益。但这类变换器在带来高电压增益的同时,也有诸如变压器的结构庞大、半导体器件的高电压应力以及高成本等缺点。考虑到这些缺点,隔离变换器不太适用于光伏发电系统或燃料电池的应用。另一种方法是使用非隔离拓扑结构以实现高电压增益。非隔离拓扑通常具有结构简单、重量轻、制造成本低等优点,是一种适合于高电压增益应用的解决方案。在非隔离变换器中,Buck-Boost 变换器结合了Buck 和Boost 变换器的功能[4-5]。
传统的Buck-Boost变换器是最简单的升降压变换器。除此之外,还有Cuk、Zeta、Sepic 等变换器。在这些变换器中,Cuk 变换器因其输入输出电流连续以及负的输出电压等特性,尤其是具有负的输出电压,使其能够直接用于需要负电压源的应用场合,如音频放大器、信号发生器和数据传输接口等[6-7]。
文献[8]提出了一种新的升降压变换器结构,虽然减少了导电元件,但是有两个功率开关,这增加了功率损耗,与传统的升降压变换器相比,电压增益没有改善。文献[9]提出了一种基于Sepic 变换器的无变压器升降压变换器,该变换器中使用了一个主功率开关,但存储元件数量较多。文献[10]介绍了一种基于Zeta 的非隔离变换器,其结构简单成本低,但输入电流不连续。文献[11]提出了一种基于Cuk 的升降压变换器,电压增益高,但连续导通模式(Continuous conduction mode,CCM)下的工作模式与所提变换器不同。文献[12]中提出的升降压变换器由单功率开关组成,但输入电流不连续,电压纹波较大。文献[13]提出了一种多电平Cuk 变换器。该变换器的电压增益适用于光伏应用,但元件数量多,实现困难。文献[14]介绍了一种改进的Cuk 变换器,有两个功率开关,因此功率损耗很高。文献[15]介绍了另一种改进的单功率开关Cuk 变换器。该变换器电压增益高,但储能元件数量多,成本高。
本文提出一种非隔离高电压增益改进型Cuk 变换器。该变换器具有较高的电压增益,高于传统的升降压变换器,如Sepic、Zeta 和Cuk。所提变换器输入输出电流连续,电压纹波小。电路拓扑结构简单,只有一个功率开关,因此,该变换器控制简单且成本低。所提改进型Cuk 变换器可以直接用于需要负电压源的应用场合。本文对该变换器进行了数学分析。此外,为了验证该变换器的可行性,利用Matlab 进行了仿真验证。本文详细描述了连续导通模式CCM 下的拓扑结构及其工作模式。对所提变换器进行了稳态分析,对仿真结果进行了说明,以验证理论分析。
2 拓扑结构及工作原理
所提变换器的拓扑结构如图2 所示。该变换器由一个功率开关S,两个二极管D1、D2,四个电容C1、C2、C3、Co,三个电感L1、L2、L3和一个负载电阻R组成。
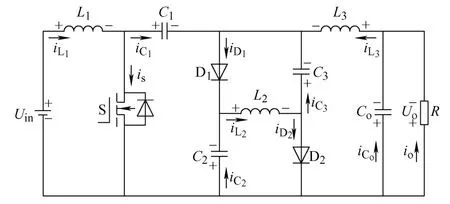
图2 拓扑结构
为了简化变换器的分析,有如下假设:① 功率开关和二极管等所有组件都是理想的;② 电容很大,保持电压恒定。所提变换器在功率开关导通和关断两种状态下,有两种工作模式。CCM 下两种工作模式的等效电路如图3 所示。

图3 等效电路
模式1:在此时间间隔[t0,t1]内,功率开关导通,二极管(D1,D2)关断。如图3a 所示,通过输入电压和由电容磁化的L2和L3来励磁电感L1。电容C1放电,其他电容充电。由此得到以下方程
模式2:在此时间间隔[t1,t2]内,功率开关关断,二极管(D1,D2)导通。如图3b 所示,所有电感均已退磁。电感L1向电容C1提供能量,同时电容C2和C3放电。相关方程如下所示
图4 所示为CCM 下所提拓扑在两种模式下的特征波形。

图4 特征波形
3 稳态分析
3.1 理想电压增益
当所提变换器处于稳态时,在L1和L2上应用伏秒平衡原理,根据式(1)、(2)和式(4)、(5),得到
因为UC2=UC3,代入式(10),得到
根据式(8)和式(11),可以推导出电容C1、C2、C3的电压为
根据式(12)、(13),在L3上应用伏秒平衡原理,所提变换器电压增益的推导计算如下所示
3.2 实际电压增益
为了获得所提变换器的实际电压增益,应考虑寄生值,如二极管和功率开关的导通电阻(rS,rD)、电感和电容(rL,rC)的等效串联电阻(Equivalent series resistance,ESR)以及二极管的正向压降(UFD)。实际电压增益的计算公式如下
3.3 理论计算
根据图3a,在模式1 中
根据图3b,在模式2 中
在电容C2和C3上应用安秒平衡原理
通过简化式(21),得到以下方程
如图3 所示,iin=iL1,式(22)和式(24)可以变换为
将式(25)代入式(26),可以得到电感L2的平均电流
将式(27)代入式(26),可以得到电感L3的平均电流
类似地,将式(27)、(28)代入式(24),可以得到电感L1的平均电流
根据电压增益计算式(16),可以得到输出平均电流
iL3的平均值为
2.1.1 心包完整的钝性暴力致心脏破裂 男性10名,女性1名;年龄38.6±12.8岁;心脏质量304.6±70.6 g,明显小于急性心梗致心脏破裂和主动脉夹层破裂心包填塞组(P<0.05);心包积血量183.0±112.8 mL,明显低于急性心梗致心脏破裂(P<0.05)和主动脉夹层破裂心包填塞组(P<0.01),其中2例高坠致心脏破裂无凝血块,心包积液量分别为3 mL和5 mL,伴有多处的重度损伤(表1,表2,图1)。
根据式(28)和式(32),输入平均电流为
将式(33)代入式(27),得到
功率开关和二极管的电流应力为
在选择合适元器件时,各种电路元件上的电压应力是最重要的因素。功率开关及二极管的电压应力如下
从式(41)、(42)可以看出,通过功率开关及二极管的电压应力较低,且都小于输出电压。
3.4 参数设计
理论分析表明,该变换器工作在CCM 模式下。为了验证所提变换器的最佳性能,并避免高功率损耗和低寿命,电路设计中电感电流的最小值为IL1=ΔiL1/2、IL2= ΔiL2/2和IL3=ΔiL3/2[15]。
考虑上述关系,并根据式(32)~(34)和式(16),设计的电感L1、L2和L3如下所示
电容C1、C2、C3和Co之间的电压波动定义为ΔUC1、ΔUC2、ΔUC3和ΔUCo。选择电容最小值,假设允许的电压纹波为1%。根据输出电流,变换式(32)~(34),则可以根据输出电流获得电容电流。
根据上述方程,设计的电容值如下
3.5 对比分析
与传统的Cuk、Zeta、Sepic 以及Buck-Boost变换器相比,所提变换器的电压增益是它们的两倍。此外,在占空比低于0.67 的情况下,本文所提变换器的电压增益高于文献[16]提出的二次变换器。应该注意的是,DC-DC变换器中更高的占空比会导致更高的损耗[17]。高电压增益DC-DC变换器的一般缺点是在低压侧输入电流大,特别是在大功率应用中。除此之外,高占空比DC-DC 变换器的实际增益与其理想增益不同。由于等效串联电阻的存在,实际增益要低于理想增益。将所提变换器与其他类似变换器在器件数量以及电压增益方面进行对比,如表1 所示。从表1 可以看出,所提变换器的理想电压增益是传统DC-DC 变换器的两倍。所提变换器、传统DC-DC 变换器以及文献[10-11,16]所提变换器的理想电压增益曲线如图5 所示。从图5 可以明显看出,在占空比低于0.67 的情况下,所提变换器的理想电压增益优于与之对比的其他变换器。

表1 所提变换器与其他类似变换器的比较
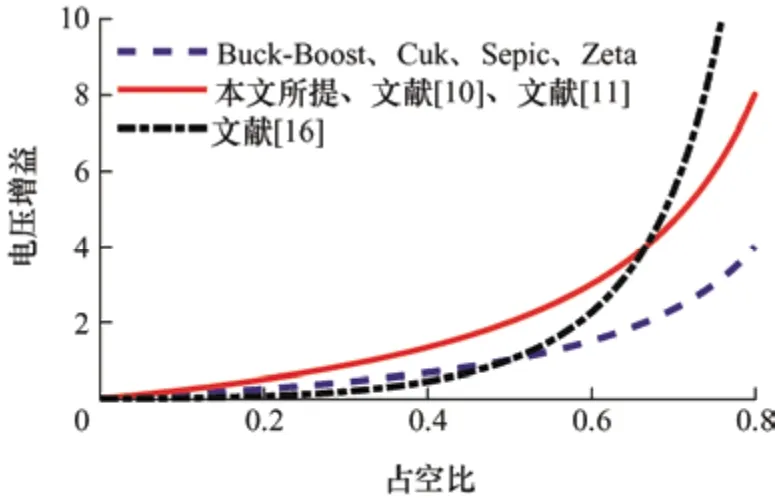
图5 所提变换器与其他变换器的理想电压增益对比
4 仿真结果
为了验证理论分析,采用Matlab 仿真软件进行系统仿真研究,给出了所提变换器在升压和降压模式下的仿真波形。表2 为系统仿真参数。升压模式的波形如图6 所示。如果占空比为60%,则输出电压约为73 V,仿真波形如图6a 所示。略小于理想情况下的75 V 理论值,与理论分析一致。图6b 所示为电感L1、L2和L3的电流波形。如式(32)~(34)所述,L1、L2和L3的电感电流平均值分别为7.2 A、2.4 A 和2.4 A,仿真结果与理论值非常接近。输入电流等于电感L1电流,从仿真结果可以看出其纹波较低。图6c 所示为电感L1、L2和L3的电压波形,电感电压基本一致。图6d 所示为电容C1、C2和C3的电压波形。C2的电压与C3的电压相同。图6e 所示为二极管D1、D2的电流波形。这两个二极管具有相同的电流。当功率开关处于断开状态时,二极管导通。功率开关S 的电流波形如图6f 所示。
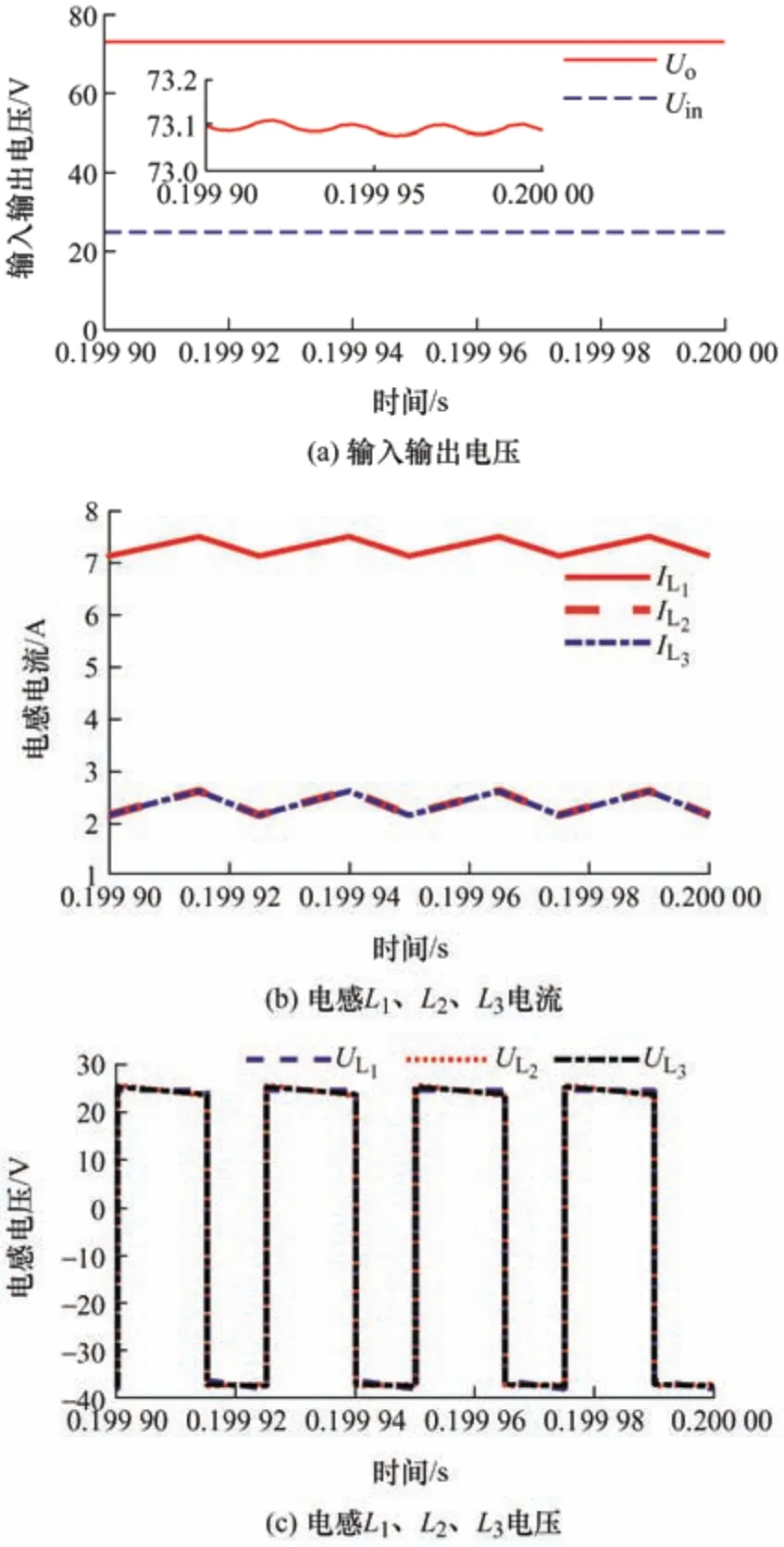

表2 仿真参数

图6 升压模式下仿真波形
降压模式的仿真波形如图7 所示。当占空比为25%时,输出电压约为15 V,如图7a 所示。该实际输出电压值同样小于理论值16.67 V。图7b 所示为电感L1、L2和L3的电流波形。根据式(32)~(34),电感L1、L2和L3的电流平均值分别为0.35 A、0.53 A 和0.53 A。从图7b 可以看出,仿真结果与理论值非常接近。图7c 所示为电感L1、L2和L3的电压波形,电感电压基本一致。图7d 所示为电容C1、C2和C3的电压波形,C2的电压与C3的电压相同。图7e 所示为二极管D1、D2的电流波形。这两个二极管具有相同的电流。当功率开关处于断开状态时,二极管导通。功率开关S 的电流波形如图7f 所示。
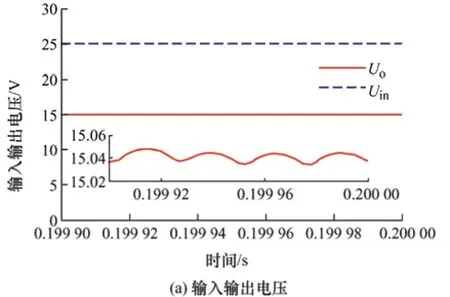
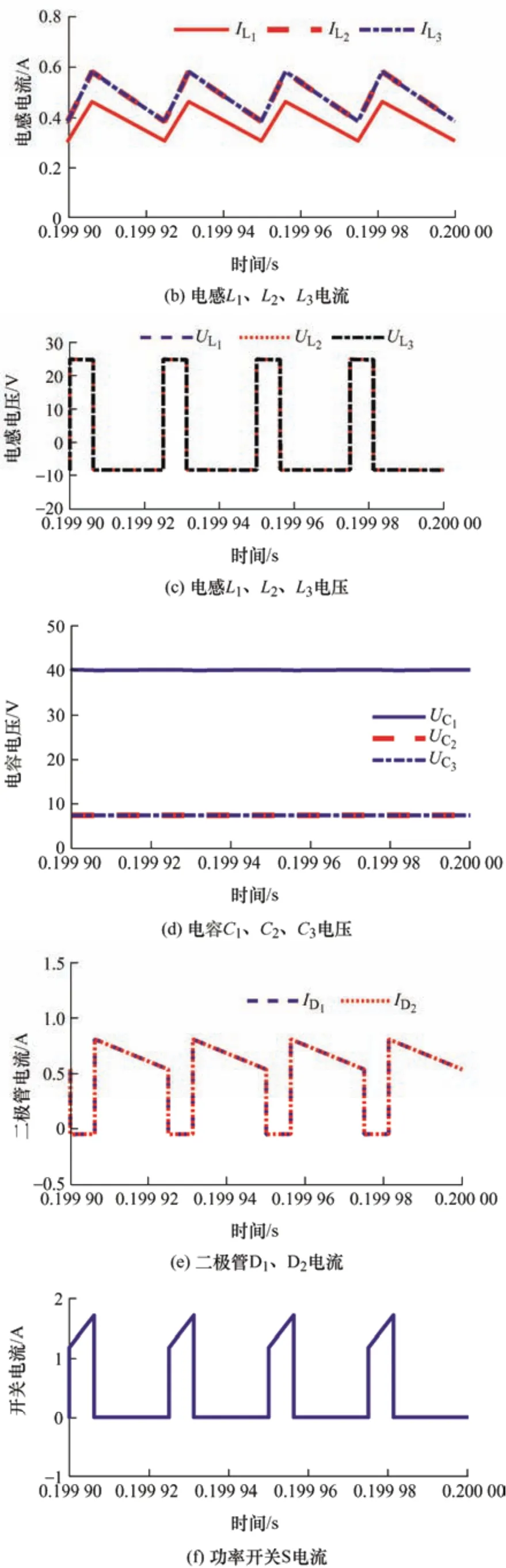
图7 降压模式下仿真波形
本节进一步分析了所提变换器在不同占空比情况下的转换效率。转换效率与占空比的关系曲线如图8 所示。从图8 可以看出,当占空比在0.3~0.6之间系统转换效率在90%以上,系统的最高转换效率约为94%。
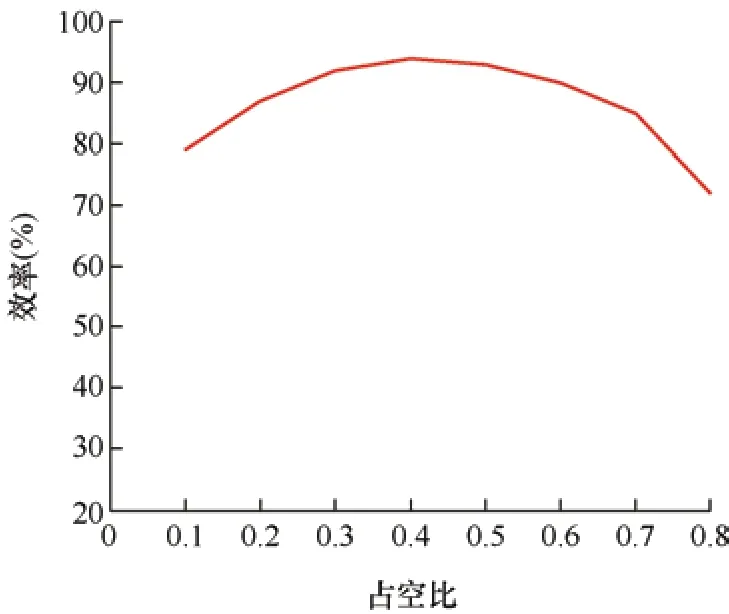
图8 转换效率与占空比的关系曲线
5 样机试验
为进一步验证理论分析的正确性,制作了试验样机。样机中采用的功率开关 S 为 MOSFET(IRFP260N),二极管为DSEP8-06As。功率开关S由TLP350 型IC 驱动[17]。其他电路参数如表2 所示。由于集成电路TLP350 和TLP250 的功能相似,因此详细的驱动电路可参考文献[18]。试验中使用2231-30-3 型 KEITHLEY 电源作为输入源,THDP0200 型差动探头和TPP0250 型探头用于测量电压信息,采用TCP0030A型电流探头测量电流信息[19-20]。所有试验波形均由Te ktronixMDO3024型示波器记录。
在占空比为0.6、纯电阻负载为31 Ω 的升压模式下,运行变换器的试验结果如图9 所示。图9a为输出电压,约为72.77 V,与仿真结果十分接近。图9b 为电容C1和C2的电压,分别约为95.87 V 和35.55 V。功率开关的漏源极电压约为112 V。从试验结果可以看出,图9a 中电感L1的电流波形和图9b 中电感L3的电流波形是连续的,这表明所提变换器具有连续的输入电流和输出电流。因此,试验结果与理论分析非常吻合。类似地,图10 是在占空比为0.25、纯电阻负载为31 Ω 的变换器降压模式下获得的试验结果。试验波形与理论分析结果基本一致,验证了所提改进型Cuk 变换器的特性。
6 结论
本文提出一种非隔离高电压增益改进型Cuk 变换器。所提变换器的电压增益高于传统的Buck-Boost、Zeta、Sepic 和Cuk 变换器。该电路中的功率开关和其他功率元件间具有相对较低的电压应力。所提新型拓扑的主要特点如下所述。
(1) 与传统的DC-DC 变换器相比,提高了电压增益。
(2) 输入电流连续,纹波小,降低了输入滤波器的成本。
(3) 输出电流连续,降低了负载端电容上的电流应力。
(4) 输出电压纹波较小。
由于该变换器具有上述优点,因此适用于光伏应用等领域。

