Mathematica软件在大学物理实验中的应用

徐兵 张建建 许会芳 刘晓伟 孙文洋

摘 要：Mathematica软件在一些需要完成数据处理和仿真模拟等任务的理工科专业课程中被广泛应用。在大学一年级的大学物理实验教学中引导学生使用Mathematica软件进行简单的数据处理和仿真模拟，不仅有利于加深学生对物理知识的理解，还可以显著提升他们的计算机应用能力，从而为后续专业课的学习培养编程思维和能力。本文以四个大学物理实验为例，详细介绍了Mathematica软件在大学物理实验中的画图、数据拟合、数值计算和仿真模拟等功能。

关键词：Mathematica软件；大学物理实验；功能示例；物理教学

Mathematica是一款由Wolfram Research公司开发的科学计算软件，它已成为世界上使用最广泛的数学计算软件之一，并在很多前沿行业的科学计算、仿真、建模等工作中发挥着关键作用。

近年来，Mathematica软件已经被应用到大学物理理论课教学过程中［1］。大学物理教师利用Mathematica软件进行仿真模拟演示可以帮助学生建立起清晰直观的物理图像，从而更好地理解所学知识，这将对提高教学效果起到积极的作用。其实，教师在大学物理课程教学中除了利用Mathematica软件进行仿真模拟演示，也可以将其应用到大学物理实验中［24］。在实验教学中，教师可以向学生简要介绍Mathematica软件的使用方法，指导学生使用该软件进行数据处理。这将充分调动学生学习兴趣，提升他们的科学探索能力。此外，对于一些理工科专业，如电子信息工程等，学生在完成大学物理课程学习之后需要学习一些比较复杂的科学计算专业课程或者进行一些仿真模拟实验。如果学生在大学物理实验课程中基本掌握了Mathematica软件的使用方法，学生可以直接使用Mathematica软件完成一些在后续课程中遇到的复杂计算和仿真模拟。

本文将通过举例详细介绍Mathematica软件在大学物理实验中的画图、数据拟合、数值计算和仿真模拟等功能。

1 Mathematica软件在大学物理实验中的功能示例

1.1 画图功能

Mathematica软件有非常强大的画图功能，人们可以根据自身需要直接调用其中的库函数画出精美的图形。在处理实验数据时，经常用到的画图函数包括：可以画出给定的函数曲线的Plot函数，绘制点集的ListPlot函数，以及绘制点集的线条ListLinePlot函数。这里我们以使用ListLinePlot函数处理《霍尔效应法测定螺线管轴向磁感应强度分布》实验中的数据为例［5］，介绍Mathematica画图功能在大学物理实验中的应用。

螺线管是由绕在圆柱面上的导线构成的。如果导线环绕的密度很大，我们可以把螺线管看成是一列共轴的圆形线圈的并排组合。根据理论计算，这种长直螺线管腔中部的磁场是均匀的，而在靠近两端口处会呈现明显的不均匀性。在实验中，我们在设定霍尔电流IH=5.00mA和线圈的励磁电流IM=500mA后，将霍尔器件从螺线管的一端（x=0cm）逐渐移到另一端（x=30cm），并运用对称测量法依次得到在不同位置处的霍尔电压UH。最后，根据计算公式B=UHKHIH，我们得到了螺线管在轴线上特定点处的磁感应强度，如表1所列。

我们以x为横轴，磁感应强度B为纵轴，利用Mathamatica列出表1中数据并将其连接成曲线。用到的程序命令如下：

In［1］：=x={0，2，4，6，8，10，12，14，15，16，18，20，22，24，26，28，30}；

B={1.01，4.12，6.51，6.98，7.15，7.19，7.21，7.22，722，7.22，7.21，7.18，7.16，6.97，6.42，3.98，0.99}；

In［3］：=Data=Table［{x［［i］］，B［［i］］}，{i，1，Length［x］}］；

In［5］：=ListLinePlot［Data，Mesh→Full，Frame→True，FrameLabel→{"X（cm）"，"B（mT）"}，PlotRange→{0.5，75}，PlotTheme→"Detailed"］

上述程序中In［i］：=表示第i個输入命令。运行该程序，我们可以得到长直螺线管的轴向磁场分布，如图1所示。

图1 螺线管轴向磁感应强度分布曲线

1.2 数据拟合功能

学生在处理物理实验数据时会遇到从测量数据拟合出特定函数形式的情况，例如《光电效应法测量普朗克常量》和《偏振光的观测与应用》等。这时，学生可以使用Mathematica软件中的功能丰富的Fit、FindFit和FittedModel等命令完成数据拟合。

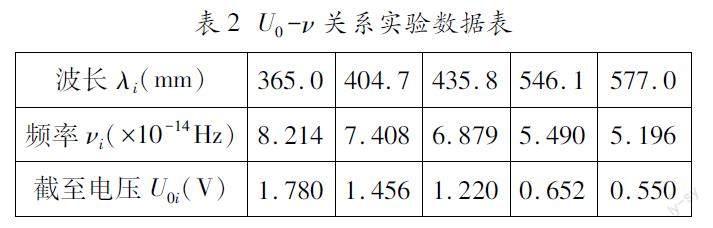
本文，我们以《光电效应法测量普朗克常量》实验为例介绍Fit命令的使用方法。该实验中，在利用光电效应试验仪测得如表2中所示的五组不同入射光（波长分别为λi）对应的截止电压U0i后，我们需要利用一次函数U0=he（ν-ν0）推导出普朗克常量h。具体地讲，使用五组U0i-νi数据拟合出U0-ν之间满足的一次性函数关系及其斜率k并由h=k×e计算出普朗克常量h。

Mathamatica程序如下：

In［1］：=λi={365.0，404.7，435.8，546.1，577.0}；

In［2］：=U0i={1.780，1.456，1.220，0.652，0.550}；

In［3］：=νi=（2.99792458*108）/（λi*10-9）

Out［3］：={8.213492×1014，7.407770150728935×1014，6.879129371271225×1014，5.489698919611792×1014，5195709844020797×1014}

In［4］：=data=Table［{νi［［j］］，U0i［［j］］}，{j，1，Length［λi］}］；

In［5］：Fit［data，{1，ν}，{ν}］

Out［5］：-1.59386+4.10637×10-15ν

In［6］：h=4.10637*10-15*1.602*10-19

Out［6］：6.5784*10-34

In［7］：Abs［（%-6.626*10-34）/（6.626*10-34）］

Out［7］：0.00718311

上述程序中Out［i］：=表示第i個输入命令运行后的输出结果。通过运行该程序，我们可以直接得到不同波长入射光的频率（如Out［3］所示）以及通过拟合测量数据得到的U0-ν一次函数关系（如Out［5］所示）。最后通过计算得到普朗克常量h的测量值（如Out［6］所示）及其相对误差（如Out［7］所示）。

1.3 数值计算功能

Mathematica软件的数值计算能力十分强大，它内嵌几千个函数，可以满足多学科中对大规模复杂计算的需求。我们可以使用Mathematica软件完成数据量繁杂的实验数据处理。本文以《光的等厚干涉现象与应用——牛顿环的测定》为例介绍Mathematica在处理大量实验数据处理和数值计算方面的应用。

在该实验中，我们将通过测量牛顿环计算出平凸透镜的曲率半径R。通过调节牛顿环仪观测到清晰的牛顿环图像后，我们将十字叉丝水平线的方向与读数显微镜移动方向平行并旋转读数轮获得第m暗环对应的位置。表3汇总了利用波长λ=589.3nm的单色光进行实验获得的观测数据。

利用表3中的测量数据我们可以计算出第m环的直径dm，然后利用计算公式：R=dm2-dn24（m-n）λ得到五组R的测量值，最后我们对其取平均得到平凸透镜的曲率半径R的最终测量结果。在此过程中，由于数据量较大，计算过程也比较多，我们可以使用Mathematica程序进行数据的处理并得到最终的计算结果。详细的程序如下：

In［1］：=DataLm1={21.859，21.797，21.738，21.668，21.585}；

DataRm1={14.382，14.473，14.555，14.608，14.689}；

In［3］：=DataLm2={14.380，14.453，14.528，14.609，14.679}；

DataRm2={21.856，21.789，21.722，21.648，21.580}；

In［5］：=DataLn1={21.102，21.012，20.918，20.815，20.718}；

DataRn1={15.175，15.286，15.351，15.459，15.547}；

In［7］：=DataLn2={15.151，15.243，15.331，15.420，15.523}；

DataRn2={21.082，21.002，20.910，20.815，20.712}；

In［9］：=dm=（Abs［DataLm1-DataRm1］+Abs［DataLm2-DataRm2］）/2；

In［10］：=dn=（Abs［DataLn1-DataRn1］+Abs［DataLn2-DataRn2］）/2；

In［11］：=Ri=（dm2-dn2）/（4*10*589.3*106）；

In［12］：=MR=Mean［Ri］

Out［12］：=879.604

通过运行上述程序，我们可以很快得到本次实验我们测得的平凸透镜的曲率半径R=879.604mm。

1.4 仿真模拟功能

在《示波器的使用》实验中，学生需要学会用示波器观察“拍”效应波形和李萨如图形。为了让学生更加清晰地理解波形的产生原理，我们可以使用Mathematica软件实现简谐振动合成的仿真模拟。这里我们以两个相互垂直的简谐振荡的合成为例，介绍李萨如图形的产生过程。以下是Mathematica程序命令：

In［1］：=Manipulate［ParametricPlot［{A1Cos［ω1t+10］，A2Cos［ω2t+20］}，{t，0，20Pi}，

PlotRange→1.05，PerformanceGoal→"Quality"，AxesLabel→{"x/cm"，"y/cm"}］，

Style［"Vertical："，Bold，Medium］，

Dynamic［ParametricPlot［{A1Cos［ω1t+10］，t}，{t，0，2 Pi}，ImageSize→100，AspectRatio→1，PlotRange→{{-1，1}，{0，2 Pi}}］］，{{ω1，2，"Frequency ω1"}，1，4}，{{A1，1，"Amplitude A1"}，0，1}，{{10，0，"Phase 10"}，0，2 Pi}，

Delimiter，Style［"Horizontal："，Bold，Medium］，

Dynamic［Plot［A2Cos［ω2t +20］，{t，0，2 Pi}，ImageSize→100，AspectRatio→1，PlotRange→1］］，{{ω2，3，"Frequency ω2"}，1，4}，{{A2，1，"Amplitude A2"}，0，1}，{{20，Pi/4，"Phase 20"}，0，2 Pi}，ControlPlacement →Left］

通过运行上述Mathematica程序命令，我们可以得到两个简谐振动x=A1cos（ω1t+φ10）和y=A2cos（ω2t+φ20）在设置为振幅相等、频率比为2∶3、初始相位差为π/4时合振动的轨迹，如图2所示。同时，我们可以改变两个简谐振动的振幅、频率和初始相位得到更多形式的李萨如图形。

2 结论

基于Mathematica在数值计算、绘图和动画显示等方面的强大能力，我们可以使用Mathematica完成大学物理实验中的数据处理和仿真模拟等实验过程。这样，在辅助完成实验任务的同时，将加深学生对物理知识的理解，提高他们的科学素养，激发他们的学习兴趣。此外，对于一些对计算机使用要求比较高的专业学生而言，在大学物理实验中使用Mathematica软件辅助完成实验，从大一年级开始锻炼他们应用计算机的能力，有利于培养他们的编程思维和能力，从而为后续的专业课学习打下坚实的基础。因此，作者认为大学物理实验教师应该在教学过程中加强对学生使用Mathematica等计算机软件的示范和引导。

参考文献：

［1］赵近芳.大学物理学［M］.北京：北京邮电大学出版社，2018.

［2］陈学文，张家伟，姚雪，等.基于Mathematica的光的干涉实验的仿真模拟［J］.实验技术与管理，2020，37（09）：165169.

［3］胡宗元.基于Mathematica的大学物理模拟实验［J］.大学物理实验，2015，28（04）：9295.

［4］王高亮，孟明，王强.基于Mathematica的杨氏双缝干涉实验仿真［J］.周口师范学院学报，2018，35（05）：4244.

［5］章毛连.大学物理实验［M］.北京：中国农业出版社，2014.

基金项目：安徽科技学院教育教學改革研究项目（No.X2021036；No.X2021077；No.X2021034）

作者简介：徐兵（1991— ），男，汉族，山东滨州人，博士，讲师，研究方向：引力理论与宇宙学。