不可压缩磁流体方程的全解耦和无条件能量稳定格式
周 帅,陈建华,王 琨,张国栋
(烟台大学数学与信息科学学院,山东 烟台 264005)
磁流体动力学是研究等离子体等导电流体与电磁场的相互作用的物理学分支,在天体物理、热核反应、工业应用[1-3]等众多物理和工程分支中有着广泛的应用。导电流体可以在磁场的作用下产生电流,同时感应电流与磁场相互作用,进而形成洛伦兹力,并能改变流体的行为。因此,磁流体方程(MHD)将不可压缩的纳维-斯托克斯(Navier-Stokes)方程与麦克斯韦(Maxwell)方程耦合起来。近年来有许多关于MHD方程数值方法的研究[4-12]。对于稳态的MHD方程,GUNZBURGER等[13]研究了标准的Galerkin有限元离散。SCHÖTZAU等[14]提出了一种求解非凸多面体MHD方程的混合有限元方法。WACKER等[15]考虑了一种局部投影的方法来稳定线性化MHD方程的两个不足条件。
用数值方法求解非线性耦合的磁流体方程,一个具有挑战性的问题是设计一种解耦线性的算法,同时保持能量稳定性,即能量耗散定律能够保持在离散的水平。全隐格式和耦合的半隐格式是无条件能量稳定的,但是它们在每一个时间层上都需要解决一个耦合系统,这会导致昂贵的时间消耗。所以,解耦是首先要解决的问题,在保持能量稳定的同时也节省了时间成本。对于非定常纳维-斯托克斯方程的求解,投影方法是最流行的解耦方法之一[16-18]。AN等[19]提出了一阶线性耦合的投影方法求解单鞍点型磁流体方程,并证明了该方法的误差估计,由于方程是耦合的,所以在计算过程中时间消耗会比较大。CHOI等[5]发展了两种基于投影方法求解单鞍点型磁流体方程的无条件稳定的耦合格式。文献[20-21]给出了单鞍点型磁流体方程的一阶全离散投影格式的稳定性证明和误差分析。
本文针对双鞍点型磁流体方程提出了一个线性的、无条件能量稳定的、全解耦格式。对于模型的耦合困难,采用投影方法将压力与速度解耦和拉格朗日乘子与磁场解耦,并且引入一个一阶精度的稳定项来稳定磁场和速度场的解耦计算。对于模型的非线性困难,采用隐式-显式方法来处理非线性项,并且在非线性项的线性化处理中保持反对称结构。
1 磁流体方程和能量定律
设Ω是d(d=2,3)中的有界且单连通区域,考虑下面的磁流体方程:

(1)
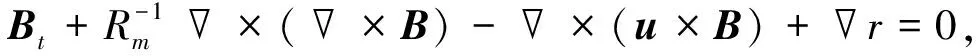
(2)
·u=0,
(3)
·B=0,
(4)
u|∂Ω=0,B×n|∂Ω=0,r|∂Ω=0,
(5)
u|t=0=u0(x),B|t=0=B0(x)。
(6)
其中,(x,t)∈Ω×(0,T],u为速度场,p为压力场,B为磁场,r为拉格朗日乘子,物理参数Re,Rm和s分别为流体雷诺数、磁雷诺数和耦合系数,n表示∂Ω的单位外法向。
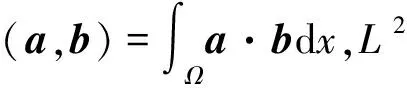
H(curl,Ω)={ω∈L2(Ω)d:×ω∈L2(Ω)d},

注1r是与约束·B=0相关的拉格朗日乘子,对式(2)取散度,得到·Bt+Δr=0,由于得到r≡0。
系统(1)~(6)遵循能量耗散定律:令式(1)与u作L2内积,式(2)与sB作L2内积,利用式(3)~(4)和分部积分公式,得到
对这两个等式求和得

2 时间半离散格式
本节提出时间半离散格式,并证明其无条件能量稳定性。对系统(1)~(6)构造如下格式,给定(un,Bn,pn,rn),通过以下步骤计算(un+1,Bn+1,pn+1,rn+1):

(7)


(8)
求解un+1和pn+1满足:

(9)
·un+1=0,
(10)
un+1·n|∂Ω=0,
(11)
求解Bn+1和rn+1满足:

(12)
·Bn+1=0,
(13)
rn+1|∂Ω=0。
(14)


将上述三个式子联立可以得到数值格式中的式(7)、(8)。
注2对式(9)取散度,可得pn+1满足
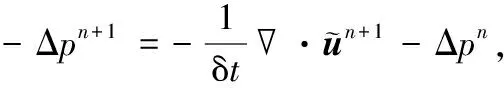
(15)

(16)
注3对式(12)取散度,可得rn+1满足

(17)
利用边界条件rn+1|∂Ω=0求解rn+1。然后计算Bn+1满足

(18)
下面证明格式(7)~(14)的稳定性。
定理1格式(7)~(14)具有如下能量稳定性:
‖un+1‖2+s‖Bn+1‖2+ δt2‖pn+1‖2+sδt2‖rn+1‖2+
‖un‖2+s‖Bn‖2+ δt2‖pn‖2+sδt2‖rn‖2。
(19)

(20)
这里用到了分部积分
和

(21)
这里用到了
格式中(u·)u保持了反对称结构,因此取检验函数并与之做内积,并利用((u·)v,v)=0的结论可以在稳定性分析中将此非线性项消去,从而能够简化证明过程。
接下来,将式(9)重写为
等式两边与自身做内积,得

(22)
同理可得

(23)
将式(20)和(21)组合,利用式(22)和(23)得到
‖un+1‖2-‖un‖2+s‖Bn+1‖2-s‖Bn‖2+δt2‖pn+1‖2-δt2‖pn‖2+

(24)
其中
(25)
把式(25)代入式(24),可得式(19)。
3 全离散格式

定义协调有限元空间为
Ch:={B∈H0(curl,Ω):B|K∈Nk(K),K∈Th},
此外,有限元空间Xh和Mh必须满足inf-sup条件
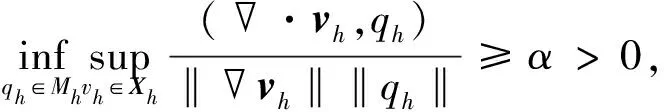
(26)
其中常数α与h无关。由于Sh⊂Ch,有限元空间Ch和Sh自然满足inf-sup条件
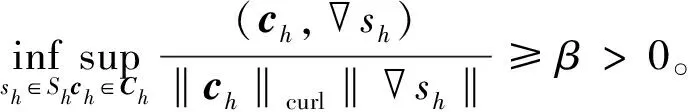
(27)
基于格式(7)~(14)的全离散有限元格式如下:

(28)
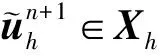

(29)


(30)


(31)

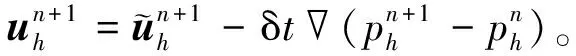
(32)
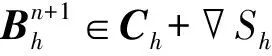
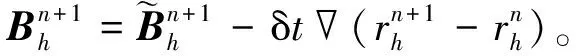
(33)
注4对于式(29)中的对流项,使用以下三线性形式:

因此可得
b(u,v,v)=0,u∈L2(Ω)d,v∈H1(Ω)d。
(34)

上式结合式(30)可得

(35)
同理可得

(36)
可清楚地看到格式(28)~(33)是线性的,全解耦的。
定理2 格式(28)~(33)具有如下的无条件能量稳定性:
(37)

(38)

(39)
(40)
同理可得
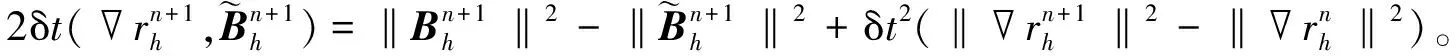
(41)
最后将式(38)~(41)结合,可得
(42)
其中
(43)
将式(43)代入式(42)得
(44)
定理得证。
4 数值实验
在数值实验中,对于速度u,压力p,以及拉格朗日乘子r,使用标准的P1b-P1-P1元,对于磁场B使用最低阶的Nédélec′s元。这里,速度和压力满足inf-sup条件(26),磁场和拉格朗日乘子满足inf-sup条件(27)。
4.1 时间收敛阶测试
使用Ω=[0,1]×[0,1]上的解析解来计算时间收敛阶,选择精确解:
u=(ycos(t),xexp(t)),B=(yexp(t),xcos(t)),p=0,r=0,


表1 解耦格式的误差和收敛阶
4.2 空间收敛阶测试
用Ω=[0,1]×[0,1]上的解析解来计算空间收敛阶,选择精确解:
u=(sin(2πy)sin(πx)sin(πx)exp(t),-sin(2πx)sin(πy)sin(πy)exp(t)),
B=(sin(πx)cos(πy)exp(t),-sin(πy)cos(πx)exp(t)),
p=(2x-1)(2y-1)cos(t),
r=0。
取s=Re=Rm=1,T=1,表2给出了解耦格式中速度的H1误差‖eu‖H1,磁场的L2、H(curl)误差(‖eb‖L2,‖eb‖curl)和压力的L2误差‖ep‖L2,它们具有一阶精度,速度的L2误差‖eu‖L2具有二阶精度,拉格朗日乘子r接近于0。

表2 解耦格式当δ t=h时的误差和收敛阶
同理,在Ω=[0,1]×[0,1]上使用相同的解析解来计算已有的耦合算法,方程如下:
取s=Re=Rm=1,T=1,表3给出了耦合算法中速度的H1误差‖eu‖H1,磁场的L2、H(curl)误差(‖eb‖L2,‖eb‖curl)和压力的L2误差‖ep‖L2,它们具有一阶精度,速度的L2误差‖eu‖L2具有二阶精度,拉格朗日乘子r接近于0。

表3 耦合算法当δ t=h时的误差和收敛阶
表2与表3相比较能够得出本文提出的全解耦算法与已有的耦合算法在精度上大致相同,但在运行速度方面,全解耦算法要比已有的耦合算法运行速度快,所用的时间相对较短。
4.3 稳定性测试

u0=(x2(x-1)2y(y-1)(2y-1),-y2(y-1)2x(x-1)(2x-1)),
B0=(sin(πx)cos(πy),-sin(πy)cos(πx)),
p0=0,
r0=0。

图1 解耦格式的能量曲线
4.4 Hartmann流
Hartmann流描述了不可压缩粘性导电流体在外部磁场Bd作用下沿均匀矩形截面管道的流动。考虑边界条件
u=0,y=±1,
B×n=Bd×n, ∂Ω。
该模型具有精确解

取Lx=4和G=1,考虑以下四种情形:
Ha=0.1,Re=Rm=0.1,s=1;
Ha=1.0,Re=Rm=1.0,s=1;
Ha=10,Re=Rm=10,s=1;
Ha=90,Re=Rm=30,s=9。
图2和图3分别给出了该格式在δt=1/100,h=1/128四种情形下的数值解u1和B1,可以发现它们与精确解很好地吻合。
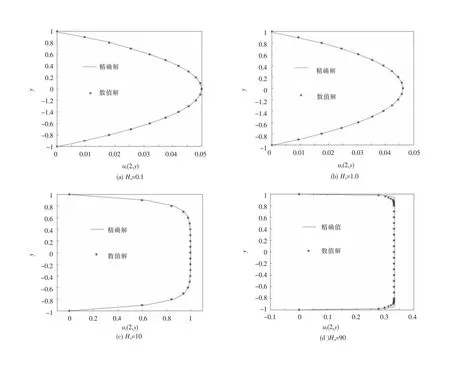
图2 数值解u1与精确解

图3 数值解B1与精确解
5 结束语
对双鞍点型磁流体方程提出了一个全解耦的线性高效格式,并严格证明了它的无条件稳定性。该格式的主要特点是将耦合的非线性双鞍点磁流体系统转化为几个线性椭圆问题,并在非线性项的线性化过程中保持了反对称结构。通过一系列的数值模拟,包括收敛性试验、能量稳定性试验和Hartmann流试验,验证了格式的稳定性和收敛性。该格式的误差估计将是后续工作的主要目标。

