Comprehensive modeling of frictional pressure drop during carbon dioxide two-phase flow inside channels using intelligent andconventional methods

Mohammad Amin Moradkhani, Seyyed Hossein Hosseini,, Mengjie Song

1 Department of Chemical Engineering, Ilam University, 69315-516 Ilam, Iran

2 Department of Energy and Power Engineering, School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

Keywords: CO2 Two-phase flow Frictional pressure drop Intelligent approaches Correlation

ABSTRACT Environmentally friendly nature of CO2, associated with its safety and high efficiency, has made it a widely used working fluid in heat exchangers. Since CO2 has strange thermophysical features, specific models are required to estimate its two-phase characteristics, particularly frictional pressure drop(FPD). Herein, a widespread dataset, comprising 1195 experimental samples for two-phase FPD of CO2 was adopted from 10 sources to fulfill this requirement. The literature correlations failed to provide satisfactory precisions and exhibited the average absolute relative errors (AAREs) between 29.29% and 67.69% from the analyzed data. By inspiring the theoretical method of Lockhart and Martinelli, three intelligent FPD models were presented, among which the Gaussian process regression approach surpassed the others with AARE and R2 values of 5.48% and 98.80%, respectively in the test stage. A novel simple correlation was also derived based on the least square fitting method, which yielded opportune predictions with AARE of 19.76%for all data.The truthfulness of the newly proposed models was assessed through a variety of statistical and visual analyses, and the results affirmed their high reliability over a broad range of conditions, channel sizes and flow patterns. Furthermore, the novel models performed favorably in describing the physical attitudes corresponding to two-phase FPD of CO2. Eventually, the importance of operating factors in controlling the FPD was discussed through a sensitivity analysis.

1. Introduction

During the last decades, by growing the concerns regarding environmental issues, the use of hydrochlorofluorocarbons (HCFs)and chlorofluorocarbons(CFCs)as working fluids in heat exchangers have been limited due to their harmful influences on ozone layer and global warming[1].In order to protect the environment,trends toward the natural refrigerants have been enhanced, since they have negligible values of ozone depletion potential (ODP)and global warming potential (GWP). Nevertheless, some of natural refrigerants suffer from several drawbacks such as flammability and toxicity, which may restrict their applications in industries.CO2is recognized as a safe(non-toxic and non-flammable)natural refrigerant associate with environmentally friendly characteristics(GWP of one and ODP of zero) [2–4]. On the other hand, it has shown comparable performances with all conventional refrigerants in air conditioners of automobiles,refrigeration systems,heat pumps,etc.[5–13].

Compared to other working fluids, CO2has considerably lower vapor viscosity and surface tension,and higher thermal conductivity, heat capacity and vapor density [14]. With such unique properties, CO2has radically different thermal and hydrodynamic properties than conventional refrigerants [15–18]. This is why the models developed based on data corresponding to other fluids are unable to properly describe the heat transfer coefficient (HTC)and frictional pressure drop (FPD) of CO2during two-phase flow inside tubes.Several models are available in the literature for predicting the two-phase HTC of CO2in various systems [19–22].However, in order to efficiently design the heat exchangers with CO2as refrigerant, it is also vital to have knowledge about the two-phase FPD.

The two-phase FPD of CO2has been experimentally investigated in various studies [23–27]. Adamset al. [28] studied the influence of mass flux on the FPD of CO2in a 14-port mini channel with an inner diameter of 1.02 mm. It was found that the FPD is dramatically increased by enhancing the total mass flux. Also, comparing the performances of R245fa with those of CO2revealed that the latter leads to extremely lower FPD under a similar situation.Cho and Kim [29] reported experimental data for FPD of CO2in conventional channels with outer dimeters of 5 and 9.52 mm.The results indicated that increasing the total mass flux,and declining the saturation temperature and channel diameter result in higher twophase FPD. In another work, Park and Hrnjak [30] evaluated the two-phase FPD of CO2inside a tube with 6.1 mm inner diameter,and compared the corresponding results with those of R410A and R22. The results obtained acknowledged that the two-phase FPD values when using the CO2as working fluid is much lower than those when using the conventional refrigerants. Heoet al.[31] measured the FPD of CO2during two-phase flow in a minichannel with 1.5 mm inner diameter. It was found that the influence of vapor quality on FPD is obvious at high mass fluxes.In contrast, at low mass flux, the variation of FPD with vapor quality is not noticeable when the flow mass flux is low.In the experimental study carried out by Fronk and Garimella [32], the FPD of CO2in micro-channels with different diameters was investigated.According to the results, the two-phase FPD is remarkably increased by reducing the tube diameter, and this issue was more evident at higher mass fluxes and lower reduced pressures. Recently, Zhanget al. [33] examined the effects of different parameters on FPD of CO2during flow boiling inside mini-channels. While the twophase FPD was highly dependent to saturation temperature and mass flux, the influence of heat flux on FPD was negligible. The same observations were also reported by Wuet al. [34].

The insufficient precision of the available correlations for describing the FPD of CO2during two-phase flow inside channels has been proved in several studies. As mentioned earlier, the primary cause of this issue refers to the strange thermophysical characteristics of CO2. Cho and Kim [29] compared their own experimental data with the predictions of the Chisholm[35]correlation. The results showed that this model is unable to properly estimate the behavior of FPD. Mastrulloet al. [24] provided a review on the performances of the available models to predict the two-phase FPD of CO2based on 125 experimental data. It was found that none of earlier correlations can be considered as an accurate predictive approach,since their total average absolute relative error (AARE) values were higher than 30%. Heoet al. [31]assessed the capabilities of five existing FPD correlations based on measured data. All models exhibited unsatisfactory outcomes with AAREs greater than 29%. In another related work, Kanget al.[27] reported the AAREs higher than 28% between their measured values and those predicted by three general correlations.Fronk and Garimella[32]compared their experimental data for FPD of CO2in micro-channels with eight well known models.The results demonstrated that the available models often under-estimate the FPD,and the best AARE value obtained by these models was 24%.

The above brief review demonstrates the lack of universal and reliable predictive methods verified by a large number of experimental data for FPD during two-phase flow of CO2, as a safe, efficient and environmentally friendly working fluid. In addition, the intelligent approaches have not been applied so far to model this fundamental parameter. On the other hand, having knowledge regarding the most important operating parameters in controlling the FPD of CO2can contribute to efficiently design the heat exchangers with CO2as working fluid. To fulfill these requirements, in the current study, an extended dataset, including 1195 experimental samples was adopted from 10 independent studies,which envelops a wide range of channel sizes, reduced pressures,vapor qualities and flow mass fluxes.Firstly,the exactness of existing correlations is assessed by the experimental data.After detecting the most important input variables through the Spearman’s correlation analysis, the intelligent modeling approaches, including multilayer perceptron (MLP), Gaussian process regression(GPR)and radial basis function(RBF)are implemented to establish new dimensionless predictive methods for FPD of CO2. Furthermore, a novel explicit correlation is also presented employing the conventional technique of least squares fitting method (LSFM).The reliability of the newly proposed models,and their superiority to the literature correlations are evaluated using several statistical and visual analyses. Eventually,a sensitivity analysis is performed to understand the importance of operating parameters in controlling the FPD of CO2.

2. Methodology

2.1. Intelligent approaches

As robust and capable tools to solve the complicated engineering problems, the intelligent methods, such as machine learning algorithms have received much attentions during the last decade[36–43]. In the current study, the intelligent modeling phase was performed by employing the robust approaches of MLP, RBF and GPR. A detailed description regarding the background of these methods have been provided in Supplementary Material.

2.2. Data gathering

Availability of reliable data is of great importance for designing data-driven predictive models [44–47]. In the current study,attempts were made to gather as much data as possible regarding the FPD during two-phase flow of CO2inside channels. Hence, a total number of 1195 measured data extracted from 10 published sources [25–34] were employed in order to develop the novel models. The ranges of operating parameters corresponding to the analyzed sources have been reported in Table S1 Supplementary Material. It is obvious that the collected databank envelops the experimental data for two-phase FPD of CO2over extensive ranges of hydraulic diameters,mass fluxes and reduced pressures.Hence,it can be employed to establish robust and comprehensive predictive models.

2.3. Error analysis

The precisions of the novel and earlier models in predicting the two-phase FPD of CO2were competitively assessed by the statistical parameters,including coefficient of determination(R2,%),standard deviation (SD, %) and average absolute relative error (AARE,%),

whereEidenotes the relative error defined as,

3. Results and Discussion

3.1. Applicability of literature correlations to predict the FPD of CO2

Several correlations are available in the open literature to estimate the two-phase FPD of various fluids inside channels. Among them,the most widely used ones are those presented by Chisholm[35], Friedel [48], Muller-Steinhagen and Heck [49], Koyamaet al.[50], Hosseinet al. [51], Sun and Mishima [52], Zhanget al. [53],Kim and Mudawar [54], Jigeat al. [55], Guet al. [56] and Moradkhaniet al.[57].In order to examine the applicability of these models for predicting the FPD of CO2,their outcomes were compared to the present experimental data, and the corresponding error metrics have been summarized in Table 1.It is clear that all FPD models present fairly large deviations for CO2two-phase flow,and most of data predicted by them have relative errors higher than 20%from the actual values. The Moradkhaniet al. [57] correlation shows the best agreements with the collected data with AARE andR2of 29.29% and 86.02%, respectively. In fact, this correlation is the only predictive method that its AARE value is less than 30%, and predicts most of data in ±30% error bounds. The models proposed by Jigeat al. [55], Muller-Steinhagen and Heck [49],Kim and Mudawar [54], Friedel [48] and Sun and Mishima [52]exhibit the AAREs between 35.45% to 39.39%, and ranks second to sixth in term of exactness.It should be noted that most of values calculated by these models have relative errors larger than 30%,and they cannot be considered as reliable approaches for estimating the two-phase FPD of CO2. The remaining five models provide poor estimations with AAREs exceeding 40%. Fig. S4 depicts the values of two-phase FPD of CO2calculated by the most accurate literature correlations against the measured data. As observed, the results of Moradkhaniet al.[57]correlation are closer to the actual values compared to the other models. However, there are a lot of data beyond the±30%error bounds for all models,which confirms the fact that the two-phase FPD of CO2is entirely different from the other working fluids due to its strange thermophysical characteristics. Thus, more reliable CO2-specific models should be derived based on the available experimental data.

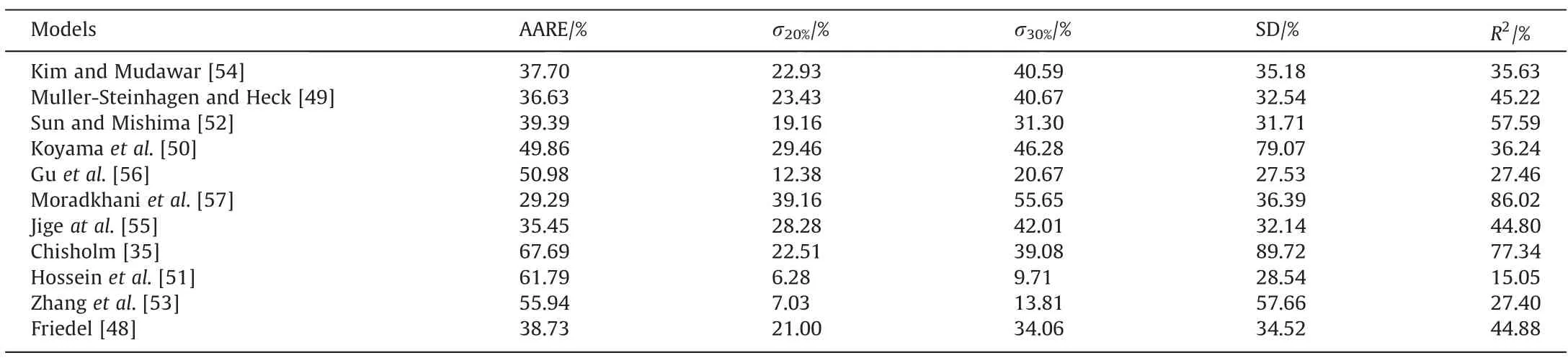
Table 1The results of literature correlations to predict the two-phase FPD of CO2

3.2. Novel predictive models for two-phase FPD of CO2

3.2.1. The background of the novel models

In this study, the well-known approach proposed by Lockhart and Martinelli [58] was utilized to model the FPD during twophase flow of CO2inside channels. According to this method, the two-phase FPD is determined by multiplying the liquid phase pressure drop by a two-phase modification factor,

where the Lockhart and Martinelli parameter [58]Xcan be calculated as,

In addition, the vapor and liquid phases pressure drops are defined as follows,

It should be noted that the single-phase friction factorfis determined by,

where the subscriptzcan be attributed to either the vapor or liquid phases.

Consequently, for modeling of the two-phase FPD through the Lockhart and Martinelli[58]approach,the Chisholm dimensionless parameterCshould be correlated with influential factors.However,in order to reach the highest level of accuracy,the most important variable in controlling the target function should be detected. For this reason, the Spearman’s correlation coefficients [59] between 14 dimensionless groups and the Chisholm parameter were determined,and a heatmap of the results has been presented in Fig.1.It should be noted that the maximum and minimum levels of correlation between two given factors are observed when the absolute values of Spearman’s correlation coefficient are 1 and 0, respectively.From the Fig.1,it can observe that the phases’density ratio,Rand reduced pressure,Predshow the highest relationships withC.In addition, the importance of vapor quality in controlling the Chisholm parameter is unneglectable, and it can also be included in the input variables. Among various forms of Reynolds number,the one corresponding to the two-phase flow,i.e.,Retphas the highest impact onCparameter.On the other hand,it has very high correlation with all other forms,and can satisfy their effects also.The two-phase Prandtl number,Prtpand Bond number,Boare another factors with high unique relationship withC, and it is therefore considered as an input variable.The Spearman’s correlation coefficient of the remaining factors with Chisholm parameter are less than 0.2, and often have high correlations with some of selected input variables. Hence, they are not included in the adjusted petameters used for modeling of the two-phase FPD of CO2.

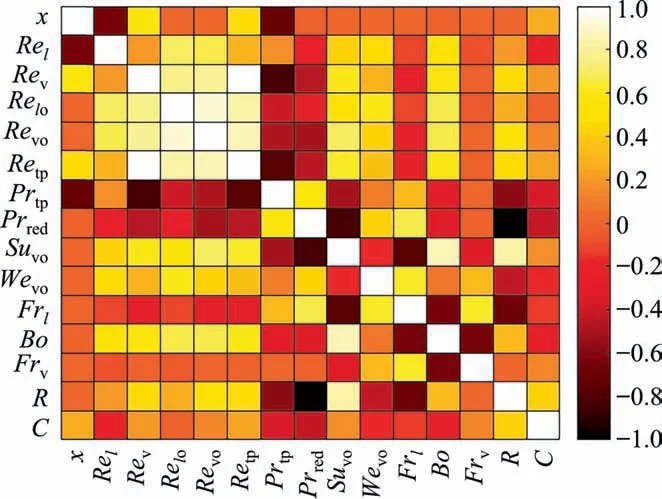
Fig.1. Spearman’s correlation coefficients between C and 14 dimensionless groups.

Fig. 2. The statistical error metrics corresponding to the novel intelligent models for predicting the FPD during two-phase flow of CO2.

According to the above discussion,the relationship between the Chisholm parameter and input variables in the novel models can be described as follow,

The analyzed ranges of the selected dimensionless groups covered by the present databank have been presented in Table 2. As seen, an extensive range of conditions during CO2two-phase flow has been enveloped by the collected databank, and it can be employed to design comprehensive predictive methods.

Table 2The analyzed ranges of dimensionless groups included in the novel models

3.2.2. Novel intelligent models for two-phase FPD of CO2

According to the strategy provided in the previous section, the collected databank was employed to design new models for FPD during two-phase flow of CO2based on the intelligent approaches of MLP, GPR and RBF. To achieve this goal, firstly, 956 data among those analyzed in this study,i.e.,80%of the databank,were used as the train dataset to design the predictive approaches. Afterward,the prediction capabilities of the designed intelligent models were tested and verified by the rest of data,i.e.,239 samples.The results of the novel approaches for predicting the two-phase FPD of CO2in training and testing stages have been sketched in Fig.2.This figure reveals that all three new models perform better than the literature correlations by far. According to the results, the GPR model ranks first in terms of precision and reliability, and has the AARE,SD andR2values of 5.48%, 8.38% and 98.80%, respectively for test data. Furthermore, its total accuracy is also higher than the other two model, which is another acknowledgment on its superiority.The next highly capable model is the one developed by the MLPapproach that shows the AAREs of 6.71% and 9.60%, andR2of 96.49%and 95.37%in training and testing steps,respectively.Such accurate results reveals that it can be considered as a proper alternative for the GPR model. Eventually, while the RBF model is the most exact approach during the training stage, it ranks third among all designed intelligent approaches in term of accuracy for the test dataset with AARE, SD andR2values of 12.74%, 21.32%and 92.28%, respectively. However, its predictions are noticeably superior to all literature correlations. Clearly, all models provide much reliable outcomes,and the values of FPD calculated by them have exact fitting to the measured data. Consequently, it can be found that the current intelligent approaches are efficient and reliable tools to estimate the FPD during two-phase flow of CO2inside channels.

3.2.3. New explicit correlation for two-phase FPD of CO2

Beside the newly developed intelligent models, the conventional approach of LAFM [60] was also implemented to derive an explicit correlation for FPD during CO2two-phase flow. Hence,the Chisholm parameter was correlated to the input dimensionless groups provided in Eq.(10).According to the theoretical investigations provided by Cheng and Wu [61] and Li and Wang [62], the surface tension significantly affect the two-phase flow when the Bond number is less than 3. However, by growing the Bond number, the influence of gravity force is enhanced, and overcomes the surface tension.This criterion has been used in various studies to model the two-phase FPD inside channels[56,63].As reported in Table 2,the values of Bond number analyzed in this study for twophase FPD of CO2vary between 0.03 and 125.93, which highlights the considerable differences between the impacts of surface ten-sion on the data.Consequently,the analyzed samples were splitted in two different domains by considering the influences of surface tension on two-phase flow, and a simple correlation for each domain was proposed by the LSFM approach. The final form of the novel correlation for two-phase FPD of CO2is as follow,

The statistical error metrics of Eqs. (11) and (12), including AARE,SD andR2are 19.76%,25.02%and 84.64%,respectively.Comparing these values to those of the literature correlations(Table 1)indicates a significant improvement in estimating the FPD during CO2two-phase flow inside channels. The predictions of the novel intelligent models as well as those of the LSFM correlation have been plotted against the measured data of the two-phase FPD of CO2in Fig. 3. As it is obvious, although the intelligent models provide much better performances, the outcomes of the LSFM model are also in satisfactory consistencies with the experimental values.

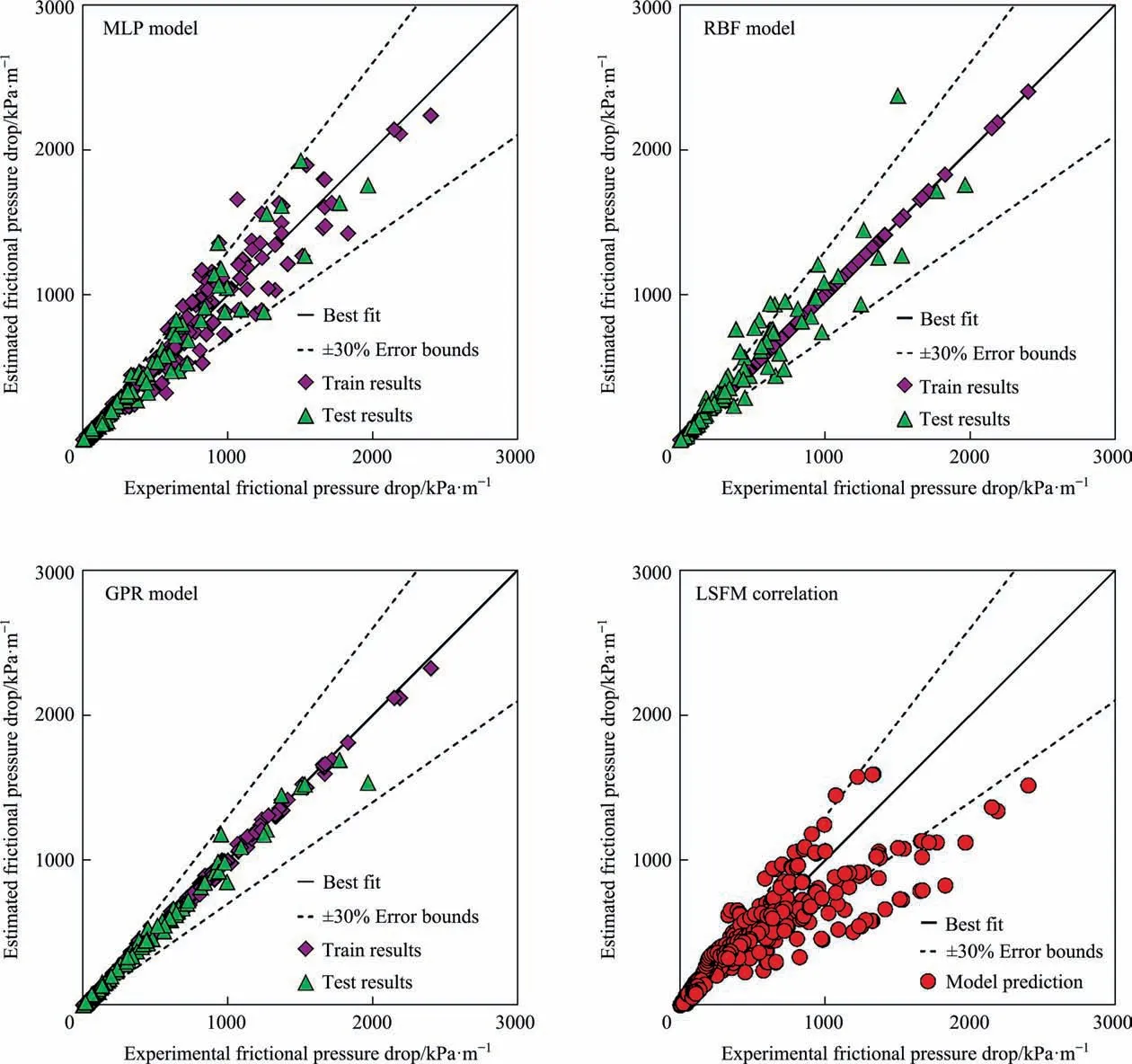
Fig. 3. Predictions of the newly proposed models against the actual values of the two-phase FPD of CO2.

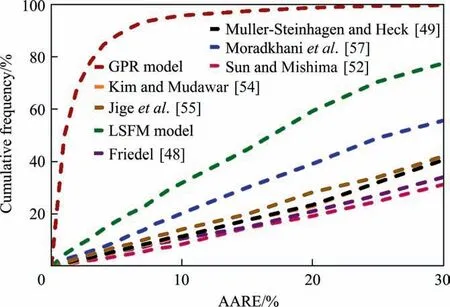
Fig.4. Cumulative frequency of novel and literature models for predicting the FPD during CO2 two-phase flow.

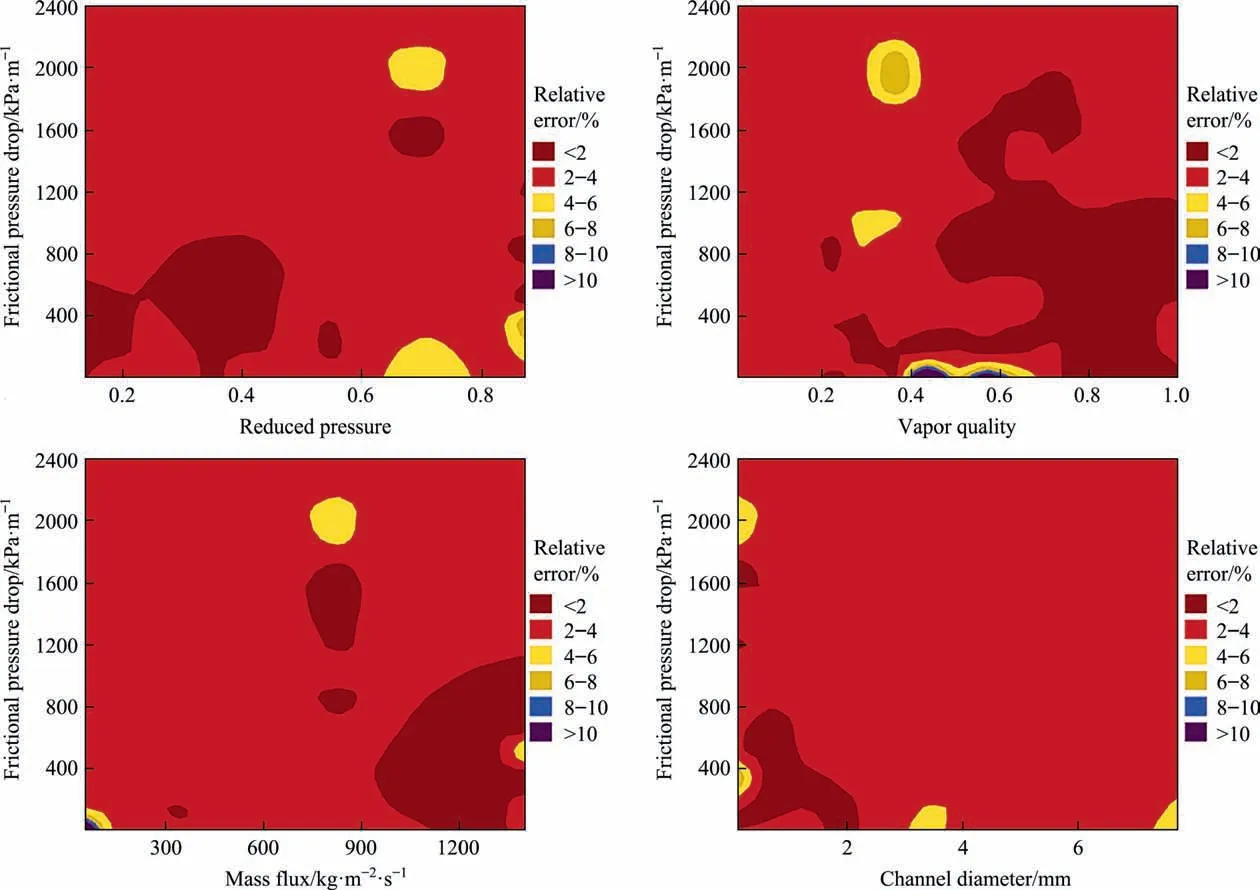
Fig. 5. Distribution of relative errors obtained by the GPR model to estimate the two-phase FPD of CO2 under various ranges of conditions.

3.3. Examining the reliability of the newly established models

To further acknowledge the reliability of the models established in this study for predicting the two-phase FPD of CO2, in this section, the graphical analyses of cumulative frequency and contour plot are utilized.

Fig. 4 compares the cumulative frequency of the most accurate intelligent approach,i.e., GPR, the new explicit correlation developed by the LSFM method and the top-six literature correlations for predicting the FPD during CO2two-phase flow.The cumulative frequency indicates the percentage of data predicted with relative deviations less than a given value.Hence,a more accurate model is expected to provide a higher cumulative frequency in lower levels of AARE. As observed, the cumulative frequency line of the GPRbased model is noticeably higher than the other predictive methods, and it predicts 68.45%, 88.12%, 95.82% and 98.83% of entire data with relative errors less than 2%, 5%, 10% and 20%, respectively. This is why the GPR model can be considered as the most capable approach to estimate the two-phase FPD of CO2. Among the explicit correlations, the best performance belongs to the one developed in this study based on the LSFM approach, which estimates most of data(approximately 60%of analyzed samples)with relative deviations less than 20%from the experimental values.The literature correlations have cumulative frequencies less than 50%at the AARE of 20%, which confirms their low capabilities for predicting the data of CO2. As a results, the novel predictive approaches can meet the existing requirement regarding the precise models for two-phase FPD of CO2.

The distribution of relative errors obtained by the GPR model in various ranges of reduced pressures, vapor qualities, mass fluxes and diameters has been depicted in the contour plot of Fig.5.This figure shows the precision of the model by a spectrum of colors varying between dark red to purple, which represents the AAREs less than 2% to exceeding 10%, respectively. As it is evident, the dominant parts of the contour plots have been enveloped by the light red and dark red colors, which means that the model estimates the two-phase FPD of CO2in most of analyzed ranges with AAREs up to 4%. On the other hand, some small areas with light yellow and dark yellow color can be observed, representing the AAREs between 4% to 8%. These areas mainly correspond to CO2two-phase flow with approximately 900 kg∙m-2∙s-1mass velocity inside small channel,when the reduced pressure and vapor quality tend to 0.7 and 0.4, respectively. There are also some insignificant points with relative errors from 8% to 10% (blue areas), which are related to very low mass fluxes and vapor qualities between 0.4 to 0.6. Overall, the current analysis is another testimony on applicability of the GPR model to estimate the two-phase FPD of CO2under different ranges of conditions.

3.4. Diagnosis of outliers

The highly deviated samples from the rest of data(outliers)are some problematic data points influencing the robustness of established models. The capable approach so-called William’s plot brings the outliers existing in the analyzed databank to light[64–66]. This method was employed to detect the outlying points included in the databank analyzed in the current study, and the results have been provided as Supplementary Material. According to the results, the majority of samples (96.32% of all data) have been allocated in the valid limit, proving the high reliability of the analyzed data and the proposed model. Moreover, the points recognized as good high leverage cover 2.51% of the data, which means that while they have relatively different conditions compared to the bulk of samples, the GPR model is able to estimate them precisely.Finally,there are only 14 suspected data in the current databank, which are much insignificant to influence the correctness of the novel models. As a result, the models established based on the current databank are robust and reliable tools for predicting the two-phase FPD of CO2inside channels.

3.5. Improvements made in the present models

3.5.1. Applicability for various channel sizes

The most common classification regarding the size of channels is that presented by Kandlikaret al.[67,68],in which theD=3 mm is defined as the boundary between conventional and mini/micro channels [69]. Employing this classification, the applicability of various models for predicting the two-phase FPD of CO2inside channels with different sizes was investigated, and the corresponding AARE values have been illustrated in Fig. 6. The figure implies the fact that the GPR model yields the superior predictions for both mini/micro and conventional channels with total AAREs of 2.11% and 4.02%, respectively. Another model with satisfactory results for different type of channels is the LSFM correlation(Eqs. (11) and (12)) developed in this study, which its AAREs in both cases are less than 20%. Among the literature correlations,the one proposed by Moradkhaniet al. [57] provides relatively good estimations for mini/micro channels with AARE of 26.99%.However,its results for conventional channels are far from reasonable range. The AAREs of the other literature correlations for both types of channels exceed 30%,and they have not enough capability to estimate the data of CO2. Consequently, the present analysis reflects the good improvements provided by the novel models in estimating the two-phase FPD of CO2inside channels with different sizes.

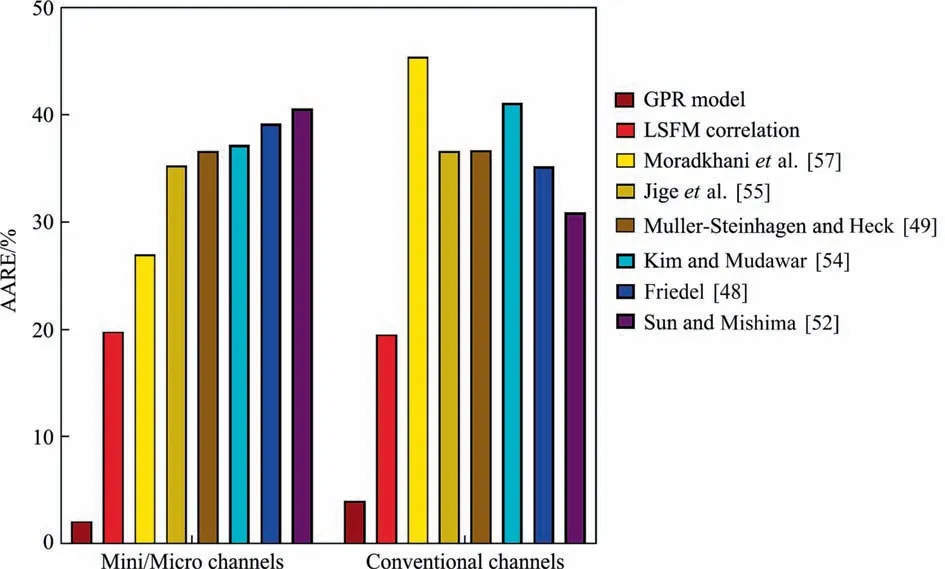
Fig. 6. AAREs of the novel and literature models for predicting the FPD of CO2 during two-phase flow inside channels with various sizes.

Fig.7. Distribution of data analyzed for two-phase FPD of CO2 in four different flow patterns.

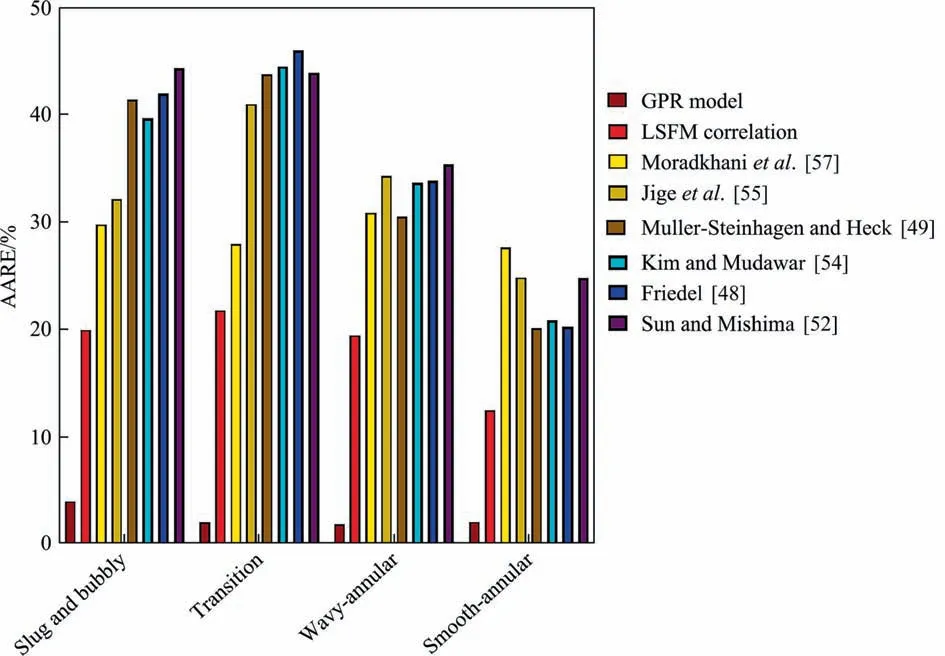
Fig. 8. AAREs of the novel and literature models for predicting the FPD of CO2 under various two-phase flow patterns.

3.5.2. Applicability for various flow patterns

Assessing the applicability for various flow pattern is another comprehensible benchmark to clarify the exactitude of the novel and literature models. Herein, the foregoing analysis was carried out by utilizing the methodology suggested by Kimet al. [70], in which four different flow patterns during two-phase flow are defined according to the values of modified Weber number,We*and the Lockhart and Martinelli parameter for turbulent flow,Xtt[20,71]. A visualization on the boundary lines between various flow patterns,and the distribution of collected data in each of them have been presented in Fig. 7. It is seen that the bulk of data have been allocated in the areas corresponding to transition and wavyannular flows. However, the slug and bubbly and smooth-annular flows also include sufficient number of data to examine the capabilities of the predictive models.

The bar chart provided in Fig.8 compares the newly developed models with literature correlations from the standpoint of precision for estimating the two-phase FPD of CO2under various flow patterns. The superiority of the GPR model to other predictive methods is obvious with AAREs of 3.98%, 2.01%, 1.82% and 2.04%,for slug and bubbly, transition, wavy-annular and smooth annular flow, respectively. These results are further attestations regarding the high potential of the novel intelligent approach. The new LSFM-based correlation is also the only explicit model that renders adequate precisions for all cases with AARE values varying between 12.48% for smooth-annular flow to 21.75% for transition flow. Hence, it can be used as a simple and efficient alternative for the intelligent methods. The literature correlations selected for this analysis provide relatively suitable predictions for smooth-annular flow with AAREs less than 30%.However,in other flow patterns,their predictions are highly deviated from experiential data. Thus, the newly established models are the only predictive approaches applicable for predicting the FPD of CO2under all two-phase flow patterns.

3.5.3. Predicting the physical attitudes corresponding to FPD of CO2

Another qualification that should be met by a robust predictive approach is the ability to describe the target function physical attitudes. In order to confirm this ability regarding the novel models,in the following, the impacts of reduced pressure, vapor quality,diameter of channel and mass flux on the two-phase FPD of CO2are studied through the outcomes of GPR model. For further embossing the superiority of this model to those available in the literature,the results of Moradkhaniet al.[57]as the most accurate existing correlation are also included in this assessment.

Fig. 9 demonstrates the variation of the two-phase FPD of CO2with reduced pressure and vapor quality under the constant mass flux of 1200 kg∙m-2∙s-1inside a tube with 0.529 mm inner diameter.A glance at the figure reveals the increase of FPD of during CO2two-phase flow by growing the vapor quality and reducing the reduced pressure. This behavior can be explained by boosting of the two-phase velocity difference caused by the foregoing changes.Although both GPR and Moradkhaniet al. [57] models correctly emulate the overall trends,the novel one agrees much better with the experimental data.

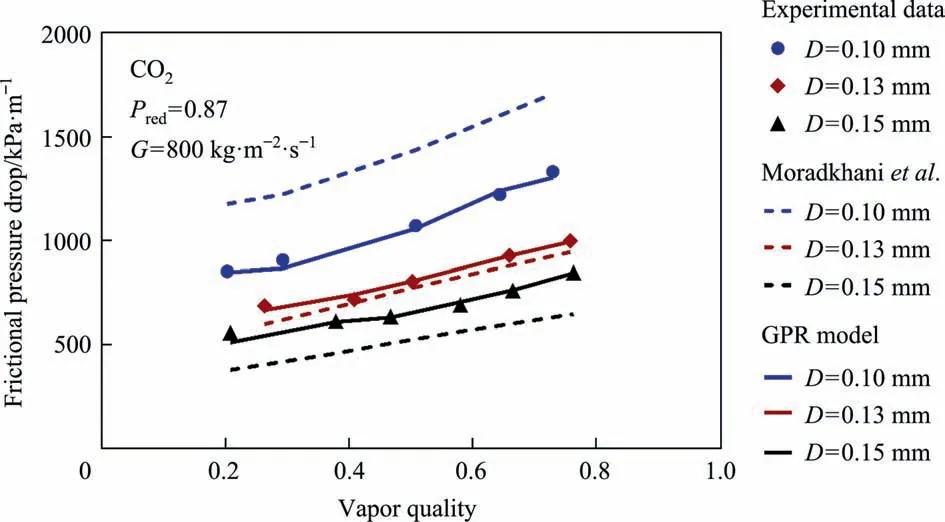
Fig. 10. Assessing the potential of the novel and literature models to describe the impact of diameter on the two-phase FPD of CO2.

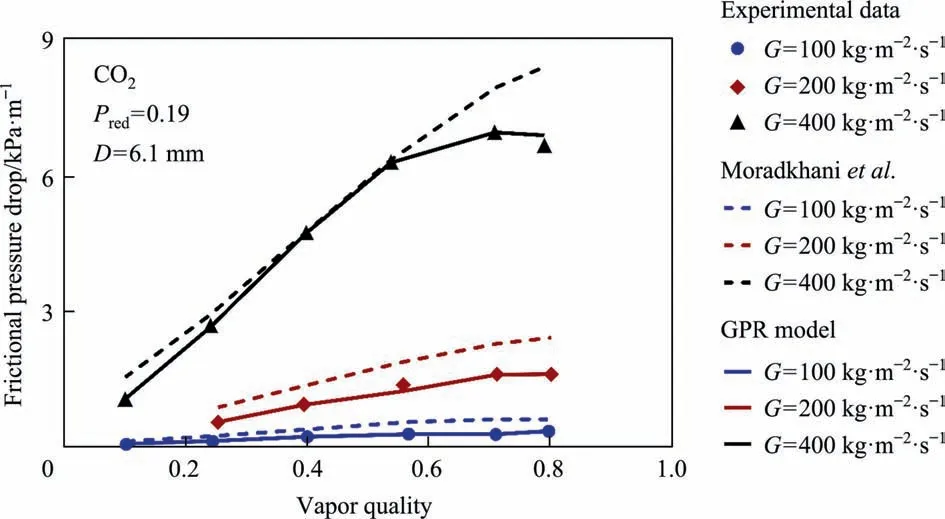
Fig. 11. Assessing the potential of the novel and literature models to describe the impact of total mass flux on the two-phase FPD of CO2.

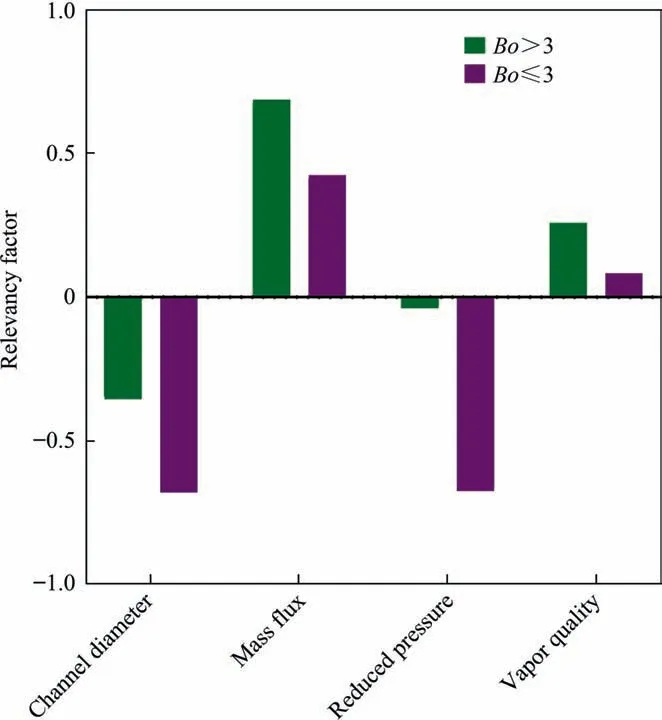
Fig.12. Relevancy factor between two-phase FPD of CO2 and the operating factors.

The alternation of the two-phase FPD of CO2with channel diameter has been described in Fig.10,while the reduced pressures and mass flux have been held at fixed values.As it is evident,the FPD of CO2experiences a dramatical enhancement by decreasing the tube diameter.The principal argument regarding this trend is amplification of velocity gradient caused by surface tension influences in smaller channels, which leads to higher shear stress and twophase FPD. The same physical attitudes are also provided by the outcomes of the models. However, there are much closer agreements between measured values and those calculated by the novel intelligent model.

Fig.11 epitomizes the change of two-phase FPD of CO2with the total mass flux. The results imply the intensive raise of FPD by increasing the total mass flux.In fact,the mentioned change tends the velocity of both liquid and vapor phases to enhance, and the friction force and two-phase FPD are augmented. Similar to previous investigations, the present results demonstrates the superiority of the novel model to that proposed by Moradkhaniet al.[57]for describing this physical attitudes.

3.6. Sensitivity analysis

In order to explain how the two-phase FPD of CO2is related to the operating parameters, the relevancy factors between the outputs of GPR model and reduced pressure, vapor quality, diameter of channel and mass flux were calculated by employing the Spearman’s correlation analysis[59,72]discussed in Section 3.2,and the outcomes have been sketched in Fig. 12. It is evident that the relevancies of FPD with mass flux and vapor quality are direct, while the reduced pressure and channel diameter have inverse relationships with FPD. However, the order of importance of factors at Bond numbers equals to or less than 3 is entirely different from that at higher Bond numbers. At scant Bond numbers, the channel diameter,reduced pressure and mass flux have substantial impacts on FPD of CO2, and they rank first to third, respectively in the standpoint of importance. However, the vapor quality inconsiderably affects the FPD under such condition.When the Bond number exceeds 3,the most influential factors are mass flux,diameter and vapor quality, respectively. Also, the results allude the negligible relationship between reduced pressure and FPD at the foregoing situation.Consequently,the present analysis affirms the argument provided in Section 3.2.3 regarding the significant differences between two-phase FPD of CO2in the mentioned ranges of Bond number, which stems from the influences of surface tension force.According to [73], two-phase frictional pressure drop of nitrogen refrigerant in mini channels is strongly influenced by surface tension.

4. Conclusions

The scope of this study was designing robust and comprehensive methods by which the FPD of CO2, as a safe and environmentally friendly working fluid, during two-phase flow inside heat exchangers can be predicted. A widespread FPD databank, comprising 1195 measured samples adopted from 10 studies was utilized to reach this target. The modeling process was performed by employing the intelligent computer-aided methods, including MLP, GPR and RBF. Besides, the conventional modeling approach of LSFM was also applied, so that a novel simple correlation was proposed by considering the surface tension effects on the twophase FPD of CO2.The main conclusions of this study can be listed as follows:

• The literature models exhibited unsatisfactory outcomes for the two-phase FPD of CO2due to strange properties of CO2compared to the other working fluids. Among them, the superior results were obtained by that developed by Moradkhaniet al.[57] with AARE of 29.29% and SD of 36.39%.

• Six dimensionless groups (x,Retp,Prtp,Pred,BoandR) were chosen as the most effective input variables through the Spearman’s correlation analysis. Then, three intelligent models were designed by inspiring the theoretical approach of Lockhart and Martinelli, which were superior to the literature correlations by far. It was found that the GPR model surpasses the others from the standpoints of reliability and precision with AARE,SD andR2values of 5.48%,8.38%and 98.80%,respectively for test data. The models designed based on MLP and RBF approach also presented appropriate outcomes with AAREs of 6.71% and 12.74%, respectively for the testing process.

• The novel LSFM-based correlation also provided opportune estimations for the two-phase FPD of CO2with AARE, SD andR2of 19.76%, 25.02% and 84.64% from the entire data.

• The truthfulness of various models was examined by employing an array of statistical and visual descriptions. The contour map and cumulative frequency analyses implied that the recently proposed methods estimate the majority of analyzed samples in a broad range of conditions with very high precisions. Also,the validity of collected data was affirmed through the William’s plot, since there was just 14 outlying points in the databank.

• Beside the applicability for various channel size and two-phase flow patterns, the recently developed models favorably described the physical attitudes corresponding to two-phase FPD of CO2under a variety of operating conditions.

• According to the sensitivity analysis accomplished through the outcomes of the GPR model,the operating factors with the highest influences on the two-phase FPD of CO2at scant and high Bond numbers were the channel diameter and total mass flux,respectively.

Overall,the recently proposed models provided high precisions for the analyzed ranges of conditions. Additional experimental investigations on the two-phase FPD of CO2are desired to further assess the prediction capabilities of the models,or to modify them if necessary.

Data Availability

Data will be made available on request.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was funded by the National Foreign Expert Project(G2022178023L).

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.cjche.2023.05.001.

Nomenclature

BoBond number,Bo=gD2(ρl-ρv)/σ

CChisholm parameter

Dchannel hydraulic diameter, m

dP/dzpressure drop, Pa∙m-1

ffriction factor, defined by Eq. (9)

Frvvapor Froude number,Frv=G2/

Gtotal mass flux, kg∙m-2∙s-1

g acceleration due to gravity, m∙s-2

kthermal conductivity, W∙m-1∙K-1

LaLaplace number

Pccritical pressure, Pa

Pssaturated pressure, Pa

Predreduced pressure,Pred=Ps/Pc

Prlliquid Prandtl number

Prtptwo-phase Prandtl number,Prtp=xPrv+(1-x)Prl

Prvvapor Prandtl number

Rphases’ density ratio,R=(ρl-ρv)/ρl

Relliquid Reynolds number,Rel=G(1-x)D/μl

Reloliquid only Reynolds number,Relo=GD/μl

Retptwo-phase Reynolds number,Retp=Rel+Rev

Revvapor Reynolds number,Rev=GxD/μv

Revovapor only Reynolds number,Revo=GD/μv

Suvovapor only Suratman number,Suvo=ρσD/μ2

We*modified Weber number

Wevovapor only Weber number,We=G2Dh/ρvσ

XLockhart–Martinelli parameter

XttLockhart–Martinelli parameter for turbulent flow

xvapor quality

μ dynamic viscosity, Pa∙s

ρ density, kg∙m-3

σ surface tension, N∙m-1

Subscripts

F frictional

lliquid

s saturated

v vapor

tp two-phase