传统的概率计算方法融入全概率公式的研究

阚永志

(辽宁工业大学 理学院，辽宁 锦州 121001)

一、问题的提出与分析

“概率论与数理统计”这门数学课程在高等院校的所有数学课程中最灵活、应用最广泛，在理论上具有一定的抽象性，学好它有助于提高学生的数学思维能力，使其更有效地奠定必要的数学基础。学生在学习概率论时，普遍感到计算公式具有一定的灵活性、重复性以及计算上的繁琐性，而且在解决实际问题时，由于对基本概念、基本理论及基本方法的理解不深或掌握不熟练，难以入手，这就使学生逐渐失去学习的兴趣和信心。

在“概率论与数理统计”的教学中，概率的计算一直是非常重要的问题，在涉及比较复杂概率的计算时，全概率公式早已成为常用的、必不可少的有效计算工具，在概率计算中具有相当广泛的应用。但由于全概率公式的抽象性，且很多学生对该公式的使用条件以及如何根据实际问题构造样本空间的划分还一直感到困惑，所以它也是概率计算方面的难点之一，学生对它更加难以理解和掌握。另外，大众化的教育也使学生对基础知识的掌握不扎实，因此，学生灵活应用基础知识的能力欠缺，这也是教学中普遍存在的问题。

针对全概率公式的学习方法及应用已有很多的研究[1-7]，有些学者也对该公式进行了必要的推广[8-11]。如有些文献阐述了它在经济领域及医疗诊断方面（如经济决策、产品检验、传染病的诊断）的应用，有些文献阐述了它在求分布函数时的应用等。

但上述文献研究和讨论的都是全概率公式在哪些方面具有广泛的应用，而本文阐述的是在同一概率计算的教学中，除了直接利用传统的概率计算方法外，还要会使用全概率公式，以解决全概率公式应用的不足。在概率计算的不同方法上，让学生进一步体会全概率公式另一方面的重要应用。这样一来，概率论的教学方法会有一定程度的改进，学生对概率论的学习兴趣也会逐渐提高。

有关定义及计算公式：

有限可加性[12]8若A1,A2,…,An是两两互斥的事件，则有

减法公式[12]8

乘法定理[12]16设P(A)＞0，则

定义[12]17设S为试验E的样本空间，B1,B2,…,Bn是E的一组事件，若

（i）B1,B2,…,Bn两两互斥，即BiBj=φ,i≠j,i,j=1,2,…,n；

（ii）B1∪B2∪…∪Bn=S，则称B1,B2,…,Bn为样本空间S的一个划分。

定理[12]18设试验E的样本空间为S，A为E的事件，B1,B2,…,Bn为S的一个划分，且P(Bi)＞0(i=1,2,…,n)，则有全概率公式

全概率公式是把事件A的概率分成有限个比较容易计算的概率之和。在具体分析问题的过程中，把Bi看成A发生的原因，A是结果，即由“原因”找“结果”。也就是说，一个结果A的发生总是与某些前提条件（或原因、因素或前一阶段结果）Bi有联系，那么在计算P(A)时，用Bi对A进行分解：，应用全概率公式计算P(A)，我们常称这种方法为全集分解法。

基于篇幅所限，本文主要列举几个具体实例加以讲解。

二、实例应用讲解

（一）根据样本空间的适当划分融入全概率公式

例1[13]有一个问题，甲先答，答对的概率为0.4，如果甲答错，由乙答，答对的概率为0.5，求问题由乙解答出的概率。

解析由题意分析，乙解答出问题需满足“甲答错，且问题由乙解答出”，所以，若设事件A={甲答对问题}，B={乙答对问题}，则P(AB)=0，且根据式（2），得所求的概率应是事件和B的积事件的概率P(B)=P(B)-P(AB)=P(B)，显然，即为事件B的概率P(B)。

方法二 直接利用式（4）

上述两种方法都是我们在概率计算的教学中使用的传统方法，其中第二种方法比较简便。

如果从下面一种思路来考虑，那么就有不同的解法，即考虑事件B的发生与事件A及都有关联，此时可用A及对B进行分解：

B=B(A A)=BA BA；或者将该试验的样本空间构建为互斥事件A及，则A,A构成样本空间的一个划分，而事件B为该试验的事件，从而就可应用全概率公式（5）求P(B)。下面给出具体解法：

方法三 由于P(A)=0.4，P(B|A)=0，P(B|)=0.5，故由式（5）可得

这样就将全概率公式应用于概率计算的教学中，使学生不仅会用传统的概率计算方法，而且也会用全概率公式。对于本例，虽然全概率公式不是最简便的方法，但从中可领悟全概率公式使用的奥妙所在。

（二）抽签模型中传统的概率计算方法融入全概率公式

例2袋中有4 个白球，3 个黑球，从中无放回地取三次，每次取1 球，求第二次取到白球的概率。

解析显然本例属于比较简单的抽签模型中概率计算问题，也是常规题型，几乎所有的有关概率论教材及参考书都有讲解，且传统的讲解方法有多种，如利用有限可加性及古典概率计算公式等，结果都是4/7。

方法二 把无放回地取三次球作为随机试验，即从袋中任意取出3 个球为随机试验。由于共有A37种取法，每种取法为一基本事件，所以样本空间包含的基本事件总数为A37。事件A={第二次取到白球}包含的基本事件总数为4×3×2+4×3×3+3×4×3+3×2×4=120。故依式（3），所求的概率为P(A)=120=47。

方法三 第二次取到白球应从4 个白球中任取1 个，共有4 种取法；其余两次为从余下的6 个球中任取2 个，共有种取法。故依式（3），所求的概率为P(A)=。

方法四 假设试验为不放回地一件一件取走，则样本空间包含的基本事件总数为7!。事件A的发生等价于“在4 个白球中任取1 个放在第二个位置上，余下的6 个球随意排在其余位置”，则A包含的基本事件总数为·6!。故依式（3），所求的概率为

。

除上述传统的讲解方法外，本文再介绍一种方法——应用全概率公式（5）。我们仍从样本空间不同构建方法的角度去探讨。

方法五 设事件A={第二次取到白球}，Bi={第一次和第三次取到的 2 个球中恰有i个白球}(i=0,1,2)。易知B0,B1,B2是样本空间的一个划分，且有

故由式（5），得

（三）求边缘分布律时融入全概率公式

若某事件A依赖于某个离散型随机变量X，或者说某事件A的发生与事件{X=xk}（k=1,2,…,n）都有关联，则由式（5）得全概率公式

例3从数1,2,3,4 中任取1 个数，记为X，再从1,…,X中任取1 个数，记为Y，求P{Y=2}。

解析若能求得二维离散型随机变量（X,Y）的联合分布律，则很容易求得边缘分布律中概率P{Y=2}，下面即关于求边缘分布律教学中传统的讲解方法。

方法一 当i＜j时，P{X=i,Y=j}=0；当i≥j时，P{X=i,Y=j}=P{X=i}P{Y=j|X=i}=1/4×1/i，即（X,Y）的分布律，见表1。

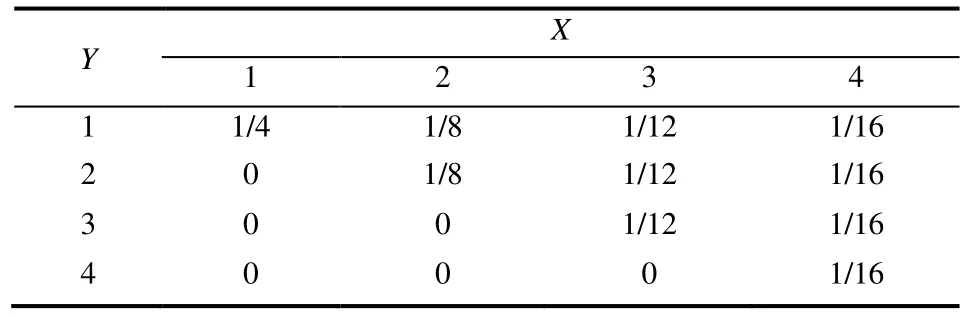
表1 （X,Y）的分布律

故P{Y=2}=0+1/8+1/12+1/16=13/48。

如果不仅考虑到Y的取值依赖于X，且能深一层想到事件{Y=2}，可做如下全集分解：

对于本例，因为方法二避免了联合分布律的求解过程，所以应用全概率公式求边缘分布律中概率的方法就更加简便。这样一来，学生对全概率公式的使用条件以及如何构造样本空间的划分自然就有了进一步的认识，这也有助于增强学生学习概率论的信心。

三、结束语

本文通过几个具体实例说明全概率公式在解决实际问题中有着广泛的应用，而且它在应用上非常灵活有效，能够解决日常生活中很多难以解决的繁琐问题。在应用时，需要将试验的样本空间进行恰当的划分，将很复杂的问题化为若干个简单事件的和，最后利用全概率公式就能得到所要的结果。全概率公式的灵活融入不仅能让每位学生真正体会其内涵所在，而且也有助于激发学生学习的兴趣。