基于改进遗传算法的解剖类课程组卷研究

张迪, 容道君, 马勇超

(1.西安欧亚学院, 信息工程学院, 陕西, 西安 710000; 2.西安交通大学, 电子信息学部, 陕西, 西安 710000)

0 引言

IT技术的不断发展使医学领域在检测、治疗、诊断等方面达到了前所未有的高度,在医学教学方面,基于3D技术构建的人体解剖模型有力支持了解剖类课程的教学需求[1],在尸体资源相对缺乏的环境下具有重要实际意义。各大医学院在局部解剖、系统解剖学等基础课程的教学中往往面对较大的学生量,教师反馈学生作业情况时耗时较多,且解剖学课程大量的知识点需要学生反复记忆、大量练习以扎实基础,所以教师在此类课程建设中更适宜基于IT技术的支持,一方面积累试题资源库,另一方面建立智能组卷系统,基于各类优化算法设定知识点、试卷难度更加科学、高效地生成作业及试卷,减少时间和空间上对学生学习环境的约束,提高学生学习效果[2]。智能组卷系统的核心技术是生成试卷的算法,算法的性能决定了生成试卷的开销大小以及是否满足教师设定参数的要求。因此,研究试卷生成算法在解剖类课程题库中的性能表现,对解剖类课程教学提升学生学习效果,以及相关类型的课程教学有重要意义。国内外目前应用的算法有随机选取法、回溯试探法、遗传算法、知识图谱的多策略方法[3]等。

本文选取遗传算法生成试卷,遗传算法(GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的,是一种通过模拟自然进化过程搜索最优解的方法。与传统组卷算法相比,遗传算法具有全局搜索特性、复杂问题简单化等特点而被广泛应用于试卷生成中。

然而,遗传算法作为一种智能优化算法存在一些局限性,如迭代过程缓慢和早熟收敛等问题,本文基于此类问题提出了动态变异的改进方案,以提升算法的性能。

1 解剖课程试题库

系统解剖课程包括骨学、关节学、肌学、内脏学总论、消化系统、呼吸系统、泌尿系统、生殖系统、腹膜、会阴、心血管系统总论、心等章节,局部解剖课程包括头部、颈部、腹部、盆部与会阴等章节,题目类型设置为单选题、多选题、识图题,题目类型的设置满足学生加深知识记忆的同时,通过对图片更深入形象地理解人体各部位的解剖性状。肝门静脉和肩部识图题,如图1所示。

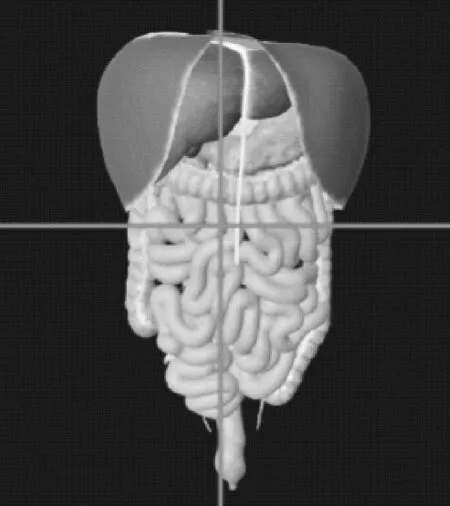
图1 肝门静脉和肩部识图题

识图题的图片来源于课题研究团队研发构建的系统解剖和局部解剖的骨骼、骨连结、肌肉、动脉、静脉、神经系统、呼吸系统、消化系统、泌尿系统、淋巴系统、皮肤等三维模型3700多个,设计试题3000多道。

表1 试题库

2 遗传算法设计与数学模型

遗传算法通常先初始化随机产生一个包含20张试卷个体的集合作为初始种群,然后对每一个试卷个体计算相应的适应度,用来衡量一个试卷个体的优劣。操作步骤包括选择、交叉、变异、计算适应度。首先是对初始化种群进行选择方法筛选优秀个体作为父代,再对筛选过后的父代个体进行交叉方法产生子代,然后进行个体变异操作,经过选择、交叉和变异后判断是否有满足需求个体产生,否则一直循环重复选择,交叉,变异操作,直到迭代次数达到规定次数,或者有达到满足要求的个体产生。

(1) 试卷编码

试卷编码采用实数编码方案,将一份试卷映射为一个染色体,试卷里每一道题映射为一个基因,题号即为基因的值,每一道题在数据库内有难度与对应知识点两个参数,每种题型分段存放。由于题库庞大采用二进制编码需要对题库每一个题目进行编码,选中为1不选中为0,题库越大解码过程越久,所以本算法采用的是实数编码。

(2) 初始化种群

在初始化种群时,设产生初始种群A,a为试卷,w为试题[2]。

(1)

(3) 适应度函数的设计

试卷难度P指一张试卷的整体难度,k是试卷所含的题目数,Di和Si分别是第i题的难度系数和分数。

(2)

知识点覆盖率R是期望知识点个数除以试卷总知识点的并集,M是一张试卷所有题目知识点的并集,N是期望包含的知识点。

(3)

式中,适应度函数为F,知识点的覆盖率为R,试卷难度为P,用户期望难度为EP,其中f1为知识点分布的权重,f2为难度系数所占权重。当f1=0时退化为只限制试题难度系数,当f2=0时退化为只限制知识点分布。

(4)

(4) 选择算子设计

选择算子采用了最优选择方法,最优选择法模拟了自然界中适者生存的自然现象,直接从种群中获取适应度最高个体保留到下一代。最优选择法使种群中最优秀个体不经过交叉操作,把优良基因直接保留到子代,有效的对整体的进化方向起到较好的作用。适应度最高试卷L,a为试卷,F为适应度。

(5)

(5) 交叉算子设计

交叉算子采用了两点交叉,由两个父代随机获取两个点分成三段,每个父代选出一部分组成一个新的个体。采用两点交叉出现相同试卷个体的几率会比单点交叉明显降低。tp0、tp1为父代,进行两点交叉过程后生成子代tp01。

(6)

(7)

(8)

(6) 变异算子设计

变异算子在遗传算法中起到了很大的作用,变异能够让种群产生新的试题来保证种群的多样性,使劣质个体能变异后适者生存[4]。种群中每一张试卷每一道题进行概率变异,遍历每道题时随机产生一个数如果小于Z,就从题库抽取一道与变异题目类型相同的题目进行交换[5]。

(9)

如Z=0.085,an为试卷,wnk为一道题目,遍历到wnk时产生的随机值小于Z,就对wnk进行变异。

3 遗传算法的改进

3.1 改进变异算子

在突变算子中,由于每个个体的每个基因都有突变的的可能性,随着种群和个体基因的扩大,在变异概率过小时,会使重复迭代的次数增多,频繁的发生迭代很多次仍达不到期望的适应度[6],变异度过大会因为频繁的数据比对,造成迭代效率的下降,总体都会影响组卷的效率。因此,选择一个合适的变异概率,会极大的提高组卷的效率。

有研究表明,对于变异概率的选择,在0.1～0.001最佳,通过对该限定范围内概率的大量实验,得出使变异概率在区间[0.055～0.065]动态变换,会使迭代达不到期望适应度的概率大大减小,提升了迭代效率[7]。初始规定变异概率为0.055,当迭代出现重复适应度时,立即改变变异概率为0.065,促进变异更快,减少出现重复适应度而带来的开销,当适应度恢复正常的增长时立刻将变异概率调回0.055,提升迭代速度,进而改进算法效率。改进后的遗传算法流程如图2所示。改进的动态变异算法流程如图3所示。

ALGORITHM 1 Improved algorithm pseudo code

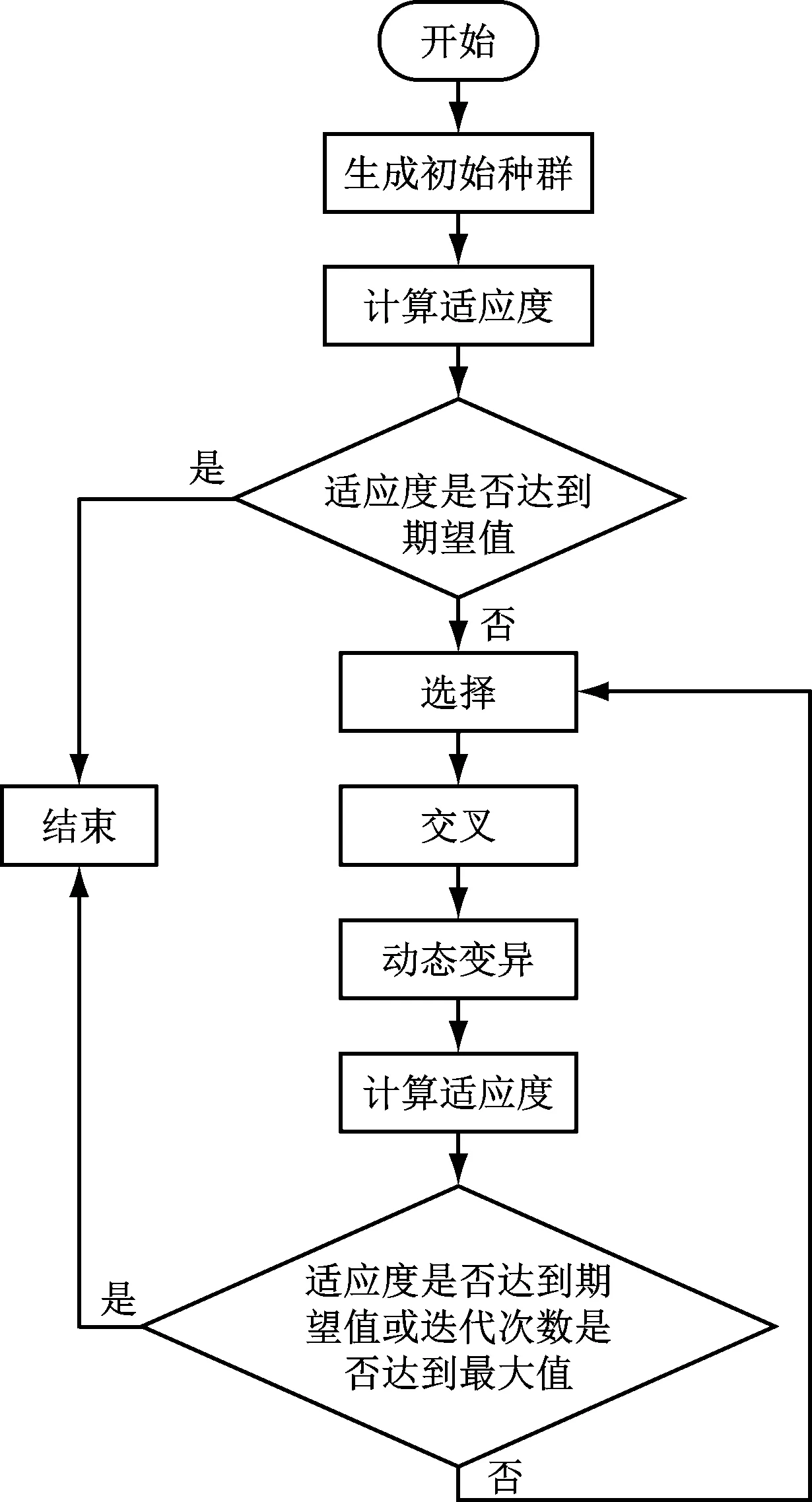
图2 改进后的遗传算法流程图

图3 改进的动态变异算法流程图

2 Paper max_paper;

3 //此代试卷个体

4 Paper paper

5 //变异概率

6 double mutationRate=0.055;

7 while(迭代次数未达到最大值and适应度未达到期望值)

8 {

9 //选择算子

The maximum number of persons with C/D lesions by TASC II were noted in the HS group; the minimum is in the EP group.

10 select();

11 //交叉算子

12 crossover();

13 //变异算子

14 mutate(max_paper,paper)

15 {

16 if(max_paper的适应度=paper的适应度)

17 {

18 mutationRate=0.065;

19 }

20 else

21 {

22 mutationRate=0.055;

23 }

24 }

25 //计算适应度

26 setAdaptationDegree();

27 }

4 实验验证

4.1 算例设置

本文通过维萨里公司提供的题库数据进行算法的验证,题库试题参数分别有题号、题型、知识点、题目、选项、答案、难度、分数。设置最大迭代次数为两百代,将变异概率从0.035～0.095每隔0.010分十组进行测试验证。

每组进行算法实验100次,分别测试不同变异概率对平均迭代次数、平均运行时间、最大连续重复迭代次数及迭代两百代仍未达到期望适应度的次数的影响,再将变异概率设置在区间[0.055～0.065]动态调整,记录变异概率从0.035～0.095每隔0.010分十组进行测试的实验结果如图4所示。从图4可以得出,当变异概率在0.055时,可以理解为当环境给予物种的压力处于中游的水平时,物种进化和适应环境的能力较好,产生适应环境的个体数目较多。图5记录了不同的变异概率下出现迭代至最大代数200代后仍然没有达到要求的适应度的个体出现的次数,可以看到曲线呈现出两边高中间低的趋势,说明变异概率在中游波动时,能够得到较好的个体,所以基于以上实验的数据结果,取区间[0.055～0.065]来设置变异概率。图6为变异概率在区间[0.055～0.065]内动态调整测试数据,可以发现测试100次迭代到两百代仍未达到期望适应度值的次数仅为6次,平均迭代次数仅为46次,最大平均重复连续次数仅为27次,耗时10.4 s比最好实验结果慢2.23 s,但获得了较多的优良试卷个体。

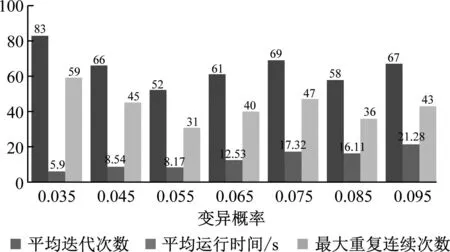
图4 不同变异概率测试结果

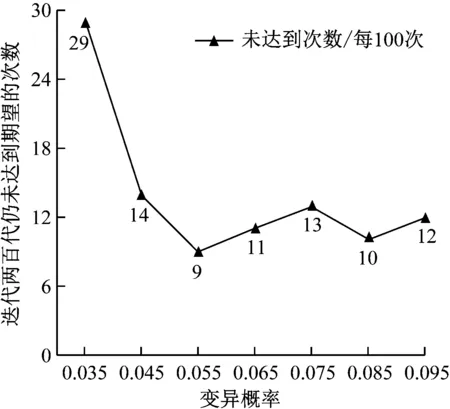
图5 不同变异概率下未达到期望次数

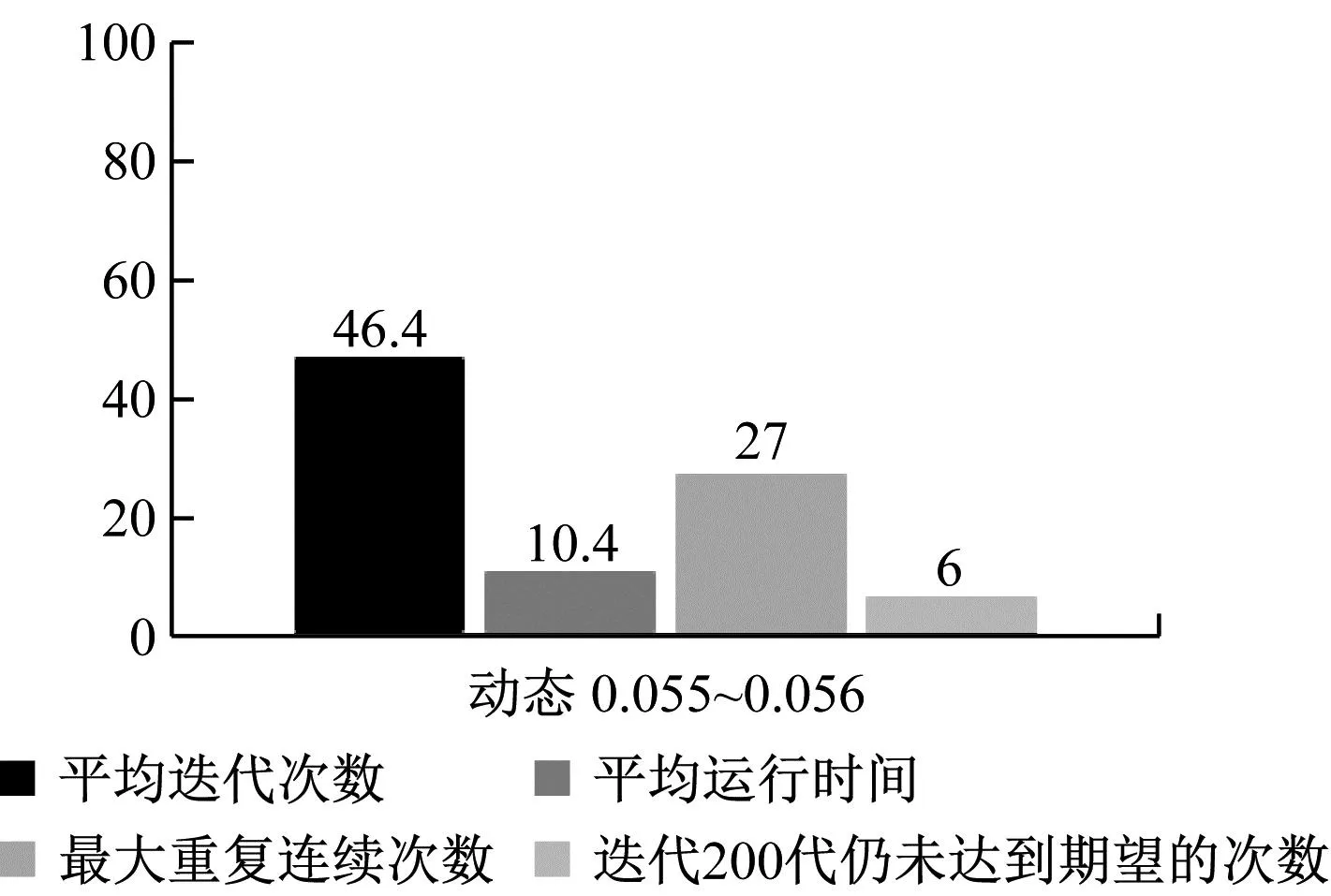
图6 动态变异概率下测试结果

4.2 算例结果与分析

实验发现,在单一固定的变异概率中,变异概率为0.055时,测试的不同概率对平均迭代次数,平均运行时间,最大连续重复迭代次数及迭代两百代仍未达到期望适应度的次数,实验结果相对最优,变异概率为0.065及0.085效果次之。

由图7可知,将在区间[0.055～0.065]动态调整的变异概率与最优的固定概率0.055、文献[1]中的固定概率0.085进行对比发现,动态的将变异概率在区间[0.055～0.065]调整会使得未达到期望适应度的次数降低,平均迭代次数更少,出现重复迭代的次数也大大减少,极大的提高了变异效率,提升了组卷的效率和稳定性。

图7 基准实例测试结果比较

5 总结

为生成最优试卷个体,降低时间成本和机器开销,建立了解剖课程题库模型,通过对遗传算法进行高效组卷问题的研究,引入了改进变异算子,模拟自然界环境压力的思想,找到适合产生更优个体的变异概率,从而提出区间内动态变异的方法,增强了寻优能力,相较于其他改进算法,求解的稳定性和速度得到提升,验证了本改进算法的有效性。