爆炸冲击波在扁平大空间内的传播规律

刘中辉， 匡志平

（1.同济大学 土木工程学院，上海 200092；2.浙江工业职业技术学院，浙江 绍兴 312000）

根据炸药在空气中爆炸时受周围环境约束程度的不同，爆炸可以分为自由空气中爆炸、近地空气中爆炸和内部空间爆炸。峰值超压、正相比冲量等是确定冲击波作用效果的主要参数，很多学者和机构，如Brode［1］、Henrych［2］、Wu等［3］和美国UFC 3-340-02手册［4］通过试验和数值模拟等方法给出了自由空气中爆炸时这些参数的计算公式。

近地空气中爆炸是指炸药在地面上方的爆炸，要求炸药距离地面的比例爆距不小于0.35m·kg—1/3。冲击波与地面碰撞后，根据入射角度的不同可以产生3种类型的反射：正反射、规则反射和马赫反射［5］。在炸药正下方的地面处，入射角为零，产生正反射，Henrych［2］和闫秋实［6］给出了正反射超压计算公式，对理想气体而言，正反射超压峰值接近于入射超压峰值的8倍，对真实气体而言，可达到13倍［7］。当入射角在零与与某个临界角（40°左右）之间时，产生规则反射，规则反射超压计算非常复杂，但当入射冲击波压力小于0.3MPa 时，可以采用正反射的公式计算［8］。当入射角大于临界角后，规则反射波与入射波在地面处开始合成为马赫波，入射波、规则反射波和马赫波的交点称为三波点，随着入射角的不断增大，三波点的位置逐渐升高。在三波点轨迹线下方区域，压力时程曲线有一个波峰，在上方区域有2个波峰［9］，利用这一特点，郭炜等［10］对三波点的位置进行了试验研究。此外，廖真等［9］研究发现马赫杆顶部的超压峰值仅为底部的67.6%～80.3%。

发生内部爆炸的空间主要有：单间或多间密闭房间、机库、舰艇舱室、弹药库、地铁车站、坑道、洞室、地下停车场等［11-12］。其中，密闭容器、弹药库、舰艇舱室、建筑房间等多由单个或多个密闭或半密闭空间组成，将发生在这类空间内的爆炸统称为有限空间内部爆炸［13］。在有限空间内发生爆炸时，准静态压力不能忽略，且在某些工况下是导致结构破坏的主要原因［14］。Baker［15］提出了内爆炸荷载多三角形脉冲估算法，该方法的准确性得到了部分工况的验证［11，16］。张舵等［17］指出Baker 的三脉冲模型理论上只适用于一维或二维问题，无法很好地适用于箱型结构等较复杂的情况。夏志成等［18］指出准静态压力随着装药量容积比m/V的增加而增加，王鑫等［12］、张明明等［19］给出了准静态压力的计算公式。邬玉斌等［20］应用LS-DYNA软件研究了地下建筑某房间产生的爆炸冲击波在邻近房间的传播情况。周晓青等［21］应用AUTODYN 软件研究了地下室发生爆炸后，冲击波沿不同竖向通道传播到地表后的分布情况及引起地面的震动情况。此外，一些学者对地铁车站内的爆炸进行了数值模拟研究，采用的软件主要为AUTODYN［22-25］和LS-DYNA［26-28］，研究普遍发现，爆炸冲击波最初以近似球面的形状传播，到达2～3 倍［22，24-25］柱间距的位置后，近似以平面的形式传播。在距爆源较近处，爆炸冲击波仅有一个显著的超压峰值，其他峰值相对很小；距离爆源稍远处，爆炸冲击波的超压峰值降低，但有多个峰值，且峰值大小呈递减趋势［22，27］；柱对其附近区域冲击波的超压峰值影响较大，但对其整体传播规律影响不大［23，26］。

可见，目前对于自由空气中爆炸和近地空气中爆炸的研究已经比较全面，对这2 种爆炸环境下冲击波的传播规律也认识得比较清晰；对于小型密闭和半密闭空间内爆炸的研究也比较多，发现了准静态压力在这种环境下是不能忽略的，并给出了计算公式；对地铁车站、隧道等较大空间内爆炸的研究也已经开始，并取得了一定的成果。但对内部布置了大量柱且高度远小于长度和宽度的地下停车场和地下大型商场等扁平大空间内爆炸的研究却鲜见报道。这类扁平大空间的显著特点是高度远小于长度和宽度，因此，发生内部爆炸时冲击波将在空间底面和顶面间来回反射，并不断向远处传播，这种传播特性既不同于自由空气中爆炸和近地空气中爆炸，也不同于密闭、半密闭空间内爆炸，同时，与地铁车站、隧道等长方体形大空间内爆炸也不尽相同。研究爆炸冲击波在扁平大空间内的传播规律既可以丰富人们对冲击波传播特性的认识，又可以为峰值超压估算和人员伤亡预测提供依据。鉴于此，采用AUTODYN 软件分析了扁平大空间中间位置地面处发生爆炸后冲击波在扁平大空间内的传播规律，给出马赫波阵面超压恒定位置的计算公式和该位置的最大超压计算公式以及任一点沿高度方向平均最大超压计算公式。

1 数值分析模型

某典型扁平大空间地下停车场平面图如图1所示，图中小方形代表柱。根据文献［23］和［26］以及笔者的前期分析结果，柱对爆炸冲击波在扁平大空间内的传播规律影响较小，因此，可以去掉柱，采用AUTODYN软件提供的Euler2D多物质二维轴对称矩形模型［29］对爆炸冲击波在扁平大空间内的传播规律进行分析，如图2 所示。该模型涉及三硝基甲苯（Trinitrotoluene，TNT）和空气2 种物质，TNT 为半球形，由于轴对称性在模型中用1/4 圆表示。模型的上下边界都是刚性，用于模拟地面和顶板，模型左侧设置了流出（flow out）边界条件，允许空气流出，从而模拟大空间。

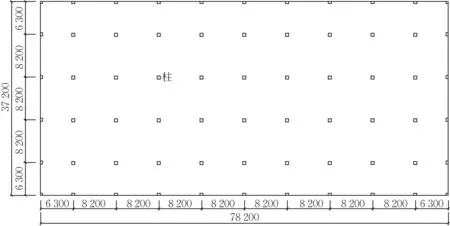
图1 典型扁平大空间地下停车场平面图（单位：mm）Fig.1 Plan view of a typical flat large space underground parking lot（unit：mm）

图2 半球形TNT扁平大空间内爆炸二维轴对称矩形模型Fig.2 2D axisymmetric rectangular model of hemispherical TNT blast in flat large space

TNT采用JWL状态方程［9，30］，如式（1）：

式中：p为静水压力；V为相对体积；E为能量密度；A、B、R1、R2、ω均为材料常数。当炸药爆炸后体积大于其初始体积的10倍后，程序自动将其状态方程转化为理想气体状态方程进行计算。方程中各参数均采用AUTODYN 软件默认值。其中，TNT 的初始密度为1.63g·cm-3，其他材料参数采用Lee等［31］给出的值，如表1所示。

表1 炸药材料参数Tab.1 Parameters of explosive material

2 爆炸冲击波在扁平大空间内的传播特性

空气采用理想气体状态方程［9，32］，如式（2）：

式中：p为静水压力；γ为绝热指数；ρ为质量密度；E为能量密度。各参数值采用AUTODYN 软件默认值，如表2所示。

表2 理想气体材料参数Tab.2 Parameters of ideal gas material

模型高度H为3.6m，长度为40m，沿长度方向每隔5m设置一列测点，每列各测点与地面的距离分别为0、0.25H、0.50H、0.75H、1.00H，即：0、0.9、1.8、2.7 和3.6m。爆炸TNT 当量分别采用1、5、8、27、64、125、343 和512kg。结合文献［33］给出的最佳网格尺寸确定方法，综合考虑各种爆炸工况统一取网格尺寸为20mm。文献［33］已证实了采用AUTODYN软件提供的Euler2D多物质二维轴对称矩形模型对地面爆炸进行模拟的准确性。

以5kg爆炸TNT 当量为例，给出爆炸冲击波在扁平大空间内的传播过程和部分测点的压力时程曲线，分别如图3和4所示。

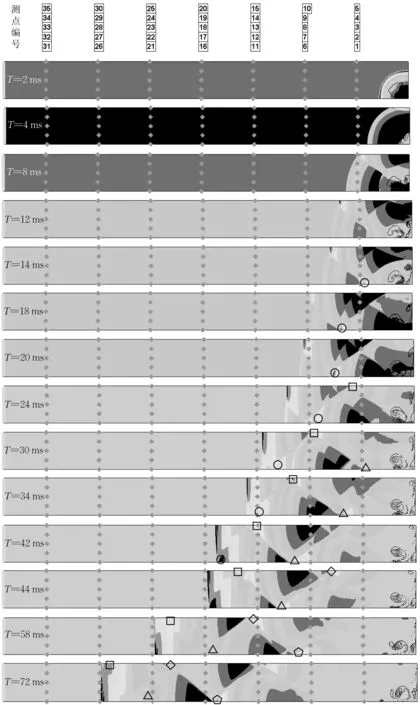
图3 爆炸冲击波在扁平大空间内的传播过程Fig.3 Propagation process of shock waves in flat large space

由图3 可见，爆炸冲击波开始以球面的形式向外传播，首次碰到顶板后发生了正反射，此时入射角和反射角均为零，反射波竖直向下传播。随着入射波不断向前传播，其在顶板处的入射角不断变大，反射角也相应变大，反射波的传播方向由竖向逐渐变成左下方向。当入射角大于某个临界值40°～ 70°［2］后，反射波在水平方向的速度分量大于入射波，因此，反射波追上了入射波，并与其合成了首个马赫波。由于马赫波的速率大于入射波的速率，随着时间的推移，马赫波的范围不断扩大，该马赫波范围称为马赫杆。马赫杆经过区域的压力时程曲线为单峰值，其外侧的区域为双峰值，分别为入射超压和反射超压引起，且单峰值较双峰值压力大很多。

结合图3，对图4中各测点压力时程曲线峰值对应的冲击波类型描述如下。

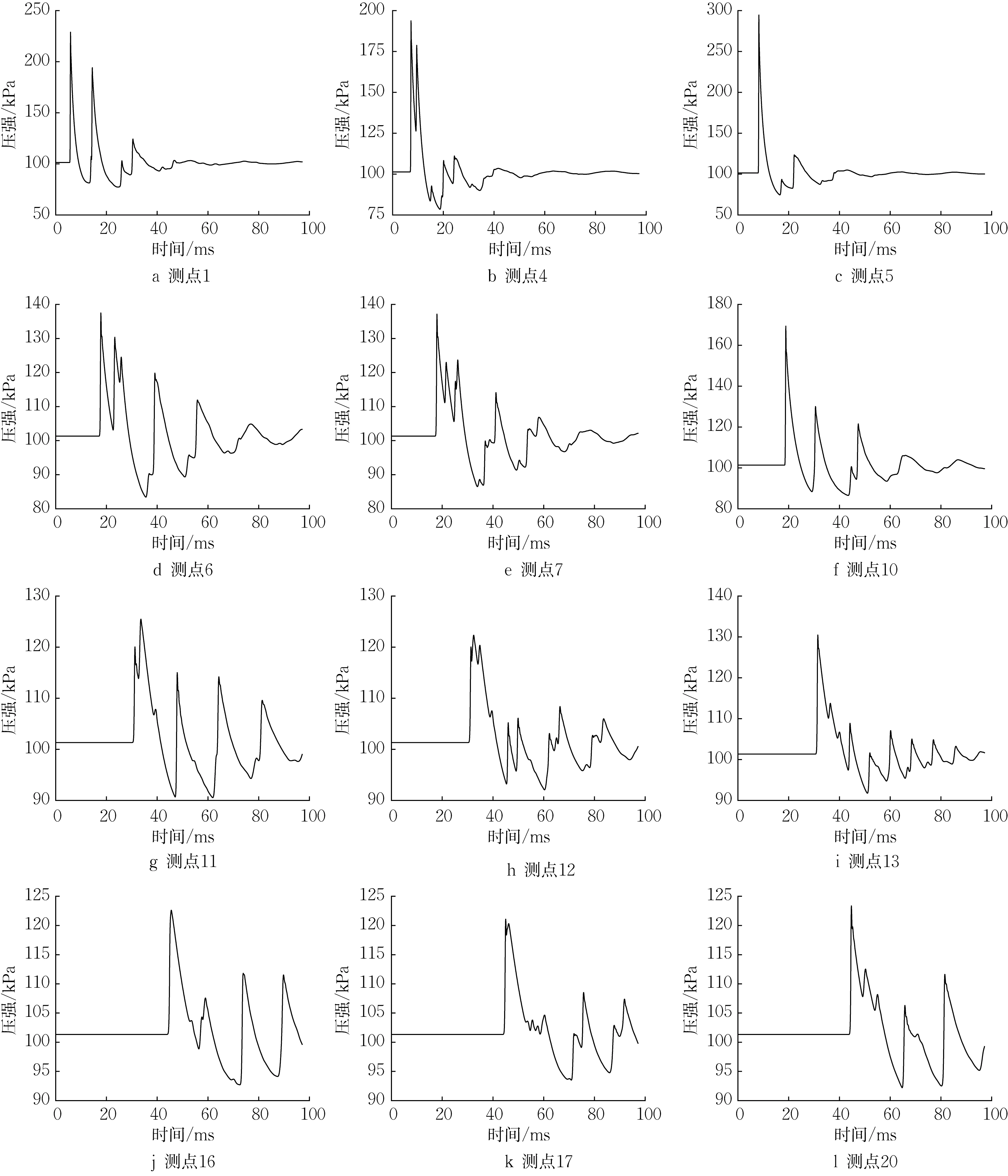
图4 部分测点的压力时程曲线Fig.4 Pressure time history of some gauges

图4测点5的第1个峰值是马赫波产生的，测点4的第1和第2个峰值分别是初始入射波和顶板初次反射波产生的，测点1的第1个峰值是初始入射波产生的，第2 个峰值是顶板初次反射波和地面初次反射波形成的第2个马赫波产生的，该波在图3中T=14ms时已用圆圈出，该马赫波传播速率较首个马赫波大，但马赫杆高度一直不大。测点4 和测点5 在20ms左右的2个峰值分别是地面初次反射波和顶板二次反射波产生的。

测点6 和测点7 的前3 个峰值分别是由初始入射波、顶板初次反射波和第2个马赫波产生的，测点10的第1个峰值是由首个马赫波产生的，第2个峰值是由地面初次反射波和顶板二次反射波形成的第3个马赫波产生的，在图3 中T=30ms 时已用方框标记出，该马赫波传播速率较首个马赫波大，但马赫杆高度一直不大。

测点13 第1 个峰值是由首个马赫波产生的，如图3 中T=30ms 时所示，说明这个位置处首个马赫波已经覆盖13～15这3个测点，第2到第4个峰值是地面初次反射波、顶板二次反射波和地面二次反射波引起的，其中，地面二次反射波的前沿即第4个马赫波已用三角形标记出。12号测点前3个峰值是由初始入射波、顶板初次反射波和地面初次反射波产生的，第4和第5个峰值是由顶板二次反射波和地面二次反射波引起的。11号测点第1个峰值是由初始马赫波引起的，第2 个峰值是由第2 个马赫波引起的，如图3中T=34ms时所示，此时，第2个马赫波即将追上首个马赫波，第3个峰值是由第4个马赫波引起的。

测点16 第1 个峰值是由首个马赫波引起，说明首个马赫波已经覆盖整个竖向空间，且第2 个马赫波已经在这个位置追上首个马赫波，第2 个峰值是由第4个马赫波产生的。测点17的前2个峰值挨得很近，是首个和第2个马赫波产生的，说明在这个位置处第2个马赫波即将追上第1个马赫波，第3个峰值是由第4个马赫波产生的。测点20第1个峰值是由首个马赫波产生的，第2、第3和第4个峰值分别是由地面初次反射波、第3个马赫波和第4个马赫波产生的。

总之，与在近地空爆情况下特定位置仅承受一次马赫波或入射波和反射波作用不同，在扁平大空间地面处发生爆炸的情况下，特定位置既要承受首个马赫波或初始入射波和顶板初次反射波作用，还要承受来自地面和顶板的多次反射波，以及沿着顶板或地面快速传播的其他后续马赫波作用。由于后续马赫波的作用范围始终较小，因此，承受后续马赫波作用的位置基本在地面和顶板处，或距离地面和顶板很近的位置。同时，后续马赫波的传播速率均较首个马赫波大，因此，后续马赫波最终都追上首个马赫波，并与其交汇，在交汇处的压力较首个马赫波其他位置要大。后续马赫波出现的位置在地面和顶板间交替出现，随着距离爆源越来越远，强度逐渐减弱。

3 最大峰值超压分析

在8 种爆炸TNT 当量情况下，距离地面5 种高度处最大峰值超压随距离爆源水平距离的变化关系如图5 所示。可见，距离地面各种高度处的最大峰值超压均随着距离爆源水平距离的增加而减小，且减小幅度逐渐降低；当水平位置相同时，5 种高度处最大峰值超压值的差异因距离爆源水平距离远近的不同而不同，距离爆源越近差异越大，距离爆源越远差异越小，直至几乎相同。爆炸TNT 当量越小，竖向5个最大峰值超压值趋于相同时所对应的水平距离越大。根据第2 节分析可知，竖向最大峰值超压差异的逐渐变小反映了后续马赫波对首个马赫波影响程度的逐渐降低。对于特定的爆炸TNT当量，存在着某个水平位置临界点，在该位置及其外侧区域任意水平位置处马赫波阵面最大峰值超压恒定。

图5 最大峰值超压随距爆源水平距离的变化Fig.5 Relationship between maximum peak overpressure and horizontal distance from explosion source

为了确定竖向各测点最大峰值超压相同时所对应的平面位置以及最大峰值超压值，取竖向各测点所记录最大峰值超压值的最大和最小者的相对误差不大于5%作为马赫波阵面在此位置峰值超压是否恒定的判据，初步判断各工况马赫波阵面峰值超压恒定的位置。然后，在该位置附近加密测点，比较精确地确定各工况马赫波阵面峰值超压恒定的临界点位置。临界点平面比例爆距ZS和临界点最大峰值超压值PM随比例净高ZH的变化关系如图6 所示。ZS和ZH的表达式分别为

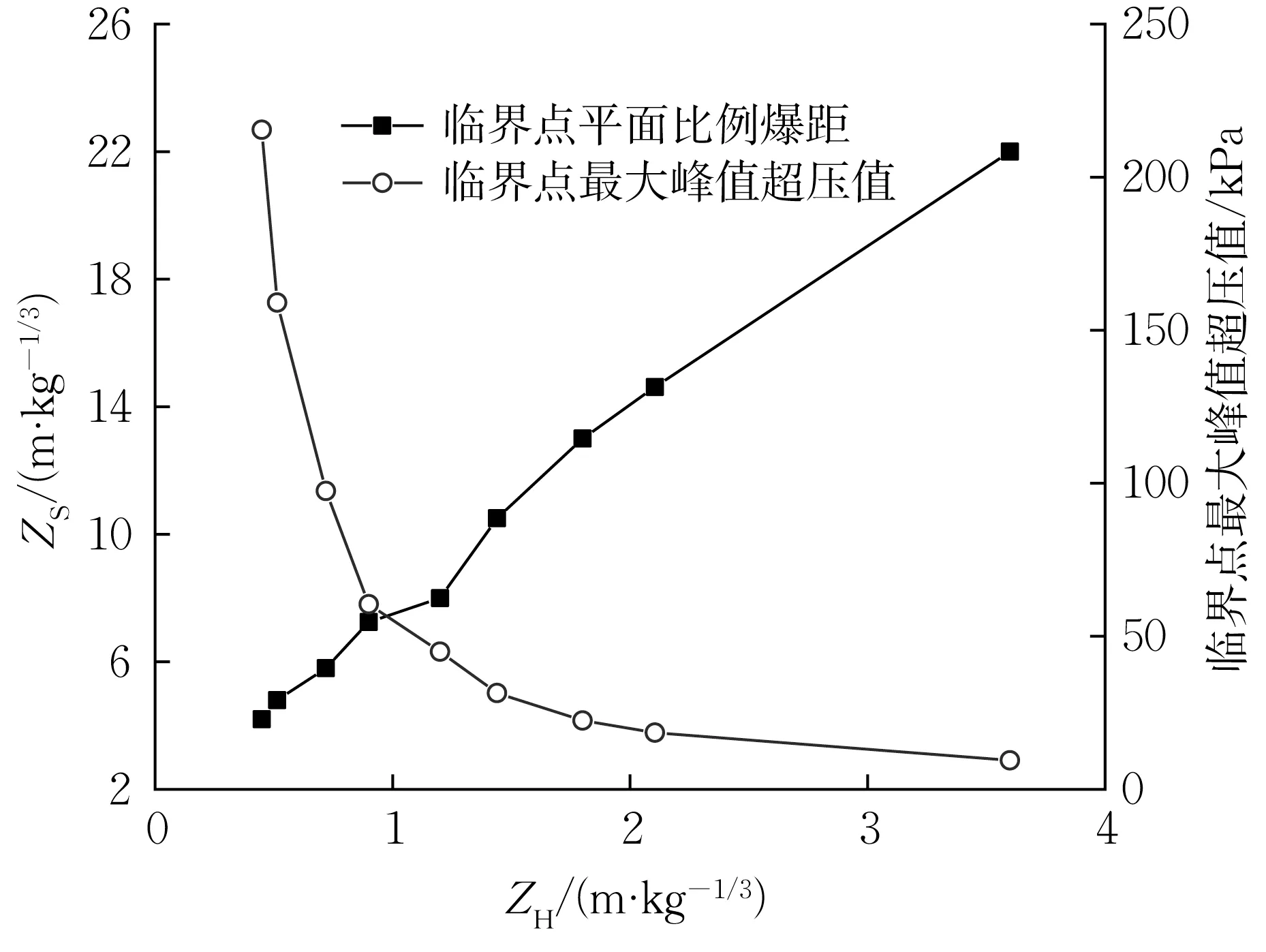
图6 马赫波阵面最大峰值超压恒定临界位置和对应值Fig.6 Constant critical position and corresponding value of maximum peak overpressure of Mach wave

式中：S为某位置与爆源之间的水平距离，m；W为爆炸TNT当量，kg。

由图6 可见，比例净高ZH越大即在相同净高条件下爆炸TNT当量越小，临界点平面比例爆距ZS越大；临界点最大峰值超压值随比例净高的增加呈指数形式衰减。对比分析各工况临界点和临界点外的最大峰值超压发现，临界点外与临界点处的最大峰值超压相对误差均在10%以内，即自临界点向外最大峰值超压值衰减缓慢，这一特点与爆炸冲击波在等截面矩形隧道内的传播情况相同［34］。

利用最小二乘法对图6 数据进行拟合，得到马赫波阵面峰值超压恒定时平面比例爆距ZS和临界点最大峰值超压值PM的计算式为

二者的相关系数R2分别为0.991 6和0.997 8。

利用式（3）—（6）可以根据爆炸TNT 当量和空间净高快速确定马赫波阵面峰值超压恒定的临界点位置以及该位置处的最大峰值超压值。同时，也可以根据空间净高和临界点距离爆源的水平距离S或临界点处的最大峰值超压值确定爆源处的爆炸TNT当量。

由于爆炸冲击波在扁平大空间内传播时会在地面和顶面之间多次反射，导致同一平面位置竖向各点的最大峰值超压不尽相同，为较合理地描述最大峰值超压在平面的分布情况，可以采用竖向各点最大峰值超压的平均值来表示。各工况竖向最大峰值超压平均值随平面比例爆距ZS的变化关系如图7所示。

图7 竖向最大峰值超压平均值随比例爆距的变化Fig.7 Relationship between average vertical maximum peak overpressure value and scaled distance

利用最小二乘法对图7 数据进行拟合，得到任意平面位置竖向最大峰值超压平均值的计算式如式（7）：

式中：a、b和c的取值如表3所示。应用该式，并结合文献［35-37］给出的人体伤亡超压阈值，可以快速确定特定爆炸工况下人体伤亡的分布区域。

表3 拟合公式系数和相关系数Tab.3 Fitting formula coefficients and correlationcoefficients R2

4 结论

采用AUTODYN 软件分析了爆炸冲击波在地下停车场等扁平大空间内的传播规律，主要结论如下：

（1）与在近地空爆情况下特定位置仅承受一次马赫波或入射波和反射波作用不同，在扁平大空间地面处发生爆炸的情况下，特定位置既要承受首个马赫波或初始入射波和顶板初次反射波作用，还要承受来自地面和顶板的多次反射波以及沿着顶板或地面快速传播的其他后续马赫波作用。后续马赫波的马赫杆高度均较低，但传播速率均较大于马赫波，最终都会追上首个马赫波，并与其交汇，在交汇处的压力较首个马赫波其他位置要大。后续马赫波出现的位置在地面和顶板间交替出现，且距离爆源越来越远，强度越来越弱。

（2）距离地面各种高度处的最大峰值超压均随着距离爆源水平距离的增加而减小，且减小幅度逐渐降低；同一水平位置竖向各点最大峰值超压值的差异因距离爆源水平距离远近的不同而不同，距离越近差异越大，距离越远差异越小，直至几乎相同。竖向最大峰值超压差异的逐渐变小反映了后续马赫波对首个马赫波影响程度的逐渐降低。

（3）存在着某个水平位置临界点，在该位置及其外侧区域任意水平位置处马赫波阵面最大峰值超压恒定，该位置对应的平面比例爆距随着比例净高的增加而线性增大，该位置的最大峰值超压随比例净高的增加呈指数形式减小。

（4）扁平大空间内任意水平位置处最大峰值超压平均值是比例净高和平面比例爆距的函数，当比例净高相同时，最大峰值超压平均值随平面比例爆距的增加呈指数形式减小。

作者贡献声明：

刘中辉：完成数值模拟、数据分析，撰写论文初稿。

匡志平：确定具体研究内容和实施方案，指导论文撰写及修改成稿。