采用超高性能混凝土和限位装置的斜拉桥易损性分析

郑 越， 王宇霄， 郭军军， 李方元

（同济大学 土木工程学院，上海 200092）

我国处于环太平洋地震带和亚欧地震带之间，大陆及周边地区里氏7 级（M 7）以上地震活动与全球地震大震活动有着准同步演化的特征，自2000年以来我国至少已经发生了2 次M 8级及以上地震和4 次M7 级及以上的地震。同期国外发生的较大地震有2011 年发生在环太平洋地震带的东日本大地震（M 9.0），造成了15 900 人死亡和252 人失踪；2015年发生在印度板块与亚欧地震带接壤的尼泊尔大地震（M 8.1），死亡人数超过8 000人，直接经济损失超过650亿人民币；土耳其在2023年2月6日发生了历史上罕见的震群型地震，包括了2次M7.8级的大地震，造成了巨大人员伤亡和财产损失。以上种种迹象表明：全球进入了与20世纪前半叶类似的处于大地震多发的状态。虽然地震中因桥梁破坏直接造成大量人员伤亡的情况并不多见，但因为桥梁破坏导致交通中断而间接造成的人员与经济损失巨大，因此，应当对桥梁的抗震性能的韧性提升加以足够重视。斜拉桥的震害主要表现为：主梁位移过大引起梁体之间或梁体与桥台之间的碰撞、主塔或边墩塑性铰区的损伤以及斜拉索的断裂等。因此，提高斜拉桥整体结构体系的抗震能力需要提升其易损构件的抗震韧性。

众所周知，现有的抗震设计主要包括延性抗震设计和减、隔震设计2种方法［1］。延性设计方法是在满足“能力保护”思想的前提下通过选定结构某些部位使其地震作用下产生塑性铰，充分利用结构或构件的塑性变形耗散能量的同时延长结构的自振周期降低地震力以达到抗震的目的；减、隔震技术是利用减震或隔震装置使装置进入塑性产生较大阻尼或者延长结构的自振周期以阻止地震能量传递到主体结构中，从而达到减震效果［2］。然而，延性抗震的设计是以牺牲部分结构构件而保证结构整体性能的设计方法，由于结构构件产生了塑性破坏，震后修复可能变得极为困难，需要投入的时间和经济成本较大，因此在应用上存在一定弊端。随着减、隔震技术的不断更新发展，涌现出了各种减、隔震装置，这些装置成本相对较低、易于更换，且不影响主体结构的使用，因此在桥梁工程中得到了广泛的应用。形状记忆合金（SMA）具有良好的超弹性和形状记忆功能，其在抗震中表现出的良好韧性得到了越来越多的关注［3-8］，作为减震装置的优选材料有较大的应用前景。但目前SMA材料还较少应用于实际工程中，尤其是像在斜拉桥这样的大跨度桥梁中，目前的减震装置往往仅能在单一方向上发挥作用，无法在多方向上同时起到减震的作用。超高性能混凝土（UHPC）是近些年来快速发展的新型建材，它具有优异的抗压强度（大于120 MPa）、抗拉强度（大于10 MPa）以及抗拉应变强化特性，弹性模量也比普通混凝土高出约50%，目前主要应用于正交异性钢桥面铺装［9］、钢混组合连续梁桥的负弯矩区以及桥梁的湿接缝等领域。但它在大跨度斜拉桥塔中的应用还不多见。因此，为了提高大跨度斜拉桥的抗震韧性，提出一种韧性提升的技术：一方面将UHPC 材料应用于塔柱的塑性铰区，另一方面将SMA拉索限位装置安装于主梁与桥塔之间用来限制地震时梁体可能发生的过大位移。随后经过易损性的分析发现，该技术不仅能使斜拉桥在地震作用时塔柱始终保持弹性受力状态，还能使主梁的位移满足规范要求，大大提高斜桥梁的抗震韧性。

1 材料与限位装置的本构关系模型

1.1 超高性能混凝土材料

为了将UHPC 材料应用于桥梁抗震领域，就需要用到其本构关系模型，根据已有的研究成果，UHPC本构关系模型（如图1所示）主要包括受压区和受拉区。其中受压区的骨架线为OJP，受拉区的骨架线为OAFI，可以发现受拉段包含了应变强度段AF，这是UHPC的材料性能相比一般混凝土的最大优势之一。UHPC材料的本构关系模型在受拉和受压区加载和卸载时的滞回准则分别如图2a 和2b所示。

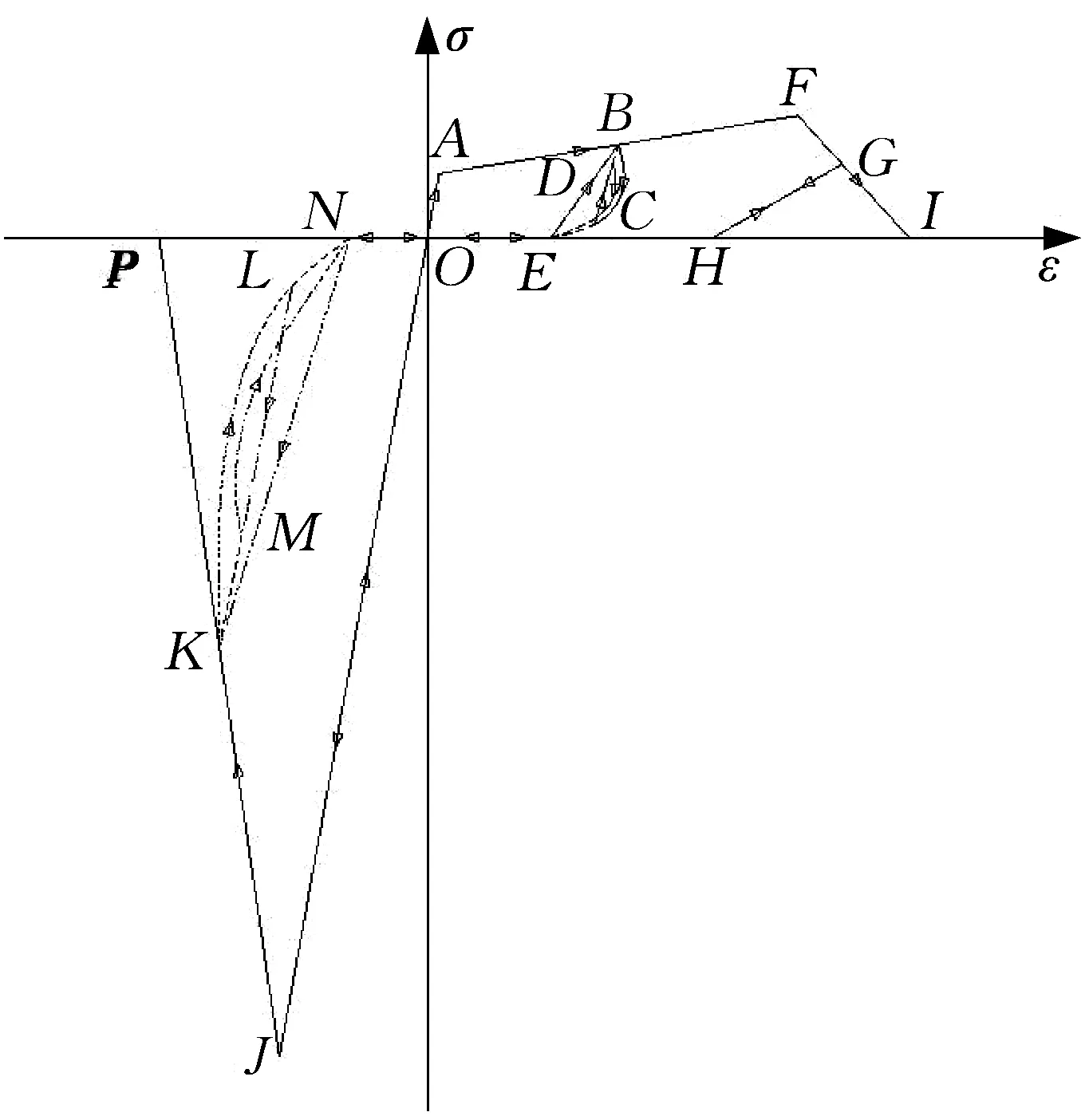
图1 超高性能混凝土材料本构关系模型Fig.1 Constitutive model of UHPC material

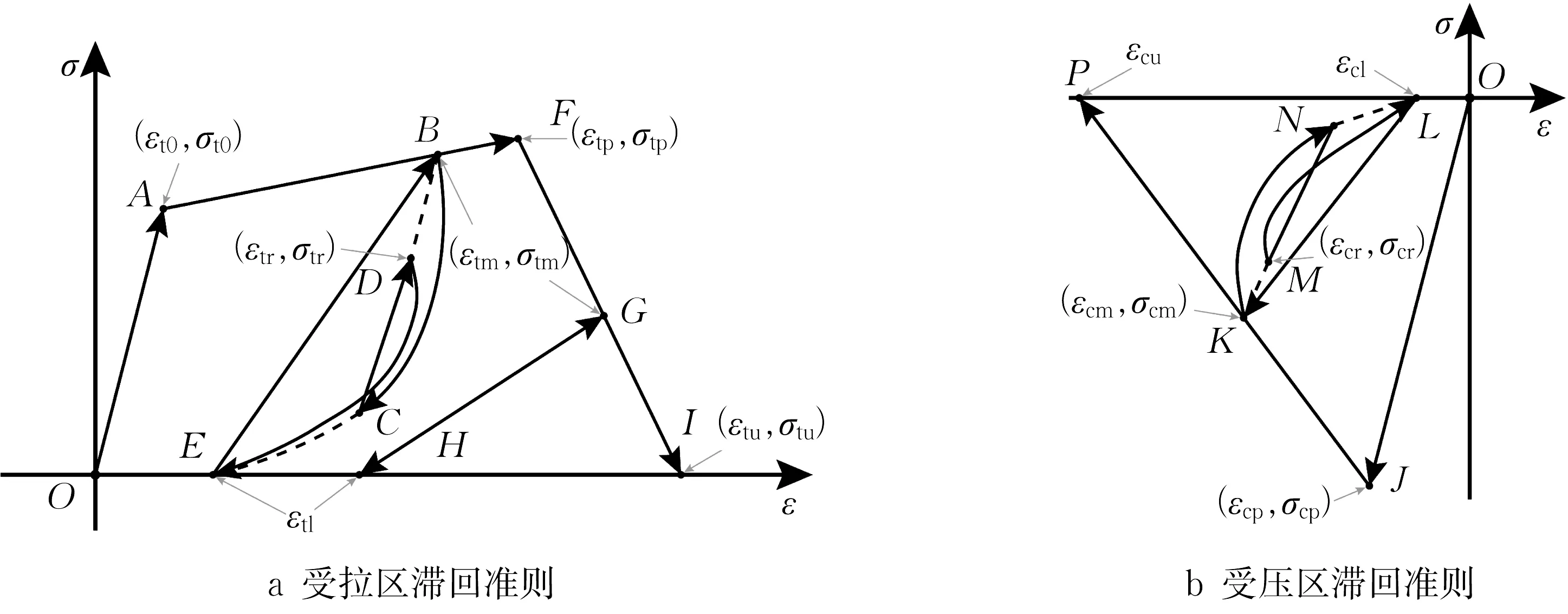
图2 超高性能混凝土材料的滞回准则Fig.2 Hysteretic rules of UHPC material

受拉区骨架线OAFI主要有四部分组成，如式（1）—（4）所示：

式中：σtensile为材料所受拉应力；E为弹性模量；σt0为开裂应力，当UHPC 材料的应变ε大于开裂应变εt0时表示材料开裂；σtp为材料最大的抗拉强化应力；εtp为材料最大的抗拉强化应变；εtu为拉应力在骨架线上降为零的应变，一旦应变大于εtu则应力均为零。

受压区段骨架线OJP主要由三部分组成，如式（5）—（7）所示：

式中：σcompressive为材料所受压应力；σcp为最大压应力；εcp为最大压应力时的受压应变；εcu为压应力在骨架线上降为零的应变，一旦应变大于εcu则应力均为零。

在受拉区范围内UHPC材料加载和卸载时的滞回准则如式（8）—（11）所示：

式中：αt为一个大于1.0的常数，具体值由试验确定；εt0和εtp分别为A和点F的应变。

曲线段BCE代表受拉区的初次卸载段，其具体表达式见式（9），当ε'cm≥εcm时，有

式中：εtm为第1 次受拉区卸载时在骨架线上到达过的最大应变；σtm为对应应力；εtprl为卸载后部分重加载到达的最大应变。σ'tm代表ε'tm对应应力，εtl为初次卸载时应力为零的应变（例如点E和H对应的应变），εtl=βt·εtm，其中βt为一常数。

直线段CD代表一个典型的局部再加载准则，其表达式参见式（10），CD的延长线要确保与历史上曾经到达过的最大应变点B相交，其中ε'tl值定义为

式中：εtpul为卸载时的最小应变；σ'tl为ε'tl对应应力；εtr和εtu分别为点D和点I的应变。当在骨架线上超过点F（例如：FG）时的卸载和再加载路径则由式（11）给出。

在受压区范围内UHPC材料加载和卸载时的滞回准则为

式中：αc为一个大于1.0的常数，具体值由试验确定；εcp和εcu分别为J和点P的应变。

图2 所示的受压区直线段KN的应变由式（13）给出，当ε'cm≥εcm时，有

式中：εcm为受压区骨架线上卸载时的应变（例如点K的应变）；σcm为对应应力；εcprl为卸载后部分重加载时的最小应变（负应变）；σ'cm为ε'cm对应应力；εcl为初次卸载时应力为零时的应变（例如点L的应变），εcl=βc·εcm，其中βc是一个常数。

受压区直线段NM由式（14）给出，其中ε'cl值为

式中：εcpul为卸载后部分重加载到达的最小应变（负 应 变）；σ'cl为ε'cl对 应 应 力；εcr为 点M的应变。

1.2 形状记忆合金拉索耗能限位装置

SMA 拉索耗能限位装置由上滑槽、下滑槽、上销轴、下销轴、钢挡板、SMA 拉索和引导板组成。装置上滑槽为一槽型钢，在一端处设置一个凹槽，在凹槽底板上打孔穿过上销轴。下滑槽也为槽型钢，尺寸略大于上滑槽，确保上滑槽能够插进下滑槽中，下滑槽一端设置一个与上滑槽相同的凹槽，凹槽底板打孔，下销轴穿过孔洞与下部结构相连。上下滑槽端部凹槽分别位于装置两端，凹槽底板处于同一水平面上，保证两端受力在同一直线上以避免产生力矩导致装置发生倾覆。2 块矩形钢挡板设置在装置两端，在钢挡板上开若干数量的孔洞，SMA 拉索穿过两侧钢挡板上的孔洞，通过螺母锚固。引导板可选用角钢，装饰每端2 块引导板焊接在下滑槽上，保证钢挡板在水平方向运动而不发生其他方向上的移动和转动。装置的构件和组装如图3所示。

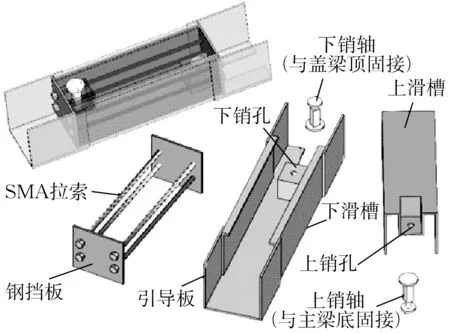
图3 形状记忆合金拉索耗能限位装置部件和组装Fig.3 Components and assembly of SMA-cable energy consumption and displacement constraint device

1.3 形状记忆合金耗能限位装置的本构关系模型

根据以往研究结果，SMA 单丝和SMA 拉索在循环加载下均会呈现“旗帜”形滞回曲线，但SMA单丝和拉索在循环荷载作用下又有2 点不同：① 单丝的弹性阶段的屈服应力大于拉索；② 单丝的屈服前刚度则小于拉索。综合考虑SMA 拉索和耗能限位装置的特点，在OpenSeesPy 软件中采用ASD_SMA_3K、MinMax 和ElasticPPGap 材料进行组合，再现SMA 材料的超弹性、强度退化效应、残余应变累积效应和松弛效应，模拟出了SMA拉索耗能限位装置力（F）与位移（Δ）的本构关系模型，如图4所示，其中lgap为SMA拉索的松弛长度。

2 数值算例

2.1 工程背景

选取的斜拉桥主跨跨径为360 m，边跨设有辅助墩，两端为过渡墩，桥梁跨径组合为（61+87+360+87+61） m，桥型总体布置如图5a 所示。图5b 为主梁标准横断面图，采用钢主梁和混凝土桥面板的双肋式组合形式，主梁高度为3.2 m，宽度35.4 m。桥塔采用“A”字型桥塔，图5a中所示的A2和A3主塔高均为123.8 m，横梁以下塔高13.8 m，横梁以上高110 m，塔柱截面形式为4 m×6.5 m～6 m×9.0 m的箱型截面。斜拉索呈扇形布置，索的数量为112根，主梁上的标准索距为12 m，加密处索距为8 m。辅助墩采用双柱墩，墩高为21 m，过渡墩为框架墩，设有盖梁，墩高为13 m，辅助墩和边墩均采用5 m×3.5 m的圆端形箱型截面，桥墩构造及其关键截面如图5c所示。桥塔采用C50混凝土，边墩和承台等采用C40混凝土；桩基采用C30 混凝土。普通钢筋采用HRB335。

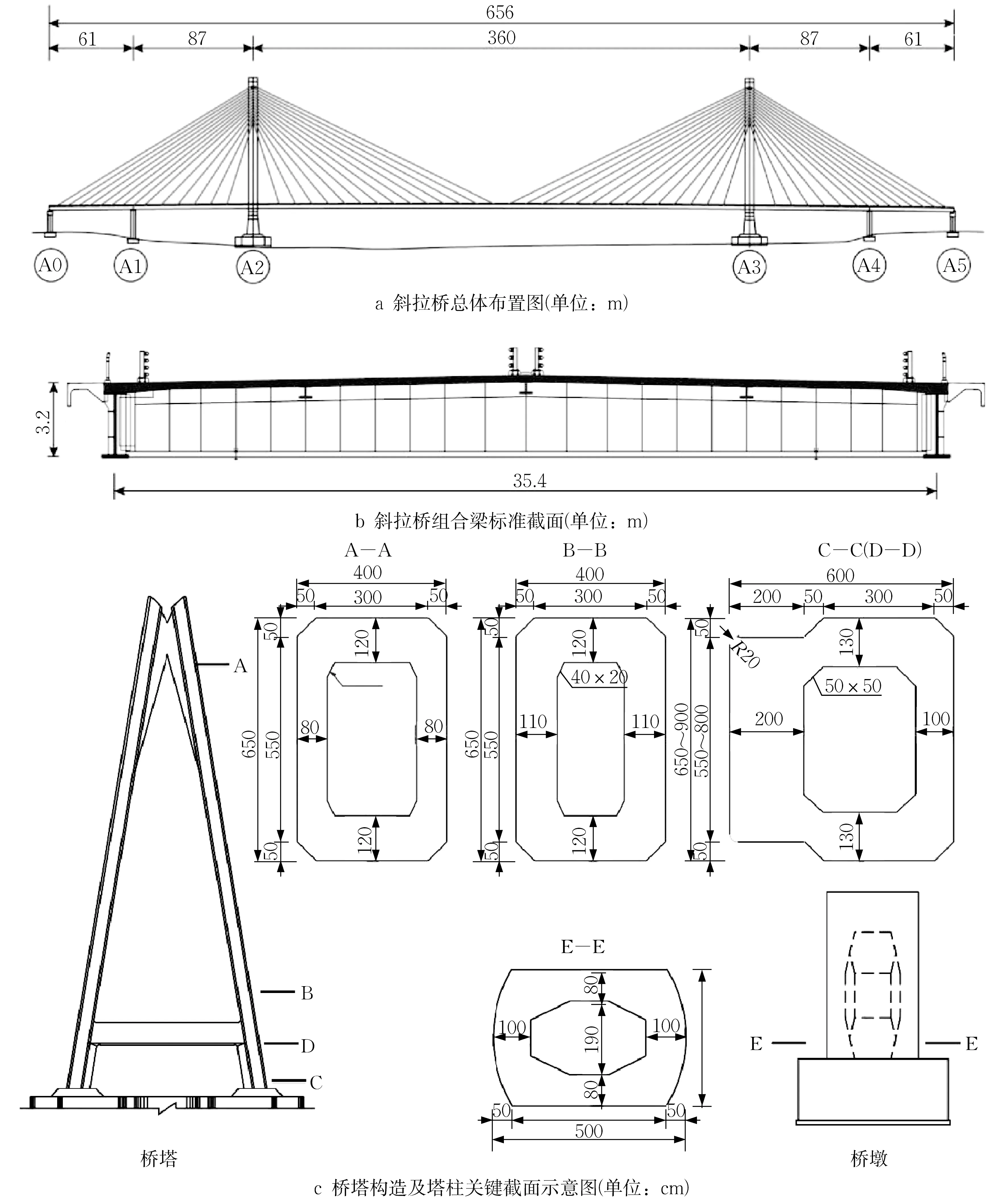
图5 斜拉桥构造Fig.5 Structure cable-stayed bridge

2.2 模型建立

在基于Python 的OpenSeesPy 平台中建立斜拉桥的有限元模型，其全桥模型如图6 所示。由于主梁刚度较大，在地震作用中不会进入塑性状态，因此采用空间弹性梁柱单元（elasticBeamColumn element）模拟，用与实际桥梁主梁质量相等的单梁代替。拉索采用桁架单元（truss element）模拟，拉索和主梁之间通过刚性单元（rigidLink）连接，通过施加初始应变保证桁架单元内力与成桥状态索力一致。球型钢支座采用零长单元（zeroLength element）模拟，将支座的刚度赋予零长单元即可。对于主塔和桥墩，在地震作用下可能会进入弹塑性状态，因此采用非线性梁柱单元（ForceBeamColumn element）进行模拟，将桥塔和桥墩离散为核心混凝土、保护层混凝土和钢筋纤维单元，如图7所示，纤维单元之间完全黏结且满足平截面假定，核心混凝土、保护层混凝土和钢筋纤维单元采用不同的本构关系模型，而桥塔横梁和过渡墩盖梁采用弹性梁柱单元（elasticBeamColumn element）模拟。使用m 法计算出桩基基础的刚度，通过赋予相应刚度的零长单元（zeroLength element）模拟桩基基础。

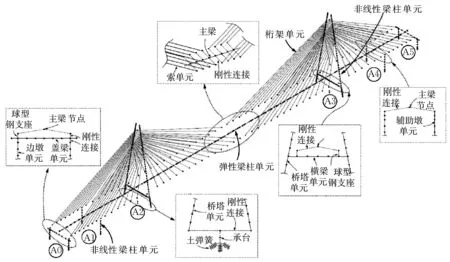
图6 斜拉桥有限元模型Fig.6 Finite element model of cable-stayed bridge

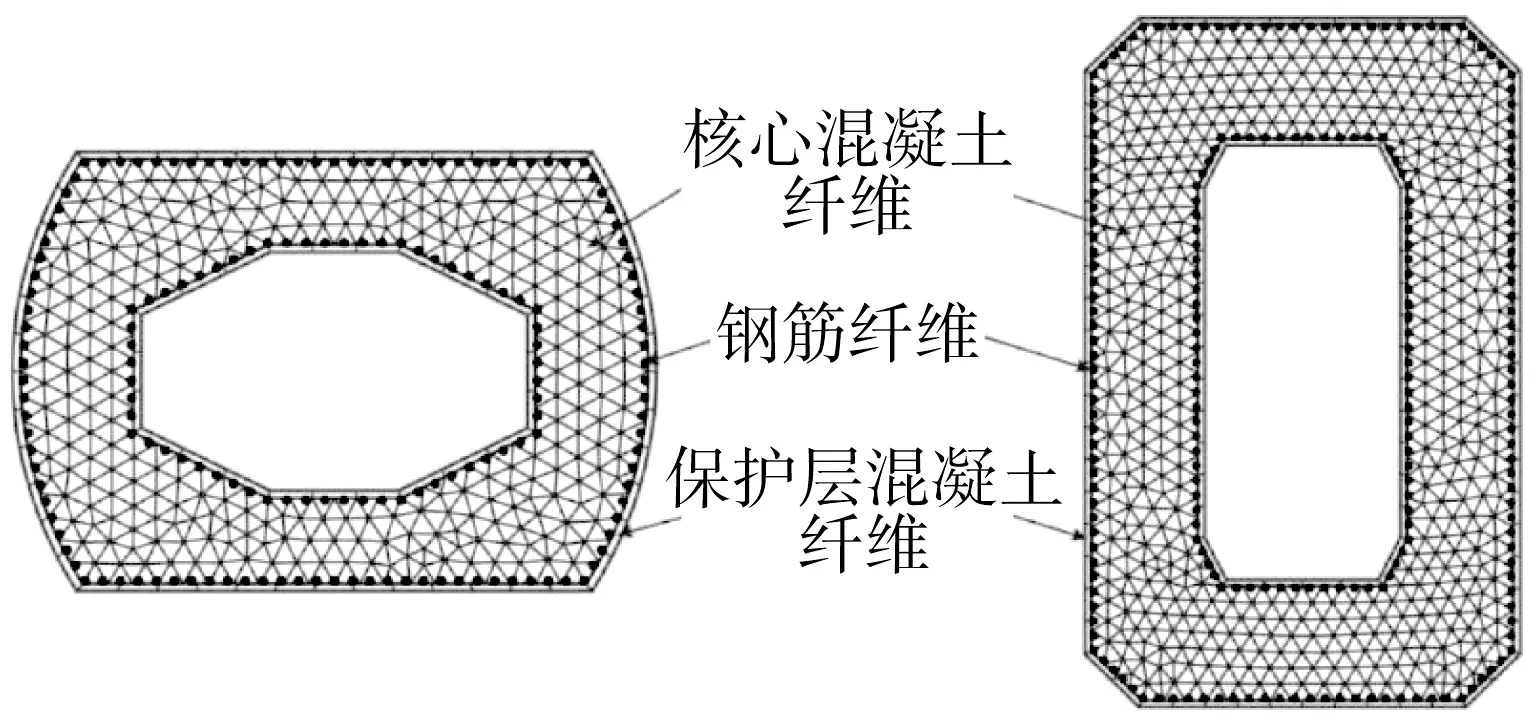
图7 桥塔及桥墩纤维截面示意Fig.7 Schematic diagram of fiber sections of bridge tower

2.3 SMA耗能限位装置的数值模拟

在斜拉桥模型中，采用零长单元（zeroLength element）模拟SMA 拉索减震耗能装置，零长单元（zeroLength element）的2 个节点坐标相同，装置两端节点与主梁和桥塔之间分别采用刚性连接（rigidLink），使主梁、桥塔分别与装置两端刚性连接。SMA 拉索的长度为5 m，等效面积和等效直径分别为0.038 5 m2和0.22 m。

2.4 材料参数

斜拉桥的桥塔主要采用C50 混凝土和HRB335型号的钢筋。易损部位采用UHPC 材料替换。UHPC材料的本构关系模型主要包括受压区和受拉区的多个参数，其中受压区的参数主要包括UHPC的抗压强度及其对应的应变，受拉区的参数主要包括开裂应力及应变、强化应力及应变等，上述材料各项参数的具体数值列于表1。

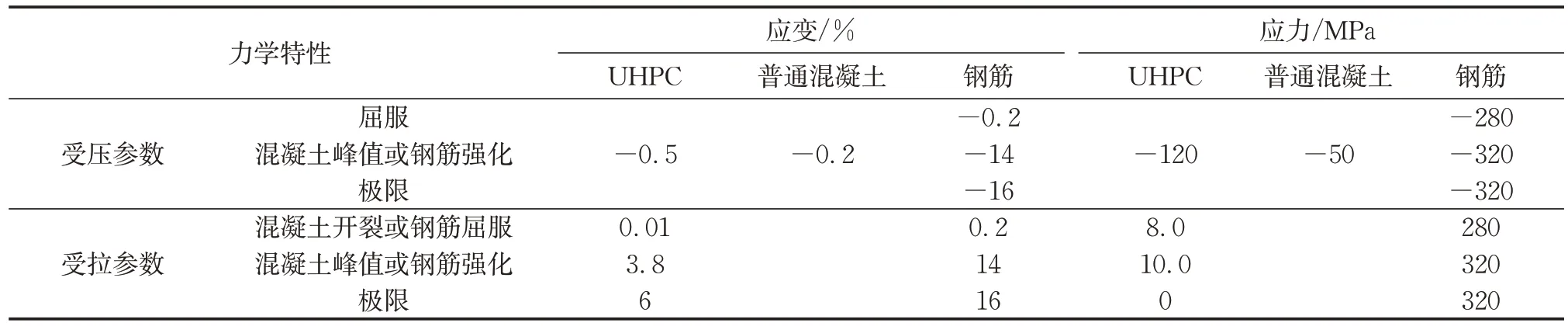
表1 材料参数Tab.1 Parameters of material

2.5 新型斜拉桥减、隔震体系结构动力特性

根据上述参数建立斜拉桥的有限元模型并对其进行动力特性的分析，计算得到前6 阶周期以及振型特点，结果见表2。借助Guo 等［10］开发的基于Python 编程的OpenSees 前后处理工具SAPBridge可将模型数据库与OpenSeesPy相连，以方便有限元模型的检查和计算结果的处理。在SAPBridge中显示的前6阶振型如图8所示。

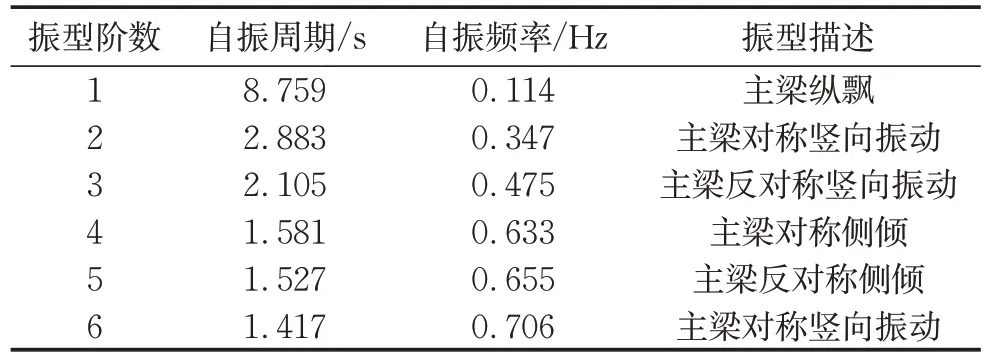
表2 斜拉桥动力特性Tab.2 Dynamic characteristics of cable-stayed bridge

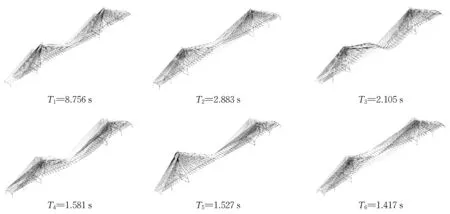
图8 斜拉桥模型动力特性Fig.8 Dynamic characteristic of cable-stayed bridge

3 易损性方法

3.1 概念

基于性能的地震工程全概率决策框架将结构的抗震性能分为四部分：地震危险性分析、结构地震响应分析、结构损伤分析和地震灾害损失评估［11］。近年来，基于抗震性能的结构分析框架愈发完善，地震易损性是其中的重要内容，地震易损性分析是指结构在承受不同强度的地震作用下发生不同程度破坏的可能性，也是结构达到或超过某一极限状态的超越概率［12］，它揭示了在给定地震动参数情况下，结构构件或体系达到或超越特定损伤状态阈值的概率，直观反应了地震作用下结构构件和体系发生损伤的可能性大小，为构件加固和损伤评估提供了有力依据。很多学者基于历史震害进行了易损性分析研究，不同学者建立易损性曲线的思路和方法也相差较大，其中根据理论生成易损性曲线的方法［13-15］能够兼顾材料、结构几何和地震动的不确定性，且有较低的成本投入和较高的可靠性，成为计算易损性曲线的主流方法，广泛应用于各种结构易损性分析。

3.2 分析方法

理论易损性曲线计算方法最开始为以反应谱为基础的弹性谱方法，逐步发展到以非线性静力分析为基础的非线性静力方法，随着计算机技术的飞速发展和易损性理论研究不断深入，现阶段的计算方法为以非线性时程动力分析为基础的云图法、增量动力分析（IDA）方法和贝叶斯方法。本文采用云图法。云图法选取真实存在的地震动记录输入，概念明确且计算简单，适用性强且可靠度高。云图法建立地震易损性曲线的基本内容有：选取地震动时程、选择合适的地震动强度指标和工程参数需求参数、建立概率地震需求模型、定义不同构件的损伤状态、生成构件易损性曲线和体系易损性曲线。

3.2.1 概率地震需求模型建立

首先建立概率地震需求模型（PSDM），假设工程需求参数EDP（Engineering Demand Parameter）的均值SD与地震动强度指标IM之间满足式（15）的关系：

式中：a和b均为回归系数。由此得到式（16）的概率地震需求模型为

式中：D为构件的位移与曲率等工程需求；Φ(·)为标准正态分布函数；βD为构件需求的对数标准差，如式（17）：

若进一步假定，构件在某一损伤极限状态LS j的能力C服从均值（SC）、对数标准差（βC）的对数正态分布，则云图法得到的构件在LSj下失效概率满足

其中βC为

式中：Cv为构件能力的变异系数。

由此可获得概率地震需求模型，如图9所示。

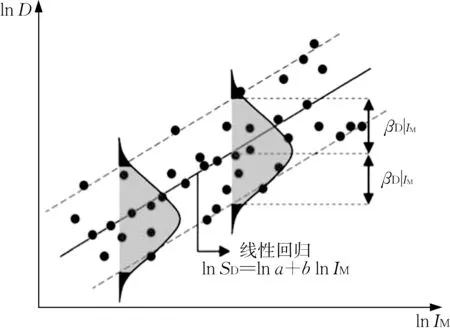
图9 概率地震需求模型Fig.9 Model of probabilistic seismic demand

式（15）中系数a和b通常通过普通最小二乘法计算得到。云图法采用最小二乘线性回归，因此也应满足最小二乘线性回归的4 个基本假设：① 自变量和因变量存在显著线性相关关系；② 残差服从正态分布；③ 残差的方差恒定；④ 不同残差之间相互独立。

3.2.2 地震动强度指标选取

合理的地震动强度指标对于易损性分析至关重要，需要建立的易损性曲线能够反映结构构件和体系的损伤概率随地震动强度指标变化的关系。郭军军［16］基于Box-Cox 变化与贝叶斯推断，计算了20 个地震动强度指标，包括幅值、频率和持时相关的指标的合理性，结果显示峰值速度（PGV）作为大跨度斜拉桥的地震动强度指标较为合适。Zhong 等［17-18］研究了远场及近场地震动激励下大跨度斜拉桥的合理地震动指标，研究结果表明PGV是斜拉桥的最优地震动指标。因此，根据上述研究，本文研究对象斜拉桥属于长周期结构因此宜采用PGV 作为地震动强度指标来计算结构易损性。

3.2.3 易损构件和指标选取

斜拉桥主要由主梁、拉索、主塔和桥墩组成。以往地震作用下斜拉桥各个构件的内力和位移分析结果表明，主梁在地震作用下一般保持弹性，不会发生材料的塑性破坏，因此，主梁损伤概率很低，为非易损构件；而参考Zhong 等［18］对斜拉桥易损性做出的划分，桥塔和斜拉索属于主要易损构件，支座属于次要易损构件。

桥梁主塔和桥墩是抗震研究中重点关注的对象，它们不仅能将上部结构荷载传递到基础，还起到抵抗整个体系在荷载作用下所产生的不平衡力。在罕遇地震作用下，主塔和桥墩的关键截面可能会进入材料塑性损伤阶段，当抗力不足时，甚至会发生倒塌的风险。为客观描述结构和构件的易损性，需借助损伤指标确定结构和构件的损伤状态。Hwang等［19］将桥梁结构损伤状态分为轻微损伤、中等损伤、严重损伤和完全损伤。本文参考Feng 等［20］提出的一种较为合理的截面损伤状态定义方法，当外层钢筋首次达到屈服时为轻微损伤的临界点，混凝土达到极限压应变时为完全损伤的临界点，将轻微损伤的临界点和完全损伤的临界点之间的区间三等分，可求得中等损伤和严重损伤的临界点。地震作用下斜拉桥索的损伤状态可以采用索力比划分，其定义为地震作用下斜拉索索力与恒载作用下斜拉桥的索力的比值，斜拉索的损伤状态阈值的定义可以参考以上定义桥墩和桥塔的方法，当索力到达极限承载力，索力比为完全损伤状态阈值，成桥状态索力比与极限承载力索力比之间四等分点分别定义为轻微损伤状态阈值、中等损伤状态阈值、严重损伤状态阈值。本文研究的斜拉桥使用球型钢支座，根据地震作用下支座产生的剪切位移大小定义支座的4种损伤状态阈值。根据《公路桥梁球型支座规格体系》［21］中列出的支座容许最大位移定义为轻微损伤状态，支座顶板边缘与聚四氟乙烯板另一端的距离定义为完全损伤状态，将两者阈值之间的2 个三等分点分别定义为中等损伤状态阈值和严重损伤状态阈值。

3.2.4 体系易损性计算

结构体系的易损性往往高于结构构件的易损性，所以，应该在构件易损性基础上进行体系层面的易损性计算。目前最常见的方法是一阶界限法，该方法通过一阶可靠度的理论分析，基于结构构件的易损性分析，计算出桥梁结构体系的易损性。体系易损性的下界为假设各个构件并联时的损伤概率，即认为最后一个构件进入损伤状态时整个结构体系进入损伤状态，计算结果偏于危险；体系易损性的上界为假定各个构件串联，即认为第1 个构件进入损伤状态则整个结构体系进入损伤状态，计算结果偏于保守。通过一阶界限法可以得到体系的易损性的范围，实际的易损性介于上界和下界之间，无法得到精确的易损性曲线。对于含有多个EDP的情形，要得到体系的易损性曲线，必须计算多维概率密度函数，通常情况下难以得到解析解。Nielson 等［22］提出采用数值计算的方法，结合蒙特卡洛抽样模拟，计算出体系较为精确的易损性曲线。首先计算协方差矩阵，若需求数量为n，地震动数量为m，因此得到一个m行n列的矩阵，矩阵中每个元素的值为每个工程需求参数的自然对数值，计算得到矩阵的协方差矩阵，然后再进行蒙特卡洛抽样，在计算体系易损性时分别对能力和需求进行抽样，得到需求值和能力值，进而给出结构体系的易损性曲线。

每一次随机抽样的结果可以表示为式（20）：

式中：x1，x2，…，xn分别为n个构件X1，X2，…，Xn考虑相关性后的抽样值；F1∪F2∪…∪Fn为联合分布函数的失效域；Fi为单个构件的失效域。由此，在某一特定损伤状态下(DS)，特定强度水平(IM=IMi)下体系的失效概率可表示为式（21）：

式中：N为随机抽样次数。进行100 000次随机抽样得到需求值和能力值，最终拟合出体系的易损性曲线。

4 易损性分析

4.4 形状记忆合金体系易损性曲线

根据太平洋地震工程研究中心（PEER）的已发地震记录信息选取86 条地震波，其PGV 涵盖从了15.4 cm·s-1至200.8 cm·s-1的范围。根据上述地震波计算出斜拉桥纵向的地震动响应，从而得到各个构件易损性计算的需求数据峰值，再结合桥梁本身的能力均值，可计算出各个构件的易损性曲线，进而可拟合出体系的易损性曲线。

4.4.1 构件易损性曲线

图10 为边墩、辅助墩和主塔支座的易损性曲线。如图所示，边墩支座相对于辅助墩和主塔的支座进入各个损伤状态较早，这是由于边墩支座承受的竖向力较小，所采用的尺寸和型号较小，各损伤状态的临界值较低且接近，因此边墩支座相对于主塔和辅助墩支座更容易发生破坏。当PGV 大于150 cm·s-1时，边墩支座有超过75%的概率会完全损伤，因此在该结构下是极易损构件。主塔支座采用的尺寸和型号较大，相较于边墩支座和辅助墩支座很难发生破坏，即使PGV达到200 cm·s-1，主塔支座完全损伤的概率只为27.9%。

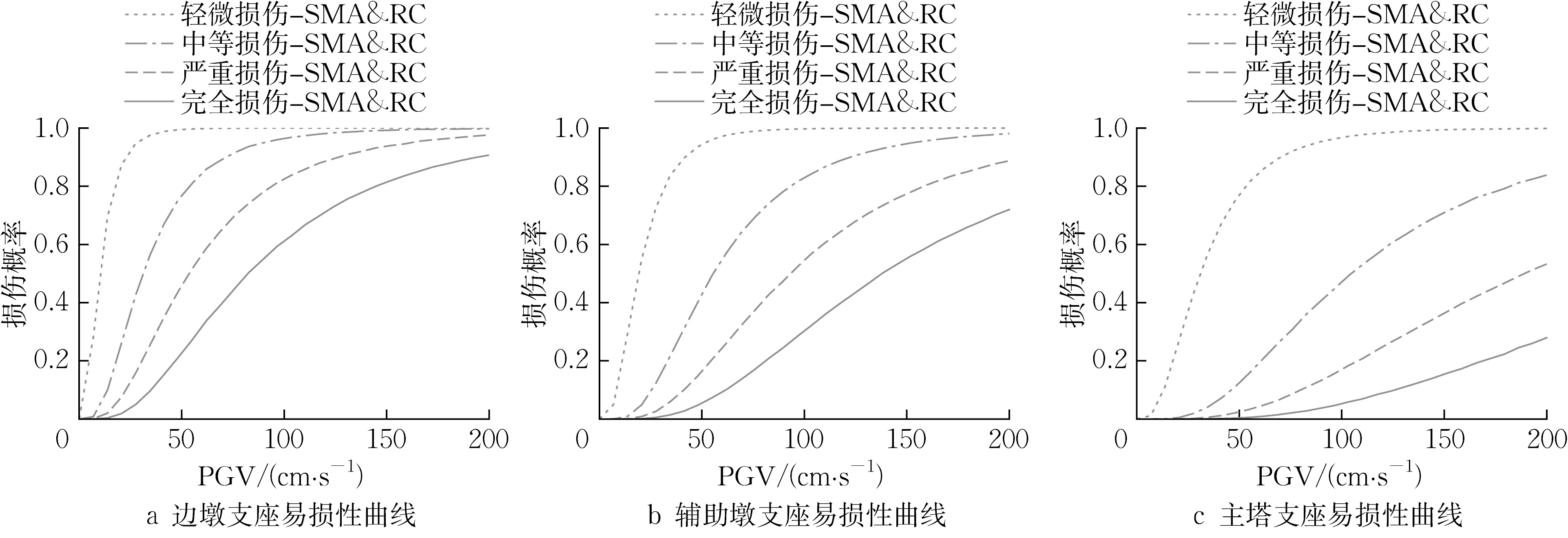
图10 形状记忆合金体系支座易损性曲线Fig.10 Bearing fragility curves of the SMA system

图11为斜拉桥辅助墩处拉索、中跨主塔处拉索和边跨主塔处拉索的易损性曲线。如图所示，在地震作用下，辅助墩处拉索和中跨主塔处拉索以轻微损伤为主，即使PGV达到200 cm·s-1，辅助墩处拉索中等损伤的概率只有5.5%，中跨主塔处拉索中等损伤的概率仅18.5%，辅助墩处拉索中等损伤的概率约为5.0%。而边跨主塔处拉索的损伤概率变化较为明显，当PGV达到150 cm·s-1时，边跨主塔处拉索中等损伤的概率超过90%，当PGV 达到200 cm·s-1时，边跨主塔处拉索严重损伤的概率达到81.1%，完全损伤的概率为41.0%。由此可见斜拉索的易损性与其所在位置有很强的关联性，在本文中，边跨主塔处拉索是典型的易损构件，而辅助墩处拉索和中跨主塔处拉索不是易损构件。

主塔的关键截面易损性曲线如图12 所示。从图中可以看出，主塔A—A 截面在PGV 较大时以发生轻微损伤为主，当PGV 达到200 cm·s-1时发生中等损伤的概率为6.2%且几乎不发生严重损伤；B—B截面和D—D截面分别处于斜塔横梁的上下侧，为桥塔较薄弱截面，当PGV达到50 cm·s-1时出现轻微损伤的概率均超过95%，PGV较大时还有概率发生中等损伤，且有较小概率发生严重损伤，但完全损伤可不考虑。对于塔底部C—C截面，在地震作用下出现损伤的概率非常大，当PGV 达到200 cm·s-1中等损伤的概率为94.1%，严重损伤的概率为69.2%，完全损伤的概率也达到了35.2%，必须加固提高。

4.4.2 结构易损性曲线

在考虑体系易损性曲线时，即使支座在达到严重损伤甚至完全损伤，整体结构也不会倒塌失去桥梁本身的功能，且震后更换修复支座也较为容易，因此，在计算体系易损性曲线时可仅考虑支座的轻微损伤和中等损伤，不定义支座的严重损伤和完全损伤。

经计算后体系的易损性曲线如图13 所示。在安装了SMA 拉索减震限位装置后，当PGV 达到100 cm·s-1时，从轻微损伤到完全损伤的概率分别为100.0%、95.8%、45.9%、20.6%，而当PGV 达到200 cm·s-1时，其概率分别为100.0%、99.8%、85.2%、62.1%。体系的易损性曲线显示出斜拉桥在地震作用尤其是强震作用下仍然大概率会面临构件失效、失去承载力甚至倒塌的风险，风险源主要来自边跨桥塔处拉索的损伤以及桥塔的3处薄弱截面（B—B 截面、C—C 截面、D—D 截面）尤其是C—C截面的损伤。因此有必要通过加固桥塔的措施降低桥塔薄弱截面的损伤概率，进而控制和降低桥梁体系失效或倒塌的风险。

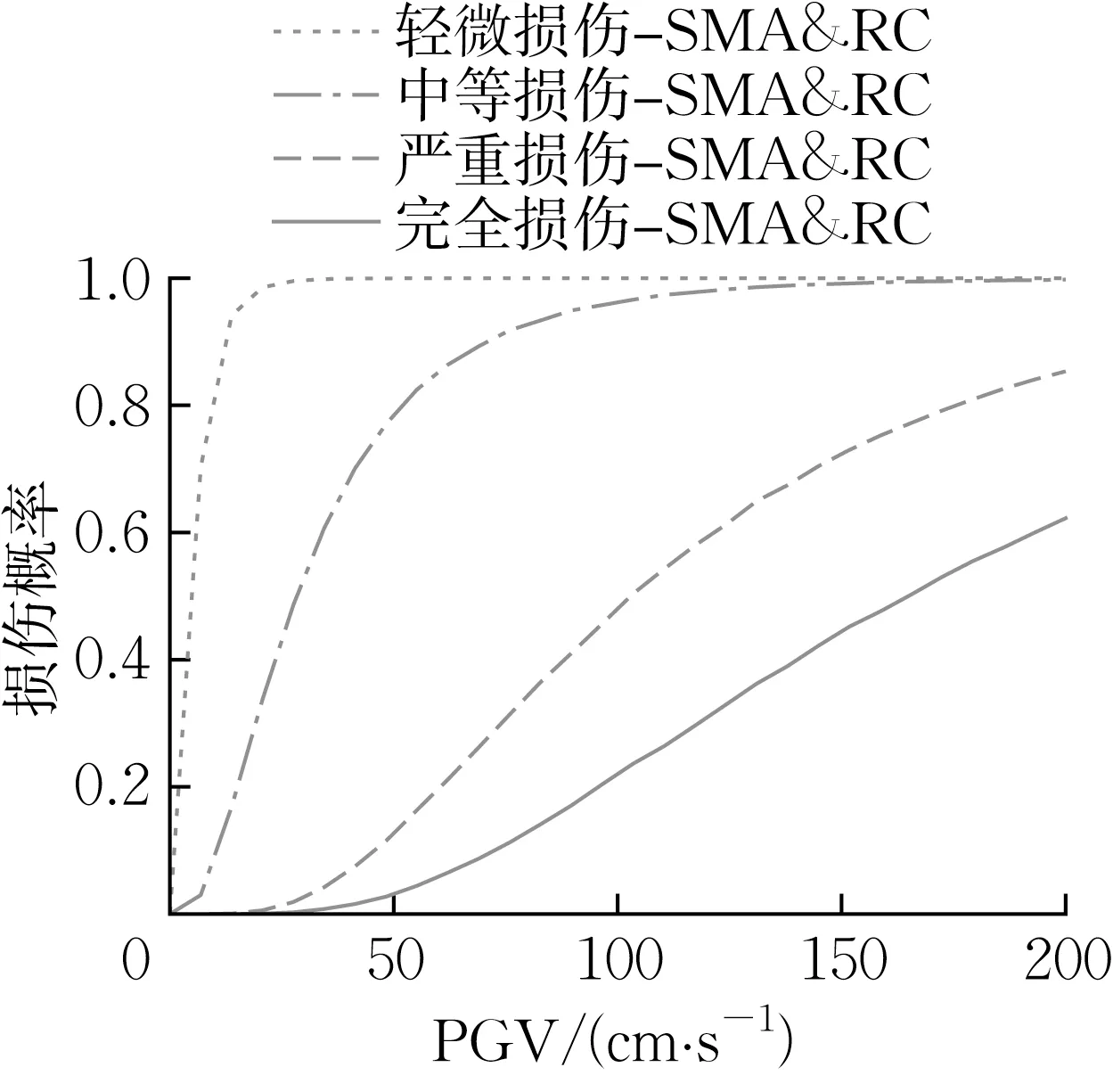
图13 斜拉桥形状记忆合金体系易损性曲线Fig.13 SMA system fragility curves of the cablestayed bridge

4.5 超高性能混凝土材料的韧性提升

将主塔最下端44.8 m 范围内的C50 材料更换为UHPC材料，涵盖了B—B、C—C、D—D截面并向上延伸，避免该区域太小导致地震作用下C50 和UHPC材料交界面弯矩过大形成新的薄弱截面。

4.6 新型桥梁体系的易损性分析

在将桥塔下部普通C50混凝土替换为UHPC新材料后，采用相同的地震波计算斜拉桥纵向的地震动响应，使用前述的方法，可计算并对比2个结构体系下各构件的易损性差别，进而进一步比较体系的易损性差别。

4.6.1 构件易损性曲线

图14 为边墩、辅助墩和主塔支座的易损性曲线。可以看出，UHPC 的加固对支座的易损性曲线几乎没有影响，说明支座损伤对主塔刚度的变化不敏感，即在地震作用下主塔刚度的改变对支座易损性的影响较小。

图15为斜拉桥辅助墩处拉索、中跨桥塔处拉索和边跨桥塔处拉索的易损性曲线。可以看到两体系下斜拉索的易损性曲线差别不大，在PGV 达到200 cm·s-1时，除了辅助墩处拉索轻微损伤概率从73.5%下降到67.6%，其余2 处的拉索各自损伤概率都有小幅的升高，其中边跨桥塔处拉索完全损伤的概率由41.0%上升到47.5%，变化最为明显。在主塔加固后，整体刚度变大，塔的纵向变形减小，而从支座的易损性曲线可以看出主梁的纵向位移变化均值不大，因此为保证变形协调，拉索的索力最大值在整体上会变大。

主塔的关键截面易损性曲线如图16 所示。整体上桥塔除A—A 的主要截面的易损性曲线都有大幅度改善，其中B—B 截面和D—D 截面由于不在塔底，所受弯矩较小，在UHPC 的加固作用下即使PGV 达到200 cm·s-1，其轻微损伤的概率仅分别为2.4%和1.6%，而塔底C—C 截面在地震作用下虽然还是可能出现各种损伤情况，但当PGV 达到200 cm·s-1时，轻微损伤的概率下降了45.3%，中等损伤的概率下降了55.6%，严重损伤的概率下降了43.0%，完全损伤的概率下降了19.7%，说明采用UHPC 材料取得了良好的加固效果。

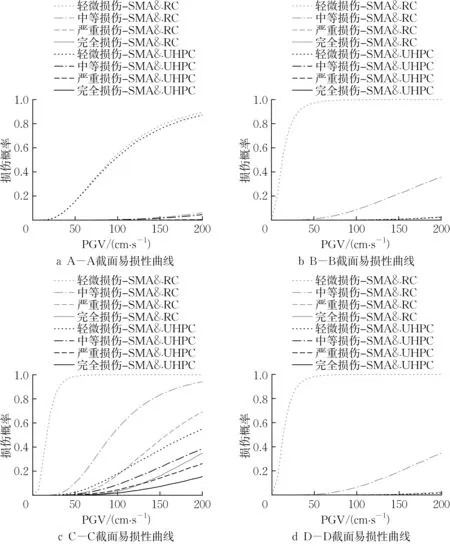
图16 SMA & RC- SMA & UHPC体系桥塔关键截面易损性曲线Fig.16 Vulnerability curves of key sections of SMA & RC- SMA & UHPC systems

4.6.2 结构易损性曲线

经计算后结构体系的易损性曲线如图17所示。在SMA 拉索减震装置限位作用和UHPC 材料的加固作用下，对于中等损伤，UHPC的加固作用的效果不是非常明显，但对于轻微、严重损伤和完全损伤的状态，UHPC 的加固作用使斜拉桥易损性均有了较大程度的改善：当PGV达到100 cm·s-1时，体系的严重损伤概率和完全损伤概率分别为41.4% 和17.2%，而当PGV达到200 cm·s-1时，体系的严重损伤概率和完全损伤概率相较于加固前分别降低了6.2%和9.7%。以上结果表明，UHPC 材料能明显降低SMA体系斜拉桥在强震作用下的损伤，能够控制和降低桥梁体系失效或倒塌的风险，为强震过后桥梁快速通车提供一定的安全保障，也为震后结构修复降低了修缮时间和经济成本。

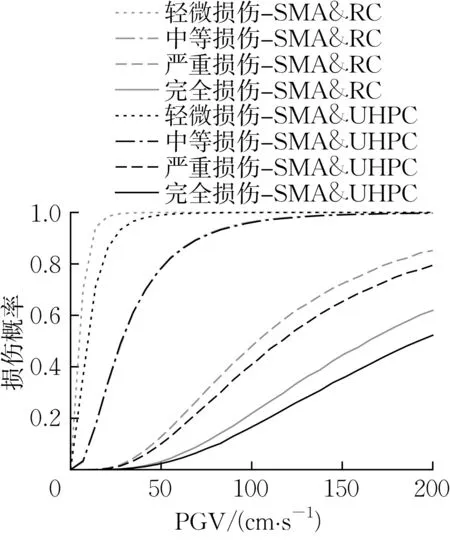
图17 斜拉桥SMA & RC- SMA & UHPC体系易损性曲线Fig.17 Vulnerability curves of SMA & RC - SMA &UHPC cable-stayed systems

5 结论

将SMA 拉索限位装置和UHPC 材料引入某大跨度斜拉桥，不仅对其动力特性进行了分析，还对该新型斜拉桥体系的易损性做了评估，得到如下结论：

（1） 不同位置的斜拉索在地震作用下的易损性有较大差别，需要具体分析，不能一概而论。

（2） 在地震作用下SMA 拉索不仅能够有效限制主梁产生过大的位移而降低支座的易损性，还可以有效防止斜拉桥的主梁与桥塔或引桥发生碰撞，缺点是会引起主塔截面的内力增大，进而引起主塔薄弱截面易损性的提高，基于此，本文将主塔薄弱区段的普通混凝土采用UHPC 材料进行替换，研究结果表明该方法可以显著降低桥塔的易损性。

（3） UHPC 材料的使用对支座易损性的影响不敏感，但斜拉索的易损性可能会相对增大，未来需提出降低斜拉索易损性的方法和具体措施。

作者贡献声明：

郑 越：提出论文框架，负责终稿修订，基金负责人。

王宇霄：有限元分析与计算。

郭军军：有限元程序的二次开发。

李方元：初稿修改。