高层建筑悬挂式电缆桥架模拟地震振动台试验

吴 宸， 笠井和彦， 蒋欢军， 松田和浩

（1.同济大学 土木工程防灾减灾全国重点实验室，上海 200092；2.同济大学 土木工程学院，上海 200092；3.东京工业大学 未来科技交叉研究所，东京 152-8550；4.名城大学 理工学部，名古屋 468-0073）

近年来，随着建筑抗震技术的发展，建筑遭受地震时主体结构的损伤得到了有效控制，但常常出现因非结构构件受损使建筑功能瘫痪［1］甚至人员伤亡的情况［2］。目前非结构构件的抗震研究相对滞后于结构构件［3］。民用建筑中非结构构件的投资占总建设投资的75%～85%［4］，而地震中的非结构构件往往会出现严重破坏。1971 年的美国圣费尔南多地震、1972 年马那瓜地震、1978 年日本宫城县地震都出现电梯大面积瘫痪的现象［5］。在2010年海地地震中，多层建筑的数据中心的电缆桥架损坏，难以快速修复，阻碍了震后基本通讯系统的恢复运行［6］。在2012 年东日本大地震中，东京高层建筑由于包括电缆桥架在内的大量非结构构件损坏导致建筑功能中断而产生所谓的“高层建筑难民”［7］。在2013年我国芦山地震中，经过抗震加固的建筑结构震害较轻，但依然观察到大量非结构构件的破坏［8］，其中包括电缆桥架。在2017年九寨沟地震中，高层酒店的玻璃幕墙面板出现大面积破损［9］。非结构构件的正常工作对于建筑功能的保持有着重要意义。

电缆桥架是一种用于线缆敷设的典型预制非结构构件，由电缆托盘、支吊架和连接件组成。电缆托盘通常为钢制或铝制，在转向区域的预制构件被称为弯通。核电站与其他工业建筑中的支吊架多采用通过型钢与下方地板或楼板固定的立式电缆桥架，而民用建筑通常采用悬挂式电缆桥架。电缆桥架具有大跨度、低冗余和复杂几何形状等特性，在地震激励下容易产生较大的响应与破坏。电缆桥架的抗震性能试验多采用足尺试件的模拟地震振动台试验。针对核电站与工业建筑中的桥架系统的代表性试验往往通过对不同的支架配置进行动力测试，识别电缆桥架每个方向的基频、阻尼、振型、疲劳寿命等［10］。试验结果表明，电缆桥架的响应表现出强烈的非线性，阻尼比随着输入地震的增大而增大［11］。由于福岛核电站的泄露事故，在2011年后国内也进行了大量与核电站有关的设备（包括电缆桥架）的振动台试验。胡服全等［12］通过振动台试验研究了核电站钢制电缆桥架抗震性能的影响因素。Huang等［13］通过足尺的振动台试验验证国内核电站使用的电缆桥架的阻尼比与载重之间的关系。另外，还有少量研究人员对普通民用建筑中的电缆桥架进行了试验研究。Wood 等［14］通过单调加载和循环加载方式研究了2类抗震支架的力与位移的关系，结果表明抗震支架与电缆托盘的连接构件对支架力与位移特性有显著影响。尚庆学等［15］对国内常用的抗震支架进行拟静力试验，通过易损性分析将各类抗震支架的极限承载力转化为对应的加速度指标。总体而言，目前国内外对核电站的电缆桥架的抗震性能研究较多，但针对高层建筑中常用的悬挂式电缆桥架的抗震性能研究较少，同时缺少对带有弯通段的立体式电缆桥架抗震性能的研究。

本文以高层建筑中常见的悬挂式电缆桥架为研究对象，进行了2组足尺模型的模拟地震振动台试验。第1组试验针对配置了3种不同类型抗震支架的电缆桥架研究不同抗震支架对抗震性能的影响；第2组试验针对1个带有水平弯通与竖向弯通的L形立体电缆桥架研究立体的电缆桥架和弯通段的抗震性能。

1 试验概况

1.1 振动台与加载钢平台

悬挂式电缆桥架试件安装在1个加载用的钢结构平台上，如图1所示。钢结构平台的X方向尺寸为12.84m，Y方向为11.64m，高度为5.40m，X方向的基本频率为8.9Hz，Y方向为8.4Hz。由于钢平面尺寸较大，使用同济大学多点振动台组中的2 个振动台，单个振动台台面X方向长4m、Y方向长6m，最大载荷为30t，可实现最大位移±500mm，最大速率±1 000mm·s-1，最大加速度±1.5g。2 个振动台在加载过程中保持同步运动。

图1 钢平台与振动台Fig.1 Steel platform and shaking table

1.2 试验试件

电缆桥架由电缆托盘与支架组成，试验中采用预制梯架式电缆托盘，主梁和次梁焊接相连，预制电缆托盘之间在现场采用连接件螺栓连接。电缆托盘通过支架悬挂在钢平台顶部下方，支架分为重力支架和抗震支架2种。重力支架只承担电缆桥架的重力，而以一定间隔设置的抗震支架需要同时承担电缆桥架重力和水平向的地震作用。此外，靠近弯通处也布置有抗震支架，电缆桥架示意图如图2所示。2组试验中使用相同的电缆托盘与重力支架，吊杆和支架长度为1.0m，电缆托盘宽度为1.0m，试件的重力支架的间距为2.0m。电缆托盘上放置钢筋，模拟电缆，线荷载为106.2kg·m-1。钢筋由尼龙扎带固定在电缆托盘上，钢筋底部铺设橡胶片，以使其摩擦与电缆的实际情况相近。

第1 组试验针对3 个安装有不同类型抗震支架的电缆桥架试件。3种抗震支架类型分别为型钢式、拉杆式和抗震强化式，3 个试件相互平行布置，分别称为A类、B类和SA类。其中A类和B类的抗震支架间距为8m，总长度为12m；而SA类的抗震支架间距为6m，总长度为10m。抗震支架的细节与尺寸如图3 所示，三者的纵向支架相同，以拉杆式支架为例，如图3d 所示，沿纵向两侧用拉杆固定。支架的拉杆直径均为14mm，型钢式和抗震强化式支架采用截面为75mm×75mm×6mm的角钢。3个试件抗震支架的信息如表1所示，通过拟静力试验得到2个方向的抗侧刚度。第2组试验针对带有水平弯通构件与竖向弯通构件的一个L 形立体电缆桥架。2 个桥架直线段根据走向命名为X向直线段和Y向直线段，X向直线段的抗震支架间距为8m，Y向直线段为6m，均采用型钢式抗震支架，2个直线段由水平弯通相连，并在Y向桥架末端设置一个竖向弯通。

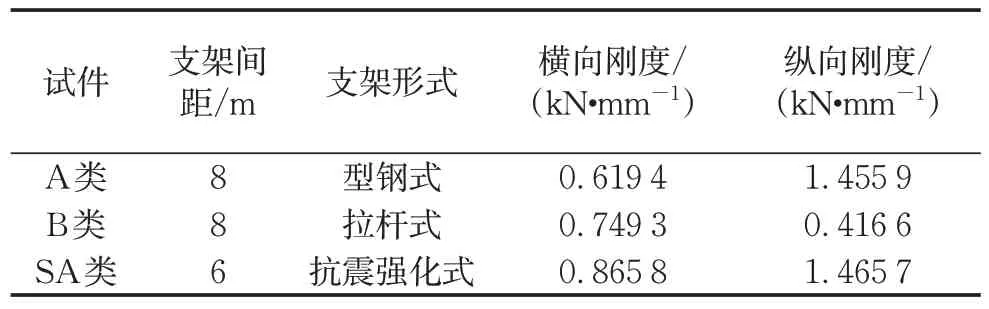
表1 抗震支架信息Tab.1 Information of seismic support

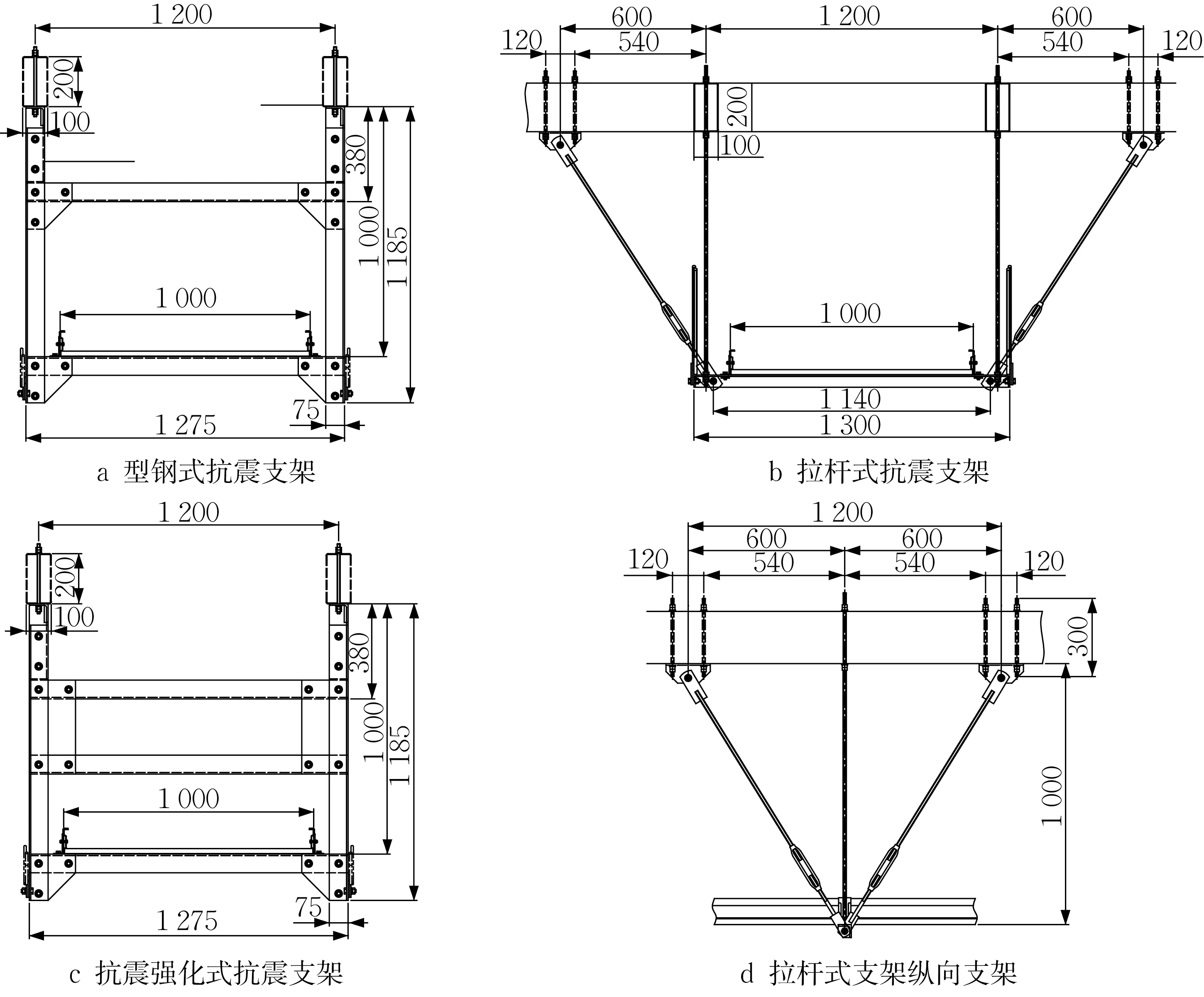
图3 电缆桥架抗震支架详图（单位：mm）Fig.3 Details of seismic support for cable tray (unit: mm)

1.3 传感器布置与加载方案

试件上设置有位移计和加速度计，具体布置如图4所示。位移计安装在钢平台上，通过拉线连接到电缆托盘侧面，测量值为测点与钢平台的相对位移。加速度计固定在电缆托盘底部，测量值为测点的绝对加速度。此外，钢平台和振动台上设置了部分加速度计用于记录振动台与钢平台的加速度，作为试件的输入信息。第2组试验在水平弯通的对角线方向共设置4个拉线式位移计，布置在水平弯通的上下方，用于测量其局部变形情况，如图4b所示。

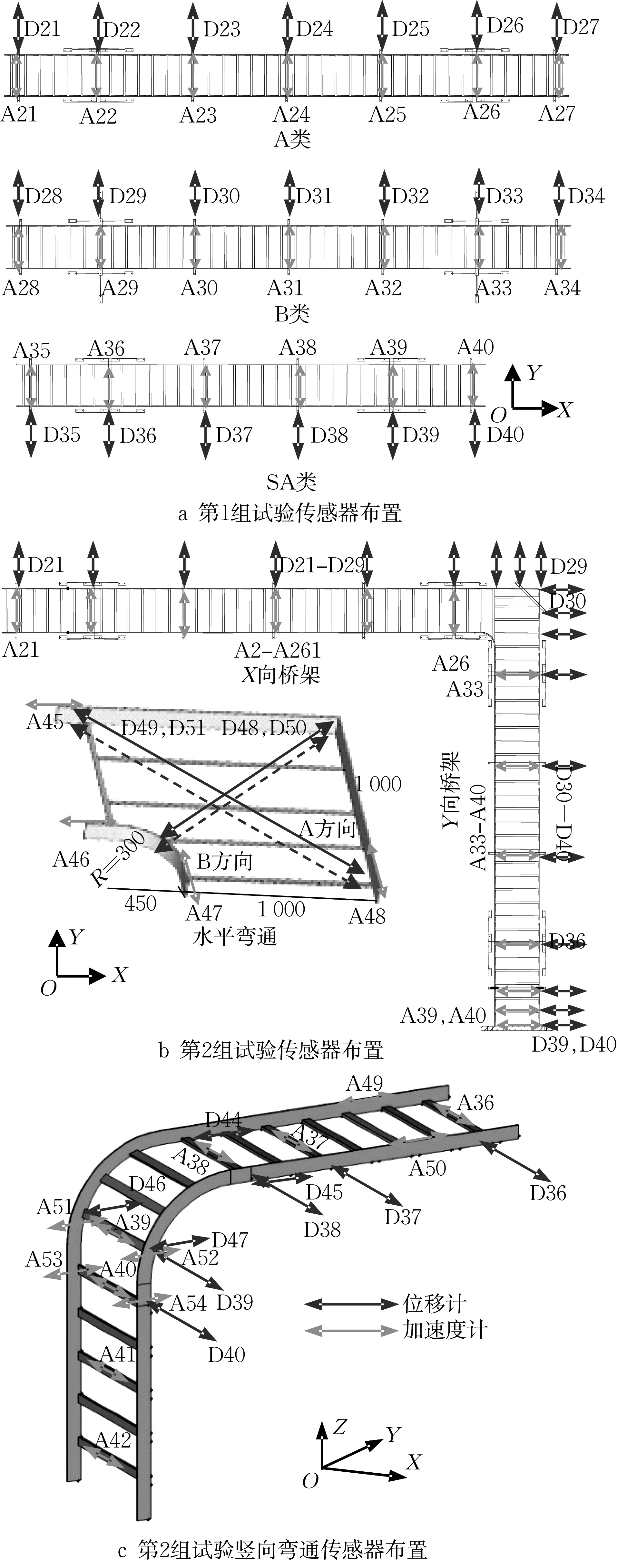
图4 传感器布置Fig.4 Arrangement of sensors

试验中输入了扫频波（sweep 波）和楼面波 2 种类型的地震波，此外在试验开始和每次加载工况后还采用峰值加速度为50 cm·s-2的白噪声，以测量电缆桥架的动力特性变化情况。第1组试验工况如表2所示，第2组试验工况如表3所示，白噪声为奇数工况，在表中省略。

表2 第1组试验输入工况Tab.2 Input motions for the first group of tests

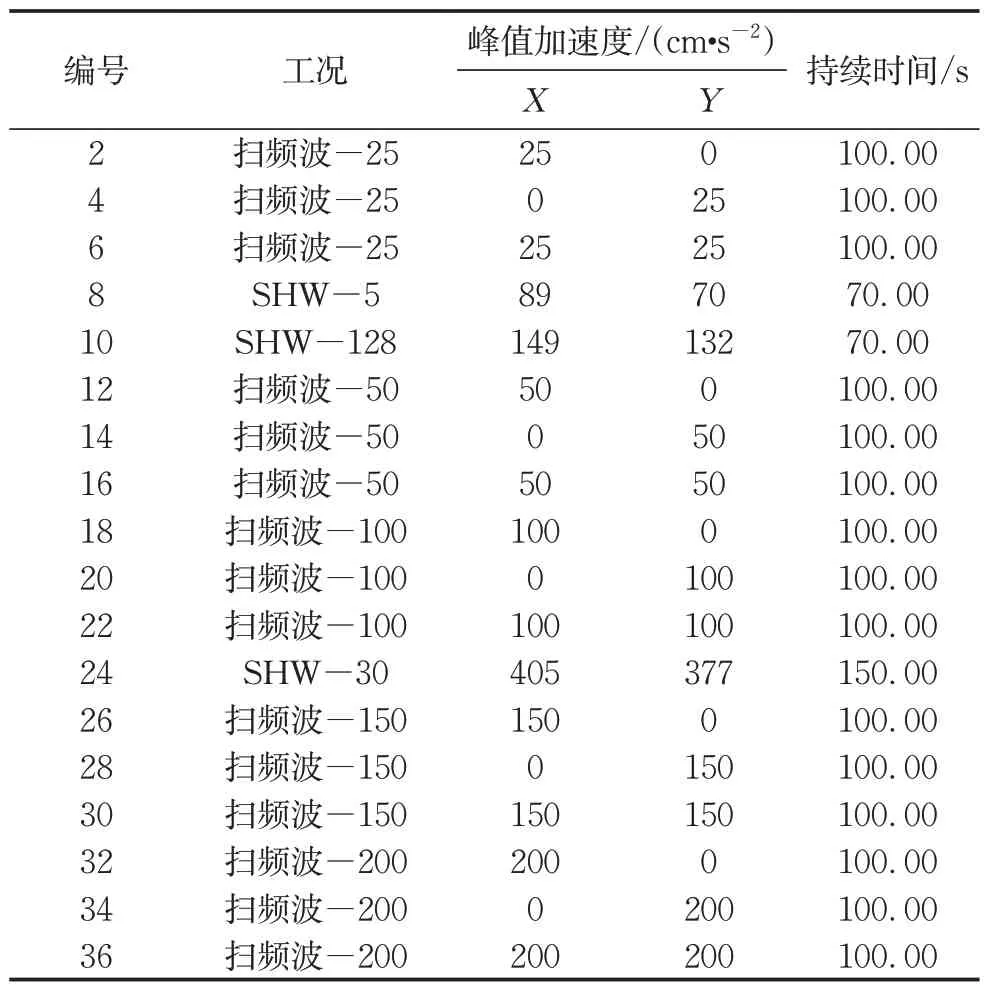
表3 第2组试验输入工况Tab.3 Input motions for the second group of tests

扫频波工况为峰值加速度不变、频率连续变化的正弦波，试验中频率由6Hz 逐渐变为0.8Hz。由于振动台控制的需求对扫频波的高频部分做了折减，频率的变化率为-1.74。根据美国非结构构件的振动台试验规范AC156［16］，扫频波变化率绝对值小于2 时，非结构构件有足够时间进入共振状态。试验中的扫频波的峰值加速度分别为50、100、150和200 cm·s-2。楼面波由2个高层建筑结构模型计算得到。将上海市标准《建筑抗震设计规程》［17］中的天然地震波SHW6（主方向的加速度峰值为0.1g）输入到128层的高层结构Benchmark模型［18］和30层的层间剪切高层结构模型中，计算得到2 个模型的楼面加速度响应，提取Benchmark 模型的第5 层及128层顶部的楼面加速度时程和层间剪切模型第30 层顶部的楼面加速度时程作为试件的输入波，3种楼面波分别命名为SHW-5（128层模型的第5层）、SHW-128（128 层模型顶部）和SHW30（30 层模型顶部）。128 层Benchmark 模型的前3 阶自振周期分别为8.94s、8.93s 和4.48s；30 层层间剪切模型的前3 阶自振周期分别为3.01s、1.18s和0.72s。楼面波输入可以体现高层建筑中电缆桥架地震输入特点。由于模型的动力特性差异，各模型不同楼面的加速度峰值和频谱特征差距较大，输入地震波情况见图5。

图5 输入地震波Fig.5 Input motions

2 试验结果与分析

2.1 试验损坏现象与基频变化

在第1组试验中，电缆托盘侧向摆动，托盘的主次梁节点焊缝逐渐开裂、失效，次梁在主梁上滑动，最终掉落失效，这是试验中观察到的最典型的损伤，如图6 所示。损伤首先集中出现在抗震支架附近，随后破坏逐渐向抗震支架两侧发展。A类试件的节点最终有约30%因为断裂而失效，左侧有2 根次梁连续出现掉落。B类最终有约20%的主次梁节点开裂，SA类最终有约15%的节点开裂。从3个试件的最终损伤情况来看，A 类的破坏比B 类严重，而SA类的破坏则显著轻于前两者，说明SA类的抗震能力最强，A类的抗震能力最弱。第1组试验各桥架最终的损伤分布如图7a所示。

图6 试件的损伤形式Fig.6 Damage types of specimens

在第2组试验中，由于桥架的弯通段被加强，弯通段的损伤不明显，桥架的损伤主要发生在直线段，主要集中在主次梁的节点上，最终约有40%的节点开裂、失效。在X向直线段上出现2 处连续的次梁掉落。第2组试验为双向输入，有更多的加载工况，导致开裂的主次梁节点比例比第1组大。观察预先设置的标记表明，试验过程中电缆桥架上的螺栓未出现松动。第2组试验中试件上最终的损伤区域分布如图7b 所示。2 组试验中均出现次梁的连续掉落，但电缆桥架未发生整体倒塌。

试验表明，在地震激励下，靠近抗震支架区域的电缆托盘容易破坏形成抗震薄弱部位。当抗震支架横向刚度增加时，电缆桥架的破坏会减轻。此外，当合理配置抗震支架时可显著减轻弯通段的损伤。

在白噪声工况下，以钢平台顶部时程为激励信号，通过最小二乘复指数法得到各测点的自振频率和阻尼比。在第2 组试验中，试验数据表明桥架并非整体振动而是各段桥架以不同频率振动，因此后续分析会根据抗震支架安装位置将桥架分为2个桥架直线段和2个弯通段，分别进行分析，以各段上测点的均值作为该试件段的动力参数，各工况下桥架的基本频率变化如图8 所示，阻尼比变化如图9 所示。随着试验进行，桥架的基本频率逐渐减小，阻尼比逐渐上升，表明电缆桥架试件逐渐发生破坏。

图9 桥架阻尼比变化Fig.9 Damping ratio change of cable tray

在第1 组试验中，3 个试件在第1 个白噪声工况下得到的基频分别为2.14、2.26 和2.97Hz，前期基频变化不明显，试件发生破坏后，频率突然开始下降且曲线斜率逐渐增加，体现了电缆桥架由于构件冗余小、破坏程度会迅速增大的特点。A 类试件频率的显著变化发生在SHW-30 工况（第12 工况），其基频下降了10.2%；B 类的试件频率在SHW-30 工况产生变化，基频下降4.7%，同时在扫频波-150 工况（第14工况）发生显著变化，基频下降13.9%；SA类试件频率的显著变化发生在扫频波-200 工况（第16工况），此工况之前抗震强化型的SA 类的试件损伤较小，此工况时主次梁节点开裂，刚度变化引起了频率的显著变化。3 个试件阻尼比显著变化均发生在SHW-30 工况（第12 工况），但是A 类的变化幅度最大，B 类次之。3 个试件的阻尼比分别从最初的9.29%、7.42% 和6.54% 变化为最后工况的20.23%、19.35%和17.07%，且与频率类似，在特定工况后发生显著变化。动力特性变化表明：型钢式的A 类与拉杆式的B类相比，不但更早产生破坏，最终的破坏也更严重；抗震强化式SA类损伤最晚发生且损伤程度最轻，此规律与前文损伤情况吻合。

在第2组试验中，X向和Y向桥架直线段的基频为2.25 和2.99Hz，试验后频率分别降低了48.34%和42.48%，而水平弯通和竖向弯通的基频为8.52和4.85Hz，频率分别降低10.20%和7.03%，弯通段的频率变化远小于直线段。X和Y向桥架直线段的初始阻尼比分别为6.19%和6.14%，最终的阻尼比为19.23%和19.85%，水平弯通和竖向弯通的初始阻尼比分别为2.71%和7.25%，最终的阻尼比为3.90%和8.37%。弯通段的阻尼变化较小，这表明弯通在试验中损伤较小。2 组试验中楼面波工况下频率和阻尼比变化不大，表明试验中典型的电缆桥架模型能承受七度设防地震作用，模型在扫频波工况出现破坏后，频率和阻尼比都会显著变化。

2.2 加速度响应

在扫频波工况中，输入地震波的频率逐渐变化而加速度幅值不变，以扫频波-100 工况为例，2 组试验的加速度时程如图10所示，图中右侧纵轴为扫频波的频率，桥架试件的加速度会出现明显放大的情况，此时可以得到扫频波的频率。这种加速度放大现象也反映出悬挂式电缆桥架对输入波频率的敏感性。美国非结构试验规范AC156［16］中提出使用扫频波进行试件的共振频率测试，能考虑存在电缆之间的相互摩擦以及电缆在托盘内相对运动的实际情况，测试中加速度响应峰值对应的输入频率被称为共振频率。而基频是在相同的较小的白噪声工况下得到的，此时电缆间以及与电缆托盘的摩擦属于静摩擦，因此基频结果只能反映电缆桥架构件自身的损伤情况。扫频工况下试件的共振频率与基频如表4 所示，共振频率会小于基频，且与输入的强度负相关。需要指出：在试件没有明显破坏、基频没有明显变化的工况下，共振频率就出现明显变化，说明共振频率的改变主要来自摩擦状态与相关的能量耗散的不同，而非试件的累积损伤破坏。在实际工程中，要避免共振频率与主体结构的基频靠近，避免电缆桥架与主结构共振而发生严重损坏。

表4 试件共振频率与基频Tab.4 Resonance and fundamental frequencies of specimen单位： Hz

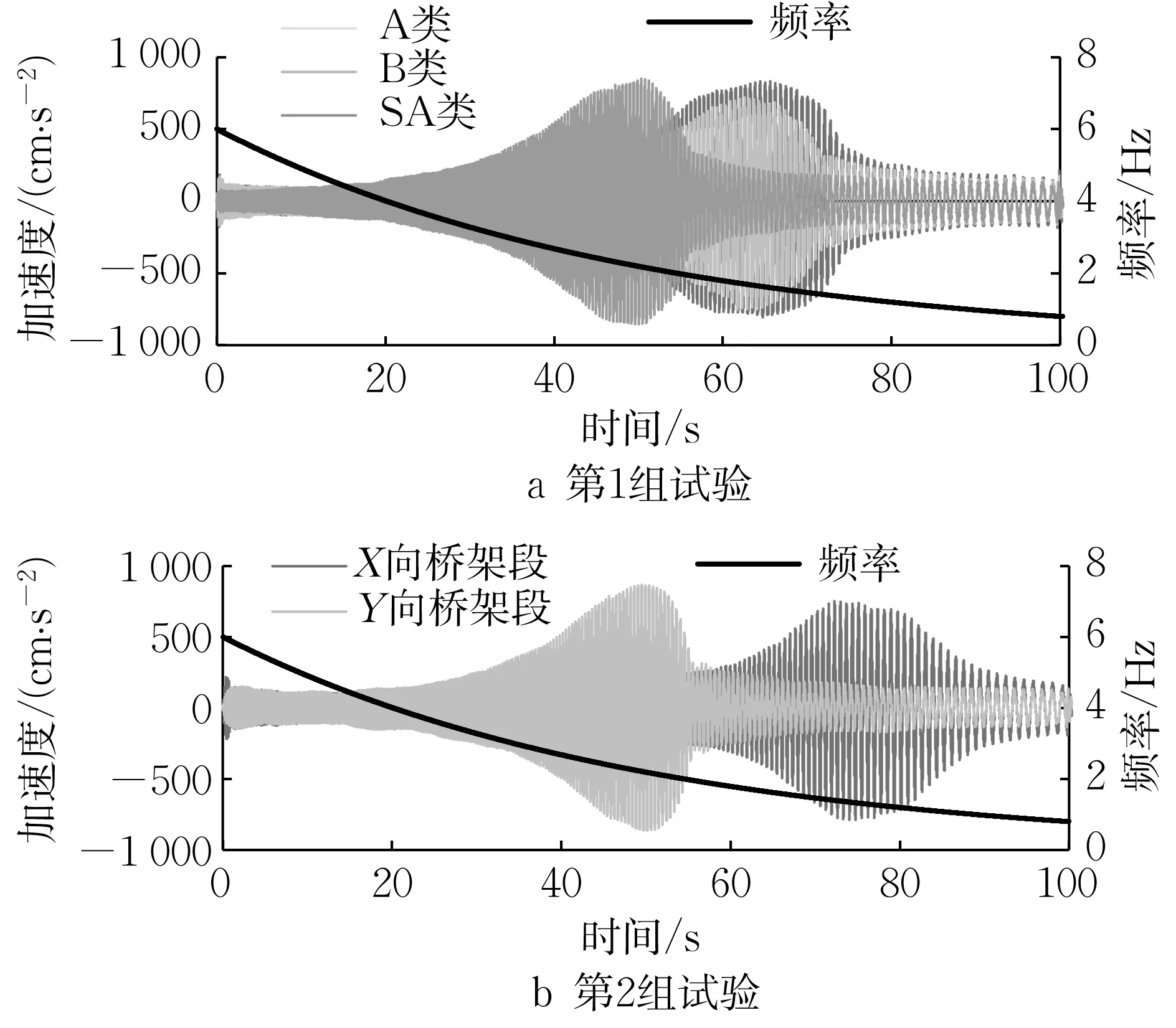
图10 扫频波工况加速度时程Fig.10 Acceleration time history of sweep waves

楼面波工况下试件的峰值加速度如表5 所示，试件的峰值加速度与钢平台顶部记录的楼面最大加速度（PFA）如图11。在楼面波工况下，SHW-128输入的峰值加速度几乎是SHW-5 的2 倍，但是两者最后的加速度峰值响应较为接近。这是因为SHW-128 的反应谱在电缆桥架的1 阶周期（0.3～0.5s）的谱加速度较小，如图5所示。不只是加速度峰值，主体结构的楼面波频谱成分也会对电缆桥架的加速度响应产生影响。SHW-30的输入和峰值加速度响应都明显更大。在各加载等级的扫频波下，不同抗震支架的桥架的峰值加速度响应差别较小，加速度峰值随输入增大而逐渐增大，基本随PFA 线性变化。同时，弯通段的加速度响应峰值显著小于直线段，水平弯通段的加速度响应显著小于竖向弯通段。

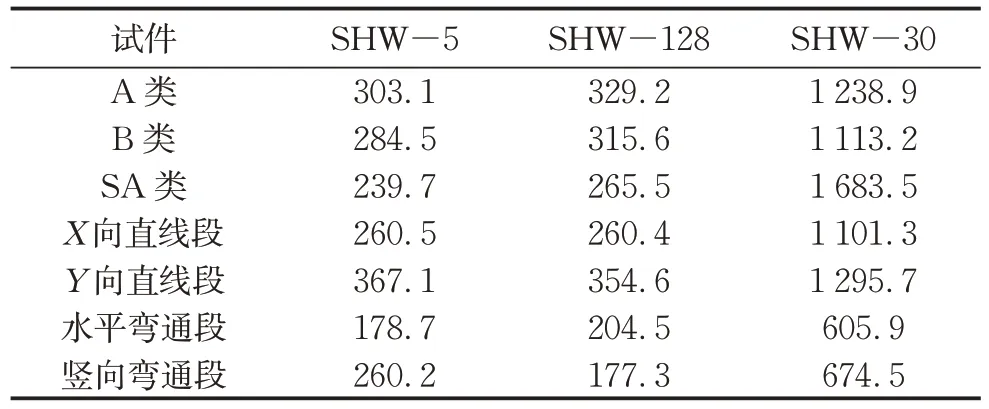
表5 楼面波工况下的峰值加速度Tab.5 Peak acceleration under floor waves单位：cm·s-2

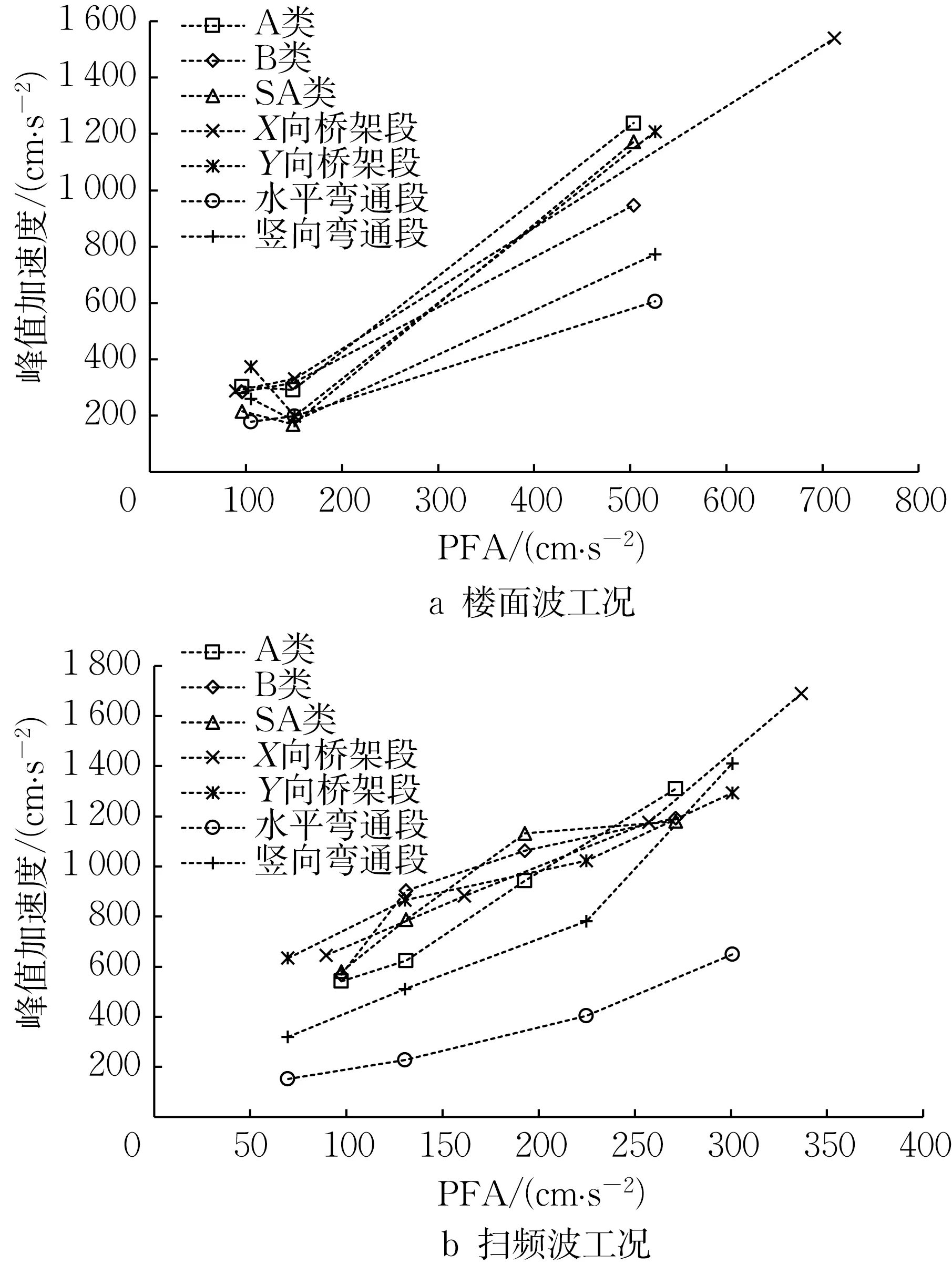
图11 试件峰值加速度与楼面最大加速度Fig.11 Peak acceleration of specimen and floor acceleration

2.3 构件加速度放大系数

构件加速度放大系数（AAF）又称为共振系数或状态系数，代表非结构构件的加速度响应相对于楼面加速度的动力放大，放大同时受到主体结构与非结构构件动力特征的影响。试验中的AAF 表示为试件测点的最大加速度与楼面峰值加速度的比值。《建筑抗震设计规范》［19］中电缆桥架AAF 的推荐值为2.0，美国规范ASCE 7 和欧洲规范EC8 规定AAF 的推荐值分别为2.5 和2.0［13］。表6 给出了楼面波工况下各试件的AAF，由于频谱特征对AAF有显著影响，只有楼面波激励下的AAF才具有与规范推荐值相比的可比性。假定AAF符合正态分布，根据试验AAF 的均值和方差能得到根据中国规范推荐值取2.0 所对应的保证率。从表中数据可知，在设防地震动下悬挂式电缆桥架的加速度放大系数的均值小于规范的推荐值，弯通段的保证率较高，但其他直线段桥架的保证率较低，约为60%～70%。在同一个楼面波输入下，3种抗震支架的电缆桥架的AAF差异较小，而不同楼面波下AAF差异较大。

表6 楼面波工况的加速度放大系数Tab.6 AAF of floor waves

2.4 位移响应

在第1 组试验中，电缆桥架试件位移响应如图12所示，抗震支架能限制电缆托盘的侧向位移，电缆托盘侧向变形整体为抛物线形，最大位移响应出现在跨中。各段桥架的测点侧向位移响应峰值如图13所示。对于扫频波-200 工况，预期位移会超出位移计量程，试验前移除了位移计，因此未测量此工况下的位移。

图12 第1组试验位移响应Fig.12 Displacement response of the first group test

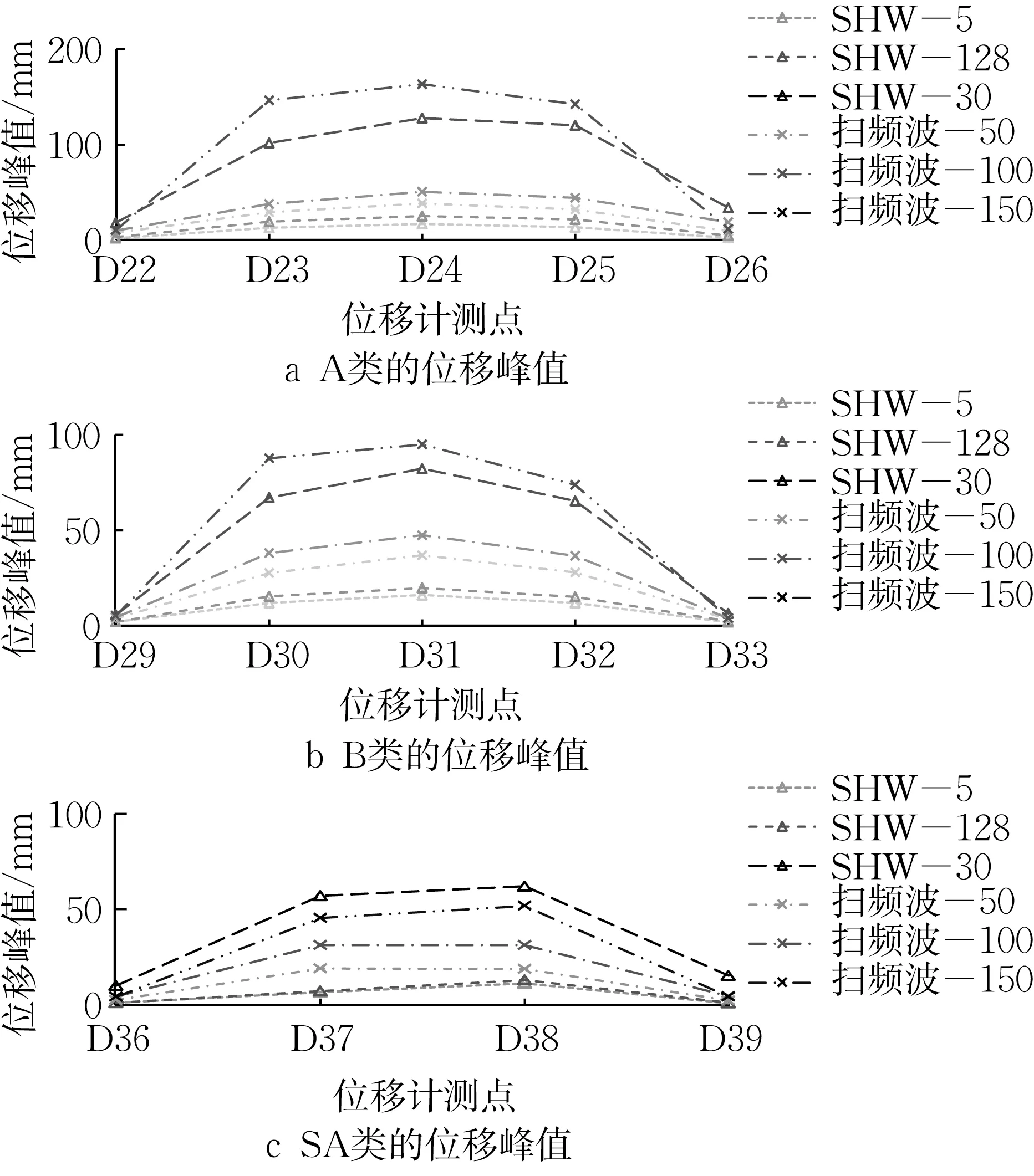
图13 第1组试验侧向位移峰值Fig.13 Peak lateral displacement of the first group test

结果表明，A类试件的位移响应大于B 类，且两者抗震支架间距相同，说明拉杆式抗震支架的位移控制效果好于型钢式抗震支架。SA 类试件的侧向位移响应最小，说明增大抗震支架抗侧刚度并减小布置间距可以减小电缆桥架的侧向位移响应。各试件侧向位移响应峰值与PFA 的关系如图14 所示。随着PFA的增大，桥架侧向位移增大。在相同PFA下，扫频波工况下侧向位移响应会显著大于楼面波工况下的响应。

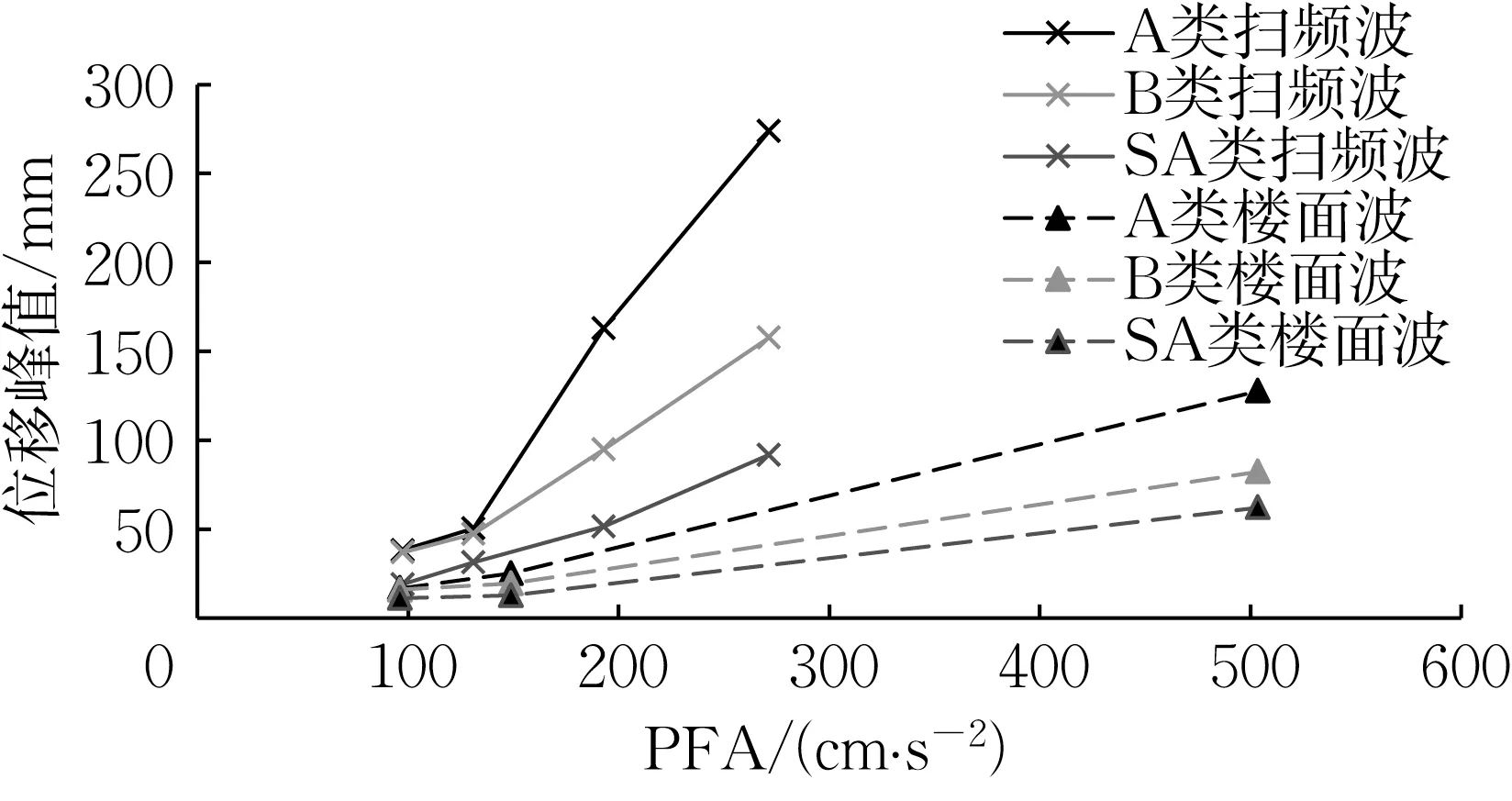
图14 桥架侧向位移峰值随PFA的变化情况Fig.14 Overall peak displacement and PFA

在第2组试验中，桥架直线段的位移响应与第1组试验中相似，而水平和竖向弯通段的位移响应远小于直线段。此外从视频记录可知，两方向的直线段在地震输入下以不同的频率局部振动，而非以一个频率整体运动，水平弯通无法协调两者的运动。在第2 组试验中，直线段和弯通段的位移响应如图15所示。各直线段和弯通段的侧向位移响应峰值如图16 所示。由于自身较大的刚度和相连的抗震支架，水平弯通的最大位移仅为9.5mm，竖向弯通的最大位移仅为21.3mm，远小于桥架直线段的位移响应。2个弯通段的位移响应在抗震支架附近较小，说明抗震支架能有效减小弯通段的位移响应。

图15 第2组试验位移响应Fig.15 Displacement response of the second group test

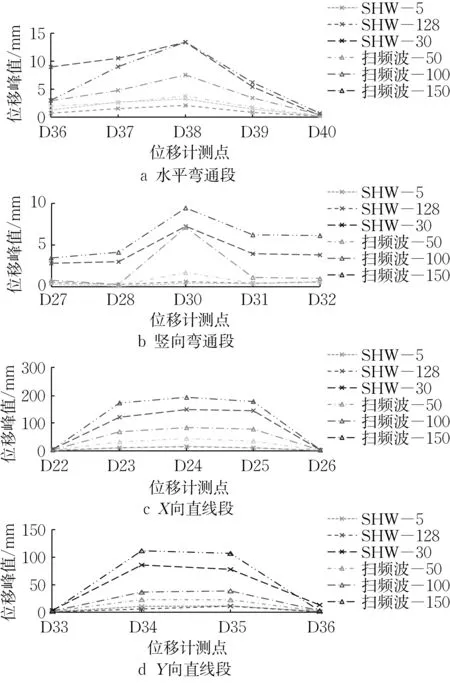
图16 第2组试验侧向位移峰值Fig.16 Peak lateral displacement of the second group test

引入支架间位移角θi作为桥架相对变形的指标［20］，对于直线段桥架和竖向弯通，支架间位移角为

式中：ui为第i个支架处的侧向位移；lsh为支架间距。对于水平弯通，则表示为

式中：δA和δB分别是在本试验中水平弯通方向A 和方向B 的2 个位移计均值的变化量。从表7 的支架间位移角的结果可知，不同的抗震支架配置会显著改变桥架相对变形情况，A类试件的相对变形大于B类，说明拉杆式抗震支架的相对变形控制效果好于型钢式抗震支架，而在SA 类试件的抗震支架配置下，桥架相对变形最小。在相同输入下，弯通段的相对变形显著小于直线段，损伤较轻。在SHW-30 和扫频波输入下X向直线段的位移角均显著大于Y向直线段；在楼面波SHW-5 和SHW-128 输入下，2 个方向的直线段位移角较为接近，主要原因是输入的地震波具有不同的频谱特征。此外，2个方向的直线段桥架的抗震支架间距不同，说明输入地震波的频谱特征和抗震支架间距会显著影响电缆桥架变形。

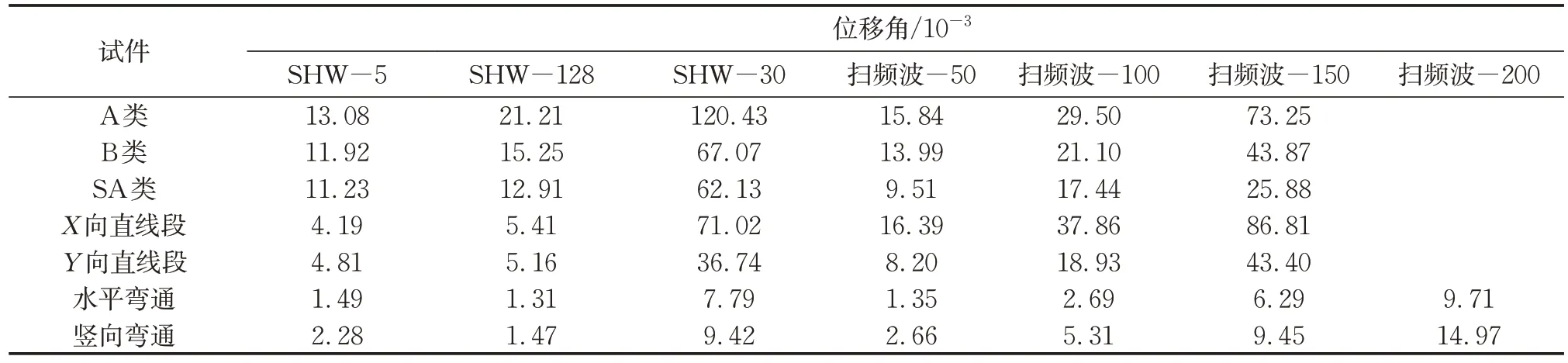
表7 支架间位移角Tab.7 Displacement angle between supports

3 结论

通过模拟地震振动台试验研究高层建筑中的电缆桥架在地震作用下的动力响应与破坏机理，可知：

（1）悬挂式电缆桥架的地震损伤主要表现为主次梁连接节点的开裂和失效，进而导致次梁掉落。抗震支架附近的节点最早开裂，之后裂缝逐步扩展至其他部位的主次梁节点。楼面波工况下试件的频率和阻尼比变化不大，电缆桥架试件在七度设防地震动输入下破坏不显著；在较大的扫频波输入后，电缆桥架破坏显著，频率降低而阻尼比上升显著。提高抗震支架附近桥架主次梁节点的强度有助于改善桥架的抗震性能。

（2）拉杆式抗震支架相较于型钢式抗震支架具有更好的抗震效果，且安装更为简捷。抗震强化式抗震支架同时减小抗震支架间距并加强支架刚度，抗震性能最佳。增加抗震支架横向刚度可以减小电缆桥架的损伤。不同类型的抗震支架对桥架试件的位移响应和损伤情况影响较为明显，而对加速度响应的影响相对较小。

（3）扫频波下得到电缆桥架的共振频率，共振频率小于基频，且随着输入地震动加速度的增大而减小。在实际工程中需要避免电缆桥架的共振频率与主体结构的基频靠近。

（4）试验得到的高层建筑中电缆桥架的加速度放大系数均值小于中国规范取值2，但是对应的保证率不高，实际设计中可以考虑适当提高取值。电缆桥架的加速度放大系数受输入地震动的频谱特征和加速度幅值大小影响，随着输入地震波加速度幅值的增大而逐渐减小。

（5）对于带弯通的电缆桥架，桥架的弯通段与直线段各自发生局部振动，弯通段的位移和加速度响应显著低于直线段的响应，且弯通段的损伤不明显。

作者贡献声明：

吴 宸：试验设计，数据分析，撰写初稿。

笠井和彦：项目构思，课题指导。

蒋欢军：项目构思，课题指导，论文审阅与修改。

松田和浩：试验设计，课题指导。