化归思想在初中数学“图形与几何”解题中的应用

娄凌翔

【摘  要】  化归思想是对几何形状求解的一种重要方法，适用于各种不同的几何问题.本文对化归思想在初中数学“图形与几何”中的具体体现进行梳理，以具体例子为依据，介绍化归思想在初中几何中的应用方法，并强调其在初中数学中的重要性，希望可以帮助初中学生更好地理解和应用化归思想.

【关键词】  化归思想；初中数学；解题教学

1  化归思想在“图形与几何”解题中的应用

1.1  平行线的性质

平行线的性质处在七年级下册的第五章，平行线的知识可以说是后续几何学习的基础知识，三角形内角和定理、平行四边形性质、相似三角形等都运用了平行线的性质.在难以解决这些问题时，可尝试将其转化为平行线问题.在平行线性质的应用中亦蕴含化归的思想.

例1  如图1，，若，，则

图1

解析  作，

因为，

根据平等的传递性，所以，

所以，，

又因为，，

所以.

图2

分析  从所给图形上看，没有一条直线截AB与CD，所以无法直接运用平行线的相关性质.故需使用构造法构造出“两条直线被第三条直线所截”的基本图形后，才能运用平行线的性质.本题转化是通过作，根据平行线的定理推论可知，由此构造出了直线AB，EF被BE所截，EF，CD被EC所截，这样就将问题转化，可使用平行线的性质解决问题.此外，本题还有另一种思路：直接构造与AB，CD都相交的截线.但这种思路需用到三角形的内角和，相较于本题的解题方法更复杂.

从分析过程中我们可以看出，问题的解决有多种转化的思路，但要提高解题的效率就需要找到最简的转化方式.这离不开对数学知识技能和化归思想方法的掌握和灵活运用.

2.2  全等三角形

平行线的性质在八年级上册的第二章，在研究全等三角形时，通过借助辅助线将一个三角形划分为若干个部分，然后用这些部分来构造另一个全等的三角形，以全等三角形作为解题的突破点.

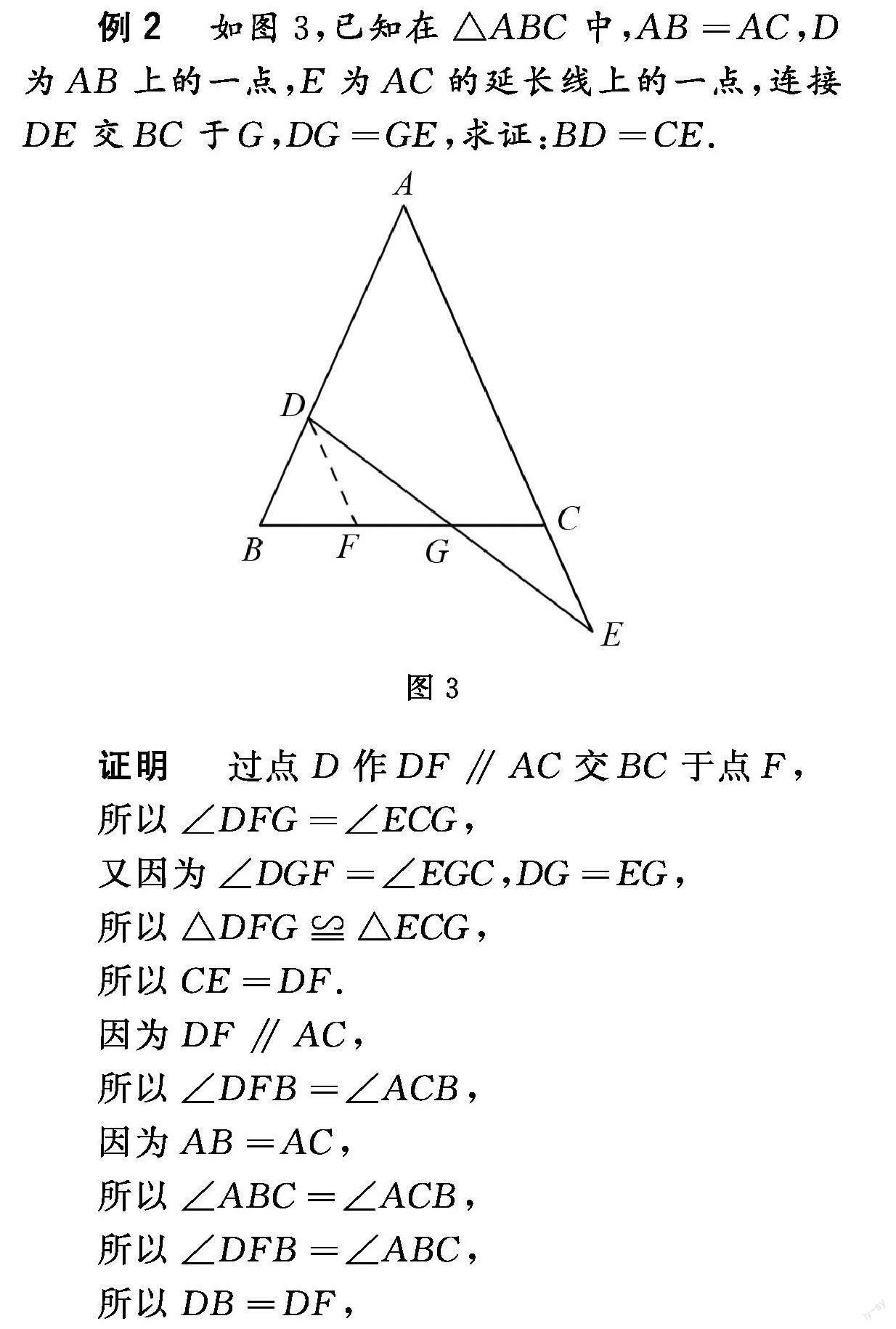
例2  如图3，已知在中，，D为AB上的一点，E为AC的延长线上的一点，连接DE交BC于G，，求证：.

图3

证明  过点D作交BC于点F，

所以，

又因为，，

所以，

所以.

因为，

所以，

因为，

所以，

所以，

所以，

所以，得证.

分析  因为本题要证明，但根据图形可以发现BD和CE这二者没有太多的联系，仔细观察发现可以通过构建全等三角形即可解得.

2.3  多边形的内角和

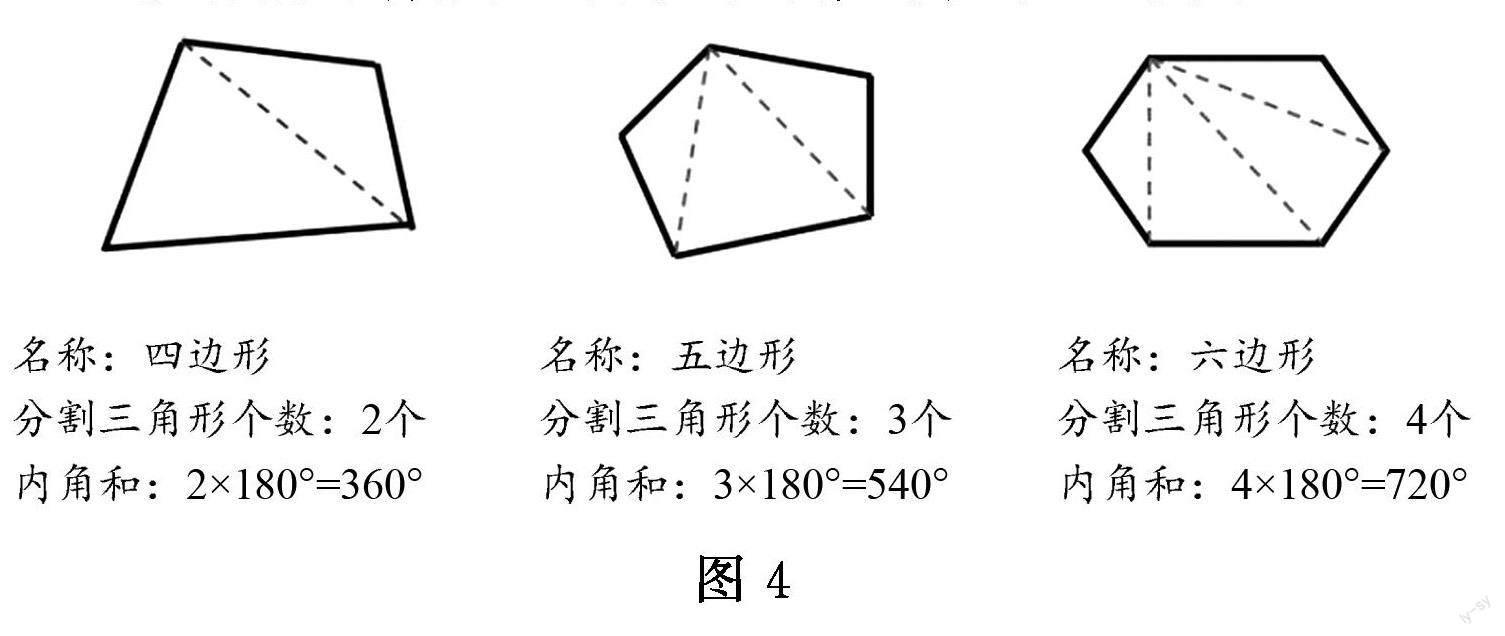
多边形内角和编排在八年级上册第十一章.多边形内角和及有关知识的学习基于三角形内角和知识，借助作辅助线将多边形划分割为多个三角形，将求多边形内角和的问题转化为求多个三角形内角总和，体现了化归思想.

多边形内角和的公式的推导如图4所示.

图4

通过观察规律可发现：从一个顶点引对角线，能把边形分成个三角形，个三角形的内角总和即为边形的内角和，即边形的内角和等于.

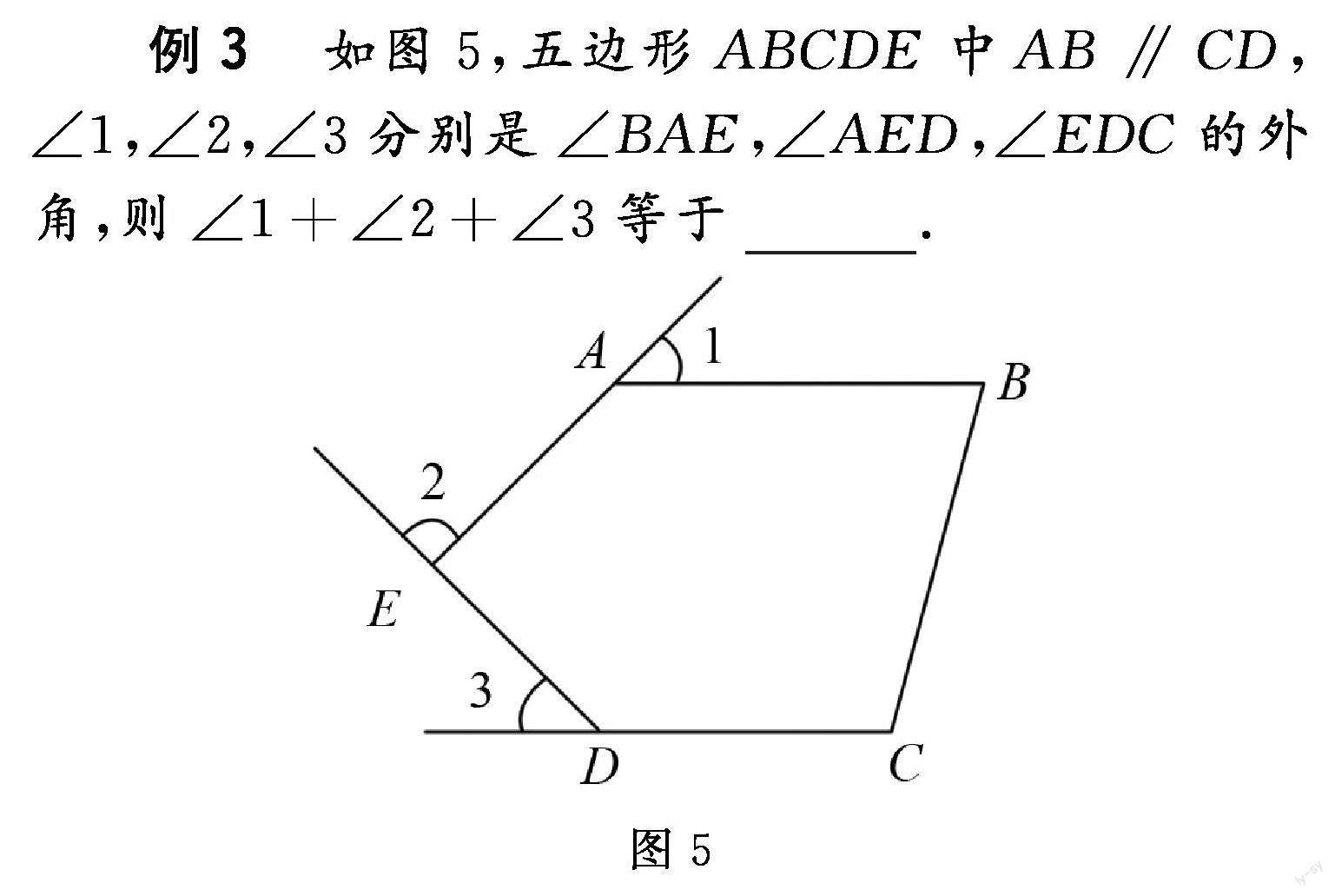
例3  如图5，五边形ABCDE中，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则等于    .

图5

解析  这道题是一个较为综合性的题目，包含了多边形内角和与平行线相关的知识点，我们需要结合图形仔细观察题干中所給条件，提炼出关键信息.

由五边形ABCDE可知内角和为，已知AB∥CD，由平行线同旁内角的性质可知：.

由此可将求多边形外角和的问题转化为求多边形内角和的问题.可得到.

2.4  矩形性质与判定的应用

矩形性质与判定编排在八年级下册第十八章.在研究平行四边形问题时，发现平行四边形的性质同样可以通过三角形的全等形来证明.所以，我们常将其化归为全等三角形问题来研究.矩形是一个角是直角的平行四边形，它具有平行四边形的所有性质.因此，在研究矩形时，常常将其化归为全等三角形问题进行研究.

例4  如图6，在四边形ABCD中，，垂足为点E，求证：.

图6                     图7

证明  如图7，过点B作于点F，

因为，

所以，

因为，

所以，

所以.

在和中，

所以，

又因为，，，

所以四边形AEFB是矩形，

所以，

所以.

分析  在上述证明过程中，主要采用构造法对图形进行几何变换.通过作辅助线构造全等三角形，化隐为显，将证明线段相等的问题转化成证明三角形全等及矩形对边相等.然后通过全等三角形的性质得到边与边之间的相等关系.

3  结语

数学问题的步步转化无不遵循着化归思想，利用化归思想将复杂问题简单化、未知问题熟悉化、抽象问题具体化是数学解题的捷径之一.因此，在初中阶段及时培养学生掌握基本知识技能，渗透数学思想，使学生将化归思想内化为独立获得知识和解决问题的能力就尤为关键.