基于COOT-SVM的短期光伏发电功率预测
陈晓华,王志平,吴杰康,许海文,陈盛语,张勋祥,龙泳丞,谢明钊
(1. 东莞理工学院电子工程与智能化学院,广东 东莞 523808;2. 广东工业大学自动化学院,广东 广州 510006)
0 引 言
2020年9月,中国在联合国大会上提出了“双碳”的目标:在2030年之前实现“碳达峰”以及在2060年之前实现“碳中和”的目标[1]。在“双碳”目标的引领下,具有获取方便、取之不尽、用之不竭和低污染等优点的光伏发电将逐步取代传统的化石能源发电。随着光伏发电技术的不断成熟,使用太阳能发电逐渐成为人类能源需求的首选绿色清洁新能源。然而,光伏发电具有随机性、波动性和间歇性等缺点,因此,提高光伏功率预测的准确率有助于电网的安全稳定运行、提高光伏发电并网能力、有效减少弃光和提高电网运行的经济性[1-6]。
现有的大部分文献对光伏功率预测的方法主要有直接预测和间接预测两种[7]。直接预测的方法只需光伏功率的历史数据和气象信息就能够对光伏功率进行预测,此方法主要包括前馈神经网络算法(back propagation,BP)[8-14]、支持向量机(support vector machine,SVM)[5,15-18]和组合预测法[19]等。间接预测的方法是基于物理法预测太阳辐射等气象因素,根据光电转换效率得到光伏发电的输出功率[20]。但神经网络算法容易陷入局部最优解并且算法耗时较长,使得光伏发电功率预测很难快速得到最优解;支持向量回归预测模型能够很好地解决预测值偏差过大和局部最优等问题,但核函数的参数和惩罚因子数值的选择对预测结果影响较大;组合预测法可以获得较高精度的光伏功率预测,但计算模型复杂并且消耗时间较长;使用间接预测法对太阳辐射等预测值的准确度要求较高。
针对以往研究的不足,下面建立了基于白冠鸡优化算法(coot optimization algorithm,COOT)优化SVM的预测模型来提高光伏发电功率短期预测的精度。选取某光伏电站在2017年春季中的4月前21天和夏季中的7月前21天的数据进行仿真;利用皮尔逊相关系数公式可以计算得到对光伏发电影响较大的因素为太阳总辐射强度、太阳散射辐射强度、太阳直射辐射强度、组件温度和环境温度5个气象因素,将它们作为输入数据,光伏发电功率作为输出数据,并对输入和输出的数据进行归一化处理;最后,利用COOT-SVM预测模型实现光伏发电功率的短期预测,对比COOT-SVM预测模型与BP和SVM预测模型,可知COOT-SVM预测模型具有较高的预测精度。
1 影响光伏发电预测结果的因素
光伏发电的日变化周期比较强,其输出功率会受各种气象因素的影响。太阳总辐射强度、太阳散射辐射强度、太阳直射辐射强度、组件温度、环境温度、相对湿度和气压等参数对光伏发电均有不同程度的影响。准确详细的输入数据是提高预测精度的关键,但输入数据过多会使预测过程更加复杂。因此以训练样本数据来计算光伏输出功率与各个气象因素之间的皮尔逊相关系数,计算表达式[2]为
(1)
式中:Xpv为光伏输出功率;Ymet为气象因子;Npv为光伏输出功率数据样本的数量;Nmet为气象因子数据样本的数量。
一般而言,两个变量的相关程度由以下范围判断:当0≤|r|<0.2,为极弱相关或不相关;当0.2≤|r|<0.4,为弱相关;当0.4≤|r|<0.6,为中等程度相关;当0.6≤|r|<0.8,为强相关;当0.8≤|r|≤1.0,为极强相关。
选取某光伏电站在2017年春季中的4月前21天和夏季中的7月前21天的相关气象因素历史数据和光伏发电系统输出功率历史数据作为研究对象,计算其光伏输出功率与每一个气象因素的相关系数,见表1。由表1可知:
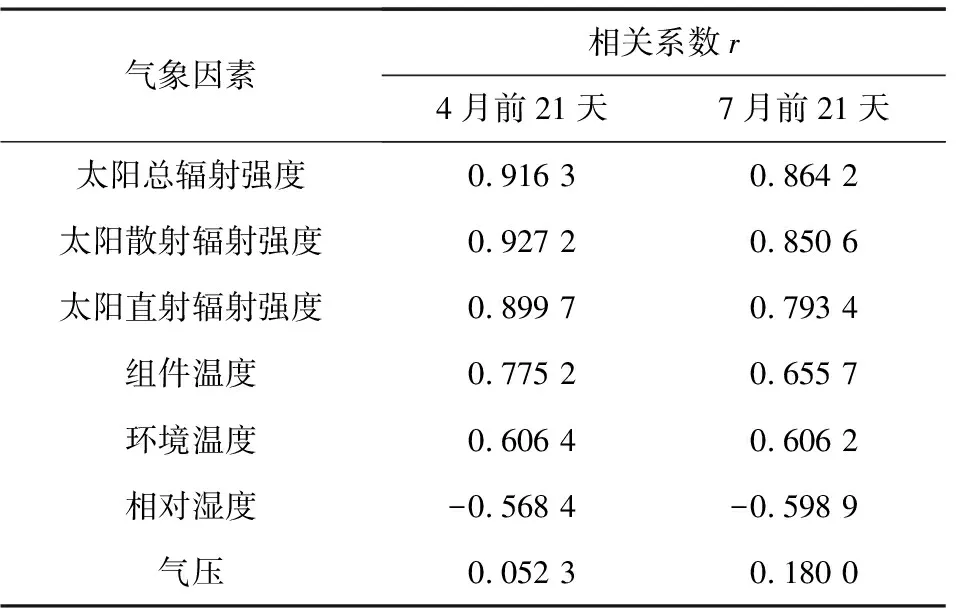
表1 光伏输出功率与各个气象因素的相关系数
1)该地区4月训练样本时间段内太阳总辐射强度、太阳散射辐射强度和太阳直射辐射强度3个气象因素与光伏输出功率极强相关;组件温度和环境温度两个气象因素与光伏输出功率强相关;相对湿度与光伏输出功率中等相关(负相关);气压与光伏输出功率极弱相关。
2)该地区7月训练样本时间段内太阳总辐射强度和太阳散射辐射强度两个气象因素与光伏输出功率极强相关;太阳直射辐射强度、组件温度和环境温度3个气象因素与光伏输出功率强相关;相对湿度与光伏输出功率中等相关(负相关);气压与光伏输出功率极弱相关。
因此,对于该地区春季4月和夏季7月的短期光伏功率预测,均选择太阳总辐射强度、太阳散射辐射强度、太阳直射辐射强度、组件温度与环境温度5个气象因素作为预测模型的输入数据,光伏发电功率作为输出数据。
2 白冠鸡优化算法的原理
在2021年由Naruei I等人提出的COOT优化算法[21]主要模拟白冠鸡在自然界中获取食物的行为,从而实现算法寻优的目的。该算法假设白冠鸡种群中有N个个体,从中选取10%的个体作为白冠鸡的领导者,剩余的白冠鸡为跟随者。
对白冠鸡种群领导者的位置进行初始化的计算表达式为
xLD,s,j=xL,j+ηs,j·(xU,j-xL,j)
(2)
式中:xLD,s,j为第s只白冠鸡领导者在第j维上的位置,s=1,2,…,NLD,NLD为白冠鸡领导者的数量,并且NLD=0.1N;ηs,j为在[0,1]区间上第s行第j列的一个随机数;j=1,2,…,d,d为待优化问题的维数;xU,j、xL,j分别为搜索空间中第j维变量的上限和下限。
对白冠鸡跟随者种群个体进行初始化的计算表达式为
xi,j=xL,j+ηi,j·(xU,j-xL,j)
(3)
式中:xi,j为第i只白冠鸡跟随者在第j维上的位置,i=1,2,…,Ncoot,Ncoot为白冠鸡跟随者种群大小,并且Ncoot=N-NLD;ηi,j为在[0,1]区间上第i行第j列的一个随机数。
该算法中,白冠鸡的行为主要包含以下4种:
1)个体随机移动
令白冠鸡跟随者种群朝搜索空间中的一个随机位置移动,随机位置的计算表达式为
(4)
式中,η1,j为在[0,1]区间上第1行第j列的一个随机数。
随机运动有利于算法跳出局部最优解,使用这种方法更新白冠鸡跟随者位置的计算表达式为
(5)
式中:R2为在[0,1]区间上的随机数;Tcur和Tmax分别为当前迭代次数和最大迭代次数。
2)链式运动
两只白冠鸡跟随者的平均位置可以实现链式运动,计算表达式为
(6)
式中,xi-1,j为第i-1只白冠鸡跟随者在第j维上的位置。
3)根据种群的领导者调整位置
通常情况下,白冠鸡跟随者种群必须根据白冠鸡领导者的位置调整自己的位置并且朝着它们的方向移动,这里利用k来控制白冠鸡领导者的位置引导作用。
k=1+mod(i,NLD)
(7)
式中:i为第i只白冠鸡跟随者的序号;mod(i,NLD)的含义为i对NLD取模;k为白冠鸡领导者的序号。
因此白冠鸡跟随者的位置更新为
(8)
式中:R1为在[0,1]区间上的随机数;R为在[-1,1]区间上的一个随机数;xLD,k,j为第k只白冠鸡领导者在第j维上的位置。
4)白冠鸡领导者带领白冠鸡跟随者走向最佳区域
白冠鸡种群的领导者不断更新它们朝着最佳区域目标方向的位置,从而带领白冠鸡跟随者种群走向最佳区域,白冠鸡领导者的位置更新计算表达式为
(9)
式中:gbest为种群内个体的最优位置;R3和R4为在[0,1]区间上的随机数。
3 白冠鸡优化算法优化SVM参数的预测模型
3.1 支持向量机(SVM)
由于篇幅有限,不再对SVM的预测理论进行推导,具体步骤可以参考文献[17]。因为SVM的预测结果在很大程度上受惩罚因子和核函数中参数的影响[17],所以采用白冠鸡优化算法对这两个参数进行寻优,从而提高短期光伏发电功率预测的精度。
3.2 白冠鸡优化算法优化SVM参数
利用COOT算法对SVM的参数进行优化的步骤如下:
1)利用式(2)和式(3)分别初始化白冠鸡领导者和跟随者数量。设置白冠鸡种群的个体数N=50,其中白冠鸡领导者的数量NLD=5,白冠鸡跟随者的数量Ncoot=45,最大迭代次数Tmax=30,待优化问题的维数d=2,搜索空间的上限xU,1=xU,2=100,下限xL,1=xL,2=0.01。
2)计算白冠鸡领导者和白冠鸡跟随者的适应度函数,找出白冠鸡种群内个体的最优位置gbest,记下此时的适应度函数值为fcoot(gbest)。
3)计算A和B的值。随机生成一个在[0,1]区间上的随机数r1,若r1<0.5,则R、R1和R3均为1行d列的随机向量;否则,R、R1和R3均为随机数。
4)计算白冠鸡领导者的序号k。
5)随机生成一个在[0,1]区间上的随机数r2,若r2>0.5,则利用式(8)计算白冠鸡跟随者个体的位置;否则,跳到步骤6。
6)若r2<0.5&&i≠1,则利用式(6)计算白冠鸡跟随者个体的位置;否则,利用式(4)和式(5)计算白冠鸡跟随者个体的位置。
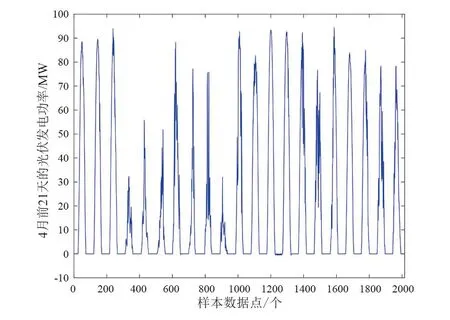
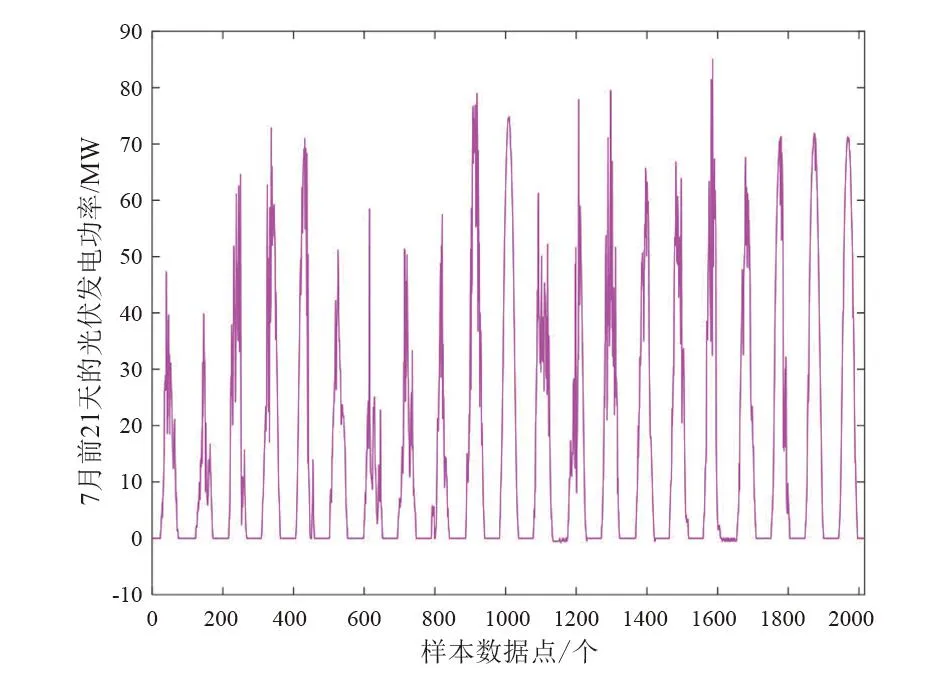
7)以均方误差作为适应度函数fcoot(·),如式(10)所示,分别计算白冠鸡跟随者个体xi,j的适应度函数fcoot(xi,j)的值和白冠鸡领导者个体xLD,k,j的适应度函数fcoot(xLD,k,j)的值。若fcoot(xi,j) (10) 式中:Nt为训练集样本数;ypv,t,i为光伏功率的预测值;ypv,a,i为光伏功率的实际值。 8)随机生成一个在[0,1]区间上的随机数R4,利用式(9)计算白冠鸡领导者的位置。 9)计算白冠鸡领导者的适应度函数fcoot(xLD,s,j)的值,若fcoot(xLD,s,j) 10)判断白冠鸡优化算法是否已达到最大迭代次数。如果已达到,那么输出支持向量机的最优参数;否则迭代次数加1,并跳至步骤3继续寻优。 COOT算法优化SVM参数的流程如图1所示。 图1 COOT算法优化SVM参数流程 以所建立的COOT-SVM短期光伏发电功率预测模型,选取某光伏电站在2017年春季中的4月前21天和夏季中的7月前21天的相关气象因素历史数据和光伏发电系统输出功率历史数据作为研究对象。4月1日至21日和7月1日至21日的光伏发电功率历史数据分别如图2和图3所示,所选取的数据按照每隔15 min采样一次的频率进行采集,采集时间范围为一整天,并分别选取4月22日和7月22日作为待预测日期,预测间隔为15 min,输出96个光伏发电功率预测数据。 图2 4月前21天的光伏发电功率 图3 7月前21天的光伏发电功率 为了避免数据之间因为不同量纲的差异而对预测结果造成影响,对所有输入和输出的数据都进行归一化处理,使数据都规整在[0,1]范围内,归一化的计算表达式[22-24]为 (11) 式中:T为原始数据;Tmin为原始数据最小值;Tmax为原始数据最大值。 通过白冠鸡优化算法优化SVM的惩罚因子和核函数参数可以获得COOT-SVM预测模型对光伏功率进行24 h的短期预测。为了进一步验证COOT-SVM预测模型的预测效果,通过与BP和SVM的预测结果进行比较,再通过仿真分析,可得某光伏电站在2017年春季中的4月22日和夏季中的7月22日的短期光伏发电功率的预测值和实际值,分别如图4和图5所示。 图4 4月短期光伏发电功率预测结果 图5 7月短期光伏发电功率预测结果 从图4、图5中可以看出,COOT-SVM 预测模型的预测值比BP和SVM预测模型更接近实际光伏功率的数值。 考虑多种误差对预测结果的影响,提高了预测结果的鲁棒性。这里采用3种误差指标对光伏功率预测结果进行评价,分别为均方根误差、均方误差以及平均绝对误差。 1) 均方根误差[25] (12) 式中:Treal(t)为t时刻实际的光伏发电功率;Tpred(t)为t时刻预测的光伏发电功率;m为预测样本数据的数量。 2) 均方误差[1] (13) 3) 平均绝对误差[26] (14) 使用BP、SVM和COOT-SVM模型对4月短期光伏发电功率进行的预测误差如表2所示。 表2 不同方法预测误差分析(4月) 从表2中可以计算出,COOT-SVM预测模型的TRMSE比BP和SVM预测模型分别降低了49.42%和38.80%;COOT-SVM预测模型的误差TMSE比BP和SVM预测模型分别降低了74.42%和62.54%;COOT-SVM预测模型的TMAE比BP和SVM预测模型分别降低了59.14%和44.41%。 使用BP、SVM和COOT-SVM模型对7月短期光伏发电功率进行预测的误差如表3所示。 表3 不同方法预测误差分析(7月) 从表3中可以计算出,COOT-SVM预测模型的TRMSE比BP和SVM预测模型分别降低了14.44%和24.03%;COOT-SVM预测模型的TMSE比BP和SVM预测模型分别降低了26.79%和42.29%;COOT-SVM预测模型的TMAE比BP和SVM预测模型分别降低了8.24%和41.63%。 对比结果表明,COOT-SVM预测模型比BP和SVM预测模型具有更好的预测精度和稳定性。 上面构建了一种COOT-SVM预测模型对短期光伏发电功率进行预测。通过皮尔逊相关系数公式可以计算得到对光伏发电影响较大的因素为太阳总辐射强度、太阳散射辐射强度、太阳直射辐射强度、组件温度和环境温度5个气象因素,将它们作为输入数据,光伏电站的发电功率作为输出数据,并对输入和输出的数据进行归一化处理;利用COOT-SVM预测模型实现光伏发电功率的短期预测。通过将由COOT-SVM预测模型与BP、SVM预测模型得到的预测功率的曲线和实际输出功率进行对比,并计算出BP、SVM和COOT-SVM预测模型的均方根误差、均方误差和平均绝对误差,可知COOT-SVM预测模型具有优越的预测性能和较高的稳定性,能够为短期光伏发电功率预测提供理论参考。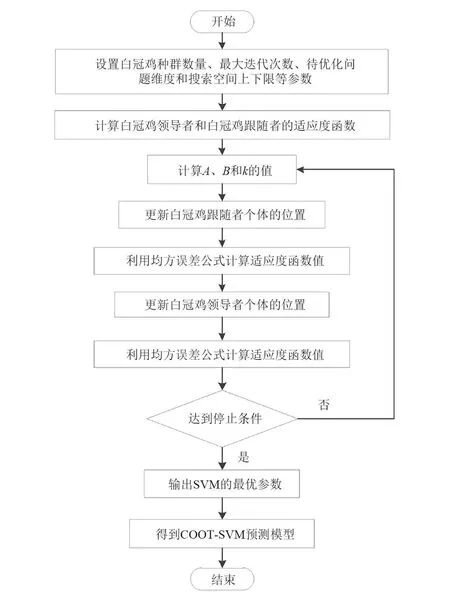
4 算例分析
4.1 短期光伏功率预测结果及其分析
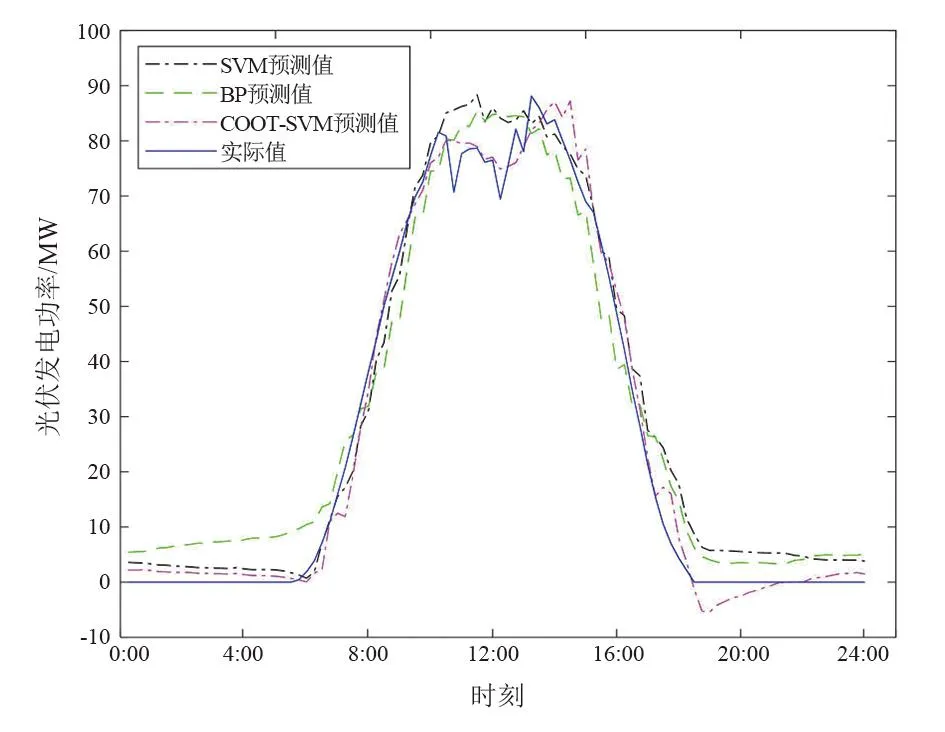
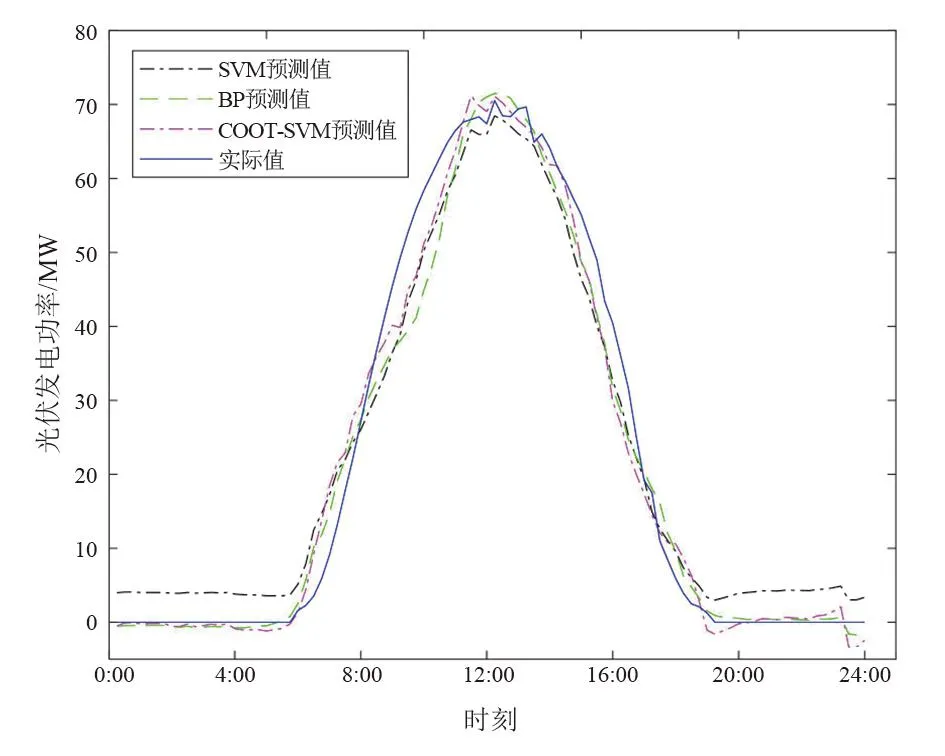
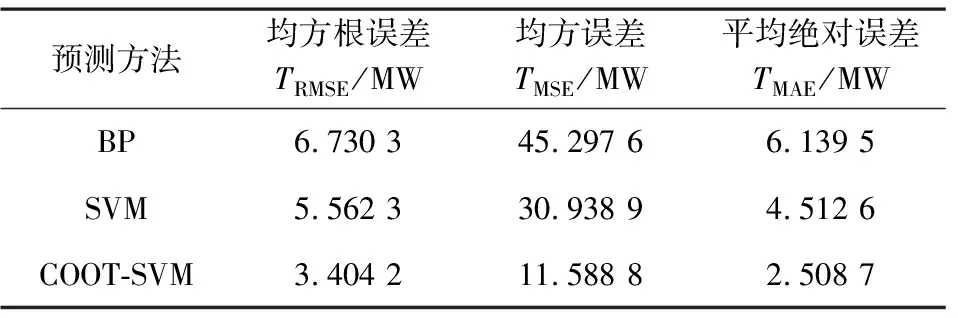
4.2 预测结果评价指标

5 结 论
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

