考虑热网潮流的区域热-电综合能源系统协同优化配置研究
邓靖微,曹敏琦,晁化伟 ,陈大为,胡 涛
(1. 国网四川省电力公司经济技术研究院, 四川 成都 610041;2. 湖南大学电气与信息工程学院,湖南 长沙 410082)
0 引 言
区域热-电综合能源系统(regionally integrated heat and electricity system, RIHES)作为连接用户与供能网络的终端,对于缓解当前环境保护与能源需求的矛盾具有重要意义[1]。RIHES利用能量转换设备耦合区域热网和配电网能够提高能源利用率。RIHES作为能量转换最复杂的环节,合理统筹其新增设备规划与系统运行策略,实现节能增效的同时兼顾投资经济性是一个值得关注的问题[2]。
目前,针对RIHES的协同优化配置已有较广泛的研究[3-9]。如文献[3]固定了待配置设备的容量,以设备是否安装的0-1变量作为规划决策变量,用随机优化方法求解RIHES的随机规划模型。文献[4-5]以设备容量作为规划决策变量,固定了待配置设备的数量,采用随机优化方法、区间优化等方法求解计及源荷不确定性因素的RIHES规划模型。文献[6-7]考虑经济性与可靠性双重因素,分别从引入可靠性指标校验经济性的单目标优化和可靠性与经济性双目标优化两个角度,讨论了双重目标下的RIHES优化配置问题。文献[8-9]从储能角度展开,通过精细化储能模型,考虑RIHES中储能装置的配置问题。上述文献从不同角度研究了RIHES的优化配置问题,但是,在设备配置方面均以待配置设备的容量[4-9]或数量[3,9]作为规划决策变量,并未考虑同类设备的容量及数量同时作为规划决策变量的设备配置策略。此外,在运行方面,上述文献均未考虑传输网络模型,而导致优化结果无法满足实际RIHES的网络传输损耗及传输变量对应的静态安全约束。
考虑传输网络模型后,规划决策变量还需考虑待配置设备的选址,即设备接入对应网络的节点位置;此外,原决策变量设备数量变为设备可接入节点的数量。现有考虑传输网络模型的RIHES协同优化配置的研究主要集中在用户侧综合能源系统[10-11]和多区域综合能源系统[12]。有研究初步考虑了传输网络模型,但其热-电传输网络模型仅包含外部母线功率平衡模型,并未对网络潮流进行精细建模[10]。文献[12]建立了热网潮流模型,针对各区域接入网络的设备容量进行优化配置,但并未考虑电网潮流模型。然而实际热网采用调节流量的量调节或调节温度的质调节运行方式[1],但上述研究中的热网模型并未考虑区域热网流量或温度的变化。因此,有研究进一步考虑了质调节运行下区域热网及储能模型,优化配置接入RIHES中的储能容量及接入节点位置[13],但由于储热装置难以用温度量化其充放热过程,因此采用控制储热装置等效水流量的运行方式改变储能的充放功率,导致储热与热网的运行方式不符。由此可以看到,在包含储热装置的RIHES规划问题中采用量调节运行方式下的热网模型能够统一二者的运行方式。然而量调节运行方式下热网的潮流模型变为非凸非线性,造成优化模型难以求解。常用的求解方法即为假定管道流向已知且在调度周期内不变,采用凸松弛方法结合商业求解器来求解[14-15],但流向固定的运行方式难以适用于部分管道流向通常不确定的多热源区域热网[16]。
综上所述,现有关于考虑传输网络模型的RIHES规划-运行联合优化的研究仍有部分不足,具体为:
1)鲜有针对区域级综合能源系统应用场景;
2)规划方面除了少量研究仅考虑设备定容,大部分将设备容量通常考虑为几类离散的已知量,仅规划其接入节点及设备选型的规划策略;
3) 运行方面热网模型与供热设备模型采用的运行方式不符及未考虑热网的管道流向可变因素。
基于上述考虑,提出了一种考虑流向可变的量调节运行方式下的RIHES的协同优化配置模型。首先,在运行方面建立了流向可变的量调节运行方式下的热网潮流模型;然后,对热网模型进行松弛,同时引入罚函数以收紧松弛间隙,进而将其转化为二阶锥规划模型。其次,在设备配置方面,同时考虑设备待配置容量及接入节点位置作为决策变量的设备配置策略建立规划模型。最后,结合其他设备及配电网的模型提出以设备配置与系统运行的经济性及新能源机组削减为目标的协同优化配置模型,并在IEEE 33节点配电网与17节点区域热网测试系统中求解。算例验证表明所提协同优化配置模型具有优越性,考虑流向可变的热网模型对设备配置经济性有积极的影响。
1 区域热-电综合能源系统模型
所建立的RIHES结构如图1所示,由热电联产(combined heat and power, CHP)、风力发电(wind turbine generation,WT)、光伏发电(photovoltaic power generation,PV)、电锅炉(electric boiler, EB)、蓄热式电锅炉 (electric boiler with thermal energy storage, EBTES)、蓄电装置(electrical energy storage, EES)及配电网、区域热网与电、热负荷组成。
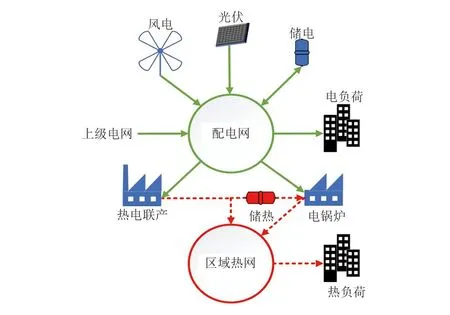
图1 区域热-电综合能源系统结构
1.1 区域热网凸松弛模型
1.1.1 考虑流向可变的水力模型
热网中各节点处与该节点相关支路的质量流量满足:
Amb,t=mq,t
(1)
(2)
式中:A为热网的供水网络的节点-支路关联矩阵;mb,t为t时段热网各管道的质量流列向量;mq,t为t时段热网各节点质量流列向量;aij为A阵中元素。
由于传输管道有一定的粗糙度,可由达西-魏斯巴赫(Darcy-Weisbach)公式计算。
hbj,t=Sjmbj,t|mbj,t|,∀j∈B
(3)
式中:Sj为管道j的比摩阻[17];B为管道集合。
考虑流向可变因素时,则需要预定义各管道的方向,式(1)中A阵中各元素按照预定义的方向选取,若所求得管道j在t时段的流量mbj,t为正,则表示管道实际流向与预定义的方向一致,反之亦然。建立式(4)模型表征管道流向及流量限制。
(4)
式中,mbj,min、mbj,max分别为管道集合B中管道j的流量最小值和最大值。
1.1.2 热力模型
φi,t=Cpmqi,t(TSi-TOi),∀i∈Q
(5)
(6)
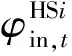
此外,热力模型还有热损耗模型及热力拓扑模型,详见文献[15]。
1.1.3 热网模型松弛
考虑管道流向后,去掉式(3)绝对值,松弛为分段二阶锥形式,同时引入中间二进制变量xbj,t将分段约束式线性化,同时采用麦考密克(McCormick)松弛[18]引入变量Zbj,t并令其满足:
Zbj,t=xbj,thbj,t,∀j∈B
(7)
则式(3)、式(4)变为:
-mbj,max(1-xbj,t)≤mbj,t≤mbj,maxxbj,t,∀j∈B
(8)
mbj,minxbj,t≤mbj,t≤-mbj,min(1-xbj,t),∀j∈B
(9)
xbj,thbj,min≤Zbj,t≤xbj,thbj,max,∀j∈B
(10)
hbj,t+(xbj,t-1)hbj,min≤Zbj,t≤hbj,t+
(xbj,t-1)hbj,max,∀j∈B
(11)
(12)
式(8)—式(11)均为线性约束,式(12)为二阶锥约束。
为保证松弛精确性,将管道压差作为惩罚目标函数。
(13)
式中,μh为管道压差惩罚因子。通过最小化惩罚项能够使二阶锥约束接近原等式约束,保证松弛的精确性。
1.2 蓄热式电锅炉模型
相比单一EB,EBTES不受热负荷需求限制,能够在热负荷需求低谷阶段将电能转化为热能,通过TES在时间尺度上平移至负荷需求高峰阶段供热,缺点是供热能量损耗较电锅炉直供方式下大。因此,采用EB与EBTES自由组合的配置方式,二者模型可统一描述如下。
1.2.1 电锅炉模型
(14)
(15)
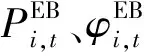
1.2.2 蓄热装置模型
不同于传统TES的充放热端口均与热网连接,仅可在热负荷低谷且供热设备供能过剩时期储存热网多余的热能,反之向热网放热,因而其储、放能不可同时发生。而EBTES中的TES由于储热功率来源于EB,无需满足上述限制,可实现利用EB储热的同时向热网放热,并在一段时间内与EB同时供热以提高供热上限。

(16)
(17)

1.3 其他模型
其他模型包括配电网潮流模型、热电联产机组模型及电储能运行模型。配电网模型采用二阶锥形式的Distflow潮流模型,EES模型见文献[14],CHP模型见文献[19]。
2 协同优化配置模型
2.1 规划策略
基于第1章所建立的RIHES模型建立协同优化配置模型。模型中决策变量由设备规划变量和系统运行变量两部分组成。规划变量包含待配置设备的容量及接入网络的节点位置。考虑到实际中CHP机组占地面积较其他各类设备大,受场地环境等因素影响,CHP机组无法随意确定安装节点位置。此外,随着碳排放政策的限制,中国各地“十四五”能源规划均以分布式新能源和储能规划为主[20],合理协调传统化石机组与其他新建供能设备的容量以达到协同节能降效的效果具有一定现实意义。因此固定CHP机组接入节点及数量,仅考虑将配置容量作为规划变量,而WT、PV、EB/EBTES等其他设备同时考虑能否接入节点的0-1变量及待配置容量的连续变量作为规划决策变量。运行变量为典型日中各时段内各设备出力、热网的管道质量流量及节点注入流量、电网潮流相关变量等。
2.2 目标函数
综合考虑RIHES的投资及建设的经济性和新能源机组消纳,以待配置设备的年投资成本Cinv、年运行成本Cop和新能源机组的年出力削减Ccur最小为优化目标,其表达式为
minC=Cinv+Cop+Ccur
(18)
2.2.1 年投资成本
(19)

2.2.2 年运行成本
Cop=θd·(FCHP+Fe+Fh)
(20)
(21)
(22)
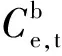
2.2.3 新能源机组年出力削减
Ccur=θd·(FWTc+FPVc)
(23)
(24)
(25)

2.3 约束条件
2.3.1 规划约束
1)设备容量及节点规划约束
对于WT、PV、EB等同时考虑节点位置及配置容量的设备,规划变量需满足如下约束:

(26)
(27)
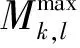
此外,考虑场地限制等因素,在单个节点上配置的供能机组不能超过一台。

(28)
2)CHP机组规划约束
(29)
2.3.2 运行约束
1)WT、PV约束
(30)
(31)
(32)
(33)

2)储能约束
对于电、热储能设备,典型日内任意时段运行变量与规划变量需满足如下约束:
(34)
(35)
(36)
(37)
(38)
(39)
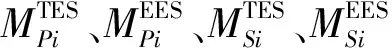
2.4 求解方法
上面提出的热-电综合能源系统协同优化配置模型为混合整数二阶锥规划模型(mixed-integer second-order cone programming, MISOCP),可利用商业求解器Gurobi 9.1.1建模并求解。
3 算例分析
3.1 输入数据
采用改进的IEEE 33节点配电网和17节点区域热网测试系统[21],系统网络结构如图2所示。电网基准电压为12.66 kV,电网基准容量为100 MW,上级电网通过节点1与配电网连接,上级电网交互功率上限为20 MW;区域热网测试系统包含17个热网节点及16条热力管道,基准容量为150 MW,各管道预定义流量方向如图2区域热网中各支路箭头所示,其中空心节点代表该节点无热负荷,实心节点则表明该节点有热负荷,CHP机组分别位于电网节点18和热网节点1处。
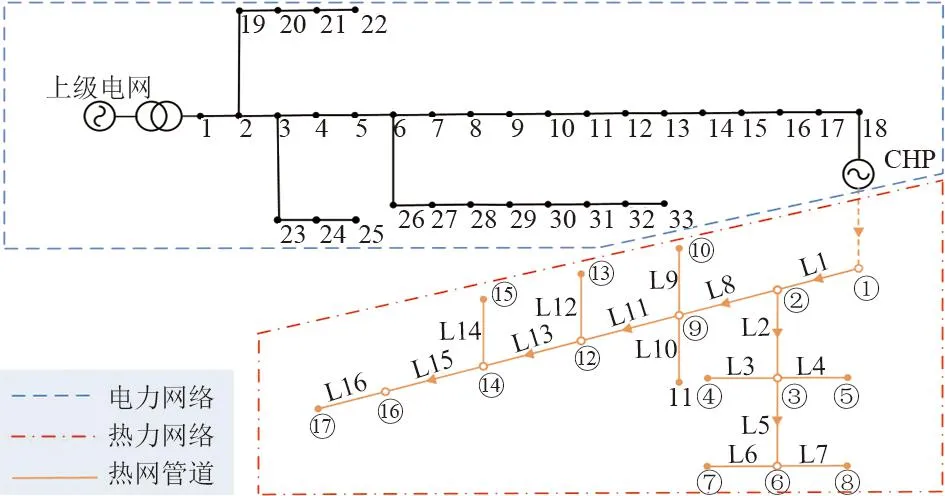
图2 系统网络结构
待配置设备的相关参数见表1,表中e表示对应设备配置在配电网中的节点位置;h表示对应设备配置在区域热网中的节点位置,其中TES和EES除了可安装储存容量上限外还有充放功率上限。
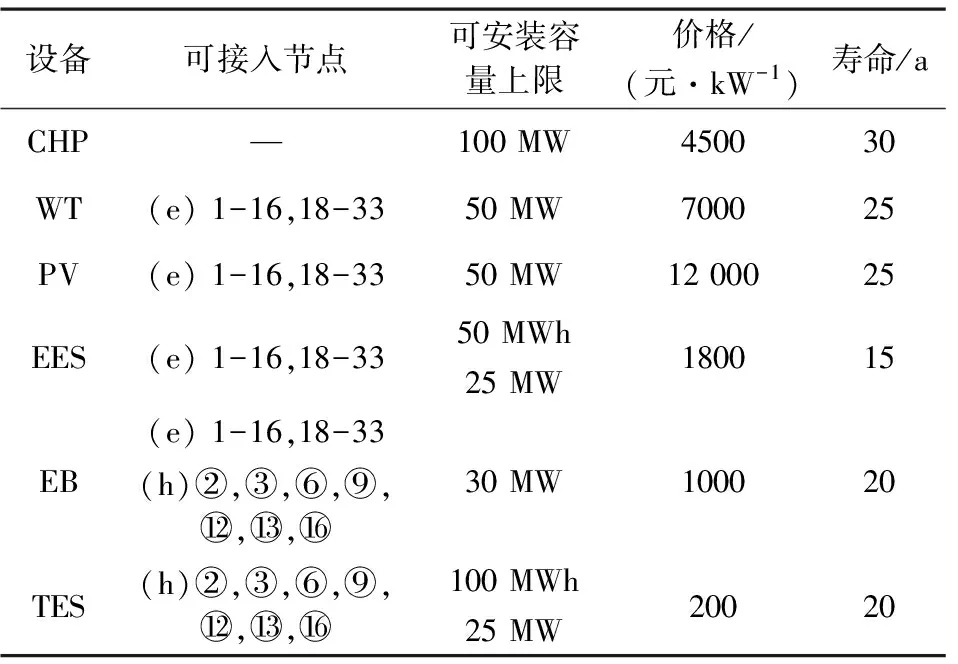
表1 设备配置参数
风力发电与光伏发电的预测值采用文献[4]中的确定性预测数据,风力及光伏机组惩罚系数取0.05,热网的松弛惩罚系数取0.04,进水温度为70 ℃,回水温度为40 ℃,热水比热为4.182 kJ/(kg·℃)。
3.2 优化配置结果分析
为验证所提的协同配置策略及热网运行模型的有效性,分别设置以下3种场景:
1)场景1:同时考虑设备配置容量及节点位置作为规划决策变量,热网运行决策变量中管道流向可变。
2) 场景2:采用传统规划策略,仅以设备是否接入节点作为规划决策变量,运行决策变量中管道的流向可变。
3)场景3:同时考虑设备配置容量及节点位置作为规划决策变量,但热网运行决策变量中管道流向固定不变,以所提预定义流量方向作为固定的管道流向。
3种场景下的设备配置结果见表2。场景1和场景3中CHP机组的配置容量基本一致而比场景2少9.89 MW;3个场景中WT配置容量及数量均相同,但各场景下配置的节点位置不同;场景2中其他设备配置的总容量均大于场景1和场景3;而场景1配置的PV总容量较场景3少1 MW;至于EES,场景1则比场景3多配置了3.5 MW;3个场景在区域热网中均采用两台EB及一台EBTES的组合配置方式,而场景1中EB和TES配置的总容量分别比场景3少1.66 MW和0.91 MW。各场景下成本明细见表3。场景1的年规划成本和运行成本比场景2和场景3低,但新能源机组削减成本略高于场景3,由于场景2中PV的配置容量较大导致新能源机组的削减成本远高于其他两个场景。综合之下,场景1的总成本最低,场景3的总成本略有增高,而场景2的总成本与其他两个场景下的总成本的差异较大。

表2 不同场景下设备配置结果
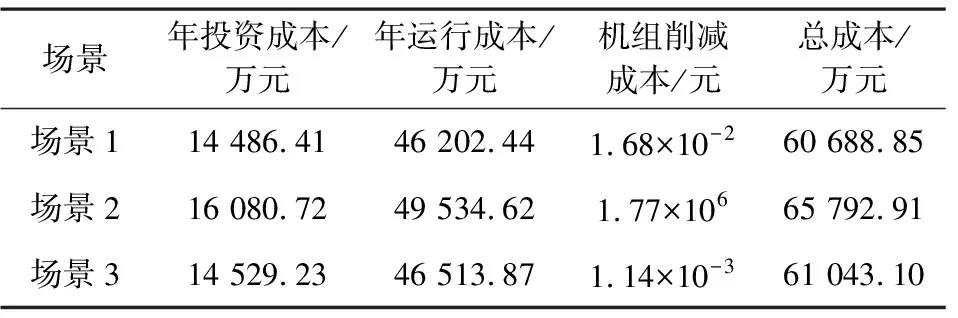
表3 不同场景下的成本明细
图3为各设备供电、供热结构图。由图3(a)可以看到场景2中购电比例为5.32%,少于场景1和场景3的12.39%,这部分购电功率由其他供电设备替代;场景2中EES的出力比例为9.24%,大于场景1的5.37%和场景3的5.71%。图3(b)中场景2的TES供热比例为4.69%,大于场景1的1.59%和场景3的1.57%。尽管场景1与场景3各设备的出力比例接近,但场景3中总供电量和供热量较场景1分别多出0.34 GWh和0.12 GWh。

图3 各场景下供能结构
3.3 规划策略对协同运行的影响
对比分析不同规划策略下的场景1与场景2中典型日的运行结果以验证不同规划策略对RIHES协同运行经济性的影响。两场景下CHP及PV的电出力如图4、图5所示。由图4看到场景2下从上级电网购电的供能比例降低,这部分功率主要由CHP和PV承担。由于场景2中EES配置容量过大及其供能增加,导致其他电源不得不增加出力为EES储能,进而使得场景2下的设备总出力较大。尽管图5中场景2的PV供能比例与场景1接近,但由于场景2下PV配置容量较场景1大,因此在运行周期内PV的实际出力比场景1多24.26 MW,而CHP的出力比场景1多283.65 MW。
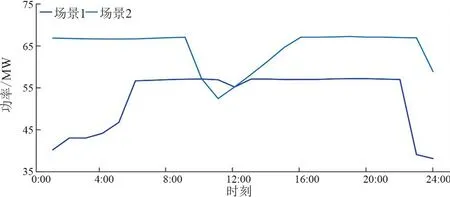
图4 场景1和场景2下CHP机组电出力

图5 场景1和场景2下PV出力
图6为两场景下各供热设备出力。场景2中TES同样由于配置容量较大比场景1多储热62.5 MW;但其EB及EBTES向区域热网的实际总供热功率比场景1少了6.99 MW,因此场景2中CHP热出力比场景1多6.99 MW以补充这部分功率缺额。
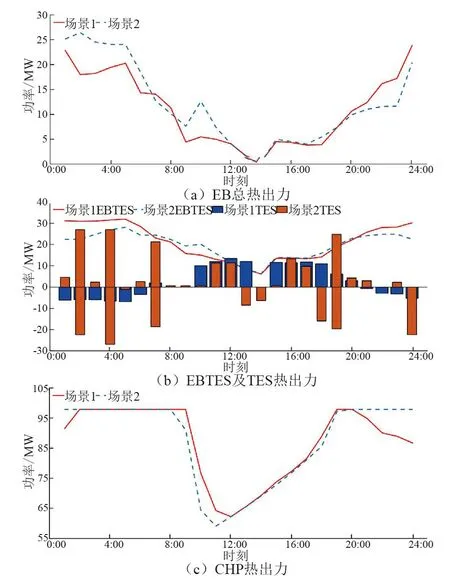
图6 场景1和场景2下供热设备热出力
综上,由于场景2配置容量固定策略下设备配置容量较大,为了提高设备利用效率,一方面外购电能供能降低以提高配置的供能设备的出力;另一方面供能设备额外增加出力向储能装置充能,导致了场景2的运行成本增加。
3.4 热网管道流向对协同运行的影响
对比分析管道流向可变的场景1与管道流向固定的场景3,验证管道流向对RIHES协同运行经济性的影响。由于场景3中管道流向固定,导致两场景中优化结果管道流量不同。以流量差别最大的管道L15为例,两场景中该管道流量如图7所示,场景1中流量正负交替,表明场景1下该管道的流向在调度周期内发生了两次变化;而场景3中流向固定不变,导致部分时间流量较小,两场景均在区域热网节点处配置有EB,场景3中节点处的EB受到管道流量限制,仅能向节点处热负荷供能。因此在该结点处EB的配置容量较小,转而增加了在节点③处的EB配置容量。两场景的购电功率见图8,场景3比场景1多购电1.07 MW。
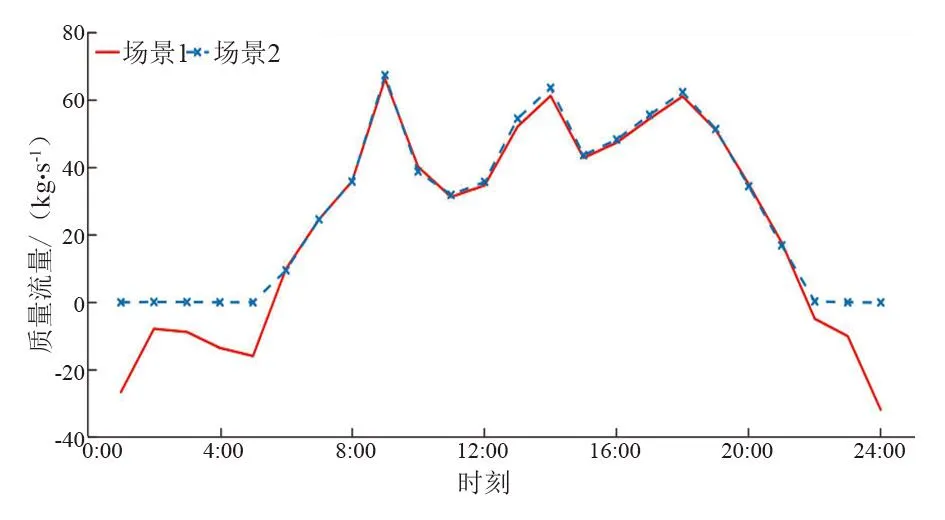
图7 场景1和场景3下管道L15的流量

图8 场景1和场景3下购电功率
场景1中在管道L15处的流量为负的对应时刻即为EB通过管道L15向其他热负荷传输热能。两场景下节点处EB注入功率如图9(a) 所示,场景1中节点处EB供能比场景3多16.12 MW,这部分热功率在场景3中由配置在节点③处EB和CHP机组提供;图9(b)、(c)为两场景下EB和EBTES总供热功率及CHP机组供热功率。与场景1相比,场景3中EB和EBTES的总供热功率比场景1少1.05 MW,而CHP增加出力替代这部分功率。由于流量限制进一步导致了CHP机组出力的增加和外购电功率的增加使得场景3的运行成本略高于场景1。
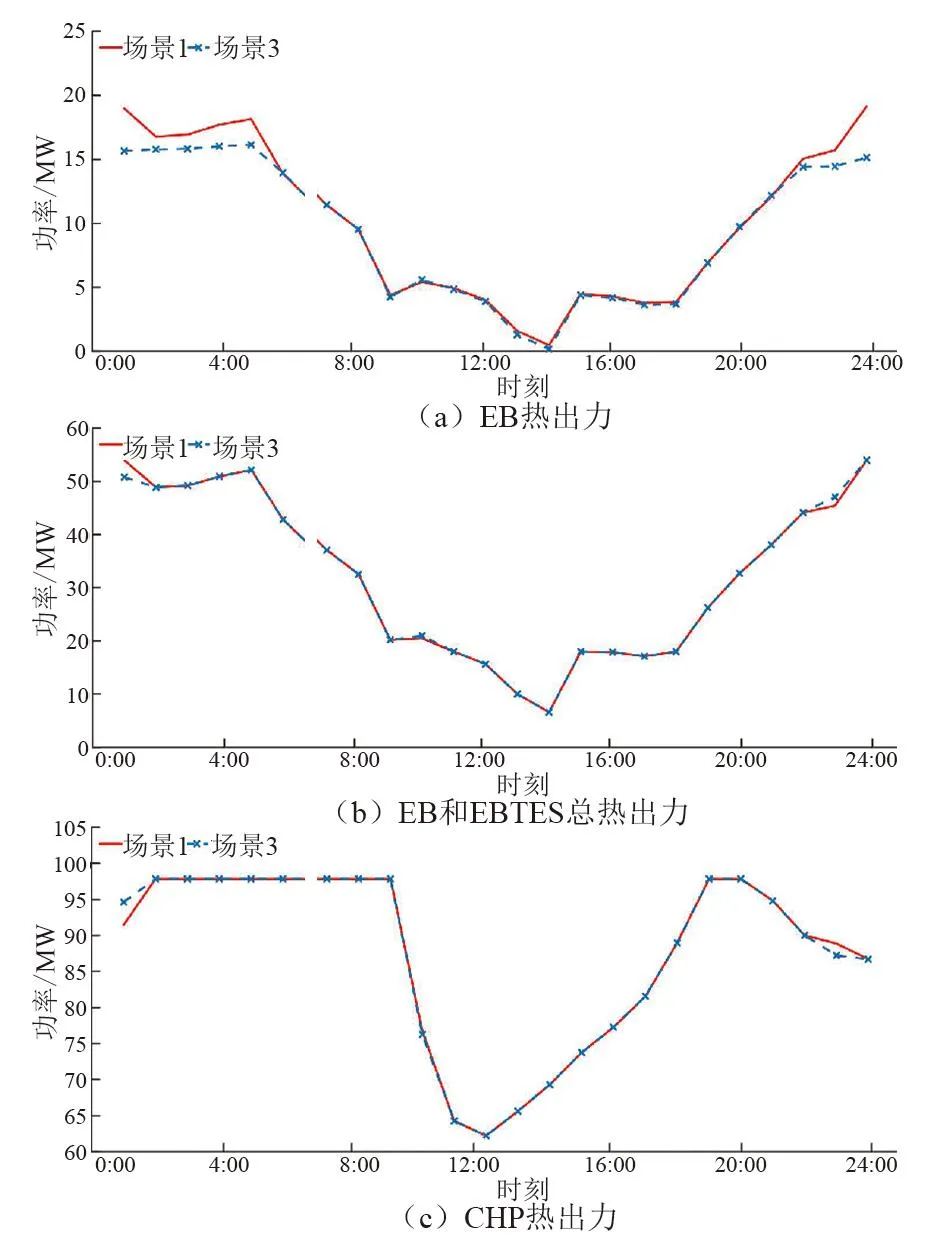
图9 场景1和场景3下供热设备热出力
4 结 论
上面建立了考虑流向可变量调节运行方式下的热网模型,通过松弛结合罚函数的方式将其转化为二阶锥形式。进一步结合其他设备及电网潮流模型,在传统经济性目标的基础上考虑新能源机组消纳目标,建立了规划-运行联合优化模型(混合整数二阶锥规划模型),该模型下的规划策略能够同时优化多种设备接入节点的位置及其配置容量。通过算例验证,得出以下结论:
1)同时考虑设备配置容量及节点位置的规划策略能够有效降低规划成本,并且能够避免部分容量配置冗余的供能设备增加出力与储能装置进行多余的能量转换,具有更好的经济性。
2)流向可变的区域热网模型在提高RIHES的经济性和运行灵活性方面具有优势。通过仅改变局部管道的流向进而在就近节点负荷需求较低时将热能传输给更多热负荷,增加供热机组的灵活性,能够得到更经济的设备配置方案及运行方案。

