考虑控制模式影响的多电压等级直流电网潮流计算方法

叶 希,陈 振,朱 童,张英敏,李保宏

(1.国网四川省电力公司,四川 成都 610041;2.国网四川省电力公司电力科学研究院,四川 成都 610041;3.四川大学电气工程学院,四川 成都 610025)

0 引 言

近年来国际能源供求形势紧张、气候环境不断向不利于人类生存的方向转变[1-2],这使得优化现有能源结构,实现能源结构多元化意义重大[3-4]。据统计,截止到2022年年底,中国已有发电装机容量大致为2560 GW,风电约占14.45%,光伏约占15.23%。展望未来,伴随着可再生能源成本降低以及配套储能技术的进步和成熟,可再生能源装机有望保持较快增长势头[5]。安全、可靠、经济的电能传输通道是可再生能源规模化发展、远距离输送和消纳的关键。但交流电力系统稳定性等问题随着输送容量和距离的增加变得更加复杂。而基于先进的直流输电技术建立主干电网[6],在远距离、大容量电能输送方面优势明显。

潮流分布在规划电力系统未来扩展方面扮演着关键的角色[7-8]。通过分析潮流分布可以确定潮流集中的区域和负载高峰期,从而合理调整电力系统的组成部分,有效提升系统的输电能力和供电可靠性。此外,潮流分布分析还可以揭示系统中可能存在的瓶颈和薄弱环节,为改进和升级电力设备提供指导。对潮流分布进行深入研究和分析,有助于有效评估电力系统的负载需求、优化系统配置,并制定可持续发展的电力规划策略[9-12]。

现有潮流计算方法大多以迭代法为核心[13],考虑直流系统的状态变量和控制变量进行迭代求解。文献[14]将潮流分布分解为定电压节点和定功率节点的叠加,通过灵敏度分析,实现了直流电网潮流分布的线性表达。文献[15]提出了一种新的潮流计算表达式,该表达式仅需改变式中的系数即可进行控制方式的转换,具有高效性。文献[16]提出了在下垂控制下,模块化多电平多端直流系统的潮流计算方法,但未指明在扰动及故障时潮流的变化规律。文献[17]在直流电网的稳态潮流计算中引入了基于节点阻抗矩阵的G-S法,能够提高计算精度,收敛性较好。文献[18]建立了电压控制模型,并考虑了换流站损耗对潮流计算的影响。文献[19] 提出了针对不同控制方式的潮流计算方法,并推导了在不同控制方式下计算雅可比矩阵和网络参数的方法,该方法适用性较广。但是目前计及直流变压器的多电压等级下直流电网潮流计算较少,在多电压等级直流电网中,不同电压等级的直流系统通过直流变压器相连,探究不同控制方式下的直流变压器损耗和通过的潮流对建立含多个电压等级的直流电网的潮流计算方法有重要意义。

下面首先基于直流变压器、换流站的控制方式,对多电压等级直流电网分区处理,建立了多电压等级直流电网稳态等值模型;然后,在对直流电网节点进行定义和分类的基础上,基于牛顿迭代法建立节点导纳矩阵及潮流方程,推导了直流电网潮流计算方法;最后,基于PSCAD仿真软件,搭建一个三电压等级13端柔性直流电网模型,验证了所提计算方法的有效性和正确性。

1 多电压等级直流电网稳态等值模型

1.1 换流站和直流系统的稳态等值模型

换流站的等值模型主要包括基于开关函数的数学模型、换流站交直流功率交换规律及控制器模型。模块化多电平换流器(modular multilevel converter,MMC)在工作时是子模块的不断投切实现功率传输,从子模块的投切状态来研究MMC的开关数学模型。换流器控制方法是实现交直流功率交换的重要保障,电压源型换流器的控制方法主要有间接电流控制方法、直接电流控制方法。其中间接电流控制过程相对简单,主要应用于早期的电压源型换流器(voltage sourse converter,VSC)直流输电技术中,但由于缺乏电流反馈环节,其动态响应时间较长,系统参数变化对控制稳定性的影响较大。在基于MMC的直流输电技术中,采用dq坐标系、PI控制算法的直流电流控制方法受到广泛使用。有功类外环控制器主要有定有功功率控制、定直流电压控制、定交流频率控制。

在数学模型和控制器设计的研究中,设注入到MMC的有功功率P等于直流侧功率Pdc和损耗Ploss之和

P=Pdc+Ploss

(1)

换流站损耗Ploss与传输功率Pdc间的关系可表征[20]为

(2)

式中,a、b、c为损耗系数。

从稳态潮流计算的角度看,直流系统可以忽略线路中的电感、电容等参数,仅考虑电阻参数即可。基于图论的方法,假定换流站i注入直流系统的电流为Idi,换流站i直流出口处电压为Udi,将换流站直流侧出口类比交流系统中发电机节点,即换流站i、换流站j等效为节点i、节点j,且节点i与节点j间的线路电阻用rij表示,节点i与节点j间的线路电导用Gij表示;基于电路原理中的基尔霍夫定律,换流站节点电压Udi和节点注入电流Idi间的关系为

(3)

式中,q为直流电网节点数。

节点导纳矩阵G的元素定义为

(4)

1.2 DC/DC稳态模型及多电压等级直流电网分区方法

重点研究用于高压大功率直流电网DC/DC变换器的稳态等值模型。在多电压等级直流电网中为了具备一定的阻断直流故障能力,往往采用如图1所示的MMC两端口隔离型DC/DC变换器拓扑结构。

图1 基于MMC的隔离型DC/DC拓扑结构

为保证功率的有效传输,这种MMC隔离型直流变压器必须有一侧采用定交流系统频率f与交流系统电压v控制方式(以下简称VF控制),以建立稳定的交流电压;另一侧的d轴控制可采用定直流电压控制、定有功功率控制或下垂控制等。因而该类型直流变压器一般有3种控制模式,分别为:1)VF控制/定直流电压控制;2)VF控制/定有功功率控制;3)VF控制/下垂控制。

直流电网中DC/DC稳态模型主要考虑其损耗的等值。由于该类型变压器与换流器相似,采用拟合方法可得到直流变压器损耗与输送功率的函数关系式。

在PSCAD中对13端系统进行仿真采样,记录所有直流变压器低压侧和高压侧的功率,求差即为换流站和直流变压器的损耗。这里仿真10次数据,利用Matlab中的拟合模块curve fitting进行拟合。变压器定功率值作为自变量,损耗值为因变量。

直流变压器的拟合以DC/DC1为例,其二次拟合结果为f(x)=p1·x2+p2·x+p3,x为变量,此处为运行功率。设定:p1=5.953e-0.5,p2=-0.022 15,p3=4.605,拟合结果如图2所示。

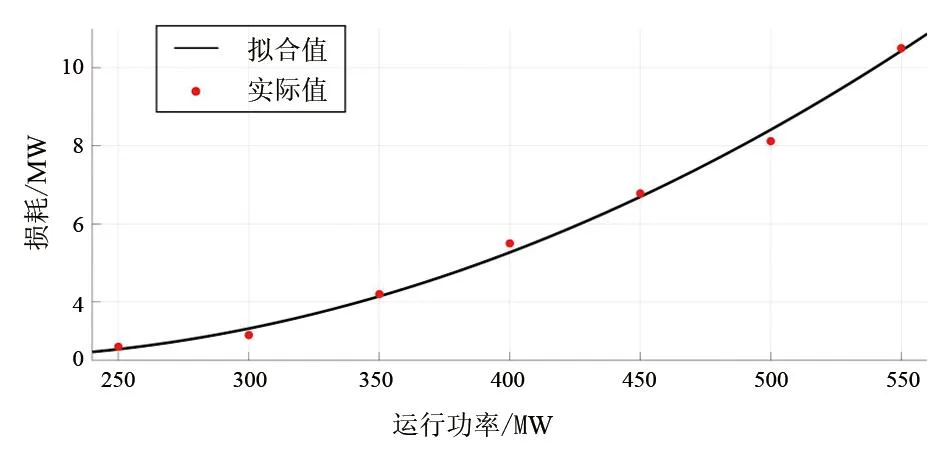
图2 直流变压器DC/DC1二次拟合化

图3 直流变压器等效模型

表1对损耗拟合结果进行了量化分析,结果表明所提方法误差均在3%以下,具有较高的准确度。

表1 拟合误差

其中,假定直流变压器m侧为VF控制,n侧为定有功率控制、定电压控制或下垂控制中的一种。由于VF控制方式是以交流侧频率、交流电压为控制对象,对直流侧有功功率或直流电压无控制能力,考虑直流变压器内部损耗,两侧的功率Pn、Pm为

Pn=Pm+Ploss

(5)

将变压器损耗公式代入式(5)得

(6)

故可将直流变压器可等效为一换流站。

直流变压器位于电网中独立母线节点或与换流站并联于同一母线节点。当位于独立母线节点时,直流变压器等效为换流站k1,控制方式取决于n侧控制方式,如图4所示。

图4 直流变压器接入独立母线节点

当n侧与换流站a并联于同一母线节点,直流变压器与换流站a可共同等效为一个换流站k2,控制方式取决于n侧换流站与换流站a,如图5所示。

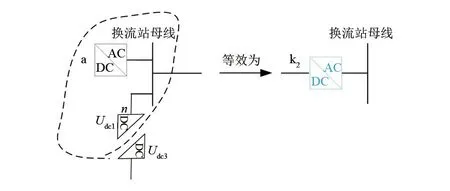
图5 直流变压器接入换流站母线节点

直流变压器m侧换流站控制方式主要分为表2的9种情况。

表2 换流站控制方式

以图6为例,由于直流变压器两侧功率Pn、Pm存在如式(5)所示关系,故按电压等级将多电压等级直流电网分区考虑,可将区域1的潮流计算结果代入区域2、区域3进行相关的潮流计算。

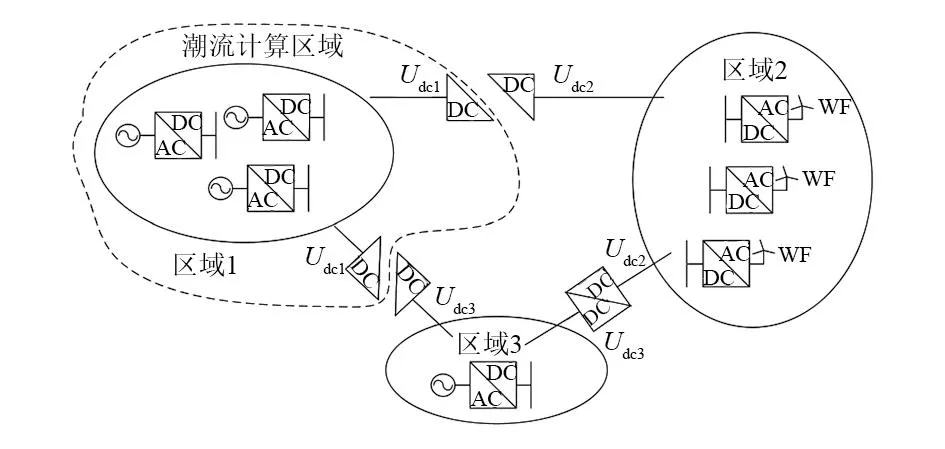
图6 潮流计算区域

2 多电压等级直流电网潮流计算模型

2.1 直流电网节点定义及分类

在直流电网中,每条直流母线同样可看作一个节点。然而,为所连接母线提供电压和注入功率的MMC换流器可独立控制其注入有功功率和无功功率,这是完全有别于交流系统的特征之一。类似交流系统潮流计算将节点划分PQ节点、PV节点和Vθ节点,根据MMC的不同控制方式,可将直流电网中的节点分为3类,以便用不同的潮流方程。即直流节点分为3类:类型Ⅰ为定交流有功功率和定直流功率节点,该类节点维持P跟踪参考值;类型Ⅱ为定直流电压节点,该类节点直流电压Ud始终恒定;类型Ⅲ为下垂控制节点,该类节点保持Pd和Ud满足特定斜率关系。

直流电网的协调控制主要体现为各换流站有功功率控制的相互配合,以此保证系统功率平衡和直流电压稳定。直流电网内至少需包含1个功率控制类(Ⅰ类或Ⅲ类)节点,且最多有1个直流电压控制类(Ⅱ类)节点。

目前采用较为广泛的两种协调控制方式是主从运行方式和下垂运行方式。

2.2 节点导纳矩阵及潮流方程

直流电网中,接入的储能单元也可看作电源或负荷,如光伏列阵经过DC/DC接入,可视为直流电源。与直流负载或电源直接相连的节点处理为恒功率节点,其功率修正方程为

(7)

式中:ΔPdi为i节点直流功率不平衡量;λ为与直流负载或电源直接相连的节点数;PdcLi为i节点直流负载或电源的直流功率。

与直流负载或电源非直接相连节点中,与MMC非直接相连的中间直流节点功率修正方程为

(8)

式中,γ为与直流负载或电源非直接相连的中间节点数。

可采用牛顿-拉夫逊法对上述非线性方程进行迭代求解。直流电网潮流修正方程为:

ΔPd=JdcΔUd

(9)

(10)

式中:ΔPd为直流节点功率增量向量;ΔUd为直流节点功率增量向量;Jdc为直流电网雅克比矩阵;k为迭代次数。

采用主从控制时,从换流站节点功率修正方程为

(11)

式中,η为从换流站节点数。

当采用下垂控制时,节点功率修正方程为

ΔPd=Pd+Ploss-Pdref+K(Ud-Udref)

(12)

式中:Pdref为有功功率参考值;Udref为直流电压参考值;K为下垂控制系统下垂系数。

将式(11)—式(12)中的p个多元函数在初始值附近分别展开成泰勒级数,并略去ΔU的二次及以上阶次的各项便得到:

(13)

将式(13)写成矩阵形式就如式(9)所示,其中雅可比矩阵Jdc如式(14)所示。

(14)

雅可比矩阵各元素定义为

(15)

式中,Jdcxy为Jdc中第x行第y列的元素。

定直流电压的主换流站是功率平衡站,直流电压恒定,不需要加入迭代中,故而雅可比矩阵Jdc需要降一阶,将对应定直流电压站节点的行列元素删去。

当采用下垂控制时,对应雅可比矩阵各元素定义如下:

(16)

2.3 直流电网的潮流计算方法

这里只研究基于牛顿迭代法潮流计算方法的流程框图,如图7所示。

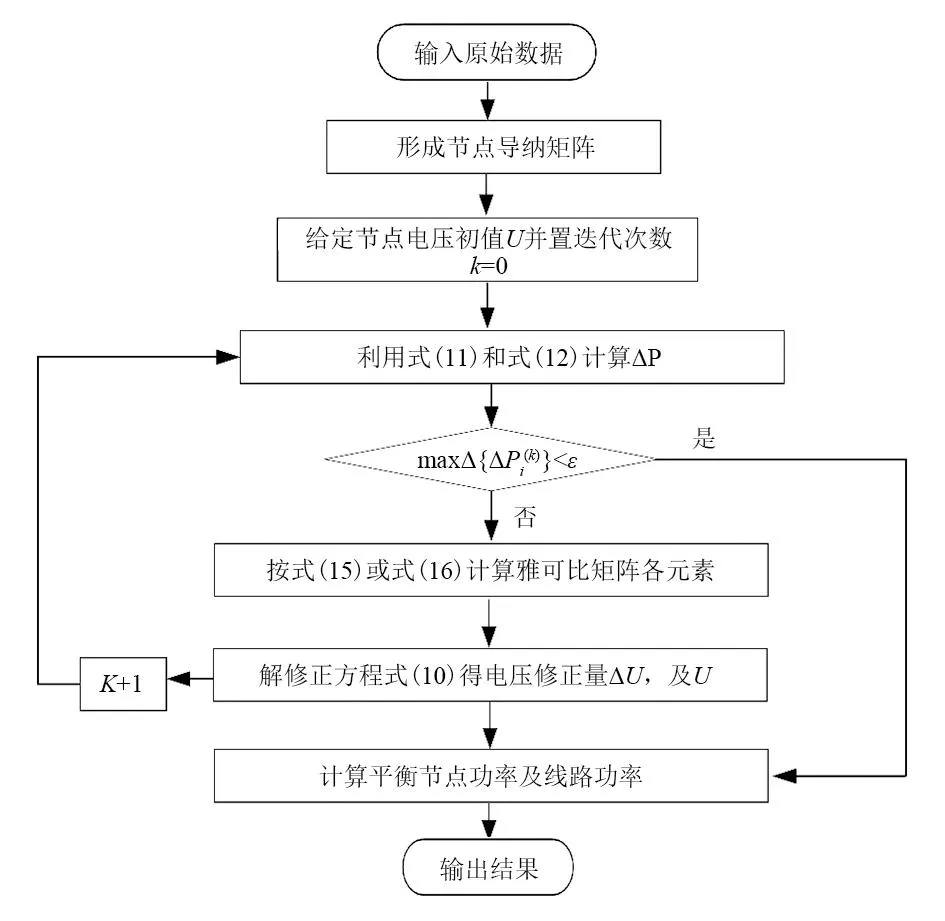
图7 牛顿法潮流计算程序

计算过程为:

1)输入系统原始数据。

2)将多电压等级直流电网分区,构建分区节点导纳矩阵;设定节点电压初值。

3)计算功率修正方程不平衡量ΔPd。

4)判断相应变量是否达到收敛要求:是,则输出结果,计算结束;否,则继续执行下一步。

5)计算迭代雅克比矩阵Jdc及电压修正量ΔUd。

6)返回步骤3,继续进行计算。

3 仿真验证

为了验证上述多电压等级直流电网潮流计算方法的正确性,现基于PSCAD仿真软件,搭建一个三电压等级13端柔性直流电网模型,如图8所示。其中各换流站的控制参数如表3所示,直流变压器的控制参数如表4所示。

表3 换流站控制参数

表4 直流变压器控制方式

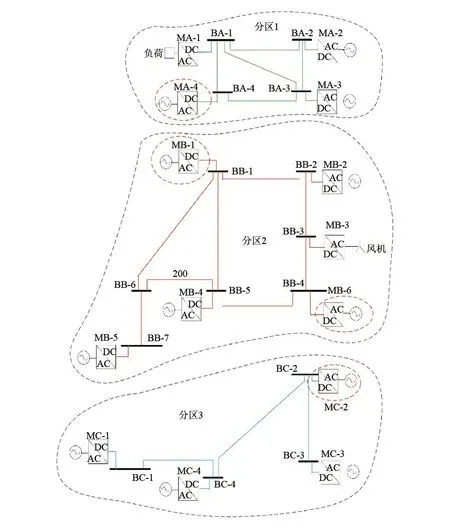
图8 13端多电压等级直流电网拓扑结构及计算分区模型

根据多电压等级直流电网分区方法,将图8划分为3个分区,如图8中虚框所示。根据与直流变压器相连的换流站节点等效方法,换流站MA-4、MB-1、MC-2与直流变压器直接相连,DC/DC2高压侧与独立母线BB-4相连,对应的等效换流站的控制方式及参数如表5所示。

表5 等效换流站节点控制参数

表5中:a1、b1、c1和a2、b2、c2分别为直流变压器DC/DC1和DC/DC2损耗系数;UdA-4为潮流计算中节点BA-4的直流电压迭代结果。

该潮流计算方法线路潮流计算结果与PSCAD仿真值的对比如表6所示。从表6可看出,线路潮流计算结果与仿真值的差值均在1%以内。产生误差的主要原因是换流器、直流变压器器的损耗由拟合函数求得,与实际损耗存在一定的误差;次要原因是牛顿迭代法存在固有的截断误差。但计算结果与仿真值可观的吻合度验证了所提多电压等级直流电网潮流计算方法的正确性。

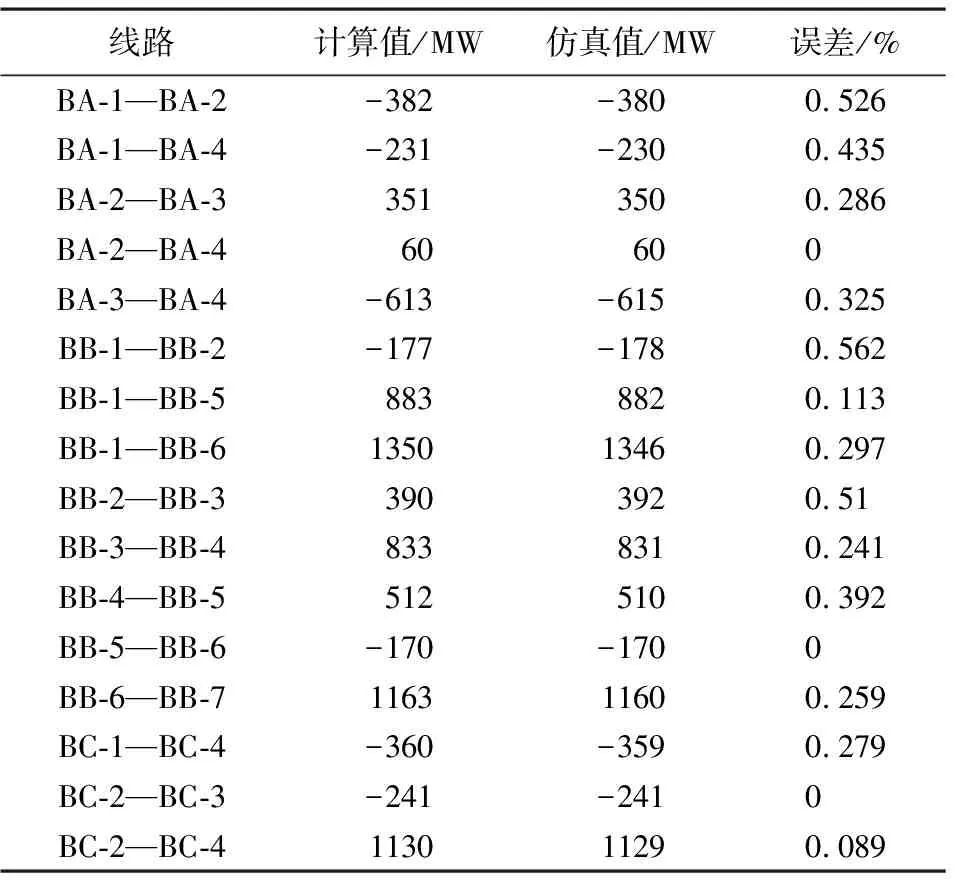
表6 线路的潮流计算结果与仿真值对比

4 结 论

上面研究基于MMC的多端直流电网潮流计算问题,主要内容包含以下两个方面:

1)基于直流变压器、换流站的控制方式,对多电压等级直流电网分区处理,建立了多电压等级直流电网稳态等值模型;

2)根据所提多电压等级直流电网分区方法,基于牛顿迭代法建立节点导纳矩阵及潮流方程,推导了直流电网潮流计算方法,并在13端直流电网上验证了所提方法的正确性。