基于改进相关系数的犹豫模糊集聚类分析

范玉蕊， 王惠文

（云南师范大学 数学学院，云南 昆明 650500）

在处理模糊不确定性的问题时，模糊集理论显示出其优越性和有效性。在日常的经济生产活动中，遇到决策者在几个数值间徘徊的情况时，直觉模糊集不能够进行精确描述。为了解决这个问题，Torra[1]将犹豫这一概念融入到模糊集理论中，并给出犹豫模糊集的概念，用于反映出决策者的犹豫情况。之后，Chen等[2]又提出了区间值犹豫模糊集，用区间数来表示隶属度情况。在此基础上，文献[3-4]研究了其相关性质和基本运算。

相关系数一直是模糊理论中的重要研究对象，在聚类分析中有着广泛的应用。2013年，Chen等[2]定义了犹豫模糊集的相关性度量，并讨论了相关性质，但是默认犹豫模糊元具有相同的长度，其值按递增顺序排列；次年将相应公式推广到区间值犹豫模糊集上。2015年，Liao等[5]提出犹豫模糊集的相关系数也应具有一定的犹豫性，在一定的区间内并非是一个准确的数。2018年，Guan等[6]提出综合相关系数，从均值、方差、长度3个角度综合考量，克服了之前要求对应犹豫模糊元具有相同长度的局限性，但是覆盖了一定的内部信息。2019年，Yang等[7]提出的相关系数公式同样不要求对应犹豫模糊元长度相等，但是存在的特殊情况（分母为0）没有被考虑在内。另外，文献[8-12]细节性地阐述了相关系数在聚类分析中的应用，文献[13-14]展示了2种其他类型的相关系数。本文继承了Yang等人的思想，并对其进行补充，提出带有犹豫度的犹豫模糊集相关系数计算公式，并推广到区间值犹豫模糊集上，最后证明其良好性质，并应用于数值算例说明其合理性和有效性。

1 基本概念

2 改进的犹豫模糊集相关系数及算例分析

2.1 改进的犹豫模糊集相关系数

定义7 考虑到各属性权重不同以及决策者对犹豫模糊集隶属度差异部分和犹豫度差异部分的偏好程度不同，定义相关系数公式为

其中，

α,β≥0且α+β= 1。ρWHFSX1(A,B)和ρWHFSX2(A,B)分别代表犹豫模糊集隶属度部分的相关性和犹豫度部分的相关性。

为保证其普适性，需要考虑分母为0的特殊情况，即2个犹豫模糊集中各个属性对应元中的隶属度值的个数都为1或其中一个为1的两种特殊情况。当属性相对应的两个犹豫模糊元中数值个数都为1时，则规定在犹豫度部分其相关性为1；当各个属性对应元hA(xi)中的数值个数都为1，在hB(xi)中其数值个数不都为1时，其犹豫度部分的相关系数定义如下：

当各个属性对应元hB(xi)中的数值个数都为1，在hA(xi)中其数值个数不都为1时，其犹豫度部分的相关系数定义如下：

其中lAi代表hA(xi)中数值的个数，lBi代表hB(xi)中数值的个数。

定理1[2]设A、B、C是非空集合X={x1,x2,…,xn}上的3 个犹豫模糊集，ρ(A,B)为A和B之间的相关系数，则ρ(A,B)满足以下3个性质：1）0 ≤ρ(A,B) ≤1；2）ρ(A,B) =ρ(B,A)；3）ρ(A,B) = 1, 如果A=B。

证明 改进的犹豫模糊集相关系数计算公式显然满足定理1 中性质的后两条，根据柯西-施瓦茨不等式，性质（1）证明如下：

由于给予两个部分偏好程度之和为1，所以综合可得

2.2 数值算例

应用文献[2]中的数值算例，为了更好地评估不同类型的软件Ai(i= 1, 2,…, 7)，根据功能性(x1)、可用性(x2)、可移植性(x3)、成熟度(x4)这4 个属性对软件进行聚类。分别对4 个属性赋予不同的权重ω={0.35,0.3,0.15,0.2}T，考虑到不同的评价专家具有不同的水平、背景、经验，会导致评估信息具有差异，为了准确反映专家意见，其评估信息用犹豫模糊集的形式表示在表1中。针对不同的偏好情况，将改进的新型相关系数计算公式（1）应用于HFSC算法[2]，得到的聚类结果如表2所示。

表1 文献[2]算例的决策矩阵Table 1 The decision matrix of the example in reference [2]

表2 文献[2]算例的各偏好对应聚类情况Table 2 The clustering of each preference of the example in reference [2]

通过对比可以发现，在使用本文改进的相关系数公式进行聚类时，当赋予犹豫模糊集隶属度差异部分和犹豫度差异部分的权重比大于等于1时，聚类效果与文献[2]的聚类效果相近，当赋予两部分的权重比小于1时，聚类效果差异较大。造成差异的原因一方面在于计算相关系数时，文献[2]中的相关系数公式需要人为主观填充数据，而改进的相关系数公式则避免了这一过程，保证了数据的真实准确性；另一方面，文献[2]中的相关系数只考虑一个影响相关系数的特征，如果只强调犹豫模糊元中数据的个体影响，其在一定程度上是正确的，当既考虑数据个体影响又考虑总体影响时，本文的聚类方法已涵盖了文献[2]中的情况，因此本文所提出的相关系数公式更为全面。

3 改进的区间值犹豫模糊集相关系数及算例分析

3.1 改进的区间值犹豫模糊集相关系数

定义8 将改进的犹豫模糊集相关系数的计算公式推广到区间值犹豫模糊集上，定义区间值犹豫模糊集相关系数计算公式为

其中，

α,β≥0且α+β= 1。ρWIVHFSX1(A,B)和ρWIVHFSX2(A,B)分别代表区间值犹豫模糊集隶属度部分的相关性。

对于区间部分的减法，采用左右端点部分等偏好的方法，具体形式如下：

根据改进相关系数公式的定义，为了保证其普适性，需要考虑分母为0的特殊情况.即2个区间值犹豫模糊集中各属性对应元中的区间个数都为1或其中一个为1这两种情况。当属性对应的区间值犹豫模糊元中区间个数都为1时，则规定在犹豫度部分其相关性为1；当各个属性对应元中的区间个数都为1，在中其数值个数不都为1时，其犹豫度部分的相关系数定义如下：

其中lAi代表中区间的个数，lBi代表中区间的个数。

证明 改进的区间值犹豫模糊集相关系数计算公式显然满足定理1中性质的后两条，性质（1）证明如下：根据柯西施瓦茨不等式可以得到：

对0 ≤ρWIVHFSX2(A,B) ≤1的证明与对0 ≤ρWHFSX2(A,B) ≤1的证明类似，综合可得0 ≤ρWIVHFSX(A,B) ≤1。

3.2 数值算例

一个汽车市场想要将6 辆不同的汽车Ai(i= 1, 2,…, 6)进行分类, 以下面4 个属性为衡量指标：安全性(x1)、燃油经济性（x2）、设计（x3）、价格（x4），分别对4 个属性赋予不同的权重，权重向量为ω={0.35,0.2,0.2,0.25}T，每辆车的评估数据用区间数的形式表达，如表3所示，表中数据代表专家对各个备选方案中各属性的满意程度，因此记为[0，1]内的区间值数字。

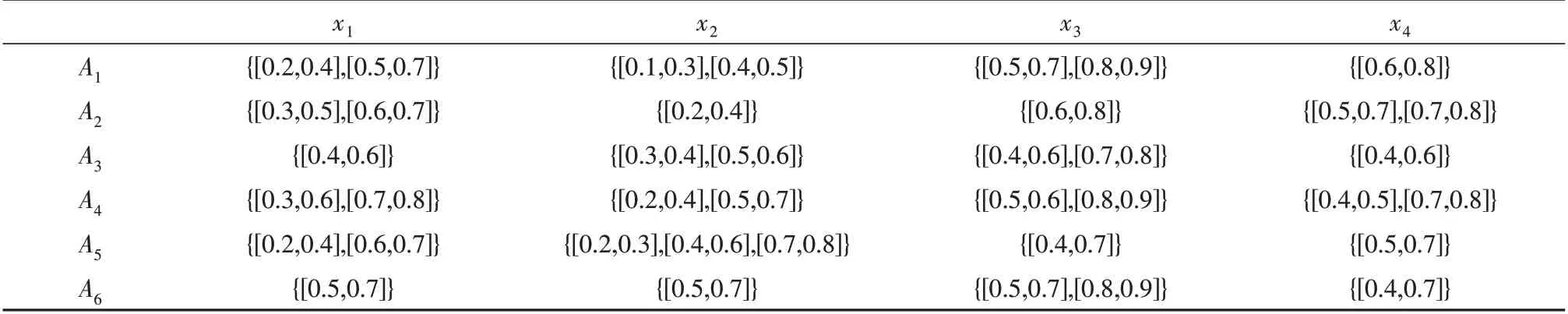
表3 本文算例的决策矩阵Table 3 The decision matrix of the example in this paper

针对不同的偏好情况，将改进的新型相关系数计算公式（2）应用于HFSC算法[2]，得到的聚类结果如表4所示。

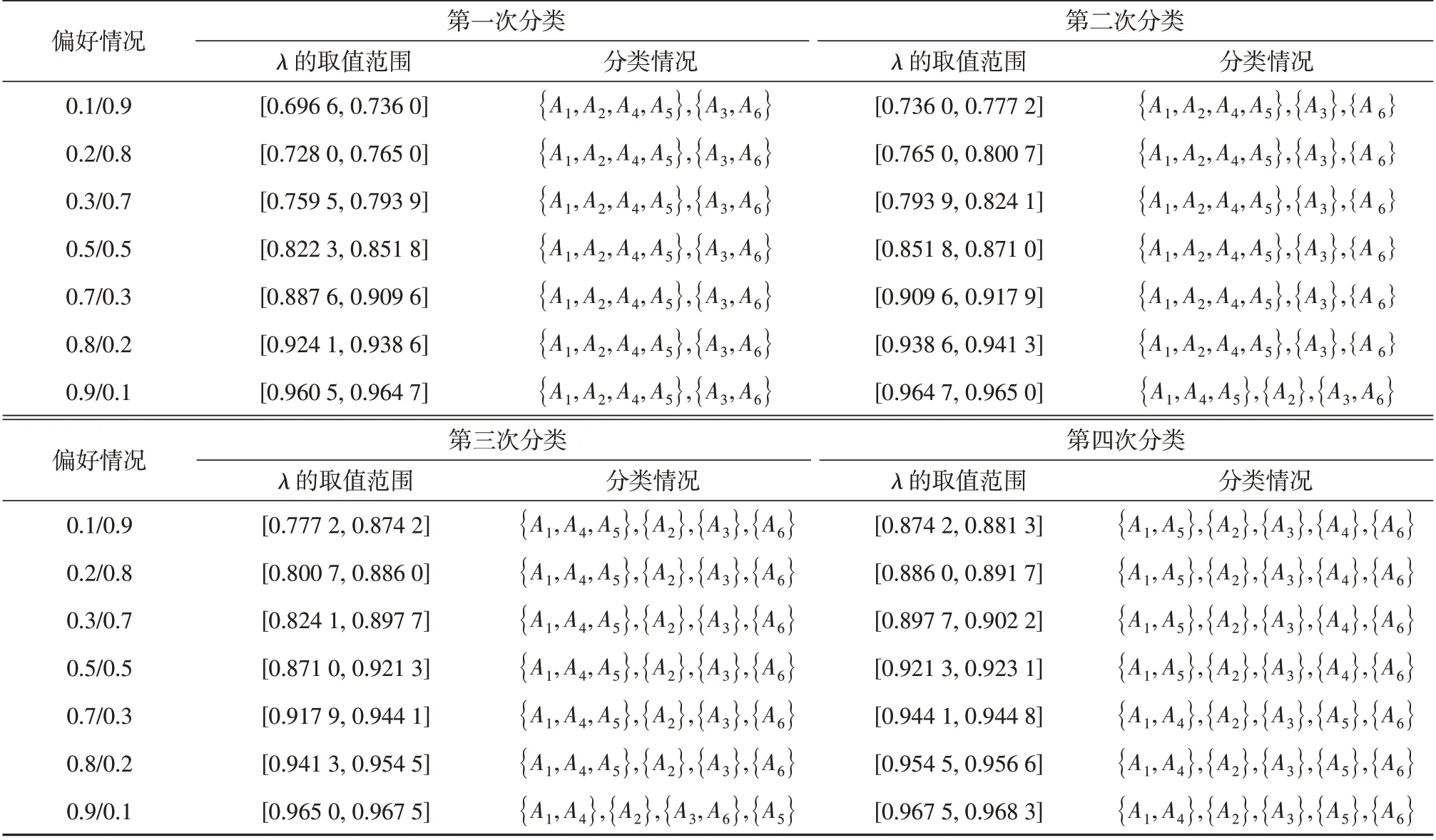
表4 本文算例的各偏好对应聚类情况Table 4 The clustering of each preference of the example in this paper

将得到的犹豫模糊集之间的相关系数计算公式推广到区间上，通过数值计算可以得到，在区间值犹豫模糊集中当赋予ρWIVHFSX1和ρWIVHFSX22个部分不同的偏好时得到的聚类情况也有所不同。对比已有研究中只考虑了对应区间值犹豫模糊元之间的隶属度值对总体相关性带来的影响，本文还将对应区间值犹豫模糊元的内部差异作为衡量相关性的指标，考虑了2个影响相关系数的特征，比传统相关系数只考虑单一特征更为全面。

4 结论

改进的相关系数计算公式弥补了现有公式中需要进行主观填充的不足，另外，将犹豫度作为衡量相关性的另一指标加入公式中，把内部偏差考虑在内，用于衡量内部总体差异。无论是犹豫模糊集还是区间值犹豫模糊集，通过数值计算可以发现，当赋予隶属度差异部分和犹豫度差异部分不同的权重偏好时得到的聚类结果不同。本文的聚类方法已涵盖了只考虑单一特征的情况，另外，通过理论证明了新公式的科学性，因此本文改进的相关系数公式是合理有效的。