关于指数丢番图方程((mk1+m1)n-1)((mk2+m2)n-1)=x2的求解

罗永亮,杨 海,陈江涛

(西安工程大学理学院,陕西 西安 710048)

1 引言及结论

设Z,N*分别表示全体整数和正整数的集合,且a,b是大于1的正整数,近些年来,讨论方程

(an-1)(bn-1)=x2,x,n∈N*,

(1)

的正整数解问题成为数论中的一个引人注目的重要课题.对此,COHN J H E[1]证明了:当(a,b)=(2,3),(2,6)时,方程(1)无解.同时,HAJDUL[2],SZALAY L[3]还对b=ak,对于其中k是大于1的正整数情况,给出了方程(1)正整数解的相关结论.另外,贺光荣[4]还讨论了更一般的方程

(an-1)(bn-1)=x2,x,m,n∈N*,

(2)

证明了当(a,b)=(2,3)时,方程(2)无正整数解.近些年来诸多学者如梁明[5],付瑞琴[6],杨海[7]和Refik Kidskin[8]研究此类及相关的指数丢番图方程,得出了许多很有价值的结论,积极推动这一类型方程的解决.此外,潘承洞,潘承彪[9]在初等数论一书中严谨系统地给出了初等数论的基本方法和经典结论,为解决丢番图方程问题提供了理论基础.

唐波,杨仕春[10]研究了方程((10k1+2)n-1)((10k2+3)n-1)=x2,k1,k2∈N*的正整数解,并给出方程无正整数解时的情况.

乐茂华[11],曹珍富[12],华罗庚[13]等分别介绍了在不同条件下指数丢番图方程的正整数解的问题,并给出了研究此类问题的一些方法和结论.

杨仕椿,吴文权[14]给出了方程((13k1+5)n-1)((13k2+8)n-1)=x2,k1,k2∈N*与((17k1+6)n-1)((17k2+7)n-1)=x2,k1,k2∈N*解的一些相关的结论.

乐茂华[15]证明了方程(2n-1)((6k)n-1)=x2,k,n,x∈N*没有正整数解(n,x).

由于方程(1)在研究某类特定的指数方程以及在代数学中的群论以及密码学等领域中有较为深刻的应用,因此研究a,b取较大正整数时,方程(1)的解的情况是非常有必要的.

本文将研究指数丢番图方程

((mk1+m1)n-1)((mk2+m2)n-1)=x2,x,n∈N*,

(3)

其中

m,m1,m2,p,k1,k2,x,n∈N*;以及方程

((mk1+m1)n-1)((mk2+m2)n-1)=x2,x,n∈N*,

(4)

其中

m,m1,m2,p,k1,k2,x,n∈N*.在研究过程中,主要运用二次剩余的初等方法和已被证明的经典结论,给出了关于这两个方程在特定条件下解的情况.

定理1.1 设m1+m2≡0(modm),当n≡0,1,3(mod4)时,方程(3)和(4)均没有正整数解(n,x).

定理1.2 设m1+m2=(8q-7)m,q∈N*,当

(i)k1≡0,2(mod8),k2≡0(mod2);

(ii)k1≡1(mod2),k2≡5,7(mod8);

以上两个条件任意一个成立时,则方程(3)没有正整数解(n,x).

定理1.3 设m1+m2=(8q-7)m,q∈N*,当

(i)k1≡4,6(mod8),k2≡0(mod2);

(ii)k1≡1(mod2),k2≡5,7(mod8);

以上两个条件任意一个成立时,则方程(4)没有正整数解(n,x).

符号说明:对任意的素数p,pa‖n表示pa恰好整除n,而pa+1不整除n;读作pa恰整除n.

2 引理

引理2.1[13]若4|n,则方程(1)仅在(a,b)=(13,239)时有解,而且仅有解(n,x)=(4,9 653 280).

引理2.3 若k,A均为奇数,则方程2kA=x2没有正整数解.

证明:由k,A均为奇数,则2kA质因数分解中的2的次幂为奇数k,因为x2质因数分解中的2的次幂必为偶数,所以方程2kA=x2没有正整数解.

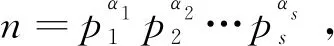
引理2.5[9]设p为质数,Legendre符号具有以下性质:

引理2.6[9]设p为质数,Jacobi符号具有以下性质:

引理2.7[9]设P>1的奇数,则有

3 定理证明

定理1.1的证明

根据引理1.1,假设方程(3)和(4)在n=0(mod 4)时,存在(a,b)=(13,239),则

a+b=239+13=22×32×7≡0(modm),

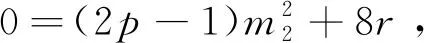
当m=21时,可得21k1+m1=13或21k2+m2=13,因为k1,k2,m1,m2均为正整数,等式不成立.

故方程(3)和(4)在n=0(mod 4)条件下,没有正整数解(n,x).

因为

定理1.2的证明

S=((mk1+m1)n-1)((mk2+m2)n-1)=

((mk1+m1)2-1)((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1).

令A=((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1),则A为奇数.

当k1≡0(mod 8)时,设k1=8t,则

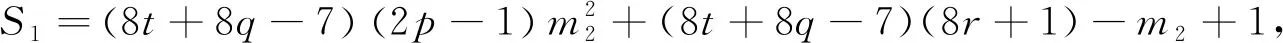
由m2≡2(mod 8),得4‖S1,2‖S2,进而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(3)无正整数解(n,x).

当k1≡2(mod 8)时,设k1=8t+2,则

由m2≡2(mod 8),得4‖S2,2‖S1,进而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(3)无正整数解(n,x).综上以上两种情况,即得方程(3)满足条件(i)时,无正整数解(n,x).

S=((mk1+m1)n-1)((mk2+m2)n-1)

=((mk2+m2)2-1)((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1).

设A=((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1),则A为奇数.

当k2≡5(mod 8),设k2=8t+5,则

由m2≡2(mod 8),得4‖S1,2‖S2,进而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(3)无正整数解(n,x).

当k2≡7(mod 8),设k2=8t+7,则

因为m2≡2(mod 8),得2‖S1,4‖S2,进而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(3)无正整数(n,x).综合以上两种情况,即得方程(3)满足条件(ii)时,无正整数解(n,x).故方程(3)满足条件(ⅰ) (ⅱ) 任意一种情况时,无正整数解(n,x).定理1.2证毕.

定理1.3的证明

S=((mk1+m1)n-1)((mk2+m2)n-1)=

((mk1+m1)2-1)((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1).

令A=((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1),则A为奇数.

当k1≡4(mod 8)时,设k1=8t+4,则

由m2≡6(mod 8),得4‖S1,2‖S2,进而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(4)无正整数解(n,x).综上以上两种情况,即得方程(4)满足条件(i)时,无正整数解(n,x).

当k1≡6(mod 8)时,设k1=8t+6,则

由m2≡6(mod 8),得2‖S1,4‖S2,进而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(4)无正整数解(n,x).综上以上两种情况,即得方程(4)满足条件(i)时,无正整数解(n,x).

S=((mk1+m1)n-1)((mk2+m2)n-1) =

((mk2+m2)2-1)((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1).

令A=((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1),则A为奇数.

当k2≡1(mod 8),设k2=8t+1,则

由m2≡6(mod 8),得4‖S1,2‖S2,进而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(4)无正整数解(n,x).综合以上两种情况,即得方程(4)满足条件(ii)时,无正整数解(n,x).

当k2≡3(mod 8),设k2=8t+3,则

由m2≡6(mod 8),得2‖S1,4‖S2,进而可得8‖(mk2+m2)2-1,故23‖S,由引理3可知方程(4)无正整数解(n,x).综合以上两种情况,即得方程(4)满足条件(ii)时,无正整数解(n,x).

故方程(4)满足条件(ⅰ) (ⅱ)任意一种情况时,无正整数解(n,x).定理1.3证毕.

4 结论

关于方程(an-1)(bn-1)=x2,x,n∈N*可解性的探究还远未完成,众多学者在限定a,b参数情况下,讨论了这一类型方程的正整数解,得到了很多具有价值的结果;显然根据文中三个定理,可以探究出无穷多组该方程无正整数的情况,为推动解决此类丢番图方程的问题提供一定思路和方法.