异质Erdös-Rényi随机超网络上的演化博弈
王浩羽,刘兴文,吴 琼
(西南民族大学电气工程学院,四川 成都 610200)
囚徒困境博弈模型和雪堆博弈模型[1]作为两人两策略对称博弈模型得到广泛研究.在这些博弈中,个体可以选择合作或背叛,而使个体利益最大化的策略通常是背叛.达尔文理论指出,利他行为(合作)最终会在生存斗争中消失[2].众所周知,群体合作在演化博弈中至关重要[3].为了提高合作水平,Hamilton等人提出,如果个体离出生地不远,那么集群是有粘性的[4].一般认为这种有限的分散可以通过增加个体间的相互作用而促进合作水平.此外,早期研究表明,空间结构可能仍然不利于雪堆博弈中个体间的合作[5].但最近研究发现,在多重交互动力学的条件下,当成本效益比在较大范围内,空间结构仍有利于雪堆博弈中合作行为的出现[6].
如今的社交网络呈现出各种各样的多样性[7-8],社交群体和个体之间的关系更加复杂[9].复杂网络已经被用来描述和分析现实世界中复杂的物体,并在不同的科学领域得到了广泛的应用[10].许多学者一直在研究各种网络上的演化博弈规律[11].如,Du等人建立了一个纳什博弈模型来衡量两阶段结构网络中决策个体的收益[12].
在某些情况下,使用简单图表示复杂网络是不能完全描述真实世界的场景.以一所中学的教师群体为例.这些教师之间可能存在多种不同的关系(例如,互相认识的教师群体,教授同一个班级的教师群体,教授同一类别课程的教师群体),很难用简单图来描述这些关系.Esreada等人提出了用超图表示这些关系的超网络,使对复杂系统进行拓扑分析成为可能[13].在简单图中,一条链接只与一对节点相关.但在超图中,一条边(称为超边)是与一个群(组)相关.换句话说,超边不仅可以表现节点与节点之间的关系,还可以表现节点群之间的关系[14-15].
Erdös和Rényi提出的随机网络模型是复杂网络中常用的网络模型之一[16].ER随机网络已被广泛研究和应用于不同领域[17-18].Lu[19]等人基于ER随机网络理论构造了一个可能包含孤立点的ER随机超网络模型.对于社会群体来说,孤立个体的存在是无益的[20].此外,如果一个个体是孤立的,它就没有邻居与之博弈.囚徒困境博弈和雪堆博弈是两人对称博弈,故研究博弈中的孤立个体是没有意义的.
文献[19]中的ER随机超网络是同质的(homogeneous),并不能真实地描述现实世界的异质性.在此基础上,本文首先改进了文献[19]中的同质ER随机超网络,然后研究了该网络上的演化囚徒困境博弈和演化雪堆博弈.主要贡献如下:
1)提出一种避免孤立点的异质(heterogeneous)ER随机超网络模型;
2)研究基于无条件模仿规则,赢留输换策略更新规则和断连机制的演化博弈.
1 模型
首先回顾囚徒困境博弈(PDG)和雪堆博弈(SDG).两种博弈都是两策略两人对称博弈,两种策略分别是合作(C)和背叛(D).双方个体在相互合作时获得收益R,在相互背叛时获得收益P;如果一个个体合作,而另一个背叛,那么合作者将获得收益S,背叛者将获得收益T.个体的收益矩阵可表示如下[5]:

(1)
故,PDG的收益矩阵如下:

(2)
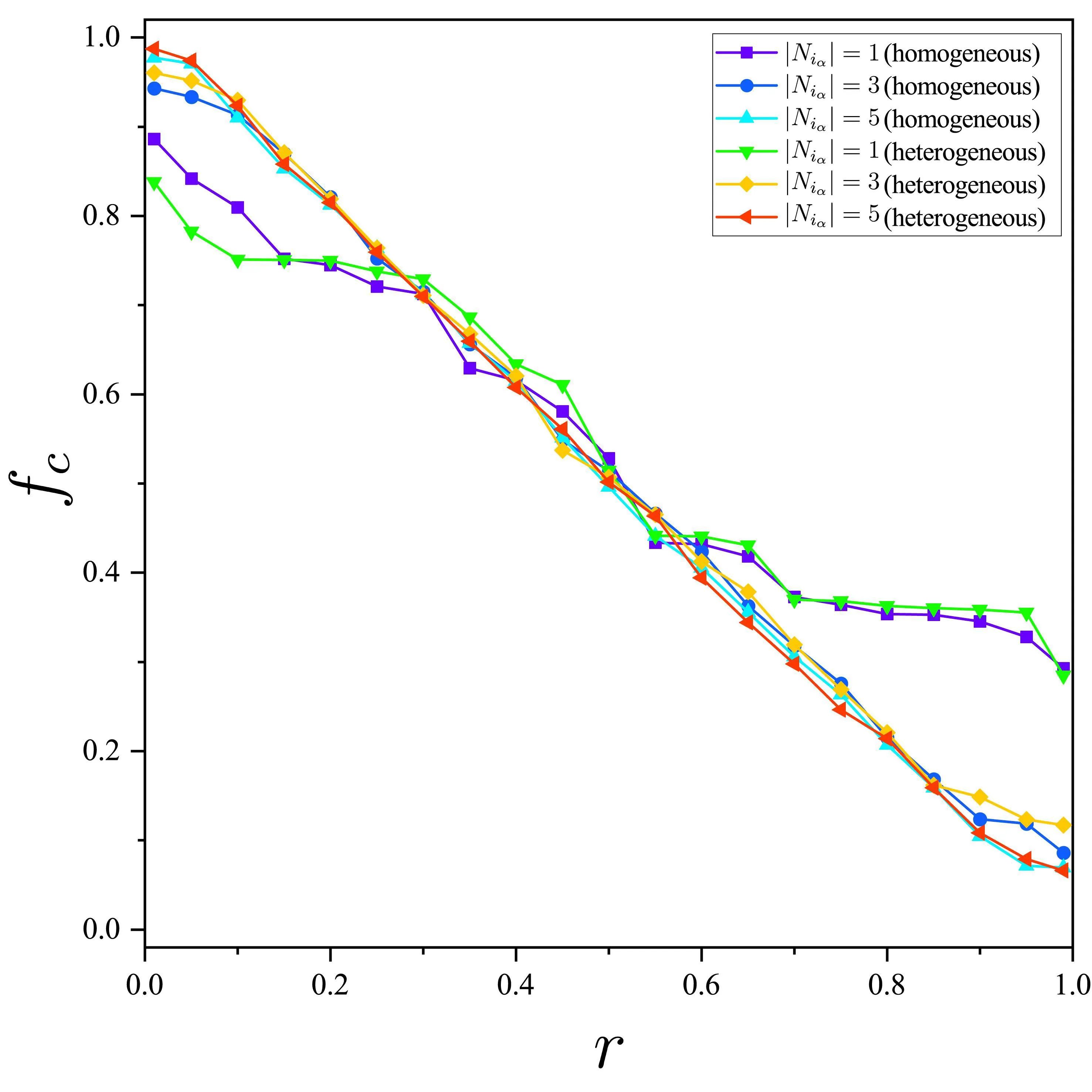
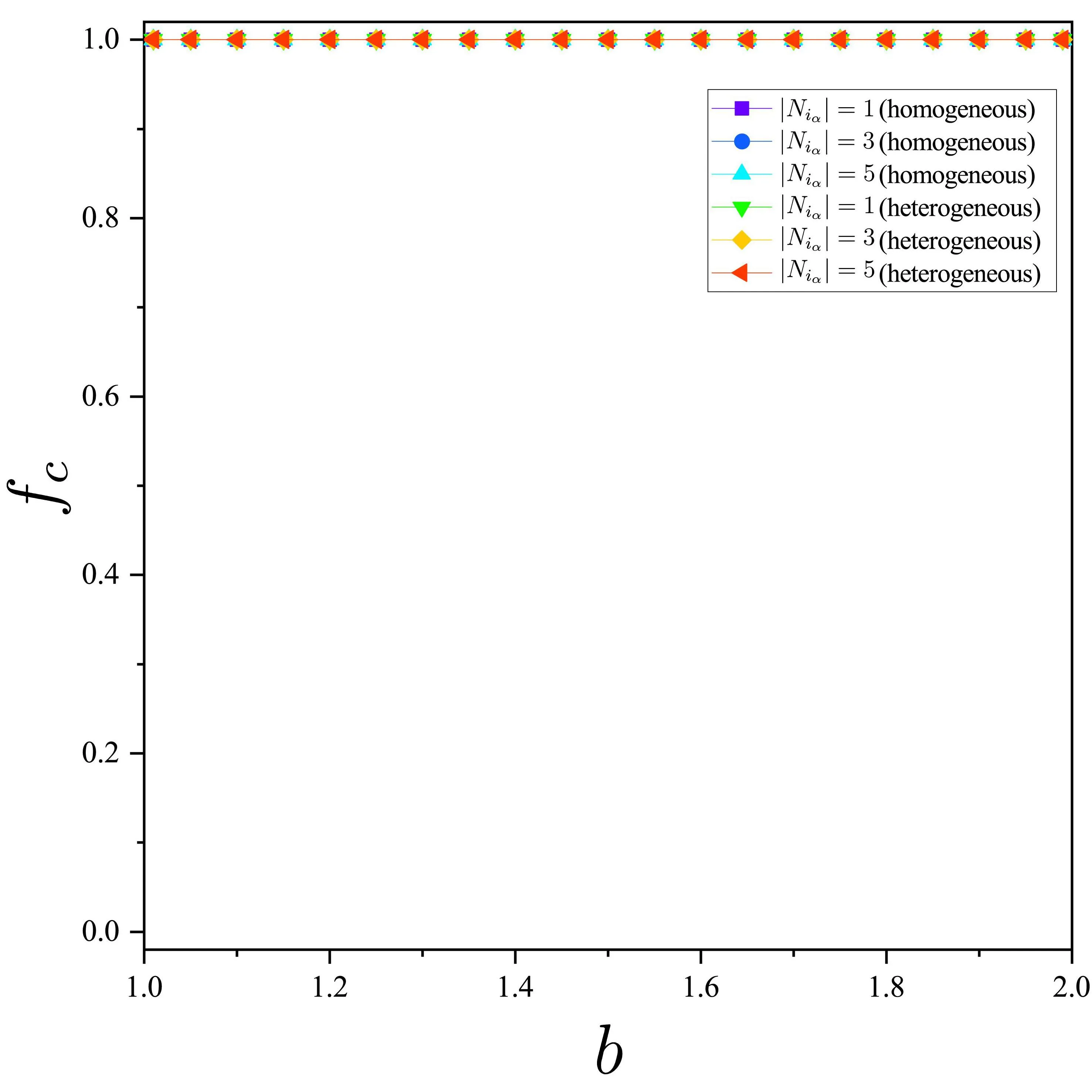
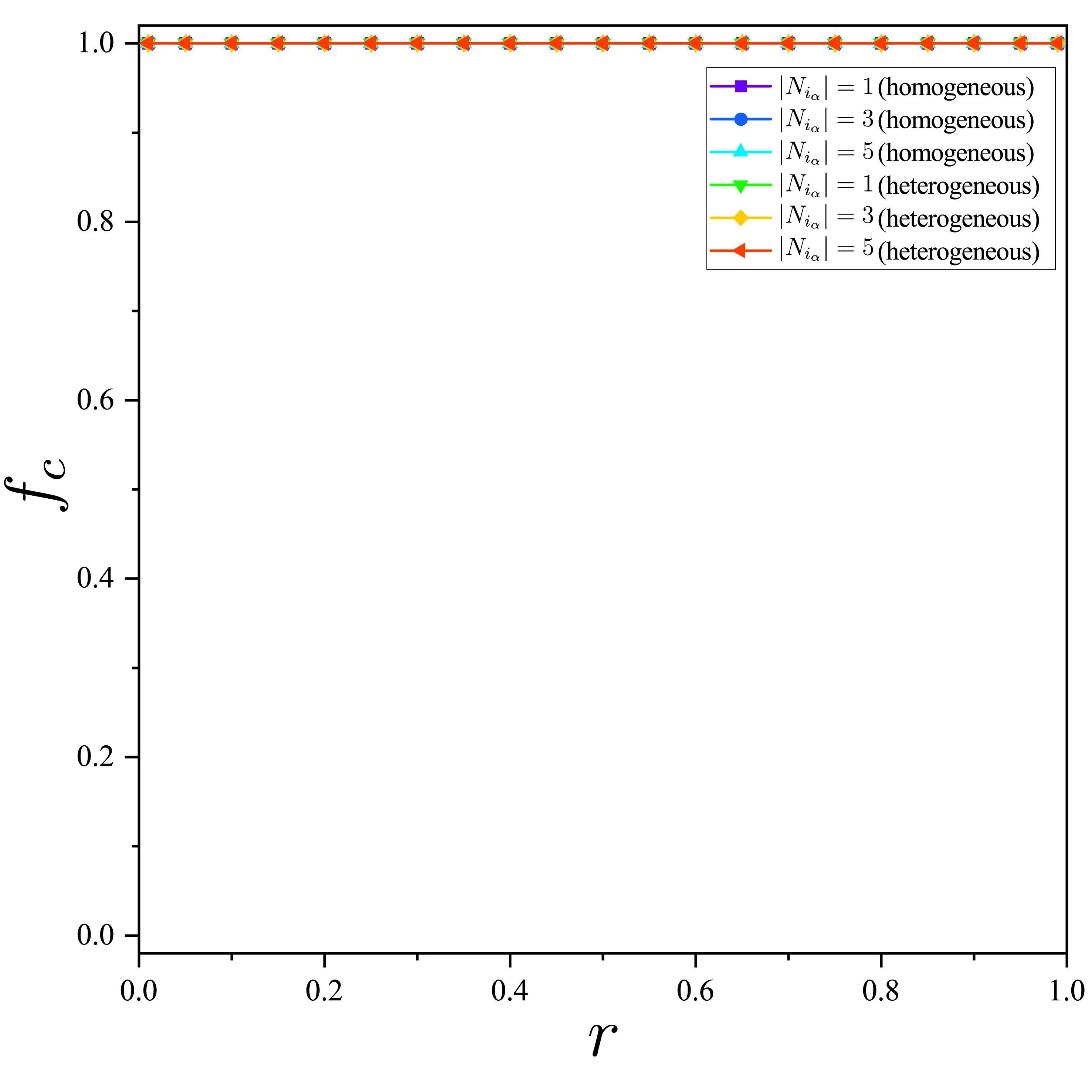
其中,b代表诱惑因子,且1 (3) 其中,r是成本效益比,且1 在文献[19]中描述的ER随机超网络是同质的,且有两个缺点:每条超边都包含相同数量的节点,这往往不能描述现实世界中的真实情况;此外,该网络仍然可能存在孤立节点.当今社会,孤立节点的存在不利于个体间的合作. 为了克服这两个缺点,本文提出了一种异质ER随机超网络,构建步骤如下: ③如果这l个节点已经属于同一条超边,则返回步骤②; ④生成一个随机数pr∈[0,1].如果pr ⑤重复步骤②至步骤④,直到任意一个节点都至少属于一条超边. (a) (b) 图1(a)为同质ER随机超网络的一个示例,其中n=30,每条超边的度为5.图1(b)为异质ER随机超网络的一个示例.假设一条超边中的所有节点彼此互为邻居(例如,在图1(a),1(b)中,v1是v2的邻居,则v2也是v1的邻居),反之亦然.也就是说,如果部分节点之间互为邻居,那么它们必然属于同一条超边. 在图1(a)中,节点v1只属于E1,其邻居集如下: 而节点v11属于超边E3,E4和E9,因此它的超度为3,它的邻居集为 考虑演化博弈是基于ER随机超网络上的.观察图1,我们可以看到,当网络中的个体数量足够大,一个个体将有很多邻居.可以合理地假设vi在每一轮中只与它的邻居集的一个子集博弈.为了说明清楚,给出以下定义. 潜在邻居:集合Ni中的所有个体.设|Ni|是vi的潜在邻居数.注意,在晶格网络上的演化博弈,每个个体通常有4或8个潜在邻居[21]. 1)Niα(t)是vi的交互邻居集,其中的每个个体由vi选择博弈; 2)Niβ(t)是vi的交互邻居集,其中的每个个体选择vi博弈. 一次独立的演化博弈过程如下: 1)初始化:以50%的概率给每个个体随机分配一个策略(C或D); 2)在第t(t>1)轮博弈中,个体vi从Ni中随机选择|Niα|个潜在邻居构成Niα(t).在仿真中,为了使博弈相对公平,|Niα|为一个固定的值.但在每一轮的Niα(t)都不是固定的. 当所有个体确定自己的Niα(t),则Ni(t)也确定.当所有个体完成博弈.个体vi的累计收益Pi(t)计算如下: 其中,Pi,j(t)是当vi完成第t轮与vj的博弈的收益,由收益矩阵(1)决定.所有个体在博弈中使用收益矩阵(1)来计算收益. 3)在完成第t轮博弈后,每个个体都使用策略更新规则来更新第(t+1)轮博弈的策略. 本文采用两种策略更新规则,具体如下: R1.无条件模仿更新规则[22](The unconditional imitation rule):假设第(t-1)(t≥2)轮博弈已经结束.vi随机选择一个潜在邻居vj.如果Pi(t-1) R2.输换赢留策略更新规则[21](The WSLS rule):当t>2时,vi随机选择一个潜在邻居vj,并以概率pi(t)使si(t)=sj(t-1),其中pi(t)由费米函数计算求得;否则,使si(t)=si(t-1).费米函数如下: 4)重复步骤2)-3),直到合作水平达到相对稳定. 以往断连机制(The disconnection mechanism)常被采用于晶格网络[23]上的演化博弈.接下来,为了适应ER随机超网络上演化博弈,断连机制的步骤如下: 步骤5:结束. 在确定所有个体与互动邻居都完成了第t轮博弈后,每个个体采用WSLS规则更新自己第(t+1)轮博弈的策略. 接下来,我们将根据策略更新规则和博弈机制,分析仿真并得出主要结论.首先提供晶格网络上的PDG和SDG的合作水平图,如下: (a)基于晶格网络的囚徒困境的合作水平 (b)基于晶格网络的雪堆博弈的合作水平图2 采用不同策略更新规则的囚徒困境博弈和雪堆博弈的合作水平图Fig. 2 Cooperation levels of PDG and SDG with different strategy updating rules 首先讨论PDG.观察图2(a)中晶格网络上的PDG.当个体采用无条件模仿规则,每个个体的目标是在下一次博弈中获得相对较高的收益.由蓝色的三角线可知,对于任一满足条件1 (a)基于同质ER随机超网络上的演化PDG (b)基于同质ER随机超网络上的演化SDG (c)基于异质ER随机超网络上的演化PDG (d)基于异质ER随机超网络上的演化SDG (e)b=1.5时的合作频率 (f)r=0.5时的合作频率 图3(a)和图3(c)展示了同质ER随机超网络和异质ER随机超网络上的演化PDG的结果.对于任意b满足1 现在讨论雪堆博弈.图2(b)清楚地表明,晶格网络上的SDG中的r存在阈值.当r∈(0,0.25]时,fc=1;当r∈[0.77,1)时,fc=0.当0.25 在同质ER随机超网络和异质ER随机超网络上的雪堆博弈,r对fc的影响类似于图3(b)和图3(d).与图2(b)晶格网络上的结果相比,fc在ER随机超网络上的曲线“更线性”,即随着r的增加,fc逐渐降低,两种ER随机超网络始终处于合作者和背叛者共存的状态.与晶格上的结果不同的是:无论r的值是多少,异质ER随机超网络上的fc都不会达到1和0.图3(b)和3(d)表明,当T较小时,大量的个体是合作者.实际上,当r趋于0时,大量的个体自发成为合作者,而当r趋于1时,网络也不会形成一个完全的背叛者集群. 通过对比图3(b)和图3(d),可以得出以下结论: 1)在区间(0,1)的第一部分,固定|Niα|,r越小,fc越大; 2)在区间(0,1)的中间部分,固定|Niα|,fc几乎呈线性衰减; 3)在区间(0,1)的最后一部分,固定|Niα|,r越大,fc越小; 4)在区间(0,1)的第一部分,固定r的值,|Niα|越大,fc越大; 5)在区间(0,1)的中间部分,固定r的值,|Niα|越大,fc越小. 上面的结论对同质ER随机超网络和异质ER随机超网络都成立. 从图3(b)和图3(d)可以看出,对于相同的|Niα|,SDG的fc曲线在同质ER随机超网络和异质ER随机超网络上的差异非常小. 图3(f)揭示了一个有趣的现象:异质ER随机超网络上的fc(t)曲线总是在演化博弈的第2轮显著下降,然后增长到约50%.而在同质ER随机超网络上不存在类似的现象. 在采用WSLS规则时,在公式(5)中,给定参数κ=0.01.晶格网络和ER随机超网络的结果分别如图2和图4所示. 如上一小节所述,我们首先讨论PDG,然后再讨论SDG. 观察图2(a)和图4(a).无论是晶格网络,同质ER随机超网络和异质ER随机超网络中的哪一种,PDG的fc(t)曲线均趋于零.图4(c)显示当b=1.5时,fc(t)从50%下降到0.当时间步长小于100时,异质ER随机超网络上的fc(t)的下降速度比同质ER随机超网络上的fc(t)快.注意,κ=0.01意味着所有的个体都是相对理性的,因此当一个策略给了个体带来了比它的邻居更低的累计收益,该个体就会倾向于更新自己的策略以获得更高的累计收益.在(2)中,收益T大于P,R等于S,所有个体为了追求高收益都成为了背叛者. 由图4(b)中两种ER随机超网络上的SDG的fc曲线可得:随着SDG中r的增加,fc逐渐减小.与图2(b)中晶格网络上的结果相似的是,ER随机超网络上的fc曲线表现出了网络中存在从有大量合作者的混合状态到有大量背叛者的混合状态的变化;不同的是,fc在ER随机超网络上的曲线更线性,不存在完全合作或完全背叛的状态.从图4(d)可以看出,当r=0.5时,fc(t)稳定在50%左右.有趣的是,基于异质ER随机超网络上的SDG的fc(t)曲线在第二轮急剧下降. 当采用断连机制,我们给定参数pd=0.5.在晶格网络和ER随机超网络上的结果分别如图2和图5所示. 观察图2和图5.基于晶格网络,同质ER随机超网络和异质ER随机超网络上的PDG和SDG的fc(t)曲线均趋向于1.可以得到,断连机制对fc有显著的促进作用.对比图5(c)和图5(d)中同质ER随机超网络的演化曲线,异质ER随机超网络在第二轮出现大量的背叛者,导致fc(t)急剧下降,随后fc(t)迅速上升,最后达到1. (a)演化PDG的合作水平 (b)演化SDG的合作水平 (c)b=1.5时的合作频率 (d)r=0.5时的合作频率图4 采用WSLS规则的囚徒困境和雪堆博弈的合作水平图和合作频率图Fig. 4 Cooperation level and cooperation frequency of PDG and SDG with the WSLS rule (a)演化PDG的合作水平 (b)演化SDG的合作水平 (c)b=1.5时的合作频率 (d)r=0.5时的合作频率图5 采用断连机制的囚徒困境和雪堆博弈的合作水平图和合作频率图Fig. 5 Cooperation level and cooperation frequency of PDG and SDG with the disconnection mechanism 图5(c),5(d)表明|Niα|对fc(t)的有以下影响: 1) 在同质ER随机超网络和异质ER随机超网络中,|Niα|越大,fc(t)演化趋于稳定的速率越快; 2) 在异质ER随机超网络中,|Niα|越小,在第二轮中选择背叛的个体越多. 从图5(c)和图5(d)可以看出,在断连机制中,无论是在同质ER随机超网络还是异质ER随机超网络中,|Niα|对PDG和SDG的fc(t)趋于1的结果是没有影响的. 我们首先提出了一种异质ER随机超网络.与同质ER随机超网络相比,新网络有两个主要优点:可描述多层结构和排除孤立点.此外,研究了同质和异质ER随机超网络上的演化博弈 (PDG和SDG).研究发现:异质ER随机超网络的合作水平具有与同质ER随机超网络相似的演化结果;异质ER随机超网络上的合作水平曲线比晶格网络上的合作水平曲线更“线性”;异质ER随机超网络中的参数|Niα|对合作水平是有影响的.我们未来的研究重点是异质ER随机超网络中的其他参数对合作水平的影响.

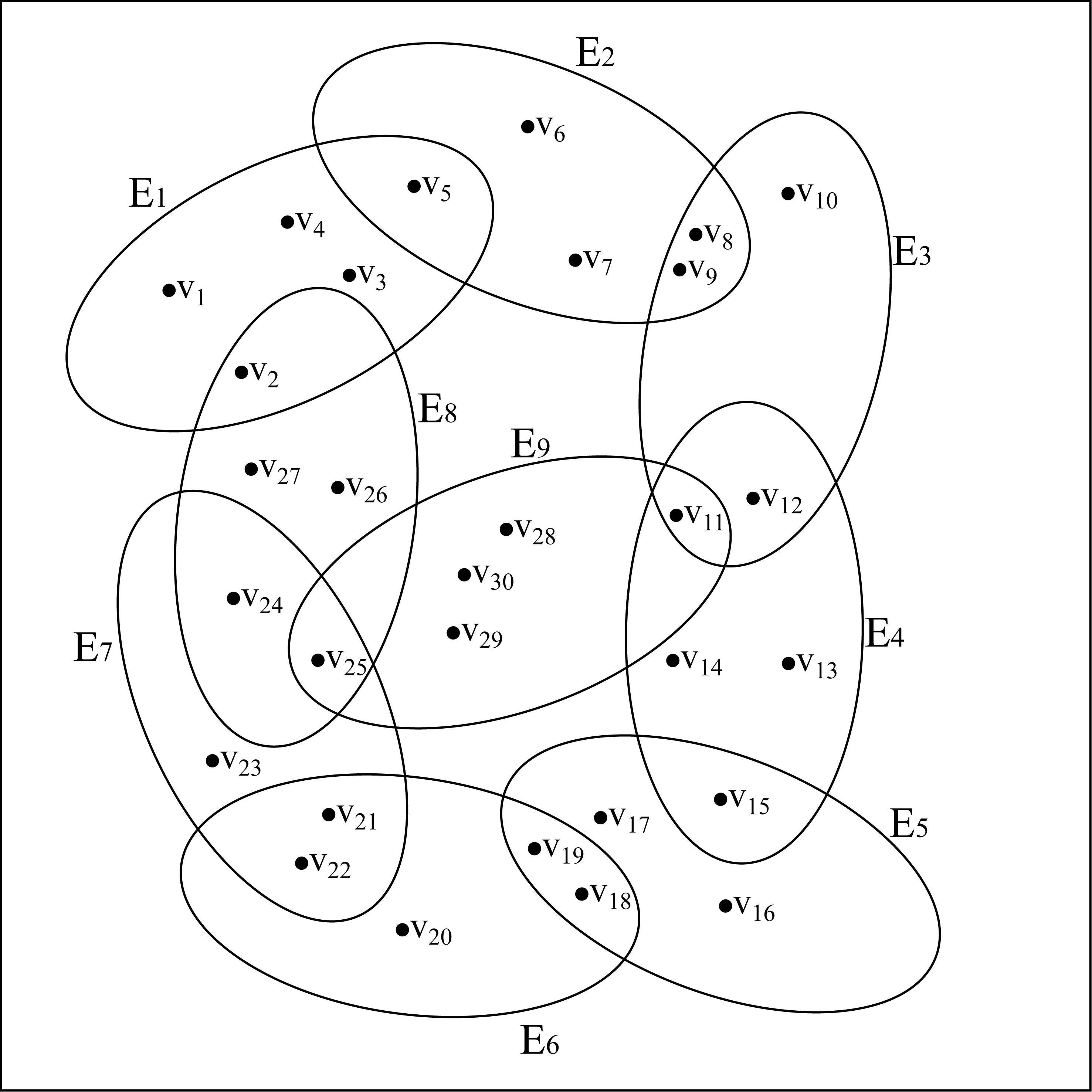

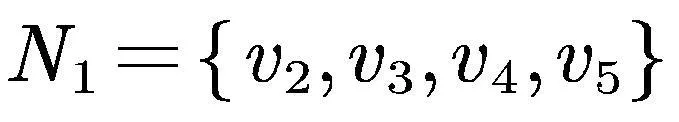
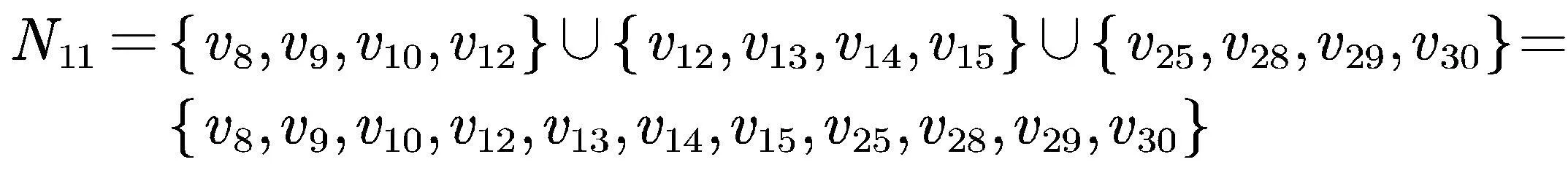





2 实验和结果







2.1 采用无条件模仿规则下的合作水平






2.2 采用输换赢留规则下的合作水平

2.3 采用断连机制下的合作水平

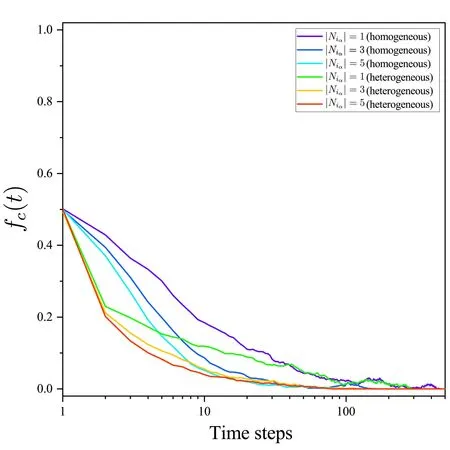




3 结论

