基于GPU和Python的粒子群优化算法研究
熊大卫,胡 建,陈 园
(西南民族大学计算机科学与工程学院,四川 成都 610041)
群体智能算法已被应用于众多领域,例如数据分析[1]、半结构化数据查询优化[2]、图像分割[3]等.但是,由于群体中的个体间相互作用、包含多个随机操作符等原因,导致群体智能算法具有复杂的随机性和动态性,计算时间较长.因为个体间存在内在并行性,故可采用图形处理器(Graphics Processing Unit,GPU)通过并行计算的方式[4]加速群体智能算法.
粒子群优化算法(Particle Swarm Optimization,PSO)是群体智能算法中最具代表性的一种,目前主要应用于如下几个领域:神经网络训练,如文献[5]利用PSO算法调整深度信念网络的内部参数,提出了一套输电线路电晕损耗预测方法,文献[6]基于PSO算法提出优化BP神经网络的PID控制算法;函数优化,如文献[7]提出多策略混合进化的PSO算法求解大规模函数优化问题,文献[8]提出一种利用种群进化的改进PSO算法求解多模态函数优化问题;路径规划,文献[9]提出利用差分进化算法改进的PSO算法,求解动态窗口法的动态路径规划问题,文献[10]基于一种改进的PSO算法,求解多目标点路径规划问题.与其他群体智能算法一样,可采用GPU的CUDA架构(Compute Unified Device Architecture,CUDA)[11],通过并行计算的方式加速PSO,例如文献[12]以PSO算法为例,研究如何利用CUDA平台进一步发挥群体智能算法的并行性优势;文献[13]利用CUDA架构并行实现了柯西振荡粒子群优化算法(CO-PSO);文献[14]应用PSO算法优化克里金算法中的克里金参数,并通过CUDA架构加速PSO算法以提高插值效率.
近年人工智能飞速发展,作为深度学习领域首选编程语言的Python语言使用率也随之激增.照此趋势,Python相较于其他程序语言的绝对主流地位与PSO在高维复杂优化问题领域的卓越性能都预示这两者的结合趋于必然.但据我们调研,未见PSO算法基于Python语言实现GPU加速的报道.
对此,本文基于Python语言,以CUDA架构、Numba库[15]为工具提出了利用GPU加速的改进PSO算法,并经实验证明能达到有效的加速效率.这将为基于GPU和Python的PSO并行加速提供有价值的参考.
1 PSO算法简介
PSO算法称解空间中的点为粒子,所有粒子构成种群.各粒子具有初始速度和位置,并根据种群的经验来调整自己的运动,最终找到全局最优位置[16],其伪代码如下所示.

Algorithm PSO1: Initial Swarm in CPU //初始化种群2: For i←1 to Iterations:3: For j←1 to P:4: Evaluate Particle //粒子评价5: Check and Update Pbest //更新个体历史最优解6: Check and Update Gbest //更新全局最优解7: Forj←1 to P:8: UpdateVelocity and Position //粒子升级9: Return the bestPosition and Fitness
其中,Swarm表示种群,Iterations为迭代代数,P为种群大小,Particle表示粒子,Pbest和Gbest分别表示个体历史最优解和全局最优解,Velocity和Position分别表示速度和位置,按照公式(1)与公式(2)进行更新,Fitness为适应度值.
(1)
(2)
上述公式中,当前维数d=1,2……D,D表示最大维数;t为当前代数;第i个粒子的速度向量记为Vi=(Vi1,Vi2……Vid),位置向量记为Xi=(Xi1,Xi2……Xid),其中i=1,2……P;待优化问题边界根据测试函数设定记为[Xmin,Xmax]D,速度和位置更新后,若Xid>Xmax,则Xid=Xmax;若Xid 在不同版本PSO算法中参数取值各有不同,但参数值的选取并不会在很大程度上影响本文所关注的算法运行时间.本文为简便起见,参数设置如下:惯性因子w表示上一代粒子的速度对当代粒子速度的影响,使粒子保持运动的惯性和搜索扩展空间的趋势,较大的w有利于全局搜索、跳出局部最优解,而较小的w有利于局部搜索、让算法快速收敛到最优解,w的典型取值范围是[0,1.5],本文按照基本粒子群算法将w设置为0.5[17];认知因子c1表示粒子下一步动作来源于自身经验部分所占的权重,社会因子c2表示粒子下一步动作来源于其它粒子经验部分所占的权重,当c1和c2都不为0时算法更容易保持收敛速度和搜索效果的均衡,本文将c1和c2分别设置为1和2[18];随机数r1与r2为服从[0,1]上的均匀分布随机数,加入此项以提升算法搜索的随机性. Python作为一种解释性语言运行速度较慢,本文选择Numba库通过即时编译技术(Just In Time,JIT)[19]对程序进行加速. 相较于标准PSO算法,PSO-CUDA算法中种群初始化方式不变,将粒子评价、更新个体历史最优解、粒子升级三个部分改用GPU并行计算分别完成.由于全局最优解的更新过程中涉及大量的逻辑判断,虽然GPU有逻辑运算能力,但GPU不具备CPU的分支预测能力,只能顺序执行逻辑分支,且过程中可能因为Warp Divergence[20]产生不必要的时间开销,故将更新全局最优解的步骤置于CPU中完成. PSO-CUDA算法流程可概括如下:1)于CPU中完成种群及所需参数初始化;2)拷贝种群至GPU;3)于GPU中调用核函数完成粒子评价、更新个体历史最优解、粒子升级;4)拷贝种群至CPU;5)更新全局最优解.基于Python语言实现的CUDA版本改进PSO算法(简称PSO-CUDA)的伪代码如下所示. Algorithm PSO-CUDA1: Initial Swarm in CPU2: Set TPB as threads per block,BPG as blocks per grid3: Fori←1 to Iterations:4:cuda.to_device(Swarm) //拷贝种群至GPU5: @cuda.jit //添加JIT修饰符6: Kernel,TPB〛 //调用核函数完成粒子评价、更新个体历史最优解、粒子升级7:cuda.copy_to_host(Swarm) //拷贝种群回CPU8: Check and Update Gbest //更新全局最优解9: Return the bestPosition and Fitness 其中:Kernel为GPU核函数,TPB为线程块大小,值为1 024,BPG为网格大小,其值由种群粒子数除以TPB向上取整得到.调用Kernel的执行配置为,表示GPU并行启动TPB*BPG个线程. PSO-CUDA算法分配至GPU中的计算任务主要由Kernel控制,考虑到GPU的逻辑运算能力不及CPU,如何合理为GPU分配计算任务、避免复杂逻辑是算法设计的关键.按照标准PSO算法逻辑,种群中个体升级都需要当前Gbest,但PSO-CUDA中的Gbest更新于CPU中完成、个体升级于GPU中完成,这将导致个体升级过程中不可避免地存在一次数据拷贝. 为解决这一问题,PSO-CUDA算法将Kernel核函数中的粒子升级步骤前置,使当代粒子直接利用上代得到的Gbest进行升级(首次迭代除外),以此减少数据拷贝的时间开销.PSO-CUDA算法中Kernel的流程如下所示. Kernel(粒子升级、评价粒子、更新个体历史最优解)1: Launch threads as the number of BPG*TPB2: AssignSwarm to threads3: For eachParticle in thread (Parallelly) do:4: Whilet!= 0: //避免首次迭代中的粒子升级5: UpdateVelocity and Position //粒子升级7: Evaluate Particle //粒子评价8: Check and UpdatePbest //更新个体历史最优解 种群拷贝至GPU后被分配至不同线程,每个线程将独立地调用Kernel核函数进行并行计算.Kernel流程可概括如下:1)粒子升级;2)粒子评价;3)更新个体历史最优解.Kernel完成上述处理后,将种群拷贝至CPU完成后续步骤. 实验旨在通过对比PSO算法与PSO-CUDA算法在同条件下的耗时,验证后者加速效率. 实验环境:CPU为Intel(R) Xeon(R) Gold-6130H 2.10 GHz,GPU为Tesla P100 16 GB,CUDA版本为11.4,操作系统为Ubuntu 18.04. 为进行充分验证,实验在不同粒子数、维数、测试函数下进行:粒子数P取值为10、100、1 000、4 000;维数D取值为10、100、1 000、5 000,测试函数边界为[-10,10]D,迭代次数Iterations为100.实验独立运行10次,实验结果取10次结果的均值. 为体现公平性与普适性,本实验选取群体智能算法性能测试常用的四个基准测试函数,其中,Sphere函数是常用的新算法的标准测试函数,其特点是全局最优解唯一,由D个定义域相同的自变量求平方和得到[21];Rosenbrock函数也称山谷函数或香蕉函数,是基于梯度的优化算法的一个流行测试函数,其函数图像呈现为单峰,全局最小值位于图像中最低点,但即使这个最低点很容易找到,其收敛到最低限度也比较困难[22];Rastrigin函数基于DeJong函数,存在多个局部最优解,增加了一个余弦调制传递函数来产生频繁的局部最小值,其特点是函数极小值出现的位置是有规律的,常用于解决一些规律性问题[23];Schwefel函数同样存在多个局部最优解,很容易引导算法陷入局部最优[24].测试函数表达式如表1所示. 表1 测试函数及表达式Table 1 Test functions and formulas 实验结果如表2和图1所示,其表明: 表2 算法耗时表Table 2 Algorithm time table 图1 算法耗时图Fig.1 Algorithm time graph 1)当D和P较小时,如[D,P]=[10,10]、[10,100]、[100,10],PSO算法的计算速度快于PSO-CUDA算法.这种现象主要是因为CPU主频高、Cache大,当计算规模较小时,CPU的浮点运算比GPU表现更好[25].此外CUDA core的启动和终止、数据拷贝等也会造成时间开销,故在计算规模较小时,出现CUDA程序计算速度慢于CPU程序的情况. 2)随着D和P的增大:D=10时,PSO-CUDA算法的速度从P=1 000开始快于PSO算法;D=100时,PSO-CUDA算法的速度从P=100开始快于PSO算法;D≥1 000时的所有配置组,PSO-CUDA算法都体现出较好的速度优势.[D,P]=[100,4 000]时PSO-CUDA算法的速度优势最大,达到PSO算法的3.44倍. 在PSO算法并行计算提速需求下,本文提出了基于GPU和Python的PSO算法,将计算量较大的粒子升级、粒子评价、更新个体历史最优解进行GPU加速,经实验验证, PSO-CUDA算法在维数和粒子数较小时速度表现差于PSO算法,PSO-CUDA算法的速度优势随着维数、粒子数的增加而逐渐体现,并在维数为100、粒子数为4 000时达到了PSO算法3.44倍的加速效果. 本文虽然研究了基于GPU的PSO加速问题,但由于群体智能算法的复杂性,该问题仍然是开放性的,仍有一些可研究的问题,例如:改变PSO算法的并行层面,从维度、核函数等方面并行;在其他版本的PSO算法中验证GPU并行的有效性;把本文的并行方法扩展应用于其他群体智能算法中.2 基于GPU和Python的改进粒子群优化算法
2.1 PSO-CUDA算法

2.2 Kernel核函数

3 实验
3.1 实验环境及参数设置

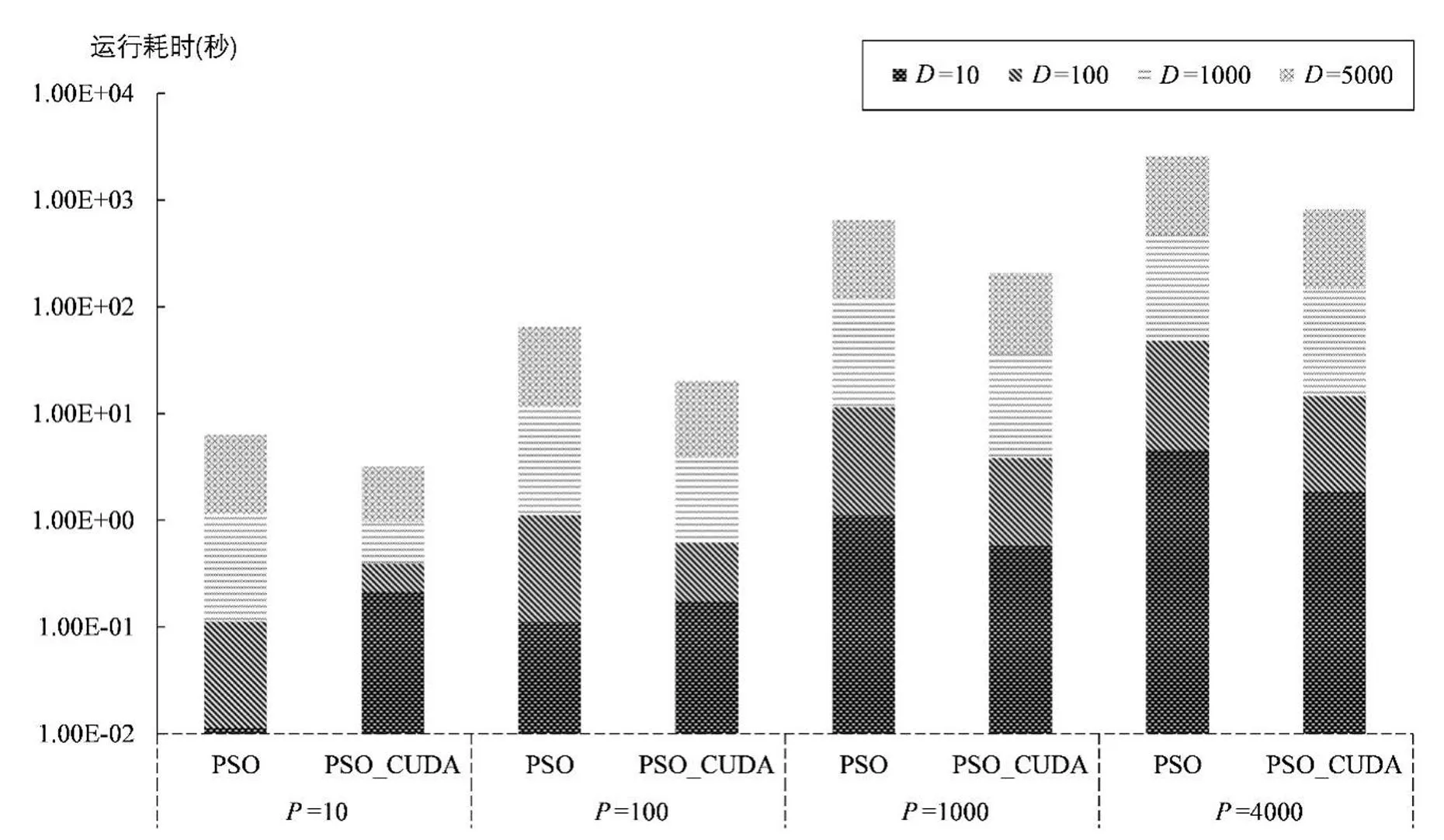
3.2 实验结果与分析

4 总结

