亏格不为1的二次可逆LV系统的极限环分支*

吴莎， 吴奎霖

贵州大学数学与统计学院， 贵州 贵阳 550025

自从Hilbert第16 个问题被提出以来，极限环个数的问题就成为平面微分系统定性理论研究的热点问题之一.我们研究具有小扰动项的多项式可积系统：

其中M(x，y)是对应H(x，y)的积分因子.用环性表示多项式系统在小扰动下分支出的最大极限环个数.研究Abel积分I(h)孤立零点个数问题涉及弱化的Hilbert第16问题.系统（1）的后继函数可表示为

其中d(h，θ)定义在流的一个横截线段上，这个流由哈密顿函数H=h给出.称Mk(h)为k阶Melnikov 函数.未扰可积系统(1)ε=0的周期环域在扰动下产生极限环个数的上界等于d(h，ε)中第一个非零的Melnikov函数Mk(h)的零点个数.

在文献（Zoladek， 1994）里，中心在原点的平面二次系统分为以下几类：

1 预备知识

我们借助切比雪夫系统性质证明主要结果.首先介绍了切比雪夫系统的定义以及相关的一些结论.

定义1 令f0(x)，f1(x)，…，fn-1(x)是开区间L⊂R上的解析函数.

（a）如果任何非平凡线性组合

在L上至多有n- 1个孤立零点，则(f0(x)，f1(x)，…，fn-1(x))是L上的一个切比雪夫系统（简称，T-系统）.

（b）如果对于任意的k= 1，2，…，n，(f0(x)，f1(x)，…，fk-1(x))是L上的一个切比雪夫系统，则称(f0(x)，f1(x)，…，fn-1(x))是L上的一个完全切比雪夫系统（简称， CT-系统）.

（c）如果对于任意的k= 1，2，…，n，所有非平凡线性组合

在L上至多有k- 1 个孤立零点（计算重数），则称(f0(x)，f1(x)，…，fn-1(x))是L上的一个广义的完全切比雪夫系统（简称， ECT-系统）.

显然，ECT-系统是CT-系统，反之不成立.ECT-系统考虑零点重数，但CT-系统不考虑零点重数.下面介绍ECT-系统的一些性质.

定义2 令f0(x)，f1(x)，…，fn-1(x)是开区间L⊂R 上的解析函数.(f0(x)，f1(x)，…，fn-1(x))在x∈L处的连续朗斯基行列式为

引理1（Borwein et al.， 1995） (f0，f1，…，fn-1)是L上的一个ECT-系统，当且仅当对任意的k=0，1，…，n- 1，

2 定理1的证明

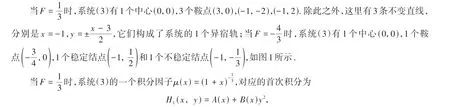
图1 系统（3）的局部相图Fig.1 The local phase diagram of system （3）

其中

接下来借助数学软件来证明以下引理.

通过计算我们知道：ψ0(0)是ψ0(v)在(0，1)上的最大值；当v≈0.570 0 时，ψ1(v)在(0，1)上有最小值7.399 3 × 1021；对于ψ2(v)，由Sturm定理可知其在(0，34 - 1)上没有零点.所以，对于任意u∈(0，34 -1)，3 个朗斯基行列式W[L0(v，z)，L1(v，z)，L2(v，z)]，W[L1(v，z)，L2(v，z)]，W[L2(v，z)]在(0，34 - 1)上无零点.从而可知{ℓ0(v)，ℓ1(v)，ℓ2(v)}是开区间(0，34 - 1)上的一个ECT-系统.

定理1的证明 由引理2，引理4和引理5可得定理1.