Koszulity of the operad AsLC■Dend*

, ,

1. School of Information Engineering and Artificial Intelligence, Lanzhou University of Finance and Economics, Lanzhou 730101, China

2. School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, China

3. Gansu Provincial Research Center for Basic Disciplines of Mathematics and Statistics, Lanzhou 730070, China

4. School of Mathematics and Statistics, Qinghai Nationalities University, Xining 810007, China

5. Cuiying Honors College, Lanzhou University, Lanzhou 730000, China

Abstract: The Koszulity of the operad AsLC ■Dend in terms of the method of rewriting systems is proven, where AsLC■Dend is the Manin black product of the linear compatible operad of the associative As and the dendriform operad Dend.

Key words: operad; Koszulity; linear compatible operad; dendriform operad; Manin black product

1 Introduction

An important property of derivations and its generalizations is that their linear closure allows them to form a vector space further a Lie algebra, which cann't be expected for other operators or operations.Hence it is natural to discuss that given an operation, what condition can make its some properties pass to the linear combination of multiple copies of this operation.Such a condition is called a linear compatible condition, which emerged in the pioneer work of Magri, applying for the Lie bracket.Subsequently, this condition was generalized in many other places, including operad theory, and a lot of algebraic structure appeared by this condition.

There have been many exciting theories in the last century, andK-theory is one of them.In algebraicK-theory, periodicity questions led to the construction of diassociative algebra, and the explicitation of the homology of diassociative algebra led to the discovery of the Koszul dual structure, called dendriform algebra later.Using operad theory, dendriform algebras can be encoded by dendriform operad.The dendriform structure models the noncommutative shuffles, and dendriform operad is closely related to planar binary trees.Moreover,the dendriform operations "split associativity".Therefore the notation of dendriform algebras is used extensively in combinatorial algebra, theoretical physics, algebraic topology and other domains.

Koszul duality is a part of operad theory.It was first developed at the level of associative algebras by Stewart Priddy in the 1970s.Later this duality was extended to algebraic operads.One of the interesting result about it, is that the duality between Lie algebras and commutative algebras in rational homotopy theory coincides with the Koszul duality theory between the operad encoding Lie algebras and the operad encoding commutative algebras.The operadic application of Koszul duality theory to homotopical algebra is a profound generalization of Dan Quillen and Dennis Sullivan's thought.

In this paper, the main result is that the operad of the Manin black product AsLC■Dendis Koszul, where AsLCis the linear compatible operad of the associative Asand Dendis the dendriform operad.The paper is organized as follows.In Section 2, we recall the necessary concepts, including the linear compatible operad AsLCof the associative operad As, the operad Dendof dendriform algebras and the Manin black product of operads.Section 3 is devoted to prove that the operad AsLC■Dendis Koszul(Theorem 2), in terms of the convergency of the rewriting system ΠAsLC■Dendinduced from the operad AsLC■Dend(Theorem 1).

2 The operad AsLC■ D end

In this section, we are going to introduce the operad AsLC■Dend.Let us first recall the necessary concepts.

Definition 1(Loday et al., 2012) A nonsymmetric operad is an arity graded vector space P ={P0,P1,…}equipped with an element id ∈P1and composition maps:

be two P-algebras such thatμiandνiare the corresponding binary operations for 1 ≤i≤k.Denoteηi≔αμi+βνifor someα,β∈k.The pairA,Bare called linearly compatible ifC=(V,η1,…,ηk) is a P-algebra for any choice ofαandβ.This is equivalent to requiring thatCis a P-algebra forα=β= 1.

When the operad P is the associative operad As, there is an equivalent description of linearly compatible Asalgebras.

Definition 3(Odesskii et al., 2006; Odesskii et al., 2008) LetVbe a vector space over k, andA1=(V, ∘1)andA2=(V, ∘2) be two As-algebras.The pairA1,A2are linear compatible if

Denote the associative operad Asby As= As(E,R), where

Consider two copies of As

where

and

Denote byRLthe singleton set of the relation in Eq.(1).

Definition 4 Define the linear compatible operad AsLCof Asby

where T (E1⊕E2) is the free operad onE1⊕E2andR1∪R2∪RLis the operadic ideal generated byR1∪R2∪RL.

In terms of the operad AsLC, theAandBin Definition 2 are linear compatible if and only if the vector spaceVis an AsLC-algebra (Strohmayer, 2008).

Inspirited by algebraicK-theory, Loday(1993) introduced the concept of dendriform algebras.

Definition 5(Loday, 1993) LetVbe a vector space with two bilinear products denoted by ≺ and ≻.Then(V, ≺, ≻) is called a dendriform algebra if

Denote by Dendthe operad of dendriform algebras.Now we introduce the notion of Manin black product.

Definition 6(Fard et al., 2005; Vallette, 2008) Let P = P(E,R) and Q = Q(F,S) be two finite generated binary quadratic nonsymmetric opeards with relations

and

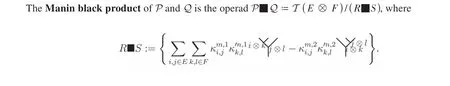
3 Koszulity of the Manin black product A sLC■D end

In this section, we first induce a rewriting system from AsLC■Dendand then show that it is convergent.As an application, we obtain that the operad AsLC■Dendis Koszul.

3.1 The rewriting system from AsLC■ Dend

It follows from Definition 6 that the Manin black product AsLC■Dendhas four operations:

where ∘I, ∘IIare the two binary operations of the linear compatible operad AsLinof the associative operad Asand≺, ≻ are the two binary operations of the dendriform operad Dend.For convenience, we denote

We assume ∘II> ∘Iand ≻ > ≺.Then ∘4> ∘3> ∘2> ∘1by degree lexicographical order.Using the pathlexicographical order (Loday et al.,2012), we obtain the following nine rewriting rules of the operad AsLC■Dend:

Denote this rewriting system by ΠAsLC■Dend.Notice that the monomial in the left hand side of each rewriting rule is the leading monomial in the corresponding relation, with respect to the path-lexicographical order.Using the above rules, we have the following rewriting processes

which will be used later.

3.2 The Koszulity of AsLC■ Dend

In this subsection, we show that the rewriting system ΠAsLC■Dendfrom the operad AsLC■Dendis convergent.Let us begin with the following key concept of rewriting systems(Baader et al.,1998).

Definition 7 A rewriting system Π is called

(a) terminating if there is no infinite chain of one-step reductionsf0→Πf1→Πf2→Π…;

(b) confluent (resp.locally confluent) if every fork (resp.local fork) is joinable;

(c) convergent if it is both terminating and confluent.

A well-known result on rewriting systems is Newman's Lemma (Baader et al.,1998).

Lemma 1 A terminating rewriting system is confluent if and only if it is locally confluent.Now we are ready for our first main result.

Theorem 1 Let ∘II> ∘Iand ≻ > ≺.With respect to the path-lexicographical order, the rewriting system ΠAsLC■Dendinduced from the operad AsLC■Dendis convergent.

Proof Since the path-lexicographical order is a well order(Loday et al.,2012), the rewriting system ΠAsLC■Dendis terminating.By Lemma 1, we are left to show that ΠAsLC■Dendis locally confluent.There are sixteen ambiguities in the rewriting system ΠAsLC■Dend.

Among the local forks of the above ambiguities, eight are known to be confluent by the convergency of the rewriting system of dendriform algebra:

L1，L3，L5，L6，L9，L10，L13，L15.

Hence we just need to check the cases of

L2，L4，L7，L8，L11，L12，L14，L16.

CaseL2.On the one hand,

On the other hand,

So the local fork from the ambiguityL2is confluent.

CaseL4.We have

and

Hence the local fork of the ambiguityL4is confluent.

CaseL7.We get

and

which shows the local fork corresponding the ambiguityL7is confluent.

CaseL8.On the one hand,

On the other hand,

hence the local fork of the ambiguityL8is confluent.

CaseL11.We have

and

Hence the local fork of the ambiguityL11is confluent.

CaseL12.The confluence of the local fork ofL12is by

CaseL14.By direct computation, we have

and

So the local fork of the ambiguityL14is confluent.

CaseL16.The confluence of the local fork fromL16follows from

and

This completes the proof.

As an application of the above theorem, we obtain the Koszulness of the operad AsLC■Dend.

Theorem 2 The operad AsLC■Dendis Koszul.

Proof It follows from Theorem 1 and Theorem 8.1.1(Loday et al., 2012).