基于时域最小残值法求解含间隙非线性气动弹性系统的半解析解*

秦英泉， 刘祚秋， 刘济科， 刘广

1.中山大学航空航天学院，广东 深圳 518107

2.深圳市智能微小卫星星座技术与应用重点实验室，广东 深圳 518107

近几十年中，对含非线性因素的机翼气动弹性响应进行了大量的研究（杨超等， 2018；杨智春等， 2016）。机翼系统中的非线性因素通常可以分为气动力和结构非线性，气动力非线性来自于空气来流（Gupta et al.， 2019），结构非线性来自于结构的大变形（齐念等， 2013）或者是材料的非线性本构关系（Darabi et al.， 2019）等。此外，机翼在加工和安装过程中的容限误差，或者是控制面铰链的松动都会引入间隙非线性（Shi et al.， 2023）。理论分析以及风洞试验都表明，系统存在上述非线性因素时，若来流速度超过临界速度机翼就会产生极限环振荡（Liu et al.， 2018）。

分析非线性气动弹性系统周期解的方法主要有数值法和解析法。因数值方法的局限性，学者更加关注解析或半解析法。常见的的解析或半解析方法，如谐波平衡法（Miguel et al.， 2020）、同伦分析法（Liao et al.， 2004）和增量谐波平衡法（Liu et al.， 2018）等，都能够成功获得非线性系统的周期解。但是由于间隙非线性的非光滑性，上述半解析方法在实施之前都需要先对间隙非线性进行光滑化处理（Liu et al.， 2012）。此类光滑化处理或多或少会引入一些额外的模型误差。且含间隙非线性的气动弹性系统还属于自激系统，这意味着对于处于周期振动状态的机翼系统，其振动的频率是未知的（Liu et al.， 2012；Liu et al.， 2018）。这些进一步增大了求解含间隙非线性的气动弹性系统半解析周期解的难度。

本文提出了一种新的求解非线性系统的半解析方法，即时域最小残值法（Liu et al.， 2021a；Liu et al.，2021b；Liu et al.，2022）。该方法通过将含间隙非线性的气动弹性系统的半解析解求解问题转化为最小值优化问题，然后在时域节点上展开迭代求解。由于该方法属于时频混合方法，并且是直接对含间隙非线性的气动弹性系统的控制方程进行求解，因此无需对非光滑区域进行光滑处理，得到的半解析解具有更高的精度。

1 二元机翼模型的运动方程

图1为大展弦比的机翼模型，仅考虑模型在俯仰和沉浮方向的运动（Liu et al.， 2012）。图中，b为机翼半跨的长度；h为机翼在沉浮方向的位移，取向下为正；α为机翼俯仰角度，取抬头为正；E为机翼的弹性轴。ahb为弹性轴E到机翼中心的距离，xαb为机翼质心位置G到弹性轴E的距离。

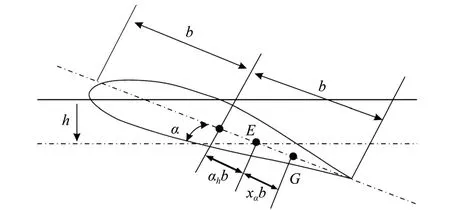
图1 二元机翼模型Fig.1 Sketch of the two-dimensional airfoil

假设机翼在亚音速的不可压缩流中运动，根据第二类Lagrange 方程，建立如下的气动弹性系统运动方程（Liu et al.，2018）

式中h，α上的点代表对无量纲时间t'的导数，t'=Vt/b，V为来流速度，t为真实运动时间。无量纲沉浮位移h1=h/b；rα为机翼绕弹性轴E的回转半径；ζh和ζα为机翼在沉浮和俯仰方向的阻尼比。无量纲频率比-ω=ωh/ωα，ωh和ωα为机翼沉浮和俯仰方向的固有频率。U=V/bωα为无量纲来流速度；μ为单位长度的机翼与空气密度的比值；m是单位长度的机翼质量。考虑俯仰方向存在间隙非线性，俯仰方向的非线性刚度M(α)为

M(α)与α的关系如图2 所示。图中δ为间隙大小，Mf为图中间隙对应的斜率。

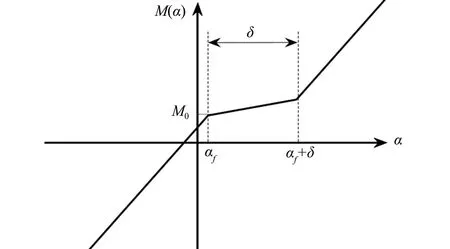
图2 M(α)与α的关系Fig.2 Sketch of M(α) versus α

根 据Theodorsen 气 动 理 论（Theodorsen，1949），方程（1）中的升力CL(t)为

式中ei，fi(i= 0～7)及gi(i= 0～5)的表达式在附录中给出。引入x=[h，α，y]T，将方程（5）化为

式中非线性向量F(x) =[0，f7M(α)，0]T，系统质量矩阵为

刚度矩阵为

2 时域最小残值法

2.1 最小值优化问题

时域最小残值法最早是由刘广等提出，是一种针对强非线性系统的半数值半解析方法（Liu et al.， 2021a；Liu et al.，2021b；Liu et al.，2022）。本文也将采用时域最小残值法来求解方程（5）所示的含间隙非线性气动弹性系统的周期解。对于方程（5）所示的周期解，可以展开为傅里叶级数

其中xj(t)表示第j个自由度的位移，aj0是常数，cjk与sjk是待定的正余弦谐波系数，ω是和来流速度相关的未知频率。而求解方程（6）的半解析周期解，本质为求解未知参数

当确定参数a后，代入方程（7）中，即获得了系统的半解析周期解。需要注意的是，在实际求解过程中，方程（7）中的级数是不可能取无穷项的，因此截取方程（7）的前N项作为系统的近似解，即

方程（8）和（9）的近似级数解代入系统（6）所获得的残差，显然不能在整个时域上恒等于0。此时的系统残差为

虽然不能使残差R在整个时域内都为0，但仍可以通过选取合适的参数a使得残差R在一个周期t∈[0，T]内尽可能小。自此，关于含间隙非线性气动弹性系统的半解析周期解求解问题被转化为最小值优化问题，即

式中ℏ(a，t)为非线性目标函数，A是未知参数a的可行域。

2.2 增强的响应灵敏度法

对于方程（11）的最小值优化问题，可以通过增强响应灵敏度法来迭代求解。即选定一个合适的迭代初值a()0，令

上述正则化也叫增强的正则化，该响应灵敏度法也被称为增强的响应灵敏度法。

3 数值算例

对于方程（6）所描述的系统，根据Hopf分岔理论（Marsden， 1976；Hassard et al.，1981），当来流速度U超过临界颤振速度Uf= 6.285 1 时，系统将会失去稳定性。本算例首先考虑U= 0.8Uf的情况，此时系统将会产生稳定的极限环，其近似周期解可被展开为如方程（8）的傅里叶级数，以第一个自由度为例，有

对第二和第三个自由度进行类似的操作，并将所得位移、速度和加速度函数代入方程（6），则含间隙非线性的气动弹性系统半解析解求解问题就被转化为方程（11）所示的最小值优化问题。即，寻找一组未知参数

图3 给出了N= 30，U/Uf= 0.8 时系统的相图。图3 中，（a）为沉浮方向的相图，（b）为俯仰方向的相图；黑点表示4 阶龙格-库塔法获得的数值解，红线和蓝线为时域最小残值法获得的半解析解。从图中可以看出，数值解和时域最小残值法获得的半解析解吻合非常好，这意味着时域最小残值法获得的结果有着较高的精度。此外，当U/Uf=0.8 时，系统两个方向的相图均不关于原点对称，这表明方程（8）的半解析周期解同时存在奇次谐波和偶次谐波。表1 给出了N= 30、U/Uf= 0.8 时该半解析周期解的谐波系数及振动频率。图4给出了含间隙的气动弹性系统的时程图。和图3类似，红线和蓝线分别为时域最小残值法获得的沉浮方向和俯仰方向的半解析解。时程图进一步验证了时域最小残值法获得的半解析解和龙格-库塔法的结果吻合得非常好。

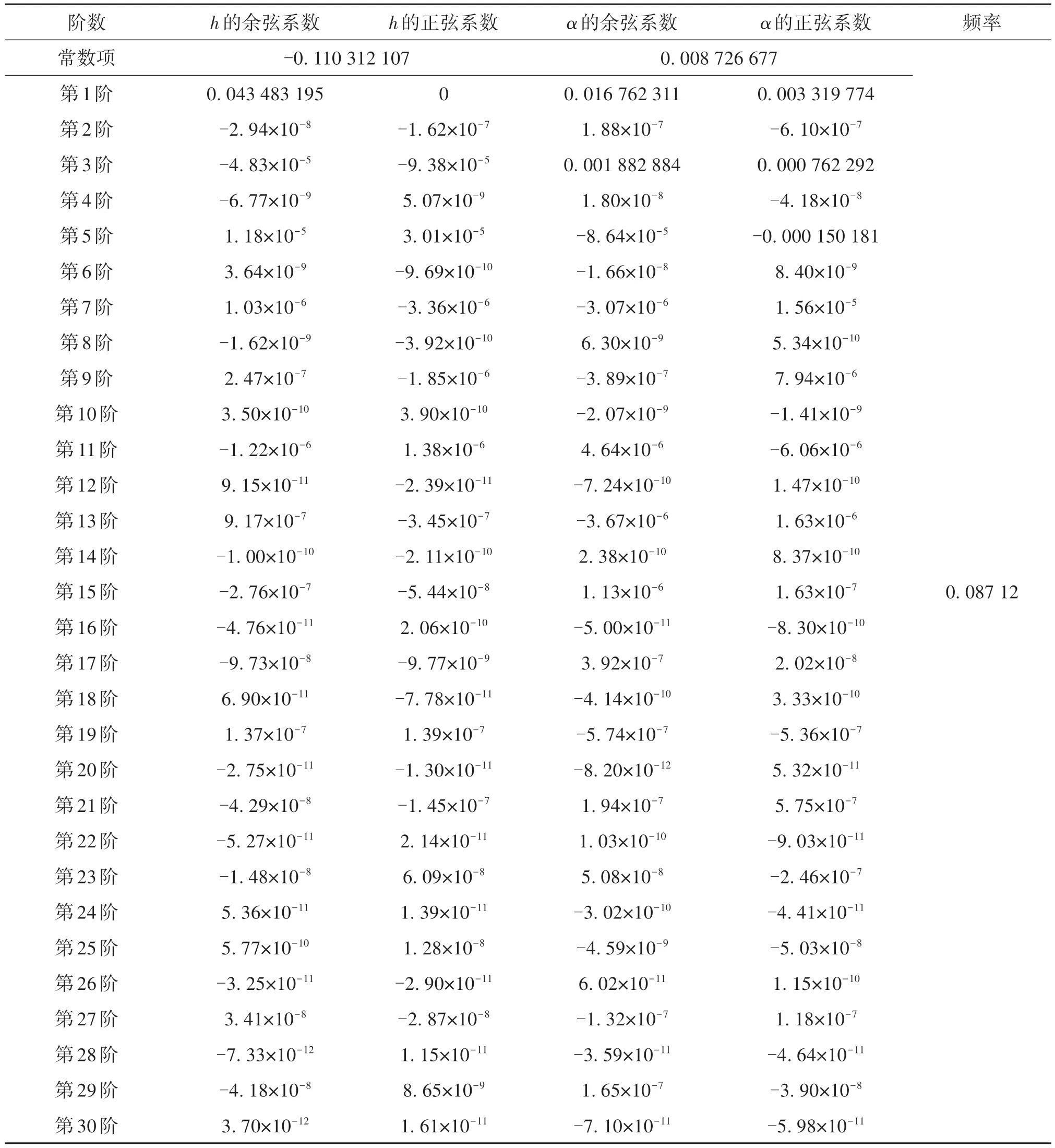
表1 N = 30，U/Uf = 0.8时的谐波系数与振动频率Table 1 The Harmonic coefficient and vibration frequency at N = 30，U/Uf = 0.8

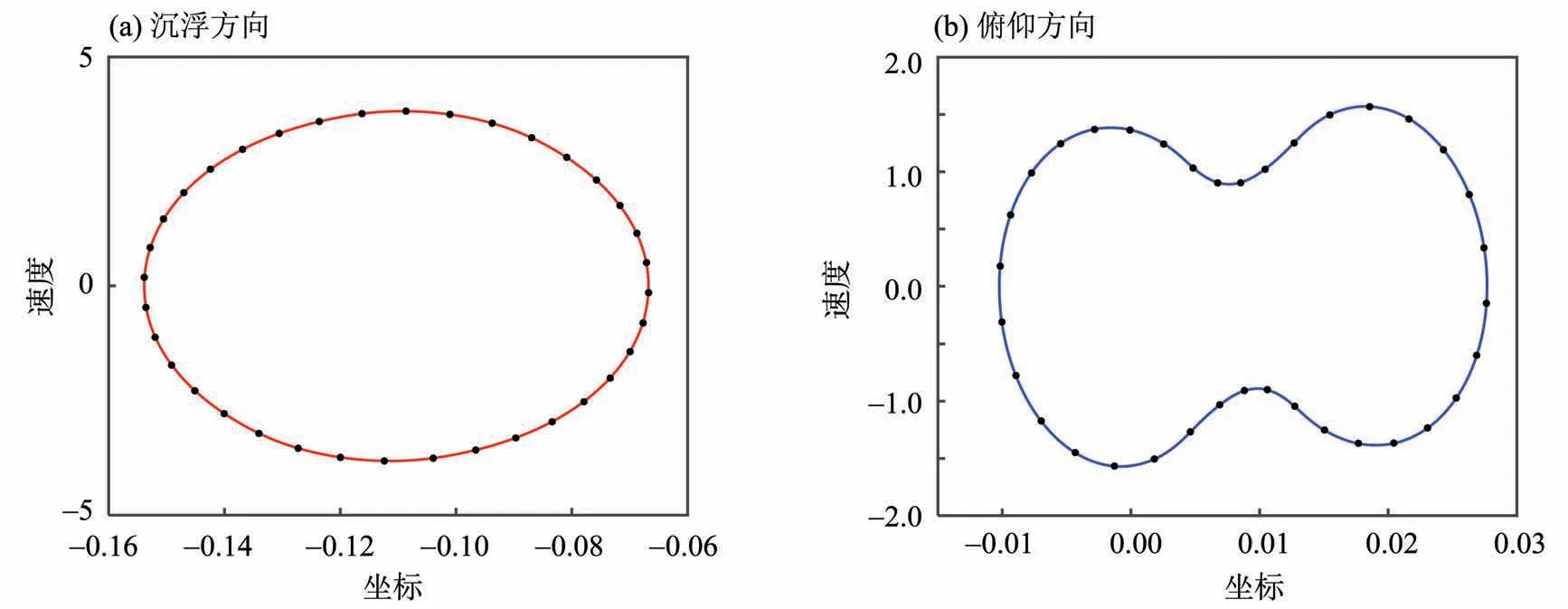
图3 U/Uf = 0.8时系统的相图Fig.3 The phase of the system at U/Uf = 0.8

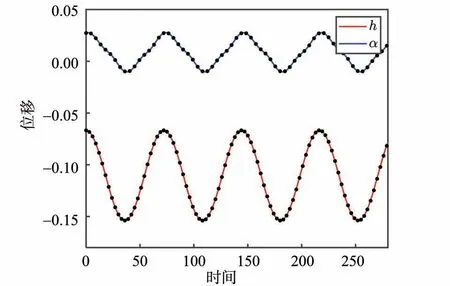
图4 U = 0.8Uf时系统的时程图Fig.4 The time histories of the system at U = 0.8Uf

图5给出了不同谐波数的俯仰方向相图。图中红点为截取项数N=1 时对应的极限环，虚线、绿色实线和蓝色实线分别表示N= 5，20，30 时俯仰方向的相图，而黑点则表示4 阶龙格-库塔法的结果。从图中可以看出，当仅保留1阶谐波时，时域最小残值法虽然能够收敛，但结果误差非常大。随着保留的谐波数逐渐增加，半解析解的精度也逐渐升高。在图5 的局部放大图中，当保留5 阶谐波时，时域最小残值法获得的半解析解已经可以收敛到正确解上，但和精确解仍有区别。当保留20 或30 阶谐波时，半解析解和数值解完全重合。这意味着当保留的谐波数增加到一定数量时，谐波数的增加对精度的提升已经不大，但更多的谐波数会显著影响求解的效率。

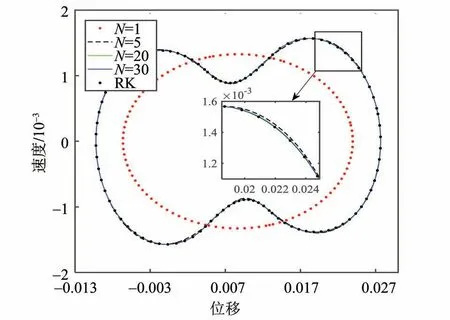
图5 保留不同数目的谐波获得的俯仰方向相图Fig.5 The phase of the system with different order of harmonics

为了定量分析截断的谐波阶次对精度的影响，将获得的半解析解代到控制方程，绘制系统的残差曲线。图6 为N= 5，20，30 时两个自由度的残差曲线。其中，红线和黑线分别为沉浮方向和俯仰方向的残差曲线。从图中可以看到，N= 5 时系统的残差为10-5的量级；N= 20时，系统残差约为N= 5 时的一半量级；N= 30 时，残差减小到10-6的量级。这说明保留的谐波越多，对应的半解析解有更高的精度；但当保留的谐波数达到一定的数值之后，谐波阶次对精度的提升有限。

此外，俯仰方向的残差曲线中有几个尖峰，这是由于方程（8）所示的半解析解采用傅里叶级数作为基函数。对于系统（6）而言，M(α)存在与α有关的不光滑区域。当采用截断的傅里叶级数作为系统的近似解析解时，将会在非光滑区域的转折点附近出现无法避免的Gibbs 现象。Gibbs 现象的存在意味着，以增加截断谐波的阶次来提升近似解析解的精度，需要付出巨大的计算代价。即必须保留足够多的谐波，才能微量地提升半解析解的精度。这一性质是由系统的非光滑属性本身决定的，和本文采用的时域最小残值法无关。

对于来流速度U/Uf= 0.39 时的含间隙的气动弹性系统（6），当系统的未知参数ai取不同的初始迭代值时，时域最小残值法可能会获得不同的结果。图8给出了以另一组迭代初值获得的俯仰方向的相图。对比图8 和图7 可以看到，两者的相图是反对称的。这意味着系统的振动形态和系统的初始状态相关，不同的初始状态将会导致系统进入不同的稳定极限环，从另一方面体现了含间隙的气动弹性系统具有丰富的非线性性质。

图7 U = 0.39Uf时系统的相图Fig.7 The phase of the system at U = 0.39Uf

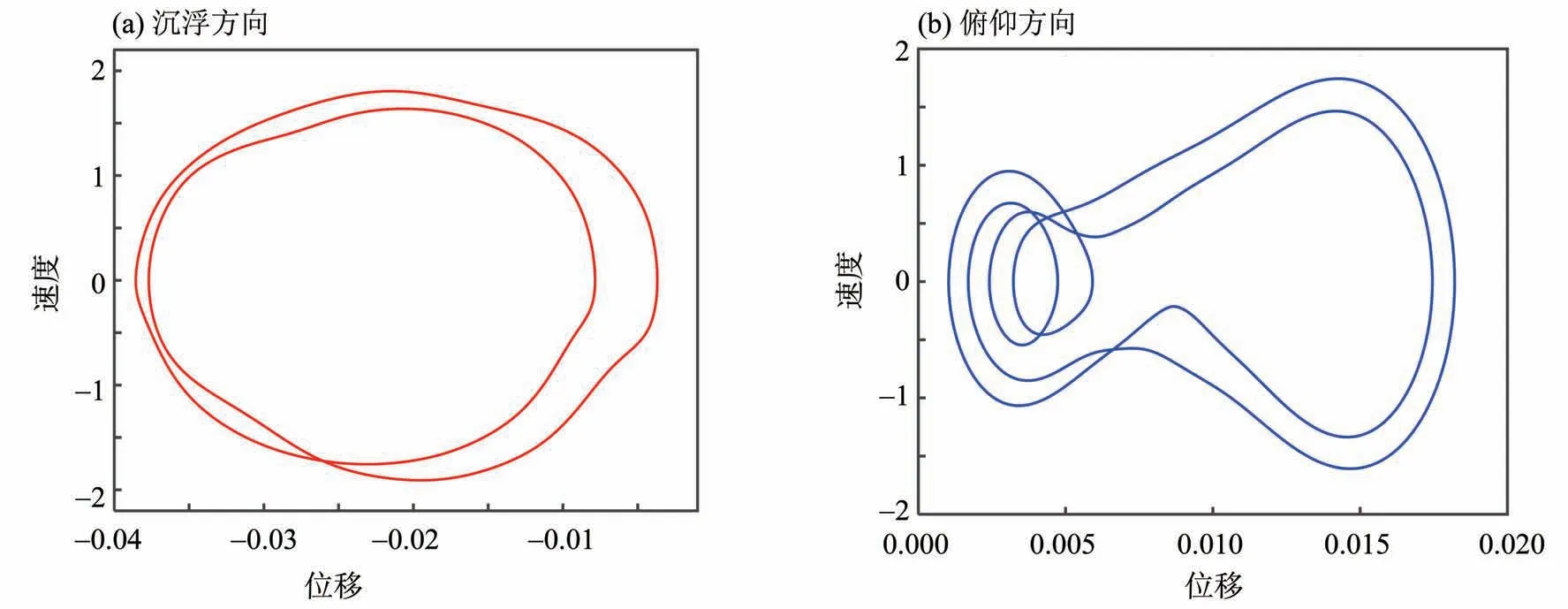
图8 不同初始迭代值时系统的相图Fig.8 The phase of the system with different initial iteration values

4 结 论

本文提出了一种新的求解含间隙非线性气动弹性系统的半解析方法，即时域最小残值法。通过该方法获得了来流速度为U/Uf= 0.8 和U/Uf=0.39时系统的半解析解，并和数值法获得的结果进行了对比，得到以下结论：

（1）时域最小残值法获得的半解析解和数值法的结果吻合的非常好；

（2）即便只考虑1阶谐波，时域最小残值法的迭代也可以收敛。此外保留的谐波越多，获得的结果精度越高；

（3）时域最小残值法从不同的初始迭代值出发，可能收敛到系统不同的极限环。