剪切过程中钙质砂的颗粒破碎与能量演化*

高雪， 高燕，2， 孙可天， 史天根

1.中山大学地球科学与工程学院，广东 珠海 519082

2.南方海洋科学与工程广东省实验室（珠海），广东 珠海 519082

钙质砂作为一种生物成因的海源砂，其碳酸钙含量超过90%，在我国南海诸岛广泛分布。相比硅质砂，钙质砂具有多棱角、颗粒形状极不规则、疏松多孔、易破碎、易压缩等特性（张家铭等，2005；陈海洋等，2005；吴京平等，1997；汪轶群等，2018；孙吉主和汪稔，2003）。近年来我国在南海进行了大量的吹填岛礁工程，其工程建设采取因地制宜、就地取材的方针，岛礁建设吹填部分以珊瑚钙质砂为主（叶剑红等，2019；高燕等，2022），由于钙质砂颗粒的破碎性导致其工程力学性质与经典土力学不符，因此研究钙质砂的破碎性具有重要的工程意义。

我国对于钙质砂的试验研究主要是从20 世纪70 年代末开始，有学者对钙质砂颗粒形状及内孔隙进行了研究（吴京平和楼志刚，1994；陈海洋等，2005；朱长歧等，2014）；国内外学者对钙质砂开展了大量的室内试验，主要有直剪试验、三轴试验、压缩试验、循环剪切试验等（孙吉主和汪稔，2003；Georgoutsos et al.，2004；张 家 铭，2008；Donohue et al.，2009；Shahnazari and Rezvani，2013；毛炎炎等，2017；何建乔等，2018，王刚等，2019，王伟光，2020），分析钙质砂的颗粒破碎对其抗剪强度及受力变形特性的影响。然而现有试验手段很难在试验过程中同时获得接触力与颗粒运动信息、跟踪颗粒破碎所耗散的能量，因此，离散元（DEM）数值模拟成为了进一步开展微观力学机制研究的重要手段（Cundall and Strack，1979；王伟光，2020）。

使用DEM 进行颗粒破碎的数值模拟主要有2种方法：一是确定破坏准则，当颗粒达到破坏条件时采用多个子颗粒替代母颗粒的方法（Lobo-Guerrero and Vallejo，2005），但是该方法在替换颗粒过程中，质量很难守恒，颗粒间的重叠亦会导致接触力过大，与真实情况不符（刘苏，2018）；另一种是由接触黏结形成可破碎的团粒（Russell，2009），该方法可以生成较复杂形状的颗粒，并且更利于模拟颗粒破碎的演化过程，但该方法计算过程更为繁琐，模拟颗粒数较多的情况时需花费大量时间。Cheng et al.（2003）利用PFC3D对可破碎团粒进行了不同应力路径下的三轴试验数值模拟，表明颗粒破碎对砂土硬化以及体积压缩有重要影响。Lobo-Guerrero（2006）通过PFC2D对比可破碎材料与不可破碎材料，认识到颗粒破碎可导致永久的变形。Bolton et al.（2008）对可破碎颗粒与不可破碎颗粒混合试样进行三轴仿真试验，发现了颗粒主要有3 种破碎方式。Wang et al.（2012，2013）和周博等（2014）分别通过三维与二维数值模型详细研究了可破碎砂土在剪切过程中颗粒破碎对能量耗散分配机制的影响，对比了小应变与临界状态下不同能量分量的演化差异。张家铭等（2015）用接触黏结模型连接的二维团簇粒模拟钙质砂颗粒，分析了沉桩过程中的颗粒破碎。张科芬等（2017）开展了不同破碎程度的颗粒材料的数值模拟，并与室内试验结果进行对比，揭示了颗粒破碎对于试样各向异性与级配演化的作用。王刚等（2021）建立了钙质砂离散元数值模型，并对其进行不破碎三轴剪切过程的数值试验，以分析颗粒破碎对钙质砂临界状态的级配演化的影响。

目前，国内外关于颗粒破碎数值模拟方面的研究已经比较成熟，但研究颗粒破碎与其系统内部能量耗散特性的联系却较少提及。Wang et al.（2012，2013）和周博等（2014）分析了能量耗散机制，但其认为砂土破碎演化中输入功主要通过摩擦耗散，颗粒破碎本身只耗散了极小一部分能量。而在钙质砂试验过程中颗粒破碎本身会引起能量耗散，汪轶群等（2018）基于三轴试验结果，分析了颗粒破碎对能量耗散等特性的影响，得出低围压情况下，颗粒破碎耗散能量不超过输入功的5%，而高围压情况下，只考虑摩擦耗散与同时考虑摩擦耗散与体积耗散，破碎耗能分别最大可达总输入功的25%和18%。因此，颗粒破碎本身所耗散的能量不可忽视。在前人研究的基础上，本文基于PFC2D软件，结合了Hertz 接触模型和平行黏结模型，建立钙质砂的离散元模型进行剪切试验的数值模拟，并分析剪切过程中颗粒破碎与能量演化的关系。

1 考虑颗粒破碎的离散元数值模型建立

本文采用离散元软件PFC2Dversion 4.0（particle flow code，美国Itasca 公司），模拟了200 kPa 围压下初始孔隙率为0.1（密砂）状态下的钙质砂剪切过程（陈庆等，2021）。模型为长方形试样，尺寸为8 cm×4 cm。颗粒的初始粒径范围为1～2 mm，粒径分布符合真实砂土的粒径分布规律（蒋明镜，2019；Kuhn and Bagi，2009），如图1 所示。颗粒间的接触模型采用Hertz-Mindlin 非线性接触模型，其剪切模量G=3 GPa，泊松比ν=0.2。颗粒破碎是影响钙质砂宏-微观特性的重要因素，为了更真实地反映剪切过程中钙质砂的颗粒破碎特征，本文接触模型中加入了平行黏结模型，平行黏结模型将两个颗粒通过一定宽度的胶结键黏结成簇，平行键可以承担一定的剪力、拉力以及弯矩作用（Itasca，2008）。本文参考周博（2014）的离散元模型，综合考虑了颗粒内部不均匀性和初始应变能，钙质砂试样的离散元模型生成流程如图2所示。

在平行接触模型中，子颗粒接触点的法向、切向强度以及黏结键的宽度都会影响到试样的整体强度（Wang and Yan，2012），因此为了得到合理的数值模拟参数，本文进行单颗粒压碎模拟，最终选取了2组典型的应力-位移曲线（图3），相应的平行黏结模型选用的强度为3×106和5×106N/m，分别对应高破碎性与低破碎性钙质砂颗粒。剪切过程中，赋予上、下墙一定的速度对试样进行剪切，达到设定的20%轴向应变（ε）后模拟结束。同时计算过程中通过PFC 内置的solve 命令使得平均不平衡力与平均接触力之比维持在一个较低的值，从而使试样始终保持准静态平衡条件（Kuhn and Bagi，2009）。数值模拟中的各参数取值见表1。

表1 双轴模型基本物理参数Table 1 Basic physical parameters of biaxial model

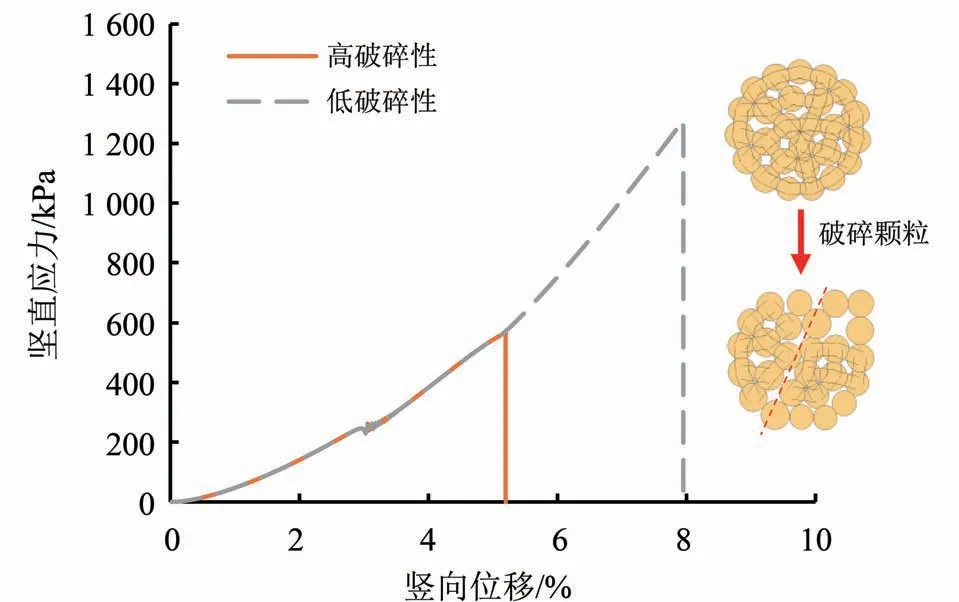
图3 单颗粒压碎模拟结果Fig.3 The results of single-particle compression by DEM simulations

破碎率是衡量颗粒破碎程度的重要指标，本文通过试样中颗粒平行粘结键断裂的数目来描述颗粒破碎的情况，破碎率（Br）定义为颗粒内黏结键断裂数与剪切初始平行黏结键总数目的比值式中Nbr为颗粒内黏结键断裂数，Npb0为剪切初始平行黏结键总数目。

2 能量表征参数及其计算方法

双轴试验的目的是了解能量在数值模型中是如何应用、存储和消散的。本文中颗粒系统的能量通过6 种相互独立的能量分量组成，即，边界功、摩擦功（能量耗散）、动能、应变能、阻尼能和破碎能，研究钙质砂剪切过程中颗粒破碎、能量演化与宏观变形的关系。鉴于本文剪切过程为准静态发展，因此不考虑动能的变化。边界功Ew是作用于土样边界的总功，表示为

其中，在非线性的Hertz-Mindlin模型中，kn和ks由构成颗粒材料的剪切模量G、泊松比υ、颗粒半径R͂和颗粒重叠量Un决定，

对于阻尼耗散，采用适合准静态模拟的局部非粘性阻尼器模型，阻尼能Ed是通过阻尼器耗散的能量，

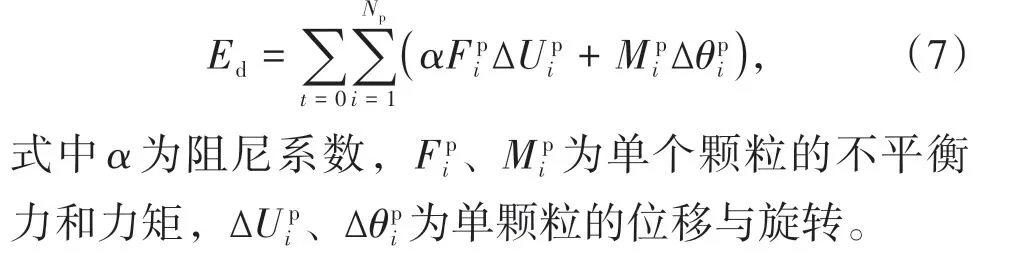
当平行黏结断裂时，储存在平行黏结中的弹性应变能会被释放出来，这部分能量损失被视为破碎耗能Ep，

式中Npb为平行黏结断裂个数，rpb为平行黏结半径比，r1、r2为颗粒半径，Fˉn，ti、Fˉs，ti、Mˉ3分别为法向、切向黏结力与力矩，kˉtn、kˉts为法向、切向黏结刚度。

根据能量守恒定律有，

3 钙质砂的剪切特性与能量演化特征

对钙质砂剪切试验的数值模拟分为高破碎率密砂（DH）和低破碎率密砂（DL）模拟。

3.1 应力-应变特征与颗粒破碎

钙质砂剪切数值模拟结果如图4 所示。DL 钙质砂的应力应变曲线和体积应变曲线分别表现出应变软化以及先剪缩后剪胀的密实砂土剪切的典型特征，DH 试样的体积应变始终呈现剪缩的趋势。

图4 密实钙质砂剪切过程中应力-应变与体积应变曲线Fig.4 The stress-strain response and volumetric strain response during shearing process of dense calcareous sands

剪切过程中颗粒破碎率的变化，随着剪切的进行，颗粒破碎程度增加，即使在临界状态下颗粒仍在发生破碎，这与试验结果相符合（图5）。DH 试样的破碎程度远大于DL 试样，二者的破碎速率在剪切后期都呈现出降低的趋势，颗粒破碎率增长的斜率明显降低，即说明随着剪切的进行，需要更大的能量输入才能继续产生颗粒破碎，表明剪切的不同阶段颗粒破碎的模式可能不同。随着颗粒破碎率的增加，钙质砂的峰值应力降低，应力应变曲线逐渐由应变软化向应变硬化转变，但临界状态下的残余应力却很相近。由于剪切过程中颗粒持续破碎产生细颗粒填充到试样原有的孔隙中，导致试样的剪胀性降低，体积应变由剪胀逐渐倾向于剪缩。颗粒破碎抑制了“剪胀”的发生，对试样的体积变化产生了较大影响，同时亦会降低峰值强度。

图5 颗粒破碎随剪切变形的演化规律（以平行键破坏率为颗粒破碎表征）Fig.5 Evolution of particle breakage with shear deformation(characterization of crushable by parallel bond broken rate)

剪切过程中颗粒破碎的位置与剪切带的位置密切相关，如图6所示。可以看出，随着轴向应变的增加，颗粒破碎的位置逐渐集中，试样达到临界状态后逐渐出现局部的颗粒破碎带，并与剪切带位置一致。并且随着破碎率的升高，颗粒总体破碎程度增大，颗粒破碎带的分布也更宽更广，使得颗粒破碎带（剪切带）集中性减小。更加印证了颗粒破碎使得变形增加，颗粒破碎集中在变形集中的剪切带，颗粒破碎的增加（从低破碎率到高破碎率），使得土样压缩变形增加，体积趋于减小，宏观应力应变响应也从密砂响应趋向于松砂响应。

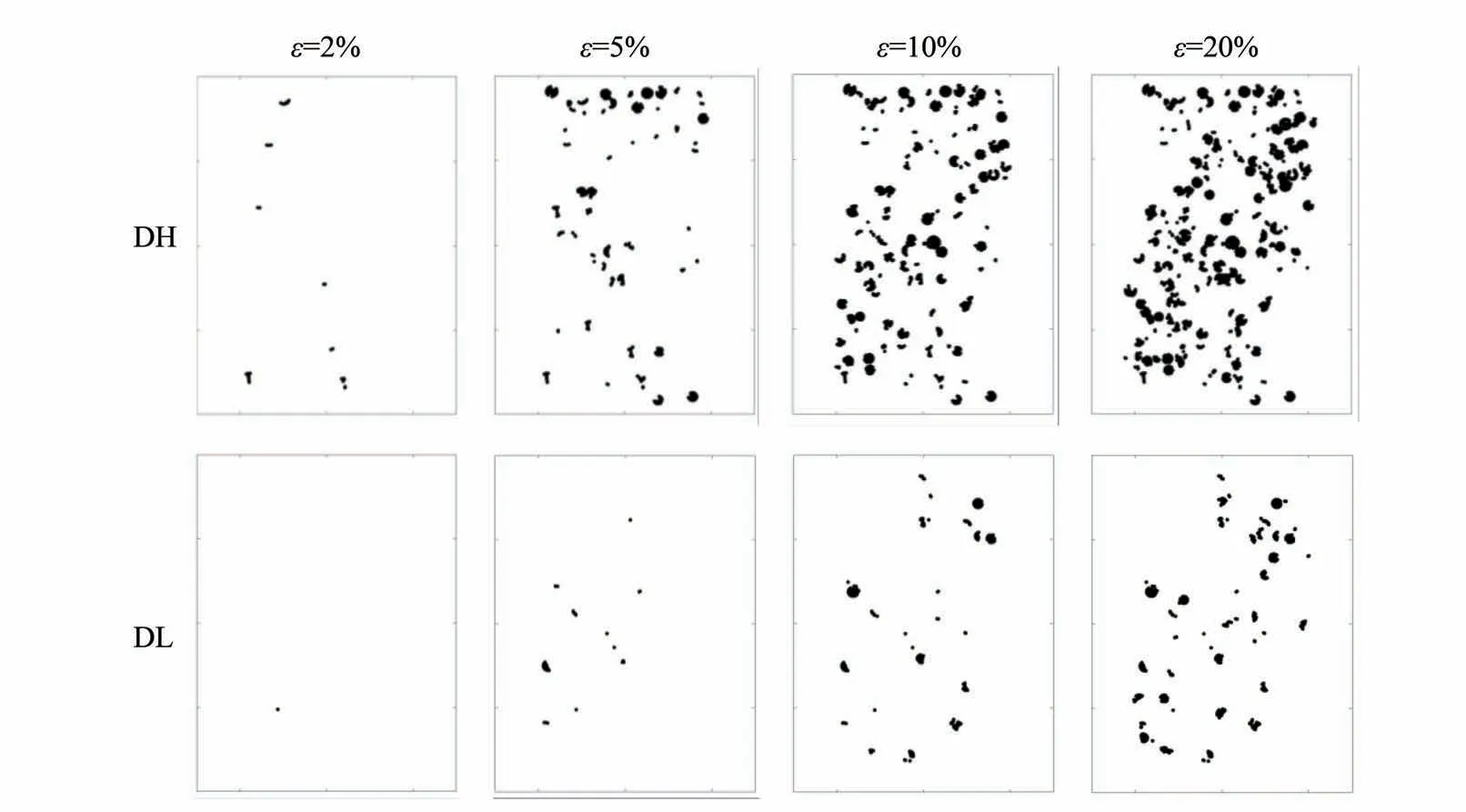
图6 不同颗粒破碎率的颗粒破碎位置分布图Fig.6 Distribution of particle breakage locations for different crushing rates

3.2 能量演化

下面主要分析钙质砂剪切过程中的能量演化。由于采用伺服机制保持围压，整个剪切过程都是准静态加载，动能较小相较于其他能量可忽略不计。图7是两种破碎率的密砂不同能量分量关于轴应变变化曲线。由于剪切加载方式为应变控制式，整个剪切过程中边界功的输入变化都非常均匀，且2个试样总输入功基本一致。剪切初始能量以Es的形式储存在颗粒接触中。随着剪切的进行，后期的输入功主要由颗粒间的摩擦耗散，Ef在整个剪切过程中起主要作用。对于高、低破碎率钙质砂剪切过程中的能量分配，可见，DH 钙质砂的破碎能量明显高于DL钙质砂，Ep的增加使得Es减小与Ed增大。整个过程能量始终守恒。

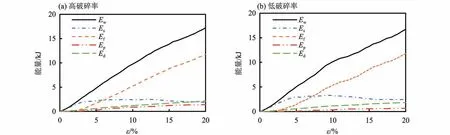
图7 试样能量累积曲线Fig.7 Energy accumulation curve

图8为相同能量分量在不同破碎率试样剪切过程中对比曲线，更直观地对比不同破碎率钙质砂在剪切过程中能量耗散项演化的差异。两个试样Ef总耗散值基本一致（图8（a）），能量值的差异主要体现在Es、Ep与Ed等3 个分量上。颗粒破碎影响了应变的积累，因此DH 试样Es积累峰值会低于DL（图8（b）），其值的降低也与应变硬化相对应。而尽管DH 试样的Ep值大于DL 试样（图8（c）），但对比其最终破碎率的比值（DH 破碎率为DL 的5.15倍），其Ep最终值的比值为2.11，说明随着破碎率的降低，单颗粒强度的增加，颗粒破碎本身所耗散的能量也会随之增大，使得低破碎率下Ep的降低与破碎率降低的值不一致。此外由于颗粒破碎瞬间会使得动能波动，DH 试样Ed值亦会大于DL试样（图8（d））。

图8 不同破碎率能量累计值对比曲线Fig.8 Comparison between the cumulative energy value of samples with different crushing rates

增量能量比能够更直观表征剪切过程中不同阶段的能量输入/耗散变化行为。增量能量比为增量能量分量输入/耗散项，即dEf/dEw、dEs/dEw、dEp/dEw和 dEd/dEw。在剪切的任何阶段，能量遵循输入与输出守恒，即

可转化为

图9 为不同破碎率的4 个主要的能量组成的增量与外界功增量的比值随轴向应变增加的演化过程。从整体看，4 个分量能量增量比的总和在任何时刻≈1，满足能量守恒。摩擦耗能增量比dEf/dEw与应变能增量比dEs/dEw的主要变化均发生在5%的轴向应变（峰值应力）之前。随着剪切进行dEf/dEw逐渐增加，dEs/dEw逐渐减小。当试样达到临界阶段后，这两部分能量增量也基本达到稳定状态。与之相反，破碎耗能增量dEp/dEw与阻尼耗能dEd/dEw在达到峰值应力前变化十分稳定，到达临界状态后则开始发生波动，表明显著的颗粒破碎从峰值应力开始，与图5颗粒破碎率结果一致。

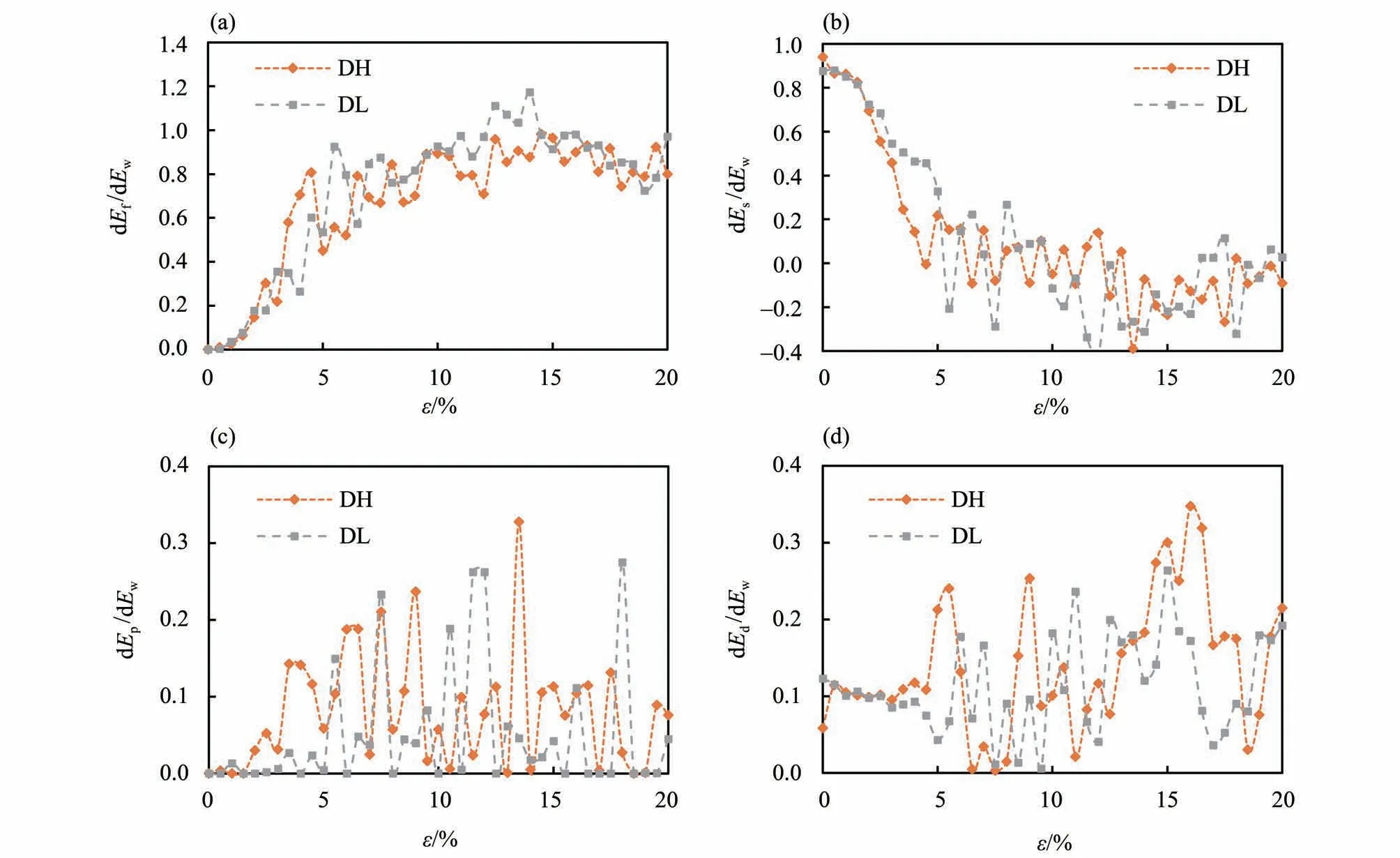
图9 各部分增量能量比与轴向应变的关系Fig.9 Relationship of the incremental energy components vs.axial strain

在剪切初始，dEs/dEw≈0.9，dEf/dEw≈0（图9（a，b））。这是因为剪切初期应力较小，密砂试样处在压密阶段，颗粒还未开始发生破碎，由于颗粒接触处的弹性压缩，输入功起始主要转变为Es储存在颗粒接触中，初始dEp/dEw≈0（图9（c））。dEd/dEw占比约0.1（图9（d）），这是因为为避免阻尼耗能过大掩盖摩擦耗散所起到的作用，局部阻尼系数设置了一个较低的值（0.1）。

随着剪切的进行，dEs/dEw随轴向应变的发展迅速减小，ε达到5%（即峰值应力）之后，数值维持在0 附近摆动，Es积累达到峰值，由于DH 试样颗粒强度更低，故其Es积累更快达到极限值。在后期DL 试样dEs/dEw的降低趋势比DH 试样明显，其原因为颗粒破碎阻止了DH试样Es的积累，同时也提供了大量细颗粒填充到孔隙中，使得颗粒接触更加紧密，试样压缩变形增加，中和了Es的减少值，而DL 试样形成了剪切带，整体发生破坏，带外颗粒Es积累达到饱和，而带内颗粒随着重排列部分应变能被释放，Es积累亦受到影响。dEf/dEw一直呈增长趋势，随着偏应力到峰值应力后，在0.8 附近上下波动，与dEs/dEw变化情况相对应的是DH 试样dEf/dEw增加的速度更快，可见，剪切过程中系统做功大多通过摩擦耗散。dEp/dEw与dEd/dEw在剪切前期保持稳定状态，当试样达到临界状态后，颗粒破碎迅速增加，这两部分增量比开始波动，这是由于颗粒发生破碎后，黏结键破裂，破碎本身耗散一部分能量外，阻尼器会吸收一部分破碎瞬间所释放的弹性应变能，并且子颗粒“自由”瞬间会产生颗粒间相对滑动导致dEf/dEw随之增加。由于颗粒破碎率越高，颗粒破碎程度越大，因此，DH 试样的dEp/dEw波动更大，其占比也会大于DL试样。

对比发现，不同破碎率Ef总积累值基本一致（图8（a）），但事实上两个试样的颗粒破碎程度有较大差别，而颗粒破碎显然会影响内部能量的分配。在剪切过程中，试样Es的积累与颗粒破碎的竞争会影响其宏观的应力应变与体积变化行为，两者都促进了摩擦与阻尼耗散。颗粒破碎通过产生更多细颗粒，在大应变状态下促进输入功的耗散。另外，试样到达临界条件后发生剪胀，颗粒间的重排列亦能促进能量耗散。故虽然两个试样Ef总值没有差别，但其机理却并不一致，DH 试样内Ef的增加主要是由颗粒破碎后子颗粒产生的摩擦耗散提供；DL 试样中摩擦能的增加更多是剪切带内颗粒重排提供。

图10～12 为钙质砂剪切过程中累积的Ef、Es与Ep的分布演化图。由图10 可知，Ef在整个剪切过程中持续积累，其分布与剪切带的分布具有强相关性，随着剪切的进行，密砂Ef逐渐集中在剪切带内。Es在轴应变达到5%时就基本上完成了积累，后期基本不再发生大的变化。DH 试样Es分布比较均匀，自始至终没有表现出明显集中的规律性，而DL 试样剪切带内由于颗粒运动，部分Es被释放。Ep分布与剪切带分布也有强相关性，DH 试样Ep发展的变化同Ef分布变化一致，但是DL试样Ep与Ef分布尽管都集中在剪切带内，但是其摩擦耗散较集中破碎耗散较分散，说明Ef主要依靠剪切带内颗粒相对运动提供。这也再次佐证：对于DH 试样内部能量耗散的机制是主要依靠颗粒破碎来完成，而DL 在剪切过程中能量的耗散则更多得依靠试样整体的错动（即颗粒重排）实现。

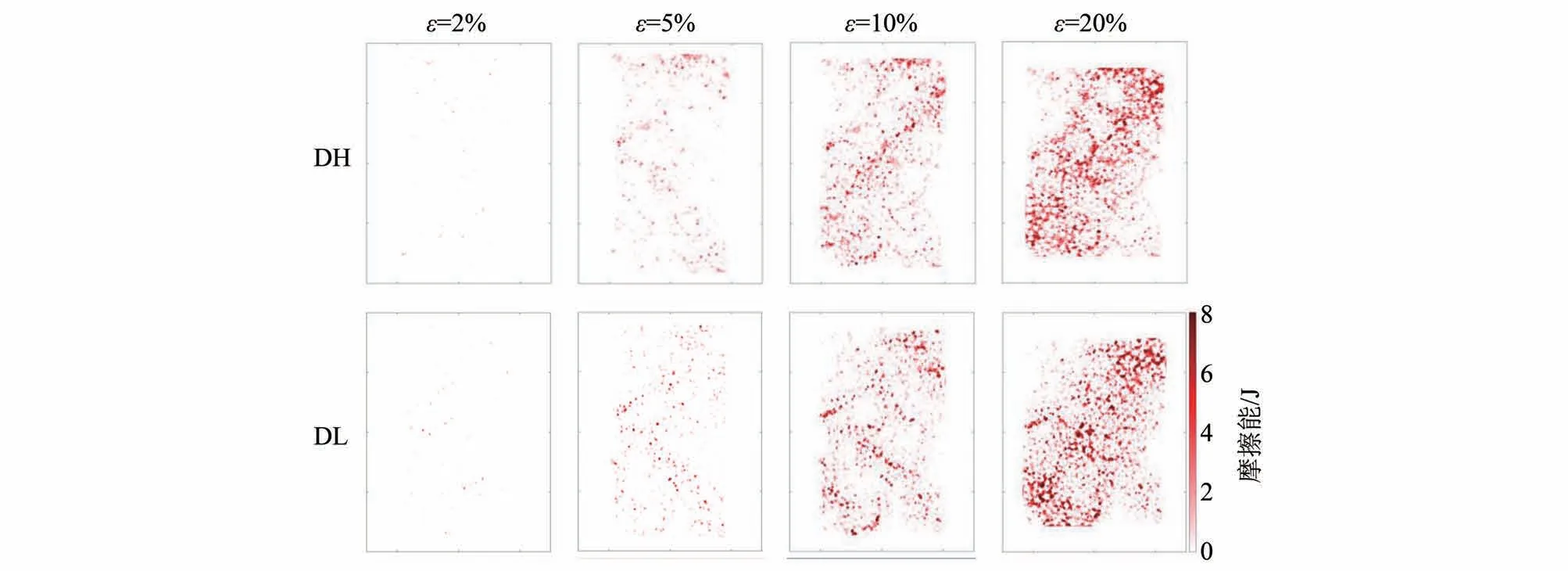
图10 摩擦能分布图Fig.10 Distribution of frictional energy

图11 应变能分布图Fig.11 Distribution of strain energy

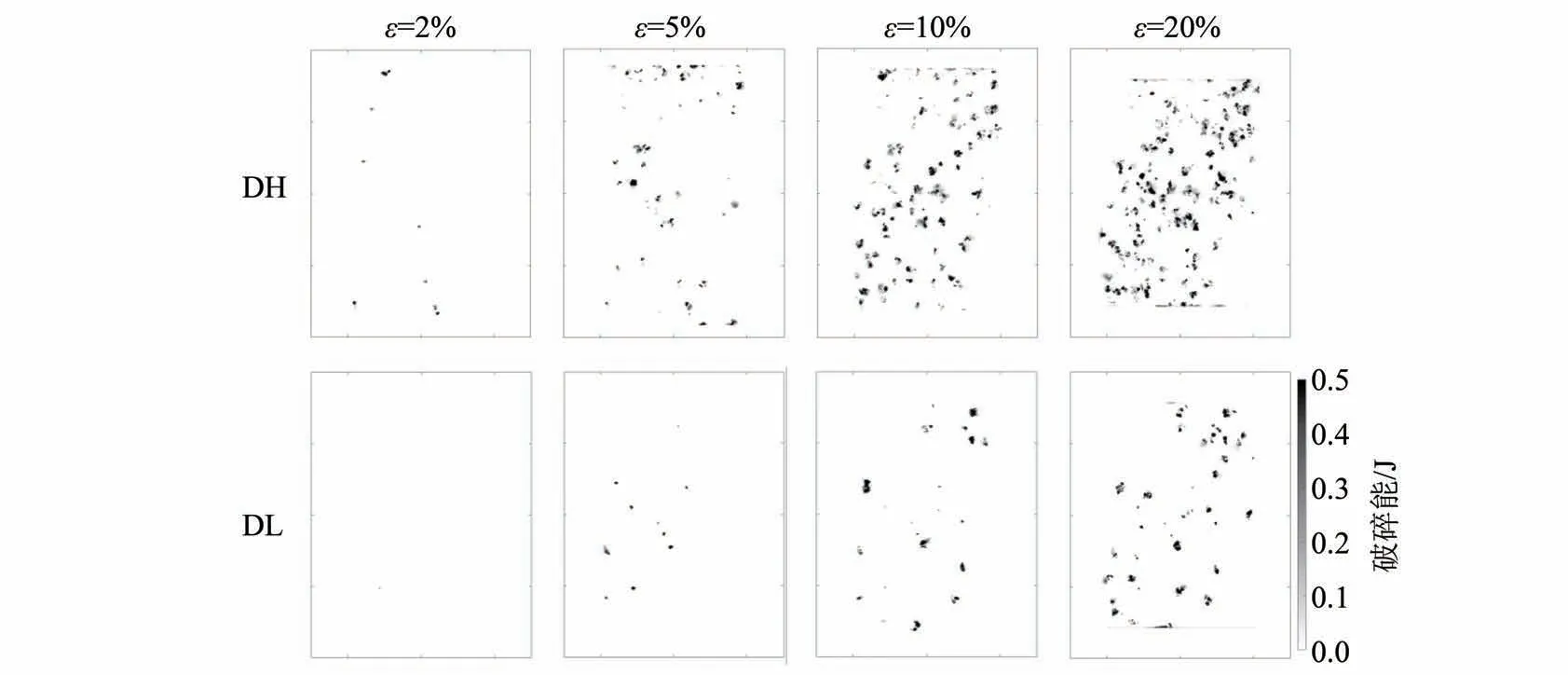
图12 破碎能分布图Fig.12 Distribution of breakage energy

综上可知，剪切过程中的能量耗散由摩擦能、应变能、破碎能与阻尼能组成，其中，摩擦能起主要作用，其次是破碎能与阻尼能，应变能最小。摩擦能与颗粒间相对运动密切相关，破碎能和应变能跟颗粒破碎密切相关。密砂的摩擦能集中在剪切带内，宏观剪胀明显。但剪切过程中的颗粒破碎增加了破碎能的占比，降低了应变能，削弱了原有颗粒的相对运动，使得应变集中减弱，使得宏观变形的剪胀作用减小。从能量角度阐释了宏观应力应变的响应，即，随着颗粒破碎程度增加，破碎能量增加，颗粒的应变能减小，使得颗粒内能减小，从而影响宏观变形由剪胀变为剪缩，应力由应变软化变为应变硬化，使得密砂的剪切响应转变为类似松砂的剪切响应（图4）。

4 结 论

本文运用离散元数值模拟方法研究了钙质砂在剪切过程中的能量耗散行为，揭示了颗粒破碎、颗粒强度以及微观能量耗散对钙质砂宏观力学性质的影响机理。得出如下结论：

1） 钙质砂试样在剪切过程中应力应变关系以及体积响应表现出密砂的典型特征，随着钙质砂颗粒破碎率的增大，其宏观应力应变关系逐渐由应变软化向应变硬化转变，同时伴随着剪胀性降低。颗粒破碎能够促进钙质砂的压缩变形，同时影响峰值强度。

2） 颗粒破碎在整个剪切过程中持续发生，在临界状态下钙质砂颗粒需要更大的能量输入才能继续发生破碎，颗粒破碎带与剪切带具有强相关性，颗粒破碎位置逐渐集中于剪切带内，而破碎率的增加会分散颗粒破碎带的集中性。

3） 摩擦耗能与颗粒间相对运动密切相关，在整个剪切过程中起主要作用，破碎能和应变能跟颗粒破碎密切相关，颗粒破碎减少了应变的积累，使得应变能峰值降低，而其破碎本身就会引起能量耗散。随着单颗粒强度的增加，破碎耗散的能量增大，因此破碎耗能的降低的幅度与破碎率降低的幅度不一致。

4） 不同破碎率钙质砂在剪切过程中能量耗散的特征有所不同。低破碎率在剪切过程中能量主要通过剪切带内的摩擦以及带内颗粒应变能释放耗散。高破碎率的颗粒破碎使得摩擦耗散的集中性被降低，但中和了应变能的降低，使得钙质砂试样整体更均匀，宏观上即表现为密砂的剪切响应转变为类似松砂的剪切响应。