颗粒摩擦对散粒堆积体拱效应的影响*

戴北冰， 邓林杰， 陈智刚

1.中山大学土木工程学院，广东 珠海 519082

2.南方海洋科学与工程广东省实验室（珠海），广东 珠海 519082

3.重庆建工第一市政工程有限责任公司，重庆 400020

散粒材料在自然界和人类生产生活中普遍存在（Terzaghi，1936；Karl，1943）。散体颗粒在重力或其他外力因素作用下形成的堆状颗粒集合体称为散粒堆积体（Nedderman，1992；贾海莉等，2003）。散粒堆积体的自然休止角以及内部的拱效应是其重要的物理力学特征，在农业、工业、制药等领域有着十分重要的应用背景和研究价值（Dai et al.，2017； Dai，2018）。

散粒堆积体内应力的分布一直是学者们感兴趣的研究对象（戴北冰等，2022；Dai et al.，2022）。学者们在沙堆中观察到了一种有趣且违反直觉的现象，即沙堆锥顶正下方的底部垂直应力会出现局部最小值，即堆积体底部形成“M”形应力分布（Wittmer et al.，1996；Watson，1996；Cates et al.，1999），这种现象称作应力凹陷现象。应力凹陷与拱效应紧密相关，堆积体内部的应力拱使应力传递产生了屏蔽效应，导致应力分布局部化和不均匀化，从而引起沙堆顶部正下方底部应力的局部下降（Fang et al.，2022）。因此，研究应力凹陷现象对理解沙堆中的拱效应至关重要。众多学者已围绕颗粒形状（Zuriguel et al.，2007；Zuriguel et al.，2008；Zhao et al.，2019）、颗粒摩擦（Geng et al.，2001；Silbert et al.，2002；Goldenberg et al.，2005；Horabik et al.，2017）等影响因素，对应力凹陷现象开展了较为深入的研究，发现：随着颗粒摩擦的增大，沙堆底部压力局部下降越明显，应力凹陷现象增强。Fang et al.（2022）发现，不同颗粒粒径形成的沙堆内摩擦角不一致，内摩擦角大的沙堆底部应力凹陷越明显，这也间接佐证了颗粒粒径会影响沙堆的应力凹陷。Goldenberg et al.（2005）和Zhou et al.（2009）通过数值模拟发现：颗粒圆度越低，沙堆底部压力局部下降越明显。因此，颗粒基本性质对散粒堆积体底部的应力凹陷现象起着举足轻重的作用。

底部应力凹陷和拱效应的产生本质上是由力链的发展和传递实现的（Meng et al.，2018；Zaidi，2020），而颗粒摩擦是其重要的影响因素之一。许多学者研究了颗粒摩擦对力链传递的影响规律，发现散粒堆积体内强弱力链的相对位置和数量会随着颗粒摩擦的改变而改变（孙其诚等，2008；张炜等，2022），堆积体内强力链传递了大部分荷载（Ma et al.，2016；戴 北 冰 等，2019）。张 炜 等（2022）在研究铁粉末压制过程中力链演化规律时，发现随着颗粒间摩擦系数增大，整体力链数目变少，力链方向系数变大。Zhu et al.（2013）发现，对于较大的颗粒摩擦，强力链倾向于在更陡的方位上分布，形成更稳定的拱形以承担更多的沙堆重量。Bouchaud et al.（2002）通过光弹实验分析了颗粒集合体在外力作用下的排列和相互作用，以及力链的传递路径。Majmudar et al.（2005）测量了光弹颗粒集合在纯剪切和各向同性压缩作用下法向力和切向力的传递路径。由此可见，颗粒摩擦对散粒体堆积体中的力链传递以及拱效应的发挥机制有着显著影响。

目前，学者们虽然在关于颗粒摩擦对土拱效应影响方面做了许多工作，但尚未深刻阐明颗粒摩擦对散粒堆积体内部细观力学响应的影响规律以及不同颗粒摩擦影响下拱效应产生的细观力学机制。本研究旨在利用DEM 模拟，研究颗粒摩擦对散粒堆积体宏细观力学行为的影响，通过将堆积体内部大于平均接触力的接触力沿锥角方向进行投影、统计颗粒接触方位的概率密度分布来分析散粒堆积体内部拱效应的优势发挥方位，基于统计分析研究堆积体内部强弱力链占比，对不同颗粒摩擦下散粒堆积体内力链网络进行可视化分析，建立宏观力学特征与细观力学指标的联系，以揭示散粒堆积体内拱效应形成的细观力学机制。

1 颗粒设计以及堆积体建模

本文使用DEM 程序PFC3D 来模拟沙堆的形成，数值模拟所用的材料是一种理想的弹性颗粒材料，如图1 所示。颗粒形状系数Ra（即子颗粒的直径与颗粒的长度之比）为0.6，颗粒粒径（与该颗粒体积相等的球体直径）在0.01～0.015 m 之间分布，相关模型参数如表1所示（戴北冰等，2019）。数值模拟采用了8 种不同的颗粒摩擦系数(μ= 0.01，0.05，0.10，0.30，0.50，0.70，1.00、2.00)，以研究颗粒摩擦对散粒堆积体拱效应的影响。所有模拟中，重力加速度均采用10 m/s2，底部墙体的摩擦系数为0.50。数值模拟中颗粒粒径保持一致，不会影响所发现的颗粒摩擦影响规律。

表1 离散元数值模拟参数Table 1 Discrete element numerical simulation parameters

图1 颗粒形状Fig.1 Particle shape

本数值模拟通过点源释放法来形成散粒堆积体，颗粒释放工具如图2所示。释放器上方豁口是边长为0.25 m的正方形，释放器下方豁口是边长为0.075 m 的正方形，释放器高度为2.5 m，组成释放器的所有墙体的摩擦系数均为0。在本数值模拟中，散粒堆积体内一共有约2×104个颗粒，由释放器分10次下落形成，每次下落都保证释放器底部离堆积体最高处（第一次为水平面）为一固定高度0.5 m。

图2 漏斗型释放器Fig.2 Funnel type releaser

2 分析与讨论

2.1 堆积体休止角计算及分析

图3给出了不同颗粒摩擦条件下所形成的堆积体数值模型。可以看出，μ为0.01 和0.05 时，难以形成具有明显坡角的堆积体；μ为0.10～0.50时，可以观察到形成的堆积体有明显的坡角，且坡角随着μ的增大而增大；μ超过0.50后，坡角基本不变。图4给出了自然休止角α与颗粒摩擦系数μ的关系。从图3 和图4 可以发现，在颗粒间摩擦系数μ小于0.50 时，自然休止角α随着颗粒摩擦系数的增加而增加，在颗粒间摩擦系数μ> 0.50后，自然休止角α趋于一个稳定值。

图3 不同摩擦系数形成的散粒堆积体Fig.3 Granular heaps on different inter-particle friction

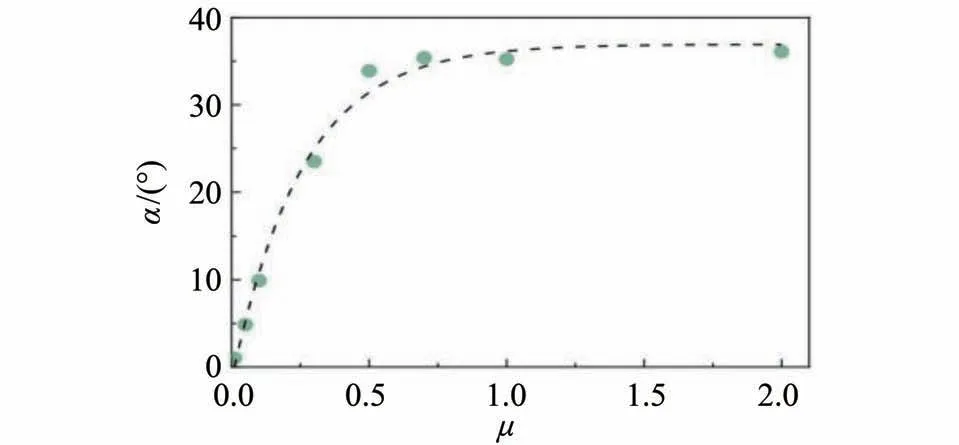
图4 不同颗粒摩擦系数下堆积体的自然休止角Fig.4 α of granular heaps with different inter-particle friction

2.2 颗粒堆积体底部接触力分析

图5给出了不同摩擦条件下堆积体底部接触力的云图，X、Y坐标的单位为m，色卡的数值单位为N。可以发现，μ为0.01 时，堆积体底部接触力的峰值出现在中心位置；μ为0.05～2.00时，堆积体底部接触力的峰值不在中心位置，而是出现在偏离中心的位置。进一步观察可以发现，随着颗粒摩擦系数增大，堆积体底部中心区域的颜色由红色（μ= 0.01）变 为 黄 色（μ= 0.05），然 后 是 绿 色（μ≥0.10），最后是蓝色（μ≥0.70）。红色代表应力水平相对较高，而蓝色代表应力水平相对较低。因此，从中心区域颜色的变化趋势可以判断中心区域应力水平相比较于整个底部区域应力峰值水平的差距。随着摩擦系数的增大差距增大，并在μ> 0.5 后，这种差距几乎趋于稳定，意即底部应力凹陷现象随着摩擦系数增加而变得显著，并逐步趋于稳定。

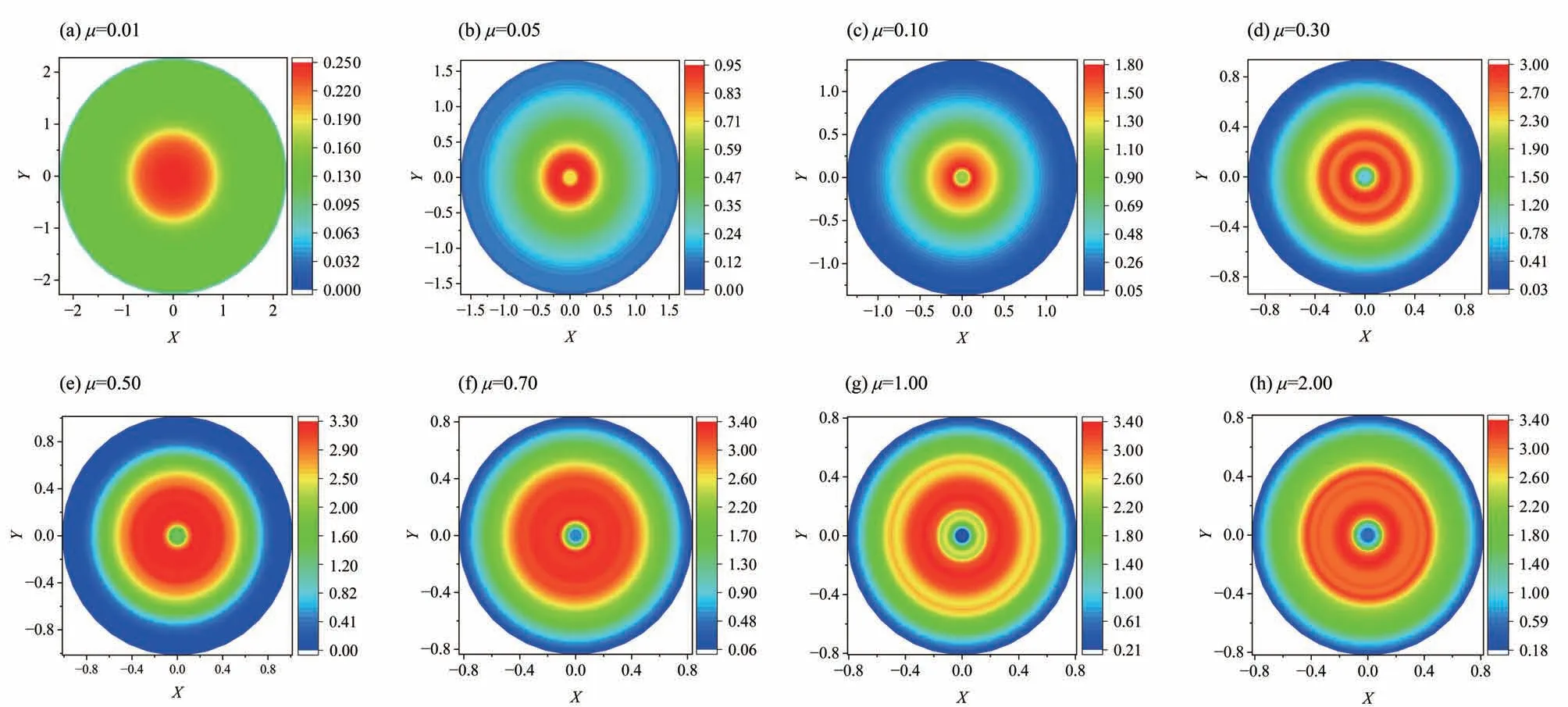
图5 堆积体底部接触力云图Fig.5 Cloud chart of contact force at the bottom of granular heaps

图6为堆积体底部法向接触力和切向接触力沿半径方向的分布，x/R是参考位置到圆心距离与堆积体底部圆半径的比值。可以发现，颗粒摩擦系数μ= 0.01时，底部法向和切向接触力分布均未出现应力凹陷现象。当μ= 0.05时，底部法向和切向接触力分布则出现了微弱的应力凹陷现象。随着μ继续增大，堆积体底部法向和切向接触力的峰值明显地增大，并在μ> 0.50后变化不大，而堆积体底部中心处法向和切向接触力的峰值则表现出先增大（μ< 0.5）后减小（μ> 0.5）的趋势。

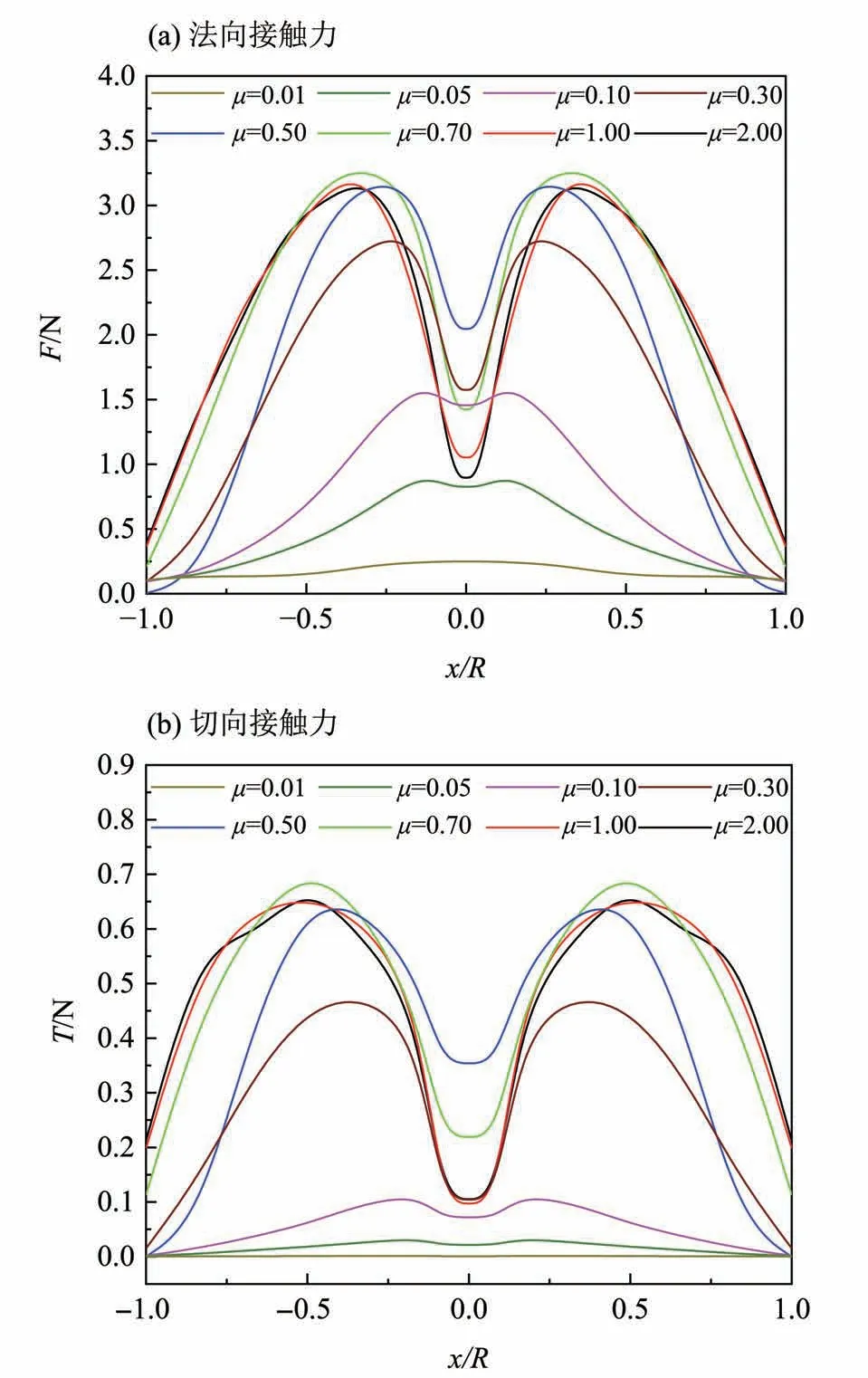
图6 底部法向和切向接触力沿半径方向的分布Fig.6 Distribution of normal contact force and tangential contact force at the bottom along the radius

图7-8给出了堆积体底部峰值接触力、中心接触力以及中心接触力相对于峰值的减少程度随颗粒摩擦系数的变化。从图7可以发现，随着颗粒摩擦系数的增大，堆积体底部接触力峰值先增大，后逐渐趋于一个稳定值；堆积体底部中心处的接触力则先增大后减小。图8显示中心接触力的减小程度随着摩擦系数的增大而增大，亦有逐步趋于稳定的趋势，这进一步佐证了底部接触力云图的观察发现，即底部应力凹陷现象随着颗粒摩擦系数的增大而增强，并在颗粒摩擦较大的情况下趋于稳定。

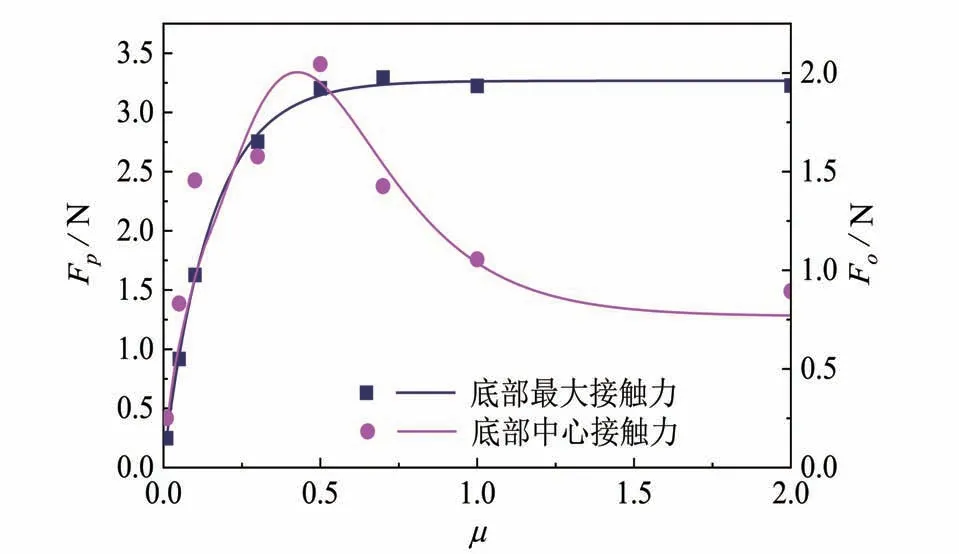
图7 峰值接触力与中心接触力随颗粒摩擦系数的变化Fig.7 The change of the peak contact force Fp and the center contact force Fo with inter-particle friction

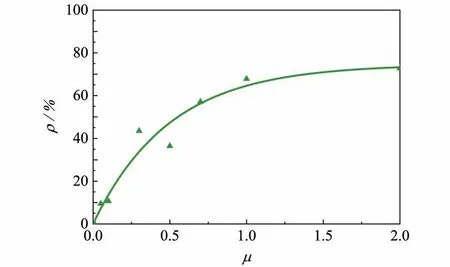
图8 中心接触力相对于峰值的减少程度Fig.8 The decreasing degree of the center contact force relative to the peak value

图9 给出了底部接触力峰值位置xp/R与μ的关系。可以发现，随着μ增大，峰值位置从底部中心逐渐往外迁移，并在μ> 0.50后，峰值位置维持在xp/R= 0.21左右。

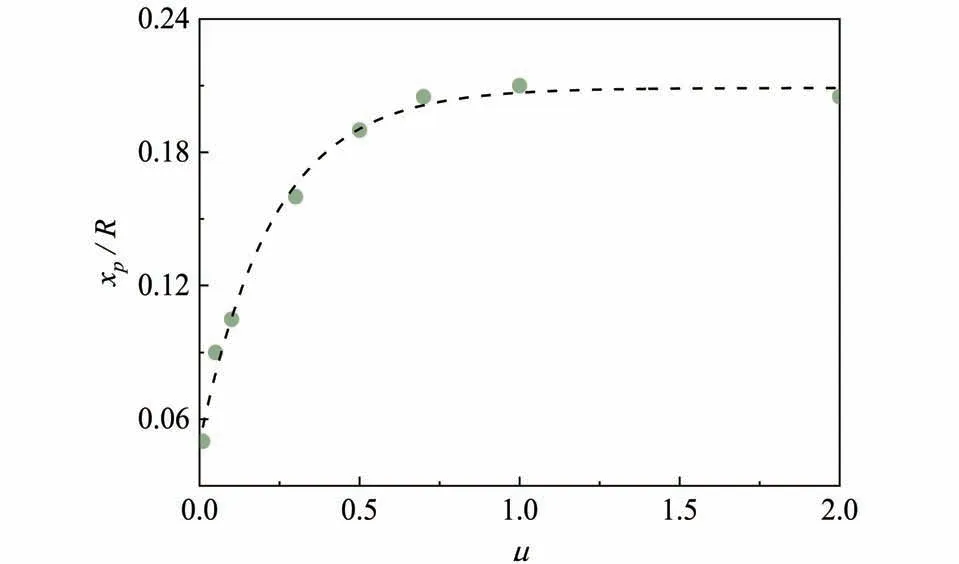
图9 底部接触力峰值位置与颗粒摩擦系数的关系Fig.9 The relationship between the position of the peak contact force at the bottom and the inter-particle friction coefficient

2.3 颗粒间接触力投影

散粒堆积体的形成与稳定取决于其内部颗粒间的相互作用，力链的传递对拱效应的形成起着关键作用。为进一步分析颗粒间接触力的传递对拱效应形成的影响以及拱效应的优势发挥方位，将堆积体内部大于平均接触力的接触力在如图10所示的a⇀、i⇀、m⇀（其中m→为沿锥角方向，i→为与m→垂直的环向方向，a→为与i→、m→垂直的方向）三个方向进行投影。

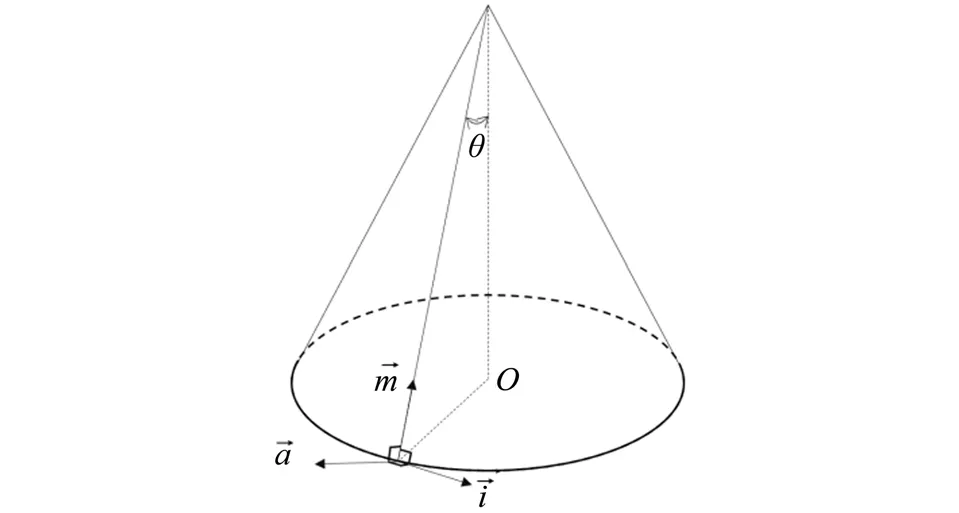
图10 投影方式示意图Fig.10 Schematic diagram of projection mode

图11-13 为法向接触力、切向接触力、总接触力沿a⇀、i⇀、m→三个方向的投影值，纵坐标F为接触力的投影值大小，横坐标为投影角度θ。

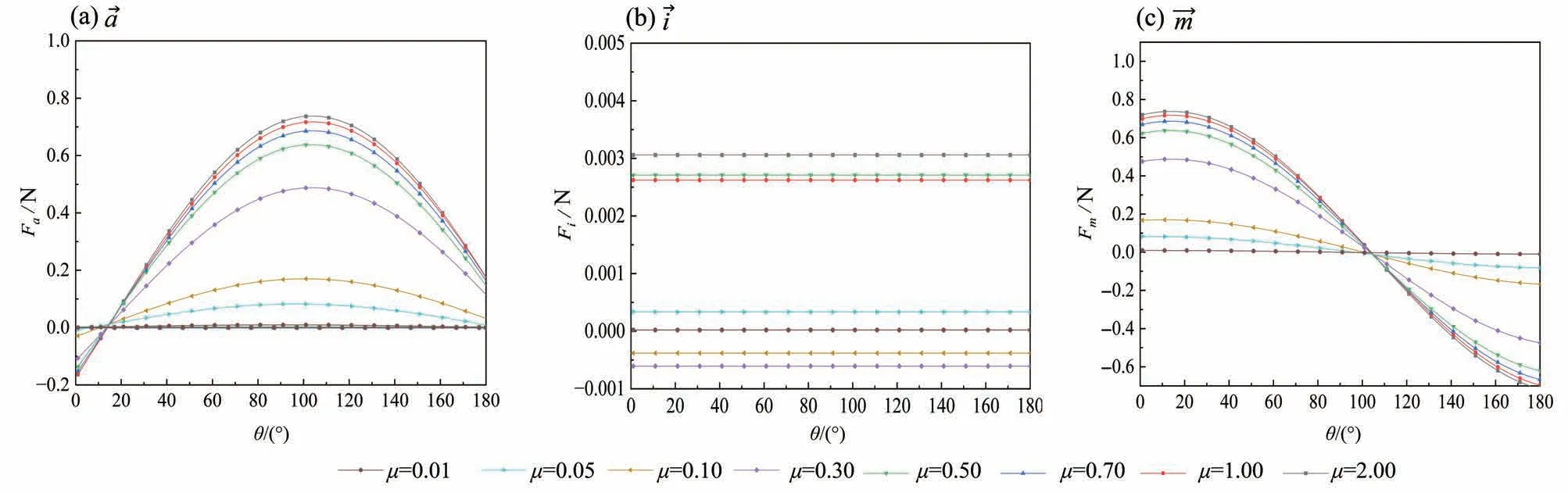
图11 法向接触力沿a→、i→、m→三个方向的投影值Fig.11 Projection value of normal contact force along a→、i→、m→

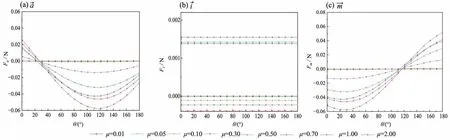
图12 切向接触力沿a→、i→、m→三个方向的投影值Fig.12 Projection value of tangential contact force along a→、i→、m→

从图11-13 可以发现，沙堆内部颗粒法向接触力和切向接触力在各个方向上的投影值大小随着颗粒间摩擦系数的增大而增大，且在i→方向（环向）的投影几乎为零，这也间接证明了应力在环向是对称的。法向接触力在a→方向的投影值在θ= 15°左右时为0，而在θ= 105°左右达到最大。显然，投影最大值和最小值的方位刚好差90°。由于m→与a→垂直，法向接触力在m→方向的投影规律与a→方向的相反，投影值在θ= 105°左右为零点，而在θ= 15°左右时达到最大，即沿着m→与a→投影峰值（或者零点）的方位刚好相差90°。切向接触力在a→方向的投影值在θ= 25°左右时为0，在θ=115°左右时达到最大，而在m→方向的投影值则在θ= 115°左右时为0，在θ= 25°左右时达到最大。如图13 所示，由于切向接触力较法向接触力小很多，因此总接触力的投影规律主要受法向接触力控制，与图11中法向接触力投影规律几乎相同。这里需注意的是，对于μ= 0.01 和0.05 的情况，法向接触力和切向接触力投影值均很小，这主要是因为颗粒在这两种摩擦状态下很难形成有效的堆积。

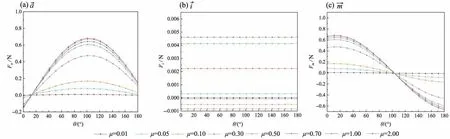
图13 总接触力沿a→、i→、m→三个方向的投影值Fig.13 Projection value of total contact force along a→、i→、m→

图14 给出了沿m→向（即锥面方向）投影值峰值所在的方位角度θ与摩擦系数的关系。可以看出，无论是法向接触力、切向接触力，还是总接触力，投影峰值方位角度θ随着μ的增大而增大，直至达到一个稳定值。如果不考虑摩擦系数较低的情况（μ≤0.1），法向接触力和总接触力的投影峰值方位接近θ= 15°，而切向接触力的投影峰值方位接近θ= 25°。

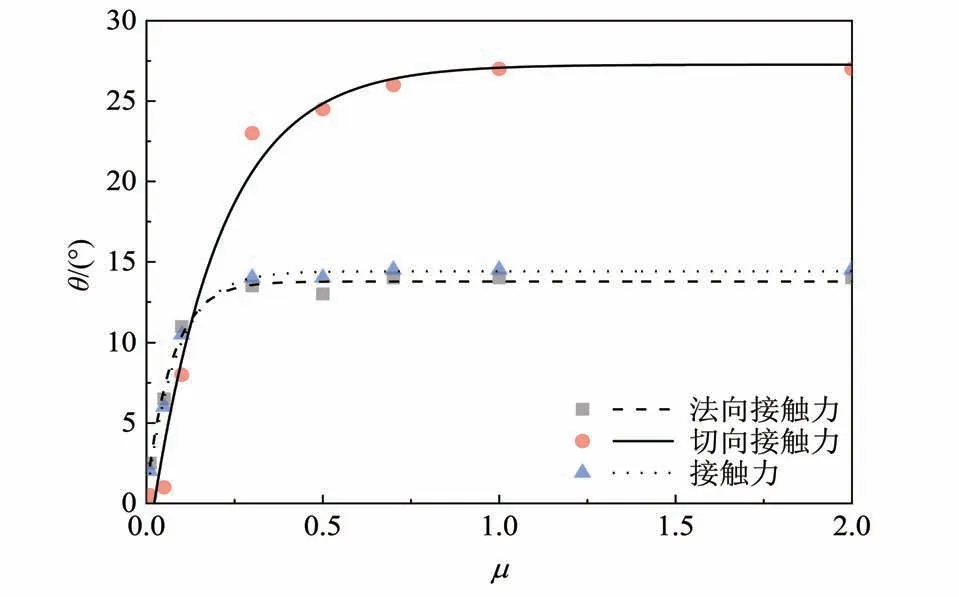
图14 法向接触力、切向接触力和总接触力沿m→向投影峰值所在的方位角Fig.14 The orientation angle when conical surface force,tangential contact force and total contact force reaches the peak value along m→

2.4 颗粒接触方位向量

图15为颗粒接触方位的概率密度f分布。由于散粒堆积体基本呈锥形，可以近似认为颗粒接触方位在环向是对称分布，因此这里只考虑颗粒接触以竖直轴作为参考基准的方位分布规律。γ为颗粒接触方位相对于竖直轴的方位角，取值范围为0°～90°。从图15可以看出，随着γ的增大，颗粒接触方位的概率密度f基本呈先增加后降低的趋势，但概率密度峰值fmax的方位γ因摩擦系数不同而不同。μ= 0.01 时，fmax出现在γ= 35～40°；μ= 0.05时，fmax出现在γ= 30～35°；μ= 0.10 时，fmax出现在γ= 20～30°；μ= 0.30～2.00 时，峰值出现在γ=15～25°的时候。可以看出，峰值方位角随着摩擦系数增大而降低，但当μ> 0.30时，峰值出现的方位（γ= 15～25°）不随颗粒摩擦系数的增加而显著改变，且该方位范围与法向接触力投影峰值的方位（θ≈15°）以 及 切 向 接 触 力 投 影 峰 值 的 方 位（θ≈25°）非常接近（见图14）。需指出的是，这里的θ方位亦以竖直轴为参考。这些观察充分证明了在颗粒摩擦系数较高（μ ≥0.3）的情况下，散粒堆积体内部拱效应的优势发挥方位出现在偏离竖直轴15°～25°的方位。

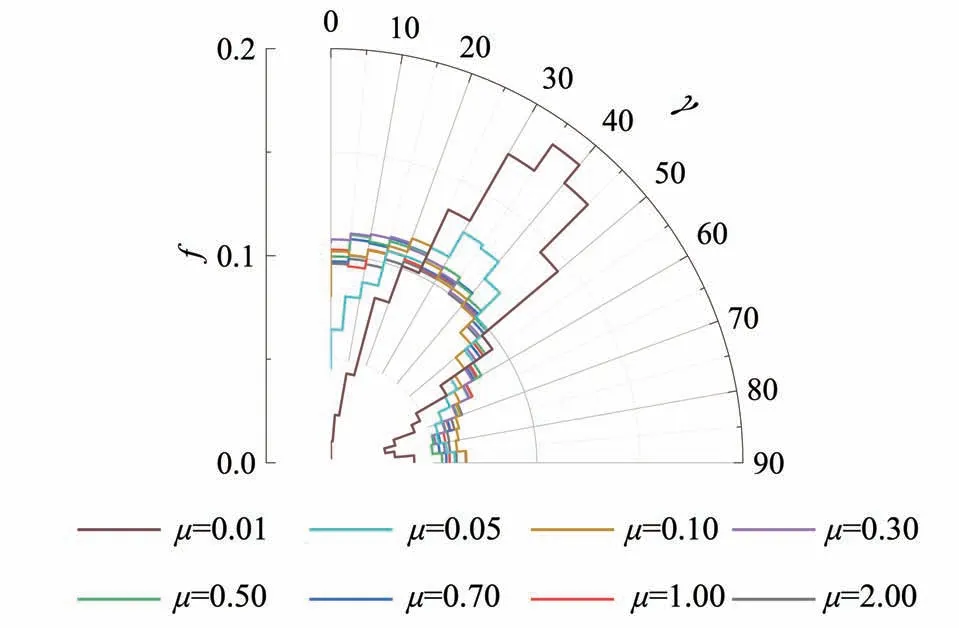
图15 颗粒接触方位概率密度分布Fig.15 Probability density distribution of particle contact orientation

2.5 堆积体中力链统计

图16 统计了堆积体中弱力链的出现概率。弱力链是指接触力小于平均接触力的力链。Pn是指法向接触力弱力链的概率，Pt是指切向接触力弱力链的概率。由图16 可知，Pn随着颗粒摩擦系数的增加而微弱增加，并在μ大于0.10后，维持在0.68 左右。Pt在摩擦系数较低时接近1.0，而在μ大于0.30 后，随着μ的增加而降低。可以发现，不论是法向接触力还是切向接触力，堆积体内弱力链的数量总是多于强力链的数量；切向接触力中弱力链的占比要高于法向接触力中弱力链的占比；随着摩擦系数的增大，部分切向接触力的弱力链会逐渐转化为强力链。

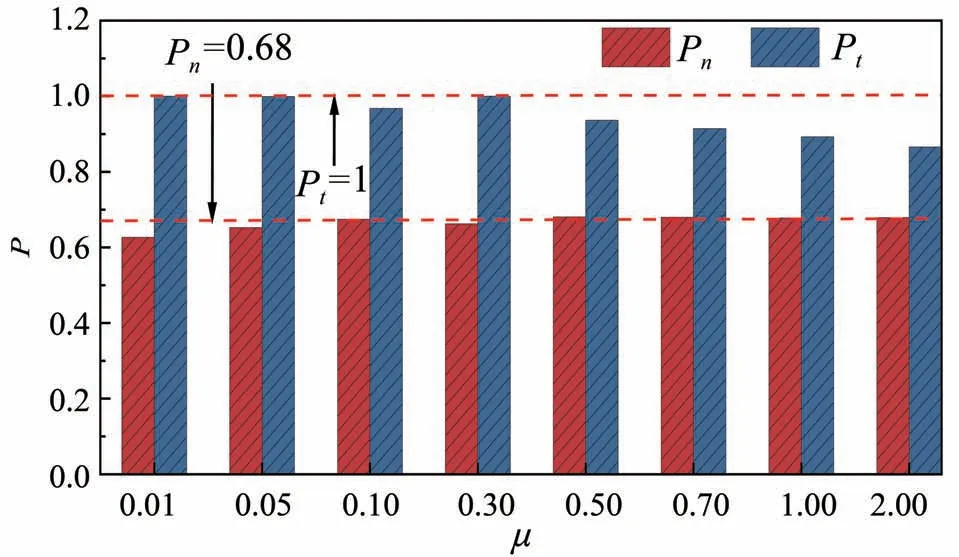
图16 弱力链统计Fig.16 The statistics of weak force chains

图17 给 出 了μ= 0.05，0.10，0.30，0.50 时 堆 积体的力链网络图。图中力链粗细（或颜色）表征接触力的大小。可以发现，平均接触力随着μ增加而增大。当μ= 0.05，0.10 时，散粒堆积体中的强力链数量偏少，且呈水平摊开的分布，难以观察到成“拱”现象。从图17 中可见，当μ ≥0.3 时，随颗粒摩擦系数的增大，强力链在水平和高度方向上逐渐扩展，强力链也逐渐与堆积体中心轴呈一定倾斜角度，成“拱”效应也越来显著。

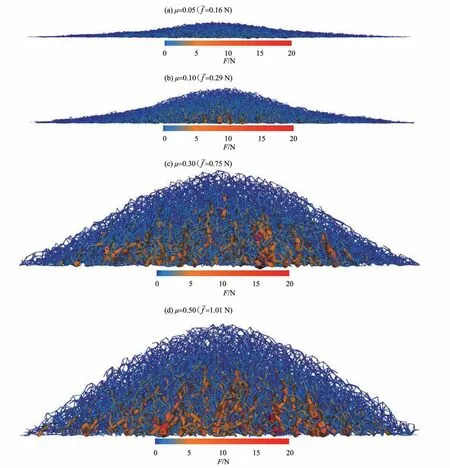
图17 散粒堆积体力链网络图Fig.17 Force chains network diagram of granular heaps

3 结 论

1）颗粒摩擦会影响堆积体休止角；摩擦系数越大，休止角越大；当颗粒摩擦系数大于0.50 后，堆积体的休止角趋于一个稳定值。

2）随着颗粒摩擦系数增大，堆积体底部中心接触力呈先增大后减小的趋势；底部接触力峰值先增大后趋于一个稳定值，其位置从底部中心xp/R= 0 逐渐往外迁移，最终维持在xp/R= 0.21 左右；底部中心处接触力值相对于峰值的减小程度ρ从0%增加到72.7%，堆积体底部应力凹陷现象增强。

3）在μ≥0.30 时，法向接触力和总接触力在m→向的投影峰值方位接近θ= 15°，切向接触力的投影峰值方位接近θ= 25°，且与接触方位向量的概率密度峰值方位接近，证明散粒堆积体内部拱效应的优势发挥方位出现在偏离竖直轴15°～25°的方位上。

4）在摩擦系数较低时（μ≤0.10），强力链的数量偏少且呈水平摊开分布，难以形成明显的拱效应；当摩擦系数较高时（μ≥0.30），强力链在竖直和水平方向扩展，并形成倾斜传递，促进拱效应的产生。