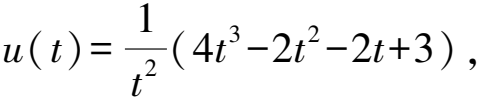2023年全国高考数学甲卷理科导数题解法探究

蒋依格 马绍文

(云南师范大学,云南 昆明 650504)

高考导数含参问题压轴题是一个经典的问题,文章具体阐述应用不同思想方法来解答2023年全国高考数学甲卷理科导数压轴题,旨在为高中数学一线教师提供教学参考.

1 试题呈现

(1)当a=8时,讨论f(x)的单调性;

(2)若f(x)

2 试题解析

2.1 第(1)问解法探索

分析第(1)问是求函数的单调性.解决此类问题一般利用导数求单调区间,或者利用换元简化计算再求单调区间.

对f(x)求导并化简,得

令f′(x)>0,则2cos2x-1>0.

令f′(x)<0,则2cos2x-1<0.

解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这种方法就是换元法.换元法在导数中有很好的运用,很多复杂的导数问题需要用到换元法[1].

对f(x)求导并化简,得

又因为sin2x=1-cos2x,

2.2 第(2)问解法探索

分析第(2)问主要考查含参不等式恒成立时参数的取值范围.解决此类问题本质就是解含参不等式,而解不等式通常是先研究对应的方程的根,因此围绕f′(x)根的分布,结合函数图象自然就产生了分类讨论的标准.讨论时要注意分类需不重不漏,对参数的所有可能取值都要讨论到,对应结论相同时参数范围要合并.整个解题过程充分体现了分类与整合数学思想方法的应用,也体现了函数与方程、化归与转化及数形结合的思想方法在解题中的应用.

令cos2x=t,t∈(0,1),化简得,

又因为t∈(0,1),所以只需判断分子的正负.

令c(t)=2t3+t-3,求导得

c′(t)=6t2+1>0.

则c(t)在(0,1)上单调递增,c(t)min=c(0)=-3;c(t)max=c(1)=0,c(t)∈(-3,0),c(t)<0.

则u′(t)<0,可得u(t)在(0,1)上单调递减.

因为u(1)=3,所以u(t)>u(1)=3.

所以f(x)>sin2x(0

综上,若f(x)

点评移项构造函数是一个常规方法,本题中对构造的函数h(x)=f(x)-sin2x求导判断其单调性,在求导的过程中较为繁琐,需要不断构造新的函数,最后结合函数图象进行分类讨论,在讨论中采用反证法排除a>3的情况,即可得到a的取值范围为a≤3.

对F(x)求导,得

得F′(0)=a-3<0,解得a<3.

现判断a=3时,f(x)

令cos2x=t,t∈(0,1),得

故a=3时,f(x)

综上,若f(x)

函数是整个高中数学的一条主线,导数是研究函数的有力工具,“函数与导数”又是高考数学的重要内容之一,故笔者立足于2023年全国高考数学甲卷理科导数压轴题,研究其解题方法,希望给予师生启发.数学考试的特点体现了数学研究对象的特点,而高考数学试题具有概念性强、充满思辨、量化突出、解法多样等显著特点.“解法多样”就是通常说的一题多解,它有利于考生发挥各自的特点,灵活解答,真正显现水平.因此,教师在教学过程中应帮助学生从不同角度进行观察和分析,引导学生抓住条件和结论之间的联系,进而开拓学生的解题思路,激发其解题兴趣,提升其发散思维能力.