例谈微元法在高中物理解题中的应用

解晓兵

(利辛县第二完全中学,安徽 利辛 236700)

在高中物理的解题过程中运用微元法是极其高效的一种解题方法.微元法当中的“微”主要指解题过程十分短暂,“元”则指独立性,也能够反映出解题过程,也就是说在整体当中划分出细微的局部,依据某些内在关联与规律,经过局部了解到物理试题,以完成解题.将微元法应用于物理解题过程,主要是对物理问题实施分析和解决,属于多种解题法中最有效的方法之一,其不仅可以使学生在具体解题过程中,深刻体会到从部分至整体的解题过程,而且还可以帮助学生有效掌握相关物理知识,从而使学生的解题水平与学习能力实现有效提高.

1 微元法应用的解题流程

第一步,取“元”.“元”是重要内容,解题的关键就是取“元”,如果不能保证取“元”的正确性,就会影响到学生自身的解题效果.因此,在取“元”时,需注重几个点:(1)取“元”时,要确保该计算过程是十分简单的,若取“元”难度相对较大,不建议运用微元法[1];(2)取“元”可经过不断的叠加,获得相应的结果,叠加可呈现在两方面,一方面是加权叠加,依次计算各“元”;另一个方面,则是确保取“元”后,可呈现全面且系统的知识体系,由此可知,取“元”经过叠加后,可代表整体.

第二步,模型化.当完成取“元”后,教师就需引导学生积极应用“元”,即模型化,其能够通过接近于相等或极限相等等各种方法,对问题的解决难度进行降低,以采取更加简单的方法,进行物理模型的构建,从而使物理问题的解决过程更加简单、高效[2].

第三步,求和.计算完“元”后,教师就需引导学生采用叠加求和,计算出相应的结果.一般来说,叠加计算的整个过程与数学知识之间是有着紧密关联的,这就要求学生学会运用相关数学知识及其求和公式进行求和.

2 微元法在高中物理解题中的应用策略

2.1 微元法在电磁感应问题解决中的应用

例1在光滑且水平的导轨上面放置一个金属杆,其质量为m,且导轨的间距为L,导轨一边连接的电阻阻值为R,其他的电阻均不考虑其阻值.此时,垂直导轨均匀的磁场,其强度是B,若金属杆朝右的初始速度是v0,若导轨有着足够的长度,求取金属杆在导轨上向右移动的最大距离是多少?

解析对金属杆的具体受力实施科学分析,重力为mg且支持力为N,因为金属杆朝右边移动时,所受的安培力会按照其自身的位置不断变化,这个时候,加速度就会逐渐降低,呈现出减速运动;而微元法的灵活应用,其主要是将解题的全过程,分解成同样的微小单元,且金属杆在各微小单元当中最初的速度是v,且各单元当中金属杆具体运动的时间是与0无限接近的,因此,可表示各个微小单元的金属杆均为匀速直线运动[3].因此,本题的解决关键是结合微元法,明确导体棒做加速度不断减小的减速运动.

解导体棒受重力、支持力以及向后的安培力;其中,感应电动势为:E=BLv

安培力为:F=BIL

依据牛顿第二定律,可得:F=ma

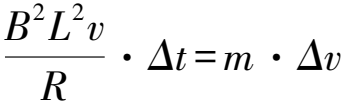
金属杆位于导轨上朝右移动的最大距离为:

2.2 微元法在运动力学问题解决中的应用

例2地面上经过v0的速度朝上竖直的抛出一个物体,其质量是m,现已知物体受到的空气阻力与速度成正比,物体的具体运动速率详见图1,求取:

(1)物体从最开始抛出到最后落地,空气阻力做的功有多少?

(2)物体抛出的一瞬间加速度为多少?

(3)物体处于t1的时候,高度为多少?

图1 物体空气阻力与速度图示

解析据题意可得,物体运动情形为:最初经过v0的速度不断向上做减速运动,受到朝下的重力与空气阻力的影响,在t1处为最高点时,其速率是0.接着,在下一秒实施下落,在这一阶段,受到了向上的空气阻力、向下的重力影响,当物体回到地面的时候,如果物体做匀速运动,落地的速率为v1,此时,可通过微元法加以求解[4].

所以,空气阻力所做的功为:

(2)因为空气阻力为:

f=kv

物体在实际落地前,做匀速运动,所以,mg=kv1;

如果物体抛出的时候,初始加速度是a0,则能得出:

ma0=mg+kv0

一些普通高校继续教育学院并没有意识到举办社区教育的重要性、紧迫性，还停留在成人学历教育层次上，对服务社区成员的社区教育存在着轻视、歧视和无视的错误认识。一些高校继续教育学院虽然认识到社区教育的重要性，却找不到介入社区教育的合适方式、途径和模式，无场地、无师资、无经费、无课程，思想上处于观望，行动上难以向前迈进。

又由于vΔt=Δh,所以,∑Δv=-g∑Δt-∑Δh

2.3 微元法在单棒切割问题解决中的应用

例3如图2,两个导轨是平行的,其所处的面和水平面之间的夹角是θ,两个导轨中间的距离为L,导轨上侧与电容器进行连接,电容是C,导轨处于均匀的磁场中,磁感应强度可达到B,磁感应强度方向与导轨是垂直的.导轨上放置个质量是m的金属棒,该棒能够顺着导轨逐渐下滑,当下滑的时候,需和导轨呈垂直状,并有切实的接触.已知,导轨和金属棒产生的动摩擦因数为μ,重力加速度是g.现将金属棒由导轨的上侧向下滑动,求:

(1)电容器电荷量和金属棒速度的关系;

(2)金属棒的速度与时间之间的关系.

图2 单棒切割图示

第(2)小问中,运用微元法,选择一段极短的时间Δt,金属棒位于该段时间中的速度变化量是Δv,电容器的电量具体变化量是ΔQ=BLCΔv,且导体当中的电流是I,依据牛顿第二定律,则得:

mgsinθ-μmgcosθ-BIL=ma

①

②

即金属棒的加速度不会出现改变,其做匀加速运动,金属棒的速度与时间之间的关系为:

综上所述,微元法运用于物理解题中,主要是通过事物的变与不变,让学生充分掌握相关物理定理与规律,将物理问题变得更加简单,以便于学生迅速理清解题思路,有效解决物理问题,从而使学生实现高效解题.