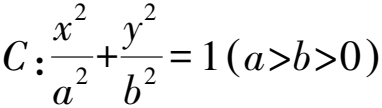圆锥曲线离心率的求解策略
李发明
(山东省泰安第一中学,山东 泰安 271000)

1 直接分析圆锥曲线的扁平程度
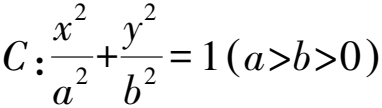



评注椭圆的离心率e∈(0,1),离心率越小椭圆越圆,离心率越大椭圆越扁.双曲线的离心率e∈(1,+∞),离心率越小张口越小,离心率越大张口越大.直接分析圆锥曲线的扁平程度有时能起到立竿见影的效果.
2 由几何关系构造等式求离心率

解析设|PF2|=x,则|PF1|=3x.


由余弦定理,得



评注充分挖掘题干中所包含的信息,寻找合适的几何关系,建立关于a,b,c的等式,求出离心率.
3 由几何关系构造不等式求离心率





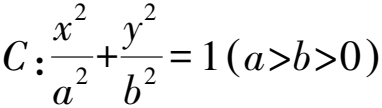
解析连接AF1,BF1,则A,F1,B,F四点构成平行四边形,设|FB|=x,则|FA|=2x,|AF1|=x.
所以x+2x=2a.








评注利用题干中包含的几何关系,建立关于a,b,c的不等式,求出离心率的取值范围.
4 解齐次方程(或齐次不等式)求离心率
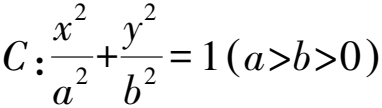
解析AP的垂直平分线过点F等价于在椭圆上存在点P使得|PF|=|AF|.
整理,得ac+2c2-a2≥0.
左右两边同时除以a2,得2e2+e-1≥0.

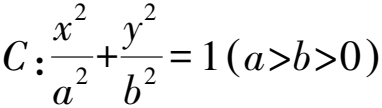


因为焦点F在正方形ABCD的外面,

即c2(a2+b2)>a2b2.
即c4-3a2c2+a4<0.
左右两边同时除以a4,得e4-3e2+1<0.


评注利用题干中包含的几何关系,建立关于a,b,c的等式(或不等式)之后,有时会得到一个关于a,c的齐次式,此时只需将等式(或不等式)两边分别除以a或a2或a4转化为关于e的方程(或不等式),解方程(或不等式)即可得e(或e的取值范围).解齐次方程(或齐次不等式)求离心率在高考及模拟考试中考查最频繁,地位最重要.
5 利用椭圆的参数方程求离心率
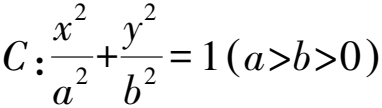
解析设P(acosφ,bsinφ),易知B(0,b).

即a2cos2φ+b2sin2φ-2b2sinφ+b2≤4b2.
即c2sin2φ+2b2sinφ+3b2-a2≥0.
令t=sinφ,t∈[-1,1],则c2t2+2b2t+3b2-a2≥0对t∈[-1,1]恒成立.





即-b4+2b2c2-c4≥0.
即-(b2-c2)2≥0,此时b=c,与b 所以a2cos2φ-c2+b2sin2φ≤ac对任意实数φ恒成立. 即c2cos2φ-c2+b2≤ac. 左右两边同时除以a2,得e2+e-1≥0, 解析题干所述符合椭圆的第三定义, 评注圆锥曲线的第三定义:平面内的动点到两定点A1(-a,0),A2(a,0)的斜率乘积等于常数e2-1的点的轨迹叫做椭圆或双曲线(实际上两定点关于原点O对称即可),当e∈(0,1)时轨迹为椭圆,当e∈(1,+∞)时轨迹为双曲线.利用圆锥曲线的第三定义求离心率在近几年的高考模拟考试中频繁出现,应引起足够重视. 故选ACD. 由余弦定理,得(2c)2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos60°. 两式相减,得 因为M(-3,2)为线段AB的中点, 所以x1+x2=-6,y1+y2=4. 所以切线AC的方程为y=k1(x+at). 切线BD的方程为y-bt=k2x. 解析不妨设点A在第一象限,记△AF1F2的内切圆的圆心为点M,圆M与x轴切于点N,由三角形内心的性质我们有 所以点N的横坐标为a. 所以点M的横坐标为a. 因为AF2与渐近线平行, 整理,得3c2-8ac+5a2=0. 所以3e2-8e+5=0, 评注求圆锥曲线的离心率(或离心率的取值范围)是高考的重点也是热点,问题的关键在于通过题干中的条件,寻找a,b,c所满足的几何关系,有时是等量关系,有时是不等关系,列出几何关系之后往往还需要消去b2,转化为关于a,c的等式(或不等式),进而求解.例15是典型的弦的中点问题,点差法是处理这类问题的利器;例16是具有相同离心率的椭圆方程的设法;例17与三角形内心的性质有关,这些特殊问题的特殊解法也是需要掌握的.
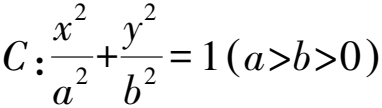




6 利用圆锥曲线的第三定义求离心率





7 椭圆与双曲线结合的问题


















8 求圆锥曲线的离心率杂题赏析