2023年全国乙卷(理科)第19题的多解探究
雷 誉
(湖北省咸宁市青龙山高级中学,湖北 咸宁 437000)
立体几何中的证明和计算问题是高中数学的热点和重点内容,具有一定的难度.本文以2023年全国乙卷的立体几何大题为例,从不同解题思路出发,拓展求解策略和思维角度,帮助学生掌握常见的解决立体几何问题的三大方法:几何法、坐标向量法和基底向量法,使其加深认识和提高效率.
1 真题再现


图1 三棱锥P-ABC
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
2 试题解析
思路1 证明立体几何中的平行和垂直关系的问题时,需要借助平面几何图形分析出线线平行或垂直关系.计算立体几何空间角的问题,需要运用几何性质作图找到所求的夹角,然后利用解三角形知识求解问题.
解法1(几何法) (1)如图2,过点A作AB的垂线AQ,延长BF交AQ于点Q,易得∠BOA=∠ABQ.
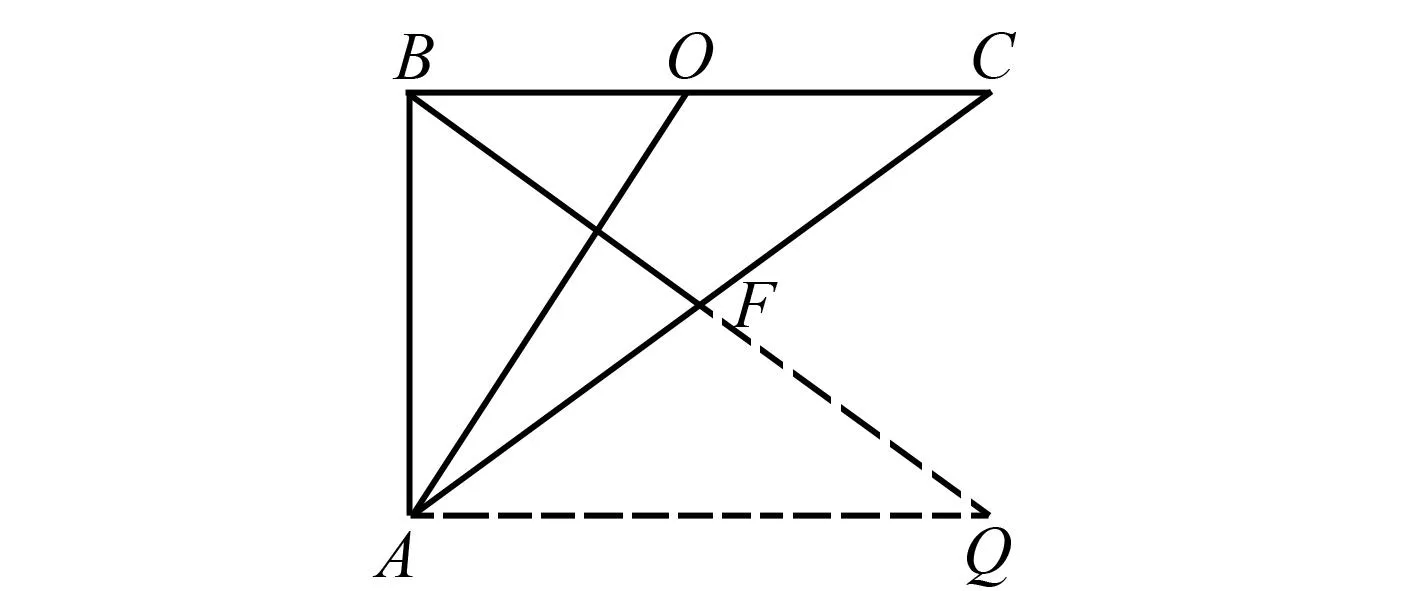
图2 平面ABC的几何法
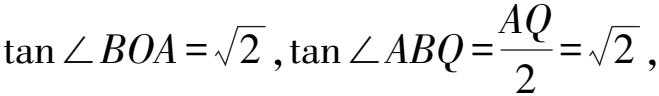

所以AQBC.
所以F为AC的中点.
由D,E,O,F分别为PB,PA,BC,AC的中点,

又EF⊄平面ADO,DO⊂平面ADO,
所以EF∥平面ADO.

所以OD2+AO2=AD2.
则OD⊥AO.
即EF⊥AO.
又AO⊥BF,BF∩EF=F,BF,EF⊂平面BEF,
则有AO⊥平面BEF.
又AO⊂平面ADO,所以平面ADO⊥平面BEF.
(3)记AO,BF交点为G,AD,BE交点为H,易得G为△ABC的重心,H为△PAB的重心.

则GH∥OD.
又OD⊥AO,则GH⊥AO.
又GF⊥AO,所以∠HGF即为二面角D-AO-C的平面角或∠EFB为二面角D-AO-C的平面角的补角.







点评几何法的难点是抓住已知条件找出几何关系,前两问是为了第三问作出二面角的平面角做准备.在破解立体几何问题的过程中,需要关注空间模型的几何特性,包括点线关系、线线关系、线面关系等.从平面视角可确定两线的特殊关系,为空间关系的探索做好基础[1].
思路2首先根据题目条件分析出三条两两互相垂直的直线,建立合适的空间直角坐标系,运用坐标法解决立体几何的证明和计算问题.
解法2 (1)同解法1.
(2)易得OF⊥BC,OP⊥BC,OF∩OP=O,则BC⊥面POF.



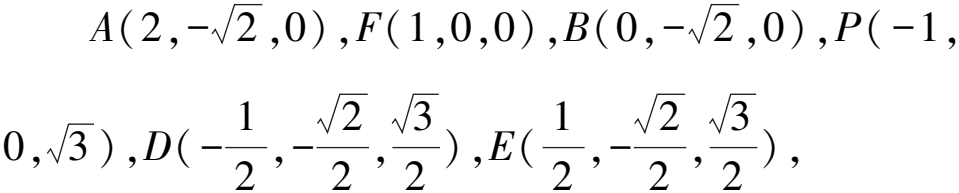
设面ADO的法向量n=(x1,y1,z1),则

设面BEF的法向量m=(x2,y2,z2),则


所以平面ADO⊥平面BEF.

图3 以O为坐标原点建系图4 以B为坐标原点建系
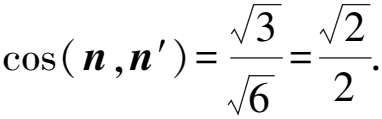



所以F为AC的中点.

所以EF∥平面ADO.
(2)设D(x,y,z),则

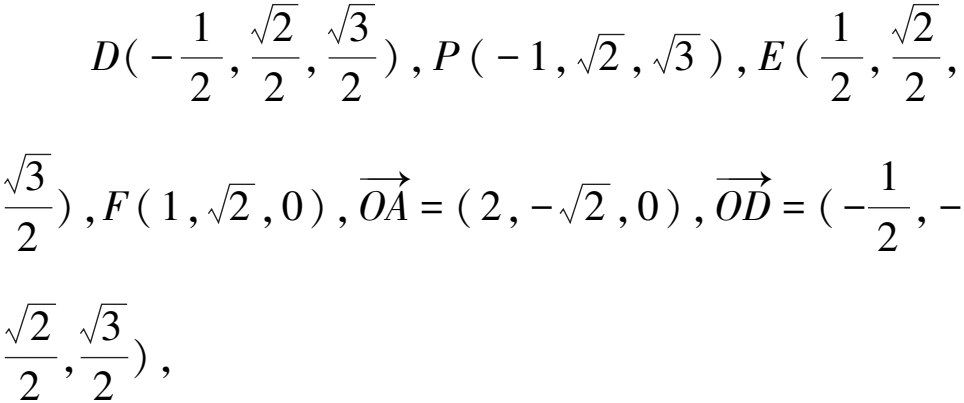


所以平面ADO⊥平面BEF.
(3)同解法2.
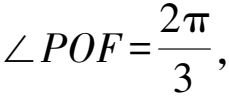
思路3若三条两两互相垂直的直线不容易找到时,可以选取长度和夹角已知的三个基向量为一组基底,运用向量运算解决立体几何的证明和计算问题.
解法4(1)连接DE,OF,设AF=tAC,则


所以EF∥平面ADO.

所以OD2+AO2=AD2.
则OD⊥AO,即EF⊥AO.
又AO⊥BF,BF∩EF=F,BF,EF⊂平面BEF,
则有AO⊥平面BEF.
又AO⊂平面ADO,所以平面ADO⊥平面BEF.







解得x2=2,y2=-1,z2=0.


所以平面ADO⊥平面BEF.

解得x3=1,y3=-1,z3=2.






在平时立体几何问题的训练中,要多从图形的几何特性去分析线线关系和线面关系,还要能利用好空间向量这个法宝,既可以建立合适的空间直角坐标系,还可以选取模长和夹角已知的向量为一组基底,将问题转化为向量运算.在解题过程中需要不断积累和总结,以帮助学生掌握数学思想方法和提高数学素养.

