一道开放性椭圆试题的探究与推广
栾 功
(南宁市第三中学,广西 南宁 530021)
《普通高中数学课程标准(2017年版2020年修订)》在高考命题建议中明确提出:命题时,应包括开放性问题和探究性问题,重点考查学生的思维过程、实践能力和创新意识[1].这一指导思想在近两年的各类考试命题中也得以体现,且较多集中在以数列和解三角形等知识为背景的结构不良问题上.而2022年一次西南大联考中圆锥曲线大题一改往日常态,以开放的探究型问题呈现,不论是试题的知识背景还是问题的呈现形式,都给考生耳目一新的感觉.
1 试题呈现
题目(2022届“3+3+3”高考备考诊断性联考)点M是圆A:x2+(y+1)2=16上任意一点,点B(0,1),线段MB的垂直平分线交半径AM于点P,当点M在圆A上运动时.
(1)求点P的轨迹E的方程;
(2)BQ∥x轴,交轨迹E于点Q(点Q在y轴的右侧),直线l:x=my+n与E交于C,D两点(l不过点Q),且CQ与DQ关于BQ对称,则直线l具备以下哪个性质?证明你的结论.①直线l恒过定点;②m为定值;③n为定值.
分析试题第(1)问考查了圆的简单几何性质与椭圆的定义,体现了试题的基础性;第(2)问以圆锥曲线共轭弦性质为背景设计了与动直线l有关的开放型问题,给考生创设了自主思考的情境,便于考生多角度、开放地思考问题,试题考查考生独立地对问题提出见解并进行论证的能力,综合性强,对学生直观想象、逻辑推理、数学运算等素养都有较高的要求.
2 解法分析
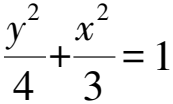


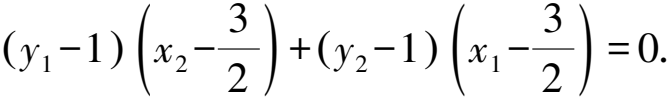
代入x1=my1+n,x2=my2+n,整理,得


(3+4m2)y2+8mny+4n2-12=0.

代入①式,得
整理,得4m2+(4n-8)m-2n+3=0.



点评解法1从直线l入手构图设参,通过对“直线CQ与DQ关于BQ对称”这一几何关系的坐标刻画,自然而然联系到运用韦达定理是解答这类问题的通性通法,其揭露的试题本质特征和内在联系为进一步探究其他解法、剖析试题本质、培养学生思维的深刻性和创造性等提供了基础.


(3+cos2α)t2+(6sinα+12cosα)t=0.





点评该解法从直线QC,QD的倾斜角入手,应用直线的参数方程解题,在几何关系代数化的过程中紧紧抓住直线QC,QD的逻辑结构的对称性,利用同构思想和三角恒等变换进行坐标运算,结构整齐、简洁明了.该解法不仅体现了参数法在解答解析几何问题中的重要作用,同时还开阔了学生的解题视野.

则变换后的椭圆方程为
整理,得
4x′2+3y′2+12x′+6y′=0.
②

4x′2+3y′2+(12x′+6y′)(px′+qy′)=0.
即(4+12p)x′2+(3+6q)y′2+(6p+12q)x′y′=0.
两边同时除以x′2,得
③
由于平移变换后点Q的坐标变为Q′(0,0),
故kQ′C′,kQ′D′是方程③的两个根.



由kQC+kQD=0,得
整理,得
3y1y2+3y1-3y2-4x1x2-6x1+6x2+6=0,
④
3y1y2-3y1+3y2-4x1x2+6x1-6x2+6=0.
⑤
④-⑤,得
6(y1-y2)-12(x1-x2)=0.


点评该解法的灵感源于对教材习题的理解,把椭圆的标准方程改写为第三定义的形式,在求解这类问题时收获意想不到的效果,同时彰显了坐标法的神秘与魅力.
上述四种解法从不同侧面阐释了直线l在运动过程中保持的规律性,即直线QC与QD的斜率之和为定值0时,直线CD的斜率为定值2.这一发现也启发我们进一步深入思考,如直线CD的斜率为定值是巧合吗?如果不是,它又与哪些量有必然的联系?
3 推广探究
思考1 在试题的解答过程中我们发现当kQC+kQD=0时,直线CD的斜率为定值,这个定值与点Q有关吗?


图1 思考1示意图
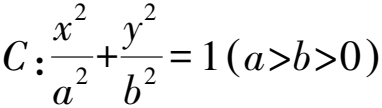
思考2由圆锥曲线定义的统一性猜想,抛物线与双曲线是否也有类似性质?
变式1点P(x0,y0)(y0>0)为抛物线C:y2=2px(p>0)上一定点,A(x1,y1),B(x2,y2)为抛物线C上两动点,若直线PA与PB斜率存在且互为相反数时,证明直线AB的斜率是非零常数.
证明因为点P(x0,y0),A(x1,y1),B(x2,y2)在抛物线y2=2px上,所以
⑥
⑦
⑧
⑥-⑦,得
(y0-y1)(y0+y1)=2p(x0-x1).


由kPA+kPB=0,得
即有y1+y2=-2y0.
⑧-⑦,得
(y2-y1)(y2+y1)=2p(x2-x1).



整理,得
4x′2-y′2+16x′-4y′=0.
⑨
设直线l′的方程为px′+qy′=1(其中p=4q),代入⑨式,得
4x′2-y′2+(16x′-4y′)(px′+qy′)=0.
即(4+16p)x′2-(1+4q)y′2+(16q-4p)x′y′=0.
即(4+16p)x′2-(1+4q)y′2=0.
两边同时除以x′2,得
⑩
由于平移变换后点Q的坐标变为Q′(0,0),
故kQ′A′,kQ′B′是方程⑩的两个根.
由于平移变换下不改变直线的斜率,
所以k1+k2=0.
推广2 设点Q(x0,y0)是对称轴平行于坐标轴的定圆锥曲线(包括圆、椭圆、双曲线和抛物线)C上一定点,A,B是C上两个动点,若直线QA,QB的斜率互为相反数,则直线AB的斜率存在时为定值,等于曲线C在点Q处切线斜率的相反数(当曲线C为双曲线时,点A,B在同支上).



由解法3可知,当kQC+kQD=0时,直线l′:px′+qy′=1中p,q满足p=-2q,直线l′的方程可写为q(y′-2x′)-1=0,当y′-2x′=0时,-1≠0,所以直线l′不过定点,从而直线l不过定点.如果我们尝试改变kQC+kQD的值或运算形式,直线l是否会过定点?



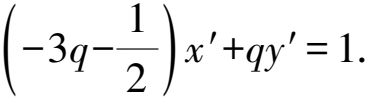









因此直线l′过定点(-12,6).

通过变式探究发现,当直线QC,QD的斜率之和、之积为非零常数时,直线CD恒过定点,同样也有一般性结论,在此不再一一罗列,感兴趣的读者可以进一步地发散思考与探究,在尝试提出更高探究性问题的过程中历练更高层次的思维,形成更深刻的理解和感悟.

