变化中找不变 探究中培能力
——2023届高三元月大联考理数20题的深入探究
王东海
(安徽省合肥市肥东县城关中学,安徽 合肥 231600)
在解析几何的四种圆锥曲线里,其中椭圆与圆是关系紧密的两个研究对象,它们的图形有着很强的对称性.另外椭圆中会生成很多圆,如蒙日圆、伴随圆、基圆和内切圆等,它们在性质上具有怎样的关系?再者椭圆中出现的扑朔迷离的变化中蕴含着哪些不变性?本文以一道2023届高三元月大联考圆锥曲线试题为例,通过对问题的解法探究、引申拓展、追本溯源,从而建构此类题的处理方法.
1 考题呈现

(1)求点P的轨迹方程.

2 解法探究




当直线l的斜率存在时,设直线l的方程为y=kx+m,且设A(x1,y1),B(x2,y2),再联立椭圆方程并消去y可得(3+4k2)x2+8kmx+4m2-12=0[1].
所以△=48(3+4k2-m2)>0,
即m2<3+4k2.




即7m2-12k2-12=0.

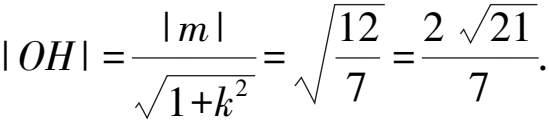
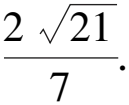
视角2 射线OA,OB过原点,故也可设出OA的方程,通过直曲联立可得A,B两点的坐标,最后用三角形等面积法可以求出|OH|的值.

又当直线OA斜率存在时,则设其方程为y=kx.联立椭圆C的方程并消去y得
(3+4k2)x2-12=0.

①

②


视角3 观察题目所给条件,有斜率之积为-1的条件,故可考虑使用齐次化法加以处理.
解析3 因直线AB不过原点,故设直线l的方程为mx+ny=1,且设A(x1,y1),B(x2,y2),
对已知椭圆方程3x2+4y2-12=0配凑得
3x2+4y2-12(mx+ny)2=0.
即(3-12m2)x2-24mnxy+(4-12n2)y2=0.
两边同除以x2,得

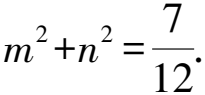
③

视角4 此题中直线OA,OB都经过原点这个定点,容易联想到直线的参数方程.

(3cos2α+4sin2α)t2-12=0.

由t的几何意义知:

品质得分在54.70以上的为优质一级烤鸭,市售优质烤鸭中检测到的9种杂环胺总含量水平为5 757.02~6 859.31ng·g-1。


视角5题中A,B两点都在椭圆上,故可以考虑利用椭圆的参数方程来设出A,B两点的坐标.


所以4cosαcosβ+3sinαsinβ=0.
从而16cos2αcos2β=9sin2αsin2β.
④
即16cos2αcos2β=9(1-cos2α)(1-cos2β).

又因OA2=4cos2α+3sin2α=3+cos2α,
OB2=4cos2β+3sin2β=3+cos2β,
故由三角形等面积法得


视角6 此题中直线OA,OB都经过原点这个定点,从而OA,OB与ρA,ρB相关联,因此使用极坐标方程相比参数方程更减少其运算量.
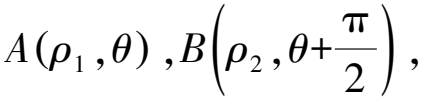





3 拓展推广
一题多解可以培养学生全面分析问题的能力、综合运用知识的能力,以及数学思维能力.教师不能只局限于对题目的具体解答,还应引导学生对问题进行深层次的探究及引申,充分挖掘题目的内涵和外延,使学生能够用更高的观点去看待问题.细品此题的结论,它对于一般的椭圆是否仍然成立呢?对于双曲线及抛物线有无类似的结论呢?此题是否可以引申产生其它结论呢?基于以上思考,我们可以得到以下几个一般性结论.
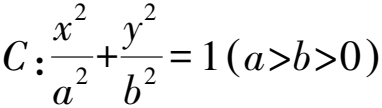
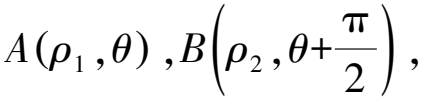





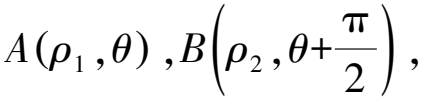



故原点到直线AB的距离为
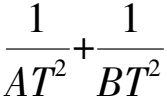
这里用直线的参数方程易证.略.



运用类比推理,对于抛物线,是否也有类似的结论呢?
结论6 已知抛物线C:y2=2px(p>0),A,B是异于顶点的两动点,且OA⊥OB,OM⊥AB,并与AB相交于点M,则点M的轨迹方程(x-p)2+y2=p2,且(S△AOB)min=4p2.

因为OA⊥OB,

解得t1t2=-1.
⑤
又因为OM⊥AB,

即x(t2+t1)+y=0.

⑥

由A,B,M三点共线,从而有
化简,得y(t1+t2)-2pt1t2-x=0.
将⑤⑥代入得到
x2+y2-2px=0.
即点M的轨迹方程为(x-p)2+y2=p2.
由上述推理知

即(S△AOB)min=4p2.







图1 结论8示意图
证明不妨设l与圆x2+y2=r2相切的切点为(rcosθ,rsinθ),则此切线方程为
cosθ·x+sinθ·y=r.
⑦
再设两条切线的交点M(x0,y0),则过点M作椭圆的两条切线,从而切点弦所在直线方程为
⑧
显然方程⑦⑧为同一条直线的方程,故有



