基于知识驱动及数据相关性的低压配电网户变关系识别

柳守诚,王淳,邹智辉,刘伟,陈佳慧,周晗

(南昌大学信息工程学院,江西 南昌 330031)

目前,高级量测体系(advanced metering infrastructure,AMI)广泛应用于低压配电网中,高级量测体系的量测数据能帮助工作人员有效掌握低压配电网的运行情况,对配电网进行分析并作出决策。随着社会高速发展,低压配电网现场接线日益复杂,现场设备的更新换代加快,用户所属关系更新的不及时、用户数据量的不断增大等易导致电力运营商难以及时掌握正确的配电网拓扑结构。因此,能够及时掌握并更新配电网拓扑结构成为目前国内外研究关注的热点问题。

当前,低压配电网广泛存在变-相-户关系记录问题[1-3]:本该属于变压器A的用户,信息管理系统中却显示该用户属于变压器B;某变压器的用户档案齐全,但又多包含了其他变压器的用户档案;某用户电表本应属于A相,现场档案记录却显示属于B相,或者直接丢失了该用户电表的相位记录等等。上述问题部分来自于用户所属关系在设备更新换代时发生改变而档案记录更新不及时;另一部分是因为现场接线复杂,难以辨别关系,人工记录失误。这些问题不仅影响低压配电网各类参数如线损、有功功率等的计算,进而对从业人员分析配电情况带来妨碍,而且对治理负荷不平衡、提高供电可靠性、降低损耗等工作展开带来干扰。

国内外研究者主要通过转移潮流[4]、相似距离[5-6]、最小二乘法[7-9]、载波通信[10]、机器学习[11-13]等方法针对变-相-户关系问题进行研究。文献[14]通过T型灰色关联度计算户与户、户与变压器的电压接近程度,同时利用时间这个因素,相较于传统的灰色关联度无须设置分辨系数,也不受电压极值的影响,再通过KNN算法准确归类可疑用户所属变压器。文献[15]针对相位标签容易出错的问题,提出一种新的谱聚类方法,使用AMI提供的电压时序数据校验了现有的用户相位标签,极大降低了误差,说明在AMI大数据的支持下,机器学习及相关理论在拓扑识别问题上有广阔应用前景。文献[16]在用户用电数据不完整的情况下,基于低压配电变压器的电压特性,推导出了低压配电网用户多维相关特性,并提出一种相户识别多维校准的方法,在实际算例中具有良好的适用性。

本文给出一种基于先验知识及数据相关性的户变关系识别方法。首先,以配电变压器某一相线为例,推导分析电压时序特性及相关先验知识。借助电压相关系数,确定初步的户变关系及嫌疑用户集合,再由分类矩阵和阈值系数向量确定近端用户集合。在此基础上,剔除嫌疑用户集合中的错误用户,对剩余嫌疑用户单独分析处理,实现户变关系及错误用户正确归类的问题。最后通过现场实际数据分析计算,验证了所提方法的有效性和准确性。

1 电压特性和先验知识

1.1 电压特性分析

以配电变压器的某一相线为例,通过推导节点电压的计算公式,分析用户电压特性。为方便计算和后续分析,对相线进行简化处理,具体包括:

1) 考虑到城市低压配电网的电缆经集中表箱分接入户,而农村用户电表的下引线的长度较短,因此忽略电表引线上的电压降落。

2) 不考虑线路中由分布式电源可能带来的反向潮流的影响。

如图1所示,任一节点m的电压为:

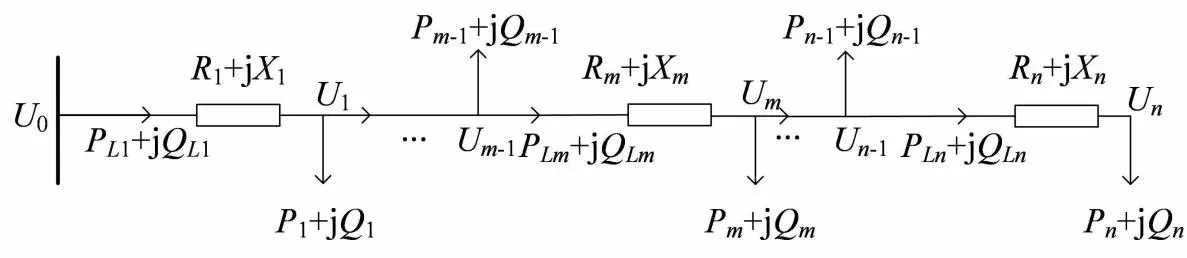
图1 配电变压器某一相线示意图

(1)

式中:Um表示m节点的电压值;U0表示配电变压器(以下简称“配变”)低压母线的电压值;PLi、QLi分别表示第i段线路的首端输入的有功功率和无功功率;n为低压配电网所含节点总数。

则t时刻节点m的电压为:

(2)

t时刻相邻两点的电压差为:

(3)

对任意相邻两时刻,电压的变化量为:

(4)

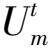
由式(2)及式(3)可知:

1) 线路上任意节点的某时刻电压值和该时刻配变低压母线的电压值、该节点到线路首端的各段线路阻抗、上游各段线路首端输入功率有关。

2) 同一时刻下,单电源相线沿电流流动方向,电压幅值总是在逐渐下降。

由式(4)可知:

1) 任意相邻时刻,同一节点的电压变化量与配变低压母线的电压变化量、该点上游各段线路阻抗、两时刻下上游各段线路首端输入功率、上游各节点电压幅值有关。

2) 同相同出线任一节点相邻时刻电压的变化量主要取决于上游各线段功率的变化量之和,即该出线的综合负荷特性。因此,不同相线综合负荷特性存在差异时,不同相线节点的电压时序曲线也应该存在差异。

在图1中,对于靠近配变低压母线的节点,由于其与低压母线的线路距离很短,线路的阻抗很小,使得式(4)的后半部分如式(5)所示近似等于0。

(5)

由式(4)及式(5)可以进一步得到靠近配变低压母线的节点m满足:

(6)

考虑到不同配变母线电压及负荷特性存在差异,因此可推断出:靠近配变母线的节点与所属配变母线的电压曲线的相似性最大。为此可考虑采用相关系数描述电压曲线的相似性。

相关系数是研究变量之间线性相关程度的量,反映的是变量之间相关关系的密切程度。常见的相关系数为皮尔逊相关系数,本文采用皮尔逊相关系数,计算公式为:

(7)

亦可写为:

(8)

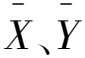
皮尔逊相关系数的值总是介于-1到1之间,|rXY|的值越大,说明X、Y之间相关性越高;|rXY|的值越小,说明X、Y之间相关性越低;当|rXY|为0时,说明X和Y不相关。

皮尔逊相关系数的阈值标准如表1所示。

表1 皮尔逊相关系数的阈值标准

1.2 先验知识

由1.1节的分析可得先验知识1:靠近配电变压器的用户与所属的配变低压母线之间的电压相关系数值最大。

同配变用户之间电压相关性较大,而不同配变用户之间电压相关性较小;因此,同配变用户之间电压相关系数集合均值较大,而不同配变用户之间电压相关系数集合均值较小。同配变用户之间的电压相关系数集合波动较大,其集合的方差较大。不同配变用户之间的电压相关系数集合波动较小,其集合的方差较小。由此可得到先验知识2:同配变的用户之间的电压相关系数集合的均值和方差较大,不同配变的用户之间的电压相关系数集合的均值和方差较小。

2 户变关系识别分析

户变关系的识别问题不仅要解决用户隶属的配变的问题,当存在某些配变用户档案混淆到另一配变用户档案中,还需要将这部分用户重新划分到正确配变下。为此,本文假定已知两相邻配变的用户信息,但信息老旧待更新,本文方法解决如何更新用户档案并将错误归属用户重新纳入到正确配变的问题。本章针对识别过程中存在的问题逐步展开分析。

2.1 近端用户

由先验知识1可知,对于靠近配变的用户即近端用户,确定其所在配变只需比较用户电压与配变低压母线电压之间的相关系数值,相关系数最大值对应的配变即为该用户所属配变。所以识别户变关系应首先确定近端用户集合。

近端用户集可以根据已知档案信息,同时按照计量周期内采集到的电压均值的大小顺序排列用户,再选取一定比例的用户作为近端用户。这种方法对于所有用户属于同一支线时有效,如果配变下有多个分支线,则该方法得出的近端用户集会出现偏差。

为解决上述问题,可以由配变用户档案信息和用户电压数据,进一步确定配变各个分支线的用户,再将各个分支线的用户按电压大小顺序重新排列,选取合适的阈值系数,组成阈值系数向量,这样就可以分别确定各个分支线下的近端用户,从而得到近端用户集合。这样获得的近端用户集合准确度更高。

2.2 分类矩阵

确定配变近端用户集合需要知道配变的用户和分支线之间的关系,为此提出构造一个分类矩阵Z,其每行各存储同一分支线下的用户,其他部分用0填充,该矩阵可由计量周期内用户电压数据计算得出。分类矩阵Z算法流程如图2所示。

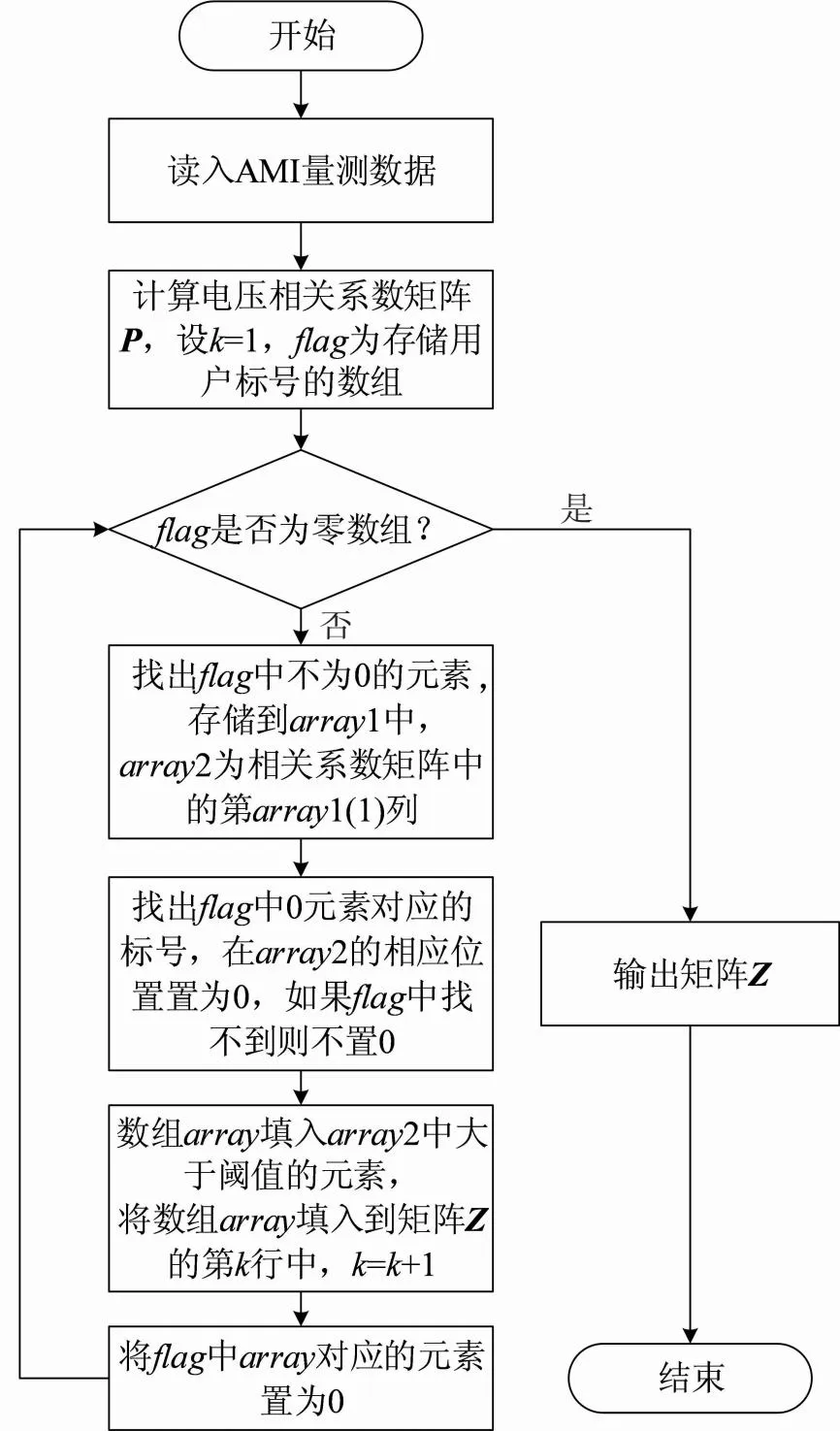
图2 分类矩阵Z计算流程

具体步骤为:

1) 读入AMI量测数据。

2) 计算用户间的电压相关系数,得到电压相关系数矩阵P,设k=1,flag为存储用户标号的数组。

3) 找出flag中不为0的元素,存储到array1中,array2为相关系数矩阵中的第array1(1)列。

4) 找出flag中0元素对应的标号,在array2的相应位置置为0,如果flag中找不到则不置0。代表已经归类的标号不应被重复考虑。

5) 数组array填入array2中大于阈值的元素。

6) 将数组array填入到矩阵Z的第k行中,k=k+1。

7) 将flag中array对应的元素置为0,代表这些用户已经分类完毕,然后判断flag是否为零数组,若是则退出循环,否则返回步骤3)。

8)输出矩阵Z,算法结束。

2.3 非近端用户

由先验知识2可知,对于非近端用户,可通过检测用户和各配变用户的电压相关系数集合的均值和方差,同一个配变的用户相关系数集合的均值和方差较非同一个配变的用户大。

3 基于先验知识和数据相关性的户变关系识别

综合以上分析,本文给出一种基于先验知识的户变关系识别方法,该方法假定已知相邻配变的用户档案,结合已知的用户档案信息,找出错误归属的用户及其正确的归属关系。以2个相邻配变为例,具体步骤如下:

1) 由配变低压母线和用户的计量点处获取计量周期内电压数据,构建计量点电压数据矩阵Us,基于计量点之间的电压相关系数值,得到电压相关系数矩阵R:

(9)

式中:R1为N1维的方阵,表示的是两配变低压母线间电压相关系数矩阵;N1表示两配变低压母线总数;R2为N1×N2维矩阵,表示的是两配变低压母线和用户间电压相关系数矩阵;R4为N2维的方阵,表示的是两配变用户间的电压相关系数矩阵;N2表示两配变的用户总数。

2)R2中的任一列向量即为任一用户和两配变低压母线的电压相关系数值,列向量中的最大值对应的配变为该用户的初步归属配变。

3) 将已知的配变用户档案信息和步骤2)中得到的初步户变关系做比对,若存在关系不一致的用户,则纳入嫌疑用户集合λ中。

4) 根据2.3节中所提步骤,由配变用户档案信息和用户电压数据可得分类矩阵Z,对于分类矩阵中的每一行用户,根据原始电压数据计算计量周期内电压平均值,按从大到小重新排列,根据每一分支线下户与户之间的电气距离的远近,选取合适的阈值系数向量η,由此可得到近端用户集合N。

5) 嫌疑用户集合λ和近端用户集合N取交集,得到错误用户集合W,这部分用户集合的户变关系以步骤2)中所得的户变关系为准,同时从嫌疑用户集合λ中剔除错误用户集合W,λ更新为λ′。

6) 对于λ′中的每个嫌疑用户,从R4中提取与两配变非嫌疑用户间的电压相关系数值,并计算每一配变的电压相关系数集合的均值和方差。

7) 比较步骤6)中计算出的均值和方差数值,嫌疑用户所属的配变总是数值较大的那个配变。

4 算例分析

以南昌市2个相邻配变的用户归属作为实例,对所提方法进行验证。配变1一共136个用户,配变2一共232个用户。选取采集时间间隔为15 min,计量周期为1 d,每个用户96个采样值。选取阈值系数t=0.5。假定配变1中的用户6、13、55、66、94、100、101的记录档案错误混入了配变2的用户档案中。

根据本文所述方法,首先构建计量点电压数据矩阵Us。三相用户视为3个独立的单相用户,即A、B、C三相视为独立的单相。由电压矩阵Us,可得电压相关系数矩阵R。

提取R2中与错误用户有关的部分如表2所示,其中A1、B1、C1分别为配变1低压母线的A、B、C三相,A2、B2、C2分别为配变2低压母线的A、B、C三相。

表2 电压相关系数矩阵中的错误用户部分

分析表2可知:对于用户6,电压相关系数最大值对应的配变低压母线为C1,由此初步判断该用户所属配变为配变1,其他用户的归属同理可得。与设定的错误用户6、13、55、66、94、100、101之间电压相关系数值最大的配变低压母线均在配变1。对比已知的配变档案信息可知,记录的档案信息与根据电压相关系数矩阵初步判断的关系并不一致,因此将用户6、13、55、66、94、100、101纳入嫌疑用户集合λ中。

为得到配变1近端用户集合N,需确定配变1各分支线的用户分布。根据2.3节中所提步骤,由配变1用户电压数据可得分类矩阵Z。由分类矩阵得各分支线的用户分布如表3所示。

表3 配变1用户分布

本文选取阈值系数向量η=[0.5,0.5,0.5,0.5,0.5]T,对于每一分支线用户,求出1d内该分支线用户的电压平均值,再依据电压平均值降序排列次序及对应阈值系数,可得近端用户集合N。

查表4知,嫌疑用户6、13、55、66、94、100、101中,用户6、13属于近端用户集合N,由表2计算结果可知用户6、13均属于配变1。而用户55、66、94、100、101均不属于近端用户集合N,因此用户55、66、94、100、101仍属于嫌疑用户,嫌疑用户集合更新完成。此时,从电压相关系数矩阵中的R4中提取嫌疑用户55、66、94、100、101与非嫌疑用户集合之间的电压相关系数值,并计算均值和方差,如表5、表6所示。

表4 近端用户集合

表5 均值序列

表6 方差序列

由表5、表6知,嫌疑用户55、66、94、100、101与配变1非嫌疑用户之间的电压相关系数均值和方差均大于与配变2非嫌疑用户之间的电压相关系数均值和方差。由此判断这些用户应属于配变1,这与真实户变关系相比较结果一致,证明了本文所提方法的有效性和可行性。

5 结论

AMI测量体系为管理运行人员提供了海量用户端数据,充分分析利用这些数据,分析变-相-户关系,有利于实现精细化管理,满足当前对配电网自动化的需求。

本文针对目前低压配电网用户拓扑识别难、更新慢的问题,给出一种基于先验知识的配电网户变关系识别的方法。通过配变低压母线和用户间电压相关系数确定初步户变关系,并得出嫌疑用户集合,再借助分类矩阵及阈值系数向量精准确定近端用户集合,进而更新嫌疑用户集合,最后分析剩余嫌疑用户相关性均值、方差判据,实现低压配电网户变关系识别及错误用户正确归类的问题。算例分析表明,本文所提方法对于用户所属配变识别及错误纠正有较高的准确率,尤其在近端用户的选取上更加精准灵活,可针对实际分支线情况做出不同的处理。本文工作对于后续进一步展开用户用电行为分析、三相不平衡治理、供电恢复等深入应用具有参考意义。