基于BP神经网络的斜拉索损伤识别方法

林友勤,郑学善,余印根,王志俸

(1.福州大学土木工程学院,福建 福州350116;2.福建省高华建设工程有限公司,福建 福清 350301;3.福建省永正工程质量检测有限公司,福建 福州 350001)

改革开放以来,我国经济快速发展,桥梁网络建设不断扩大。然而桥梁在使用的过程中由于外界环境、交通荷载、疲劳等因素的作用,会引起材料的老化和结构承载能力的降低,这一直都是影响结构的安全性和适用性的重要问题。对于斜拉桥而言,拉索在服役过程中是相互协同工作的,当某一根拉索发生损伤时,会引起整个拉索的索力发生一定的变化。那如何利用智能算法将索力变化与结构损伤建立起某种关系,从而实现通过索力的变化来对结构的损伤进行识别并作出全面综合判断和评估值得进一步探索。

人工神经网络(artificial neural network,ANN)是从信息处理角度对人脑神经元网络进行抽象,建立某种简单模型,主要的用途是做数据处理和各种参数拟合。根据环境的变化,对权值进行调整,改善系统的行为,建立起大数据之间的相互关系,最终达到数据处理的要求。神经网络具有强大的计算能力、联想能力、适应性、容错能力和自组织能力,因而它在结构损伤识别领域受到了广泛的关注和研究。在众多神经网络中,BP神经网络应用最为广泛[1]。BP神经网络具有非线性映射、自我组织和并行处理等特点[2-3],特别是在大数据处理和解决复杂问题能力方面与其他传统诊断方法相比具有很大优势,在结构损伤识别中得到了有效的应用[4-6]。

李忠献等[7]用自组织竞争神经网络迅速准确地识别出子结构发生损伤后,再通过BP神经网络所建立的结构损伤识别方法,能够进一步准确识别子结构中结构损伤的位置和程度。杨杰等[8]通过固有频率与拉索损伤的对应模式,建立BP神经网络对斜拉桥拉索损伤识别定位,但对于损伤程度的识别不敏感。孙宗光等[9]在已经确定了结构损伤区域的情况下,应用BP神经网络实现了结构的损伤位置及其损伤程度识别的方法。谭冬梅等[10]将能量累积变异值作为特征值,再将AdaBoost算法和BP神经网络相结合,在有噪声的情况下,仍可有效地识别出大跨斜拉索的损伤程度。

合理的损伤指标是进行拉索损伤识别的关键,这方面也开展了相关研究。闫维明等[11]通过计算索力在最不利荷载效应时相对恒载索力值的变化,确立吊索与主缆的索力预警阈值,结合对索力异常值的成因分析,确立悬索桥的损伤预警流程。李延强等[12]通过斜拉索张力指标实现了对斜拉桥主梁不同位置、不同程度单点损伤的识别。Hua等[13]通过索力变化来检测桥梁主梁是否发生损伤,结果表明当使用无噪声索力时,可以正确识别桥梁主梁中的损坏位置和损坏程度,在测量噪声低的情况下也能对结构的损伤进行良好的识别。

可以看出,BP神经网络可以对结构损伤进行有效的识别,索力是拉索损伤识别的常用指标,但其作为一个绝对量,通常只针对所研究的某个桥梁,不具有通用性。此外,拉索损伤还会引起其他拉索索力的变化,多根拉索的损伤则会引起更复杂的变化。针对这些问题,本文以1座斜拉桥单根和2根拉索损伤识别为研究对象,尝试以无量纲的索力变化率作为拉索损伤识别指标,结合BP神经网络模型,进行大跨度斜拉桥的拉索损伤识别方法研究。

1 BP神经网络

神经网络的分类方式有学习方式、时间特性、模型结构等,从学习方式可分为监督学习、无监督学习以及半监督学习;从时间特性可分离散型与连续型;从模型结构角度分类是最为常见的分类形式,将神经网络分为前向网络和反馈网络(图1)。BP神经网络属于一种按照误差逆向传播算法训练的多层前馈神经网络,它包括了输入层、隐含层、输出层,通过正向传播和误差反向传播,对各层的权值进行不断的修正,直至网络误差平方小于预先设定的阈值,是一种有导师学习的网络模型[14]。

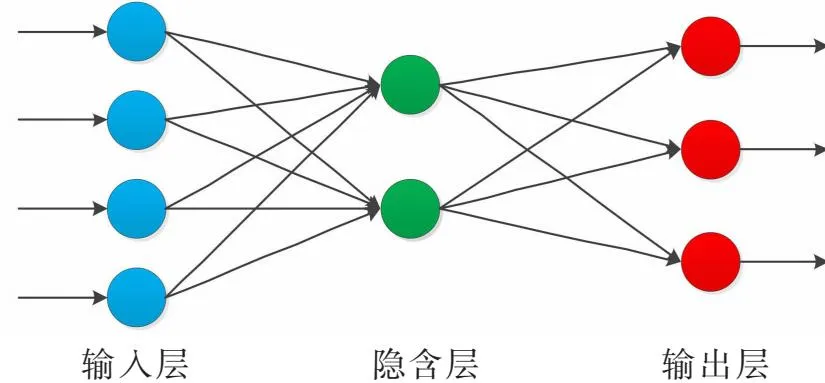
(a) 前向网络

1986年,McClelland和Rumelhaart定义了δ规则,其核心内容就是计算目标值与计算值的差值,通过不断地调整函数单元之间的连接强度来减小这个差值。

(1)

首先定义输出与期望输出之间的平方误差函数E为

(2)

如有要以最快的速度降低误差的话就是Wj应该与误差的负梯度成正比

ΔWj=-η∇E

(3)

其中误差梯度为

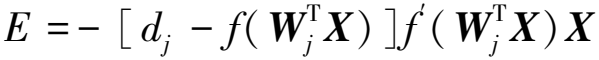
(4)

代入可得

(5)

进而得到ΔWj中的分量调整公式

(6)

2 斜拉桥模型建立与验证

2.1 工程背景

模拟1座双塔双索面半漂浮连续组合梁斜拉桥(图2)。桥梁的主跨布置为(32.9+115.4+340.0+115.4+32.9) m,全长为636.6 m。斜拉索为双索面结构,共104根拉索,拉索均采用OVM250系列环氧涂层钢绞线,标准强度为1 860 MPa,塔上索距0.6 m,梁上索距3.5 m,与索塔和主梁均采用钢锚箱锚固。主梁采用的是Q345C的单箱三室扁平流线型栓焊钢箱梁,桥面宽为32.4 m,桥面坡度为2%,纵向梁和横梁是由接头、高强度螺栓相连接。索塔采用的C50混凝土,塔柱的截面形式为单箱单室的空心截面,塔底左右塔柱中心间距35.6 m,总高为96.54 m。桥面与钢梁采用剪力螺栓连接。

图2 某斜拉桥现场照片

2.2 有限元模型建立

利用有限元软件ANASYS建立斜拉桥的实体模型,模型索力采用竣工后成桥索力定义。其中,1)采用Beam188单元对有限元模型中的纵梁、横梁和索塔进行模拟。2)采用Shell63板壳单元对桥面板进行模拟。3)桥梁的二期恒载直接转换成质量块,采用Mass21单元进行模拟,设置每个质量元在XYZ3个平动方向的质量为8 013.25 kg。4)支座用Combin14弹簧单元模拟。5)承台采用的是Solid45实体单元进行模拟,将墩底的每个节点的6个自由度全部约束。

全桥斜拉索共有104根,单侧52根,从南至北方向定义拉索编号,右侧依次为R1～R52,左侧依次为L1～L52,成桥左右对称拉索的索力是相同的。在ANASYS斜拉桥模型中的拉索初始应力是通过定义拉索的初应变所得到[15]。斜拉桥模型单元数13 060个,节点数总计58 221个。基本材料参数见表1。

表1 结构模型材料参数

2.3 模型验证

为验证斜拉桥ANASYS有限元模型(图3)的准确性,通过对有限元模型计算频率和桥梁的实测频率值进行比较,从表2可知,在竖向、横向、扭转这3个振动的方向的最大频率值误差为11%,在可允许误差范围之内,斜拉桥ANASYS有限元模型与实际结构相逼近。

表2 大桥模态参数

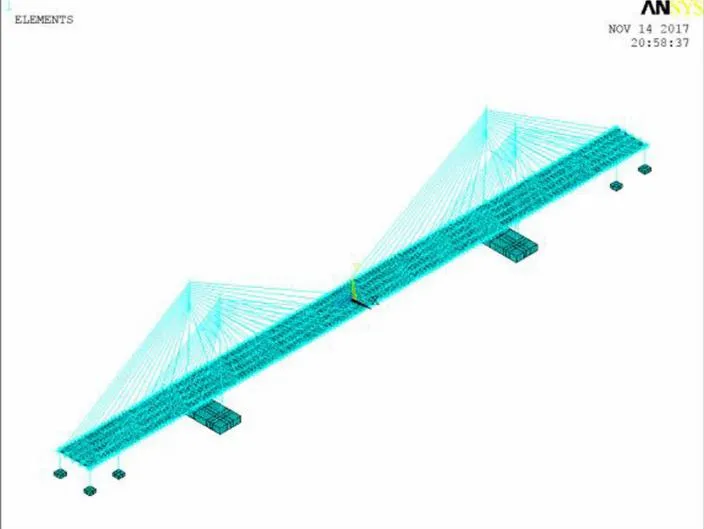
图3 斜拉桥有限元模型

3 斜拉索损伤识别

3.1 损伤指标的定义

在大跨度斜拉桥中,拉索发生损伤的同时所引起索力的变化也是十分显著的,将索力的变化与智能算法相结合运用于斜拉桥拉索的损伤识别具有更加实际的工程意义。定义拉索损伤指标索力变化率[16]见式(7)。

(7)

式中:RCOF、T、T′分别表示为索力变化率、未发生损伤时的拉索索力、发生损伤时的拉索索力。

通过拉索发生损伤前后的索力的变化计算得出全桥拉索的索力变化率,建立索力变化率与结构损伤的BP神经网络模型,进而可根据拉索的索力的变化来判断拉索损伤的位置和损伤程度。

3.2 斜拉索损伤识别流程

基于BP神经网络的拉索损伤识别过程可分为以下3个部分:

1)获取样本数据库。建立斜拉桥基准有限元模型,通过模拟拉索在发生不同损伤情况下的索力变化率以及拉索的损伤位置和损伤程度,以此作为样本数据库。

2)建立BP神经神经网络。以索力变化率为输入向量,相对应的损伤位置和损伤程度为输出向量,对样本进行训练,通过不断地迭代和修正得到了较为精准的BP神经网络系统。

3)实际桥梁的验证。在不同的外界激励下对实际桥梁的拉索进行振动测试,获取到的振动信号进行频谱分析,计算出拉索的实际索力,进而得到作为BP神经网络的输入向量的索力变化率,最后得到桥梁发生损伤及损伤的位置和程度,具体流程见图4。

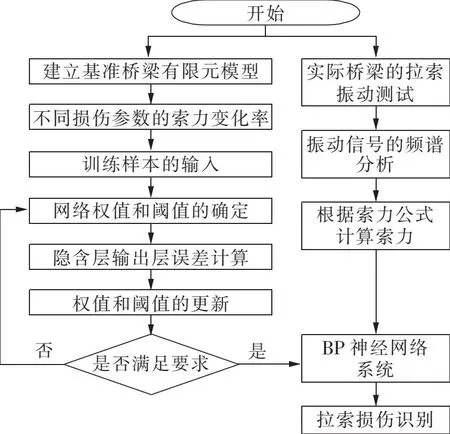
图4 斜拉桥神经网络损伤识别流程

3.3 BP神经网络的输入向量

在斜拉桥拉索损伤识别当中,由于该斜拉桥拉索是相互对称,故拉索损伤的模拟方式选取26根拉索进行分析,输入向量和输出向量均为26维,输入向量代表的是26根拉索的索力变化率,输出向量为26根斜拉索相对应的损伤程度和损伤位置参数。现模拟单根拉索损伤程度依次为弹性模量损失为0、10%、20%、30%、40%、50%、60%、70%、80%、90%这10种损伤,共有26×10=260个工况。2根拉索损伤是从拉索L1～L13中选取2根拉索,共78组,每组拉索的损伤程度分别为弹性模量损失40%、40%,40%、80%,80%、40%和80%、80%,总共有312个工况。总计572个拉索损伤工况数据作为神经网络模型的输入向量,图5列出了斜拉桥在单根拉索L1、L2、L5、L6在损伤程度为0、10%、20%、30%、40%、50%、60%、70%、80%、90%时的索力变化率数值和2根拉索L11、L12分别发生80%、40%与L9、L12分别发生80%、80%损伤时拉索的索力变化率,X轴、Y轴、Z轴分别表示的是损伤程度D、拉索编号n、索力变化率RCOF。

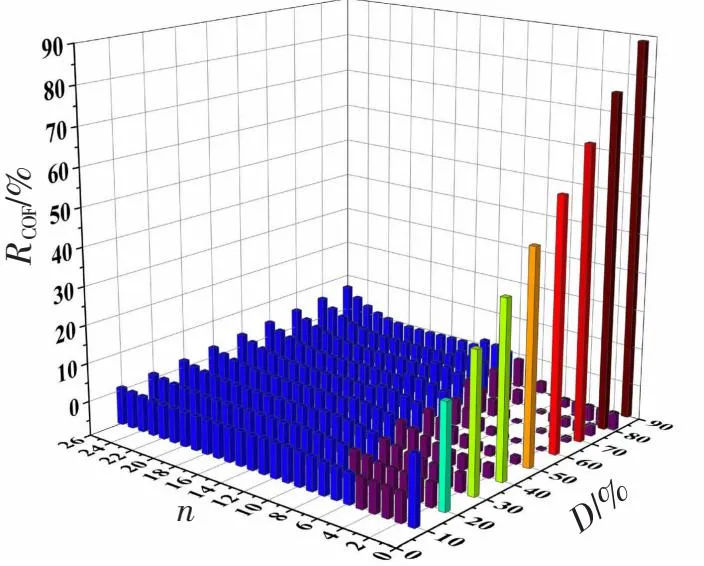
(a) L1拉索损伤

3.4 BP神经网络的建立

通过对有限元的模型修正,得到较为精准的有限元模型,为获取拉索发生损伤时的样本数据库,则通过降低拉索的弹性模量来模拟拉索损伤,通过上述式(7)所定义的索力变化率,构建出单根拉索发生损伤和2根拉索发生损伤时的索力变化率数据库,以编号为L1～L26的26根拉索的索力变化率作为神经网络的输入向量I,见式(8),拉索损伤位置和损伤程度则作为输出向量O,见式(9),最终建立起较为精准的BP神经网络模型(图6)。

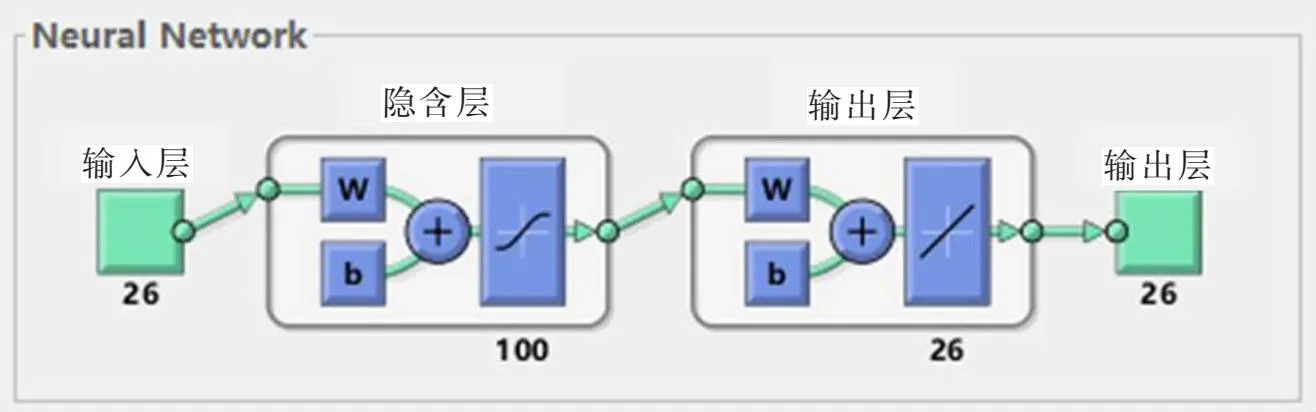
图6 神经网络的建立

I={RCOF1,RCOF2,…,RCOF25,RCOF26}

(8)

O={k1,k2,…,k25,k26}

(9)

通过多次训练发现,当神经网络隐含层的节点数量为100层时该模型运行效果最佳,建立26×100×26的BP神经网络模型。首先按照LM最优化算法的网络对已构建的样本数据库进行训练,之后再做进一步的损伤位置和损伤程度的识别。本文BP网络结构中采用MSE函数来对网络的性能进行评估,学习函数选择的是梯度下降动量函数Learngdm,第1层和第2层节点函数分别为双曲线正切S型传递函数Tansig与线性传递函数为Purelin。设置最大迭代步数为1 000步。具体训练函数参数见表3。

表3 训练函数参数

使用建立的BP神经网络对数据进行训练,网络模型计算到第16次,误差不再减小,当达到了最大失败次数6次,停止训练。对已经训练完成的神经网络取名称为BPNET。

在BPNET中样本数据库的设定为8：1：1,即80%为训练集,10%为验证集,10%为测试集,从神经网络计算误差结果(图7)可以看出,训练集、验证集、测试集、全部数据集的相关系数均在0.95以上,且测试集的相关系数达到了0.977 69,表明网络训练效果较好,误差较小,完全能够满足工程要求。

预测值

3.5 BP神经网络的识别结果

为了更加清晰地表达神经网络的识别结果和实际损伤程度,随机选取了6种单根拉索发生损伤和2种2根拉索发生损伤的工况对识别结果进行进一步的量化分析。由表4可知,对于随机选取的6种单根拉索L7、L1、L16、L20、L11、L4发生损伤的工况,损伤识别误差在5%以内,并且最小损伤识别误差仅为0.2%;随机选取的2根拉索L6/L12与L2/L3发生损伤工况,损伤识别误差稳定在6%以内,最小的损伤识别误差为1.2%;同时,对比2根拉索发生损伤识别时的效果和单根拉索发生损伤时的识别效果可知,本文中所训练的BP神经网络对单根的拉索的识别效果会略优于2根拉索发生损伤时的识别效果,但误差都在可允许范围之内,基本上能够满足实际工程的需求。

表4 拉索损伤结果

4 结论

本文建立了斜拉桥有限元模型,以索力变化率为损伤指标,基于BP神经网络对单根拉索和2根拉索损伤识别,结果如下:

1)采取降低弹性模量的方法模拟拉索损伤,利用修正后的有限元模型,得出拉索索力在自重作用下的变化值,结果表明,索力变化率对拉索损伤具有很好的损伤敏感性,可作为实际桥梁的损伤识别指标。

2)构建不同拉索和不同损伤程度下的索力变化率的样本数据库,建立基于LM算法的BP神经网络模型,最终的模型损伤识别结果的相关系数均在0.95以上,说明损伤识别结果准确。

3)任意选取8个损伤工况,对建立好的神经网络模型进行验证,结果表明单根拉索的损伤识别误差在0.2%～3.8%,2根拉索的损伤识别误差在1.2%～5.4%以内,能够满足工程要求,表明BP神经网络模型可以应用于单根或多根拉索的损伤识别。