基于自适应竞争学习的教与学优化算法
王培崇,冯浩婧,李丽荣
基于自适应竞争学习的教与学优化算法
王培崇1,冯浩婧1,李丽荣2*
(1.河北地质大学 信息工程学院,石家庄 050031; 2.河北地质大学 艺术学院,石家庄 050031)(∗通信作者电子邮箱jjj10300824@163.com)
针对求解较高维度优化问题时教与学优化(TLBO)算法容易出现早熟、解精度降低等问题,提出一种自适应竞争学习教与学优化算法(ITLBOAC)。首先,在“教”算子中引入非线性变化的权重参数,以决定当前个体自身状态的保持能力以及调整当前个体向教师学习的态度,从而使当前个体在早期更多地向教师学习,以迅速提升自身状态,而后期更多地保持自身状态,以减缓教师对它的影响;其次,以生态学协同竞争机制为基础,引入基于近邻个体间的自适应竞争的“学”算子,从而使当前个体选择它的近邻个体,并且让个体们从协作演化逐渐过渡到竞争学习。在12个Benchmark测试函数上的测试结果表明,相较于其他4种改进TLBO算法,所提算法具有更好的解精度、稳定性和收敛速度,同时相较于TLBO算法有大幅提升,验证了所提算法适合于求解较高维度的连续型优化问题。选择压缩弹簧和三杆桁架设计问题进行测试的结果表明,ITLBOAC获得的最优值分别比TLBO算法下降了3.03%和0.34%。可见,在求解约束工程优化问题时,ITLBOAC同样值得信任。
教与学优化;自适应学习;竞争学习;洛特卡-沃尔泰拉模型;约束工程优化问题
0 引言
教与学优化(Teaching-Learning-Based Optimization,TLBO)算法[1]通过模拟生活中的班级教学过程实现对问题解空间的启发式搜索,具有原理简单、参数较少和模拟容易实现等优点,已经被成功应用于车间作业调度[2]、供水量预测[3]、物流配送优化[4]和图像分割[5]等领域。
与其他典型群智能算法一样,TLBO算法同样存在数学基础薄弱、收敛性分析困难等问题,在求解较高维度的问题时,后期容易出现提前收敛、收敛变慢和解精度降低等现象[2]。为了提升算法的性能,许多学者从多种角度提出了不同的改进思路:Chen等[6]提出了一种改进TLBO算法(Improved TLBO algorithm, ITLBO),在“学”阶段,个体向教师个体和随机选择的近邻个体学习,在自我学习阶段,个体根据自己的梯度信息更新位置,或根据教师个体和种群平均状态更新位置。Zou等[7]提出了一种具有动态群策略的教学优化(TLBO with Dynamic Group Strategy, DGSTLBO)算法,在“教”阶段,个体能够向它所在组的平均值学习;在“学”阶段,个体能够在它所在组内进行随机学习或量子行为学习,每隔一定代数,进行动态重组,提高了种群的多样性。Li等[8]提出了一种混合差分进化的自适应教学(hybrid Adaptive TLBO and Differential Evolution, ATLDE)算法,学生基于概率自适应地选择“教”和“学”算子,在“教”算子中通过引入自适应教学因子(Teaching Factor, TF)强化优秀学习者在该阶段的开发能力,差异演化(Differential Evolution, DE)算法则被嵌入“学”算子,以提高群体多样性。高昊等[9]提出了一种基于协同变异与莱维飞行策略的教与学优化算法(Equilibrium-Lévy-Mutation TLBO algorithm, EMTLBO),以多个精英个体均衡引导种群进化,并通过自适应Lévy飞行策略和变异算子逃逸策略,赋予个体逃离局部最优的约束;实验结果表明,该算法具有较好的全局收敛性和解精度。翟志波等[10]提出了利用个体的拉普拉斯分布扰动机制拓展对解空间的搜索,并采用鲍德温学习效应标识有前途的解,使算法更具有竞争性,算法被命名为LBTLBO(TLBO algorithm based on Laplace distribution and Balwin learning effect)。何佩苑等[11]从人类的认知心理角度出发,提出融合认知心理学的改进TLBO算法(Cognitive Psychology TLBO algorithm, CPTLBO),在“教”和“学”两阶段,分别加入弱势学生的学习和教师引导机制,并添加群体的自我调整学习机制,较好地避免了算法早熟。欧阳城添等[12]提出了一种融合天牛须搜索的教与学优化算法(TLBO algorithm with improved Beetle Antennae Search, BASTLBO)。首先利用Tent映射反向学习生成初始种群,在“教”阶段用天牛须算法优化调整教师个体的各维度,提升教师个体的状态;在“学”阶段,通过一种混合变异机制,提升学生个体逃离局部最优约束的能力。黎延海等[13]提出了一种随机交叉-自学策略改进的教与学优化算法(TLBO algorithm on random Crossover-self-study Strategy, CSTLBO),以学生可以自主随机选择交流学习的对象为出发点,在种群内随机选择当前个体的交流学习对象进行交叉学习,并对当前个体的部分较差的维度实施自我学习调整。王培崇[14]和李丽荣等[15]均在学习过程中引入参数,动态调整当前个体在“教”算子中自身状态的延续能力,并通过引入教师个体的动态搜索,勘探最优个体所在区域。
上述改进机制分别从个体变异、自学习和融合其他群体智能算法的搜索策略等角度提升算法性能,但均没有考虑粒子之间的竞争关系等。在一个教学班级中,同学之间必然是既有协作,亦存在竞争关系。本文提出了一种自适应竞争学习教与学优化算法(Improved TLBO algorithm with Adaptive Competitive learning, ITLBOAC)。通过引入近邻个体协作演化“学”算子,使近邻个体之间能够在早期协作进化、共同进步,并逐渐过渡到后期的竞争学习。既保证了算法的收敛速度,也使个体在迭代后期具有突跳变异能力。同时在“教”算子中引入自适应权值,动态调整当前个体在迭代过程中的自身状态保持和向教师学习的能力。
1 自适应竞争学习教与学优化算法
1.1 标准教与学优化算法
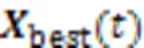
1.2 算法的改进描述
1.2.1自适应学习的“教”
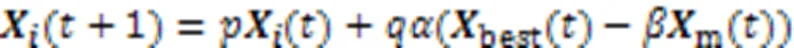
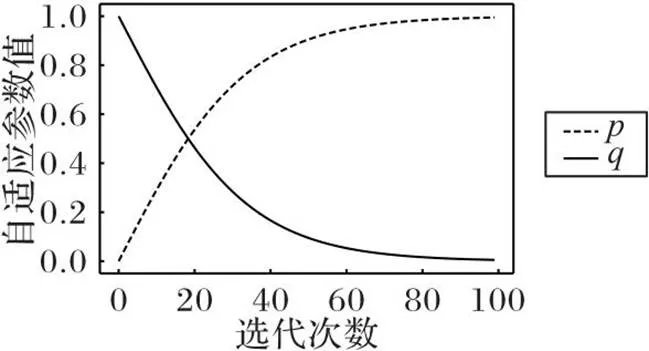
图1 参数p、q随迭代次数的变化
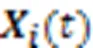
1.2.2近邻个体间协同演化的“学”
标准TLBO算法中的“学”赋予当前个体向种群内某随机个体进行学习的能力。它的主旨是赋予算法变异,避免因为“教”算子的引导,使种群过早收敛;但是,该算子在早期会减慢算法的收敛,而在后期由于种群的聚集,也很难取得最佳的变异效果,在多峰函数上的表现尤甚。
TLBO算法来自对班级学习行为的模拟。可视班级为一社会,即一个生态种群,种群内个体间必然存在协同演化行为,在演化过程中某些个体向优秀进化,而部分劣质个体因为竞争失败导致状态退化。在某真实的班级中,学生个体通常选择与自己状态相近的个体进行协同或者竞争,对于离自己较远(即状态相差较大)的个体很少直接发生关系。基于此,将标准“学”算子改造成一种近邻个体之间既能协作进化,同时又可以竞争的学习机制,称之为协同演化。
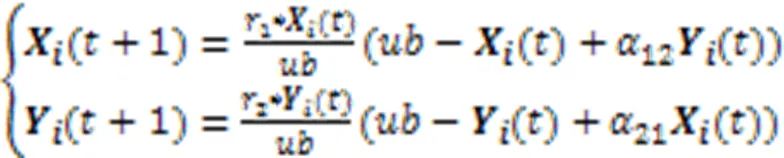

表1 Benchmark测试函数
分析新“学”算子可知,种群内的个体在进化早期,因为是协作进化的关系,参与的两个体之间互相学习和进步,不断提升自身的状态;同时,因为它们是近邻,状态较接近,而在协作进化中并没有其他个体的参与,所以这种协作进化的速度并没有特别快,有效缓冲了“教”算子的快速引导,避免过早地聚集于最优个体的周围。在后期,个体之间变成了竞争关系,会促使优秀的个体更加强大,协助最优个体进行勘探;而劣质个体因为竞争能力差,反而能够逃离当前区域的约束,去搜索其他的空间。
1.3 算法描述
算法1 自适应竞争学习教与学优化(ITLBOAC)算法。
输入 种群规模、维度、最大迭代次数等相关参数;
步骤1 在解空间内随机初始化种群。
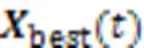
步骤3 种群内全部个体执行式(1),并采用贪婪机制更新自身状态。
步骤4 如果迭代次数在前1/3内,则种群内全部个体执行协同进化的“学”算子;否则,执行竞争行为的“学”算子(参见式(2))。
由于改进算法中并没有引入更为复杂的机制,所以该算法复杂度仍为(),与标准TLBO算法一致。
2 仿真实验与结果分析
2.1 测试函数及实验设置
为了验证算法的性能,基于Python编程实现ITLBOAC,测试环境选择笔记本电脑(CPU:AMD R7 4800U;内存:16 GB)。选择表1所列的12个benchmark测试函数测试算法的性能。
选择PSO(Particle Swarm Optimization)[17]、TLBO[1]、ITLBO[6]、CPTLBO[11]、BASTLBO[12]和DSLTLBO[15]作为对比算法。所有算法的种群规模均设为30,迭代次数设为100,其他参数均参考各自文献中的设置。求解问题的维度设为10或30。为了消除其他因素的影响,参与对比测试的算法均独立运行30次,计算30次运行结果的最优值、平均值以及标准差。表2为当=10时的测试结果,=30的测试结果列于表3。
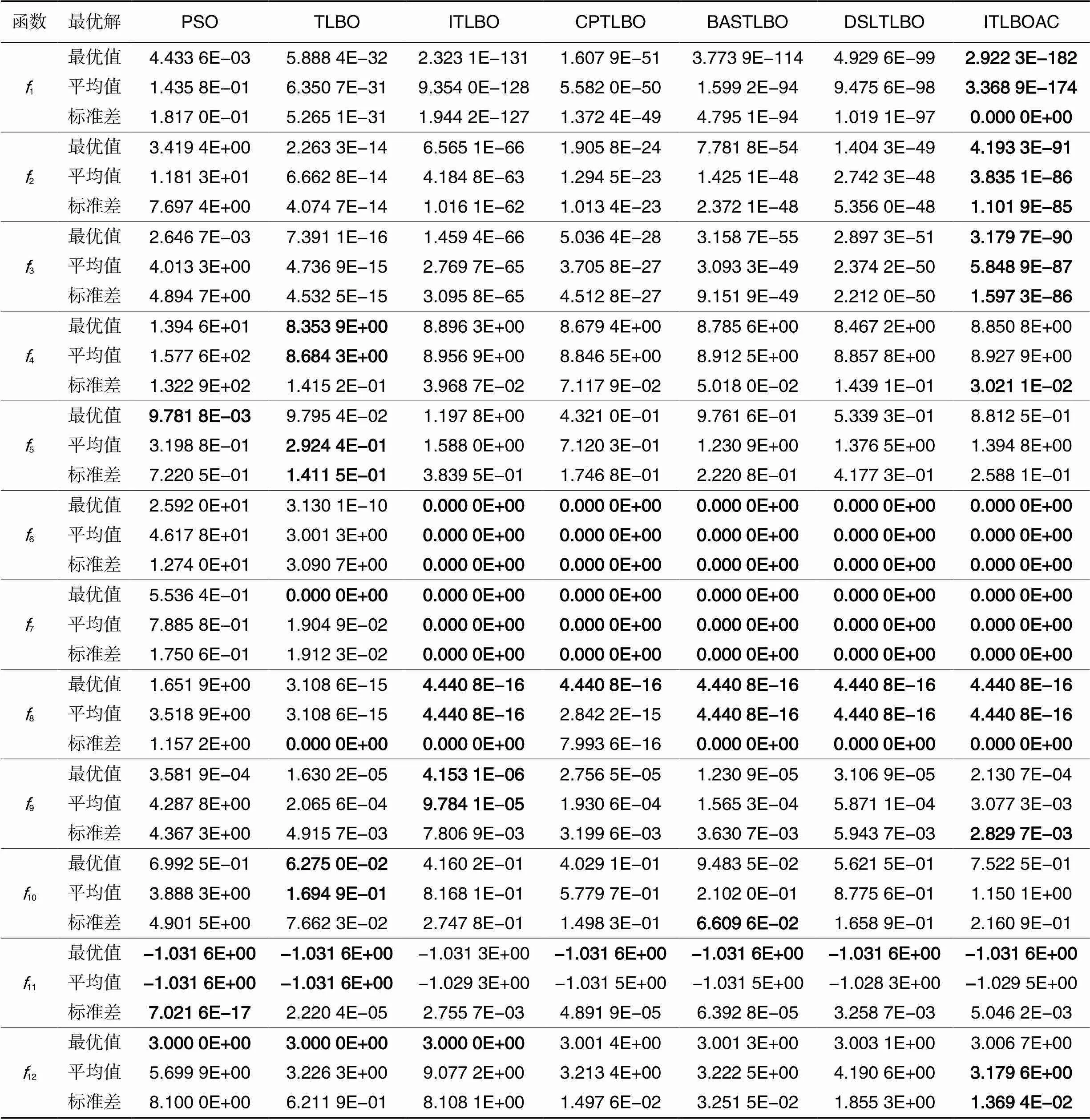
表2 10维下各算法的寻优结果
2.2 对比算法寻优结果及分析
分析表2可以看出,当=10时,ITLBOAC在其中的7个测试函数上获得了最佳最优值,在7个测试函数上获得了最佳平均值,在9个测试函数上获得了最佳标准差,表现出了良好的性能。对于123这3个函数,ITLBOAC的平均值分别低于TLBO算法近140、70、70个数量级,ITLBOAC表现出了出色的寻优能力;在45函数上,TLBO在所有算法中表现最佳,ITLBOAC虽然表现一般,但是它的标准差小,说明稳定性较好;在67函数上,5个改进算法的均值和稳定性一致,较TLBO和PSO性能大幅提升;8函数的测试结果表明,BASTLBO、ITLBOAC、ITLBO和DSLTLBO改进算法优势明显,而标准的TLBO和PSO则逊色很多;在9函数上,ITLBO的最优解和平均值均最好,而ITLBOAC的平均值和最优解与它有一定的差距,但标准差是全部算法中最好的;在10函数上,TLBO和BASTLBO的最优值和标准差均占优,ITLBOAC的平均值在7个算法中表现最差;在函数11上,参与对比的7个算法的最优值、平均值均为一个数量级,彼此没有差距,只是在稳定性上PSO算法最好,TLBO、CPTLBO和BASTLBO这3个算法次之。观察函数12上的表现,ITLBOAC、BASTLBO、CPTLBO3个算法的稳定性要优于其他的算法。
当问题维度增加到30时,更考验算法的搜索能力。分析表3的数据,可知PSO、TLBO两个算法性能下降较多;而其他5个改进算法的性能则下降较少。ITLBOAC在其中的7个测试函数上找到了最优值,在7个测试函数上获得了最佳平均值,在其中10个测试函数上的标准差为最佳,其他的测试函数上也与对比算法相当。综合上述的分析,可知ITLBOAC无论是高维度还是低维度,均表现出了较好的性能。
表330维下各算法的寻优结果
2.3 算法收敛速度对比
为了更为直观地比较各算法的收敛速度,图2列举了部分算法在维度为10时的收敛曲线。由图2可知,ITLBOAC在12个测试函数上具有更高的收敛速度。在123函数上,ITLBOAC的收敛快,收敛精度高,与其他对比算法有不同程度的差距;在4函数上,ITLBOAC曲线明显快于其他算法;在5函数上,改进算法都较快地完成收敛;在67测试函数上,ITLBOAC和BASTLBO在迭代前期下降曲线接近重合,但最终ITLBOAC在16次左右收敛到理论最优值0,略快于BASTLBO;在8测试函数上,ITLBOAC在25代左右趋于收敛,具有更高的收敛速度;910函数收敛曲线大致相同,ITLBOAC能够以较快的速度收敛到最优解周围,然后进行精细搜索;11函数上各算法收敛曲线大致重合;12函数上各算法收敛趋势大致相同,ITLBOAC的收敛速度也较高。综上所述,12个测试函数上,ITLBOAC均只需要较少的迭代次数,就能够快速收敛到最优值附近,然后进行精细勘探,说明该算法中引入的自适应学习以及协作演化与竞争策略,能够较好地平衡种群的开发和勘探,改进思路有效。
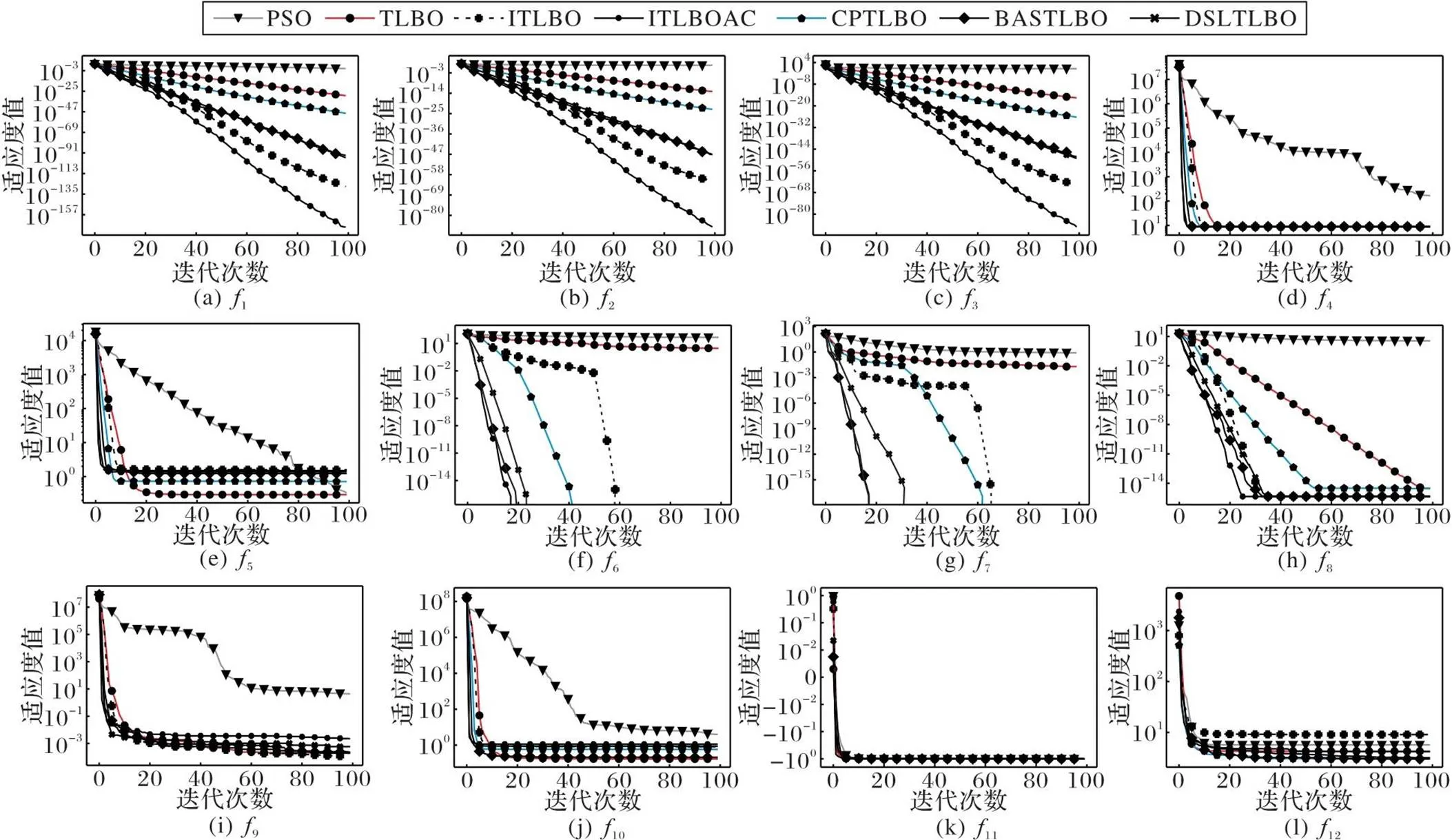
图2 10维下各算法的收敛曲线
3 约束工程优化问题中的应用
3.1 压缩弹簧优化设计问题
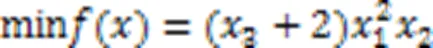
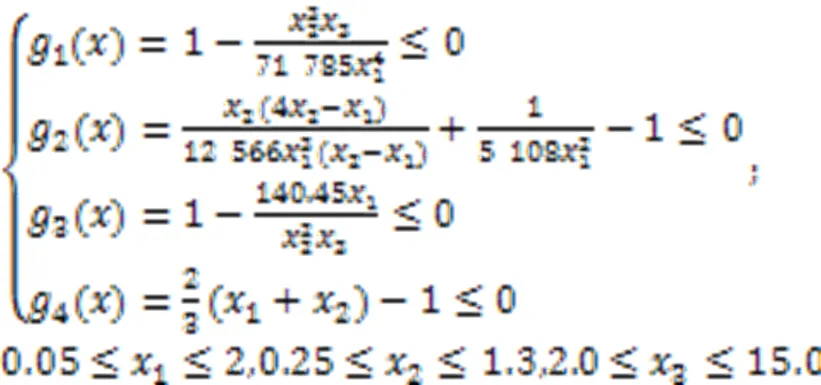
对于包含不等式约束的优化问题,本文采用罚函数方法[19]将它转化为求解无约束最优化问题。表4列出了TLBO、ITLBOAC等算法求解压缩弹簧优化设计问题所得到的最优重量和相关参数解。
表4压缩弹簧优化设计问题的寻优结果
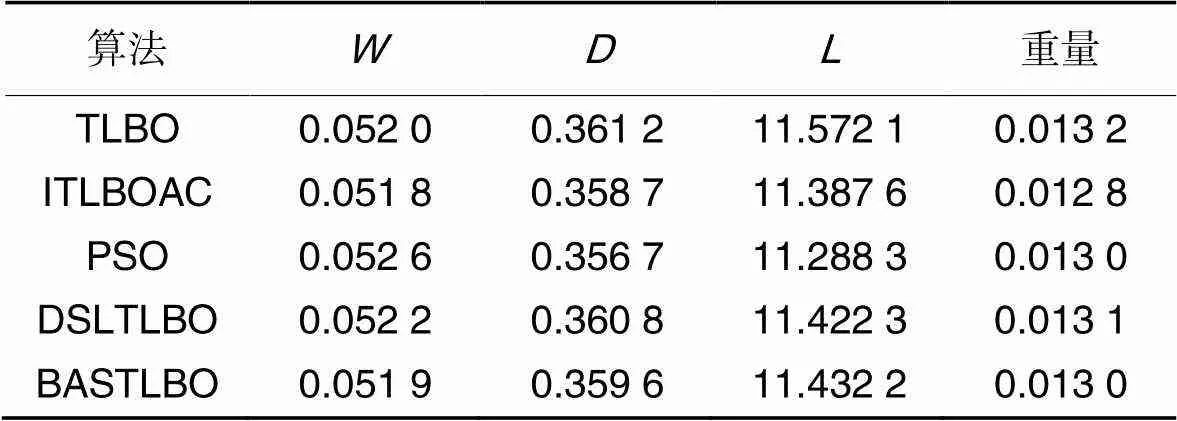
Tab.4 Optimization results for compression spring optimized design problem
由表4的数据可知,ITLBOAC设计的压缩弹簧重量在5个算法中最轻。与TLBO相比,ITLBOAC得到的弹簧重量降低了3.03%,线圈直径和簧圈直径也分别减小了0.38%、0.69%。说明对于复杂程度一般的压缩弹簧优化设计问题,ITLBOAC具有良好的性能。
3.2 三杆桁架优化设计问题
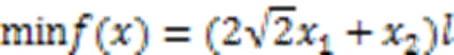
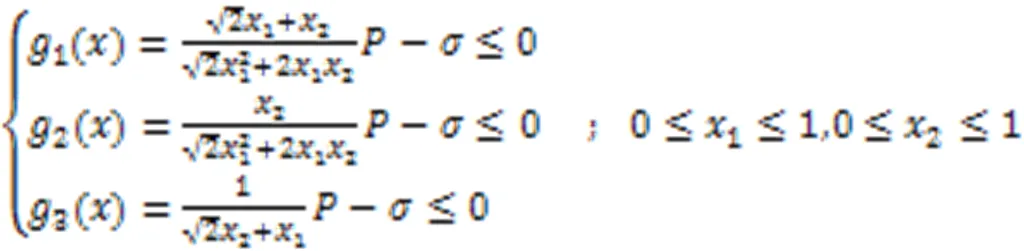
本文实验亦采用罚函数方法求解。表5列出了通过TLBO、ITLBOAC等算法求解三杆桁架优化设计问题时得到的最优体积及其对应解。
表5三杆桁架设计优化问题的寻优结果
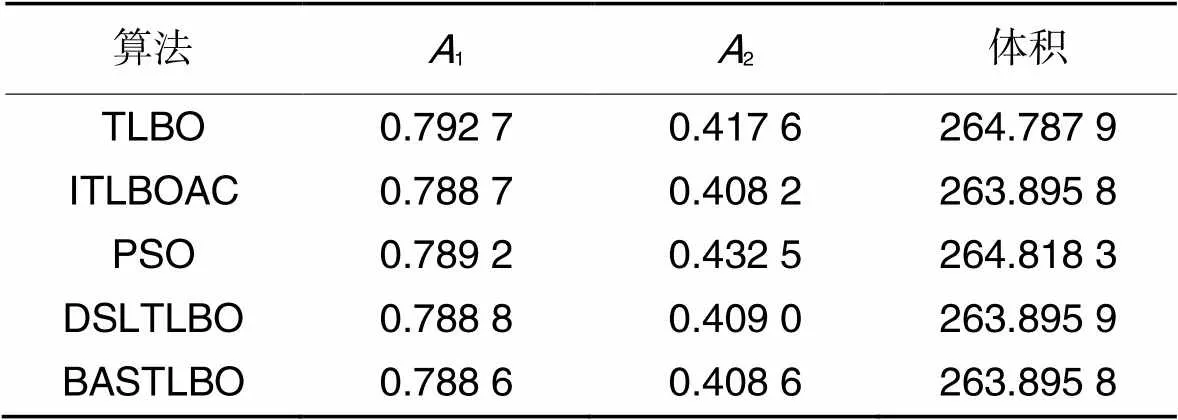
Tab.5 Optimization Results for three-bar truss optimized design problem
通过表5可知在三杆桁架优化问题中,ITLBOAC计算得到的三杆桁架的体积在5种算法中是最小的,1、2两个截面值也非常优秀。ITLBOAC得到的体积值较TLBO下降了0.34%,求解能力提升明显。
4 结语
本文提出了一种具有自适应竞争学习机制的改进TLBO算法,以克服该算法在求解较高维度问题时的弱点。新算法主要在以下两个方面引入了新策略:1)在“教”算子中引入了两个自适应权值,通过动态调整当前个体对教师的学习策略,以及自身状态保持的能力,平衡算法的全局和局部搜索能力;2)将标准“学”算子彻底改造成近邻个体之间的协同演化学习策略。仿真实验结果表明,所提算法在连续优化问题上表现了良好的性能,解精度较高、收敛快且稳定性优。最后将本文算法用于求解压缩弹簧和三杆桁架这两种典型的工程优化设计问题,实验结果表明本文算法在求解工程优化设计问题上也具有较好的求解质量和有效性。由于TLBO算法缺乏数学理论的支撑,未来将针对该算法的收敛性能进行分析,探索新的应用领域,结合传统的演化算法思想提升TLBO的性能。
[1] RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems [J]. Computer-Aided Design, 2011, 43(3):303-315.
[2] 曹劲松,熊福力. 基于离散教与学算法的分布式预制流水车间调度研究[J]. 计算机测量与控制, 2021, 29(12): 166-171, 183.(CAO J S, XIONG F L. Research on distributed precast flow shop scheduling based on discrete teaching-learning based optimization[J]. Computer Measurement and Control, 2021, 29(12):166-171, 183.)
[3] 左智科,李一龙. 改进的TLBO及其在自来水供水量预测中的应用[J]. 人民黄河, 2021, 43(2):84-87.(ZUO Z K, LI Y L. Improved TLBO and its application in tap water supply prediction[J]. Yellow River, 2021, 43(2):84-87.)
[4] 宋强. 基于群体智能优化算法的多行程车辆路径问题的研究[D]. 武汉:武汉理工大学, 2018:57-75.(SONG Q. Research of multi-trip vehicle routing problem based on swarm intelligence optimization algorithm[D]. Wuhan: Wuhan University of Technology, 2018:57-75.)
[5] 孙希霞,白晓东,许斌,等. 基于协同进化教与学优化算法的图像分割[J]. 南京邮电大学学报(自然科学版), 2019, 39(2):84-90.(SUN X X, BAI X D, XU B, et al. Co-evolutionary teaching-and-learning optimization algorithm based image segmentation[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science Edition), 2019, 39(2):84-90.)
[6] CHEN D, ZOU F, LI Z, et al. An improved teaching-learning-based optimization algorithm for solving global optimization problem[J]. Information Sciences, 2015, 297:171-190.
[7] ZOU F, WANG L, HEI X, et al. Teaching-learning-based optimization with dynamic group strategy for global optimization [J]. Information Sciences, 2014, 273:112-131.
[8] LI S, GONG W, WANG L, et al. A hybrid adaptive teaching-learning-based optimization and differential evolution for parameter identification of photovoltaic models[J]. Energy Conversion and Management, 2020, 225: No.113474.
[9] 高昊,张庆科,卜降龙,等. 基于协同变异与莱维飞行策略的教与学优化算法及其应用[J]. 计算机应用, 2023, 43(5):1355-1364.(GAO H, ZHANG Q K, BU X L, et al. Teaching-learning optimization algorithm based on collaborative variation and Lévy flight strategy and its application[J]. Journal of Computer Applications, 2023, 43(5):1355-1364.)
[10] 翟志波,贾国平,王涛,等.基于拉普拉斯分布与鲍德温效应的教与学算法及其应用[J]. 计算机集成制造系统, 2023, 29(8):2611-2621.(ZHAI Z B, JIA G P, WANG T, et al. Teaching and learning algorithm based on Laplace distribution and Baldwin effect and its application[J]. Computer Integrated Manufacturing Systems, 2023, 29(8):2611-2621.)
[11] 何佩苑,刘勇. 融合认知心理学理论的新型教与学优化算法及应用[J]. 计算机应用研究, 2022, 39(3):785-789, 796.(HE P Y, LIU Y. New teaching-learning-based optimization algorithm with cognitive psychology theory and its application[J]. Application Research of Computers, 2022, 39(3): 785-789, 796.)
[12] 欧阳城添,周凯. 融合改进天牛须搜索的教与学优化算法[J]. 计算机工程与应用, 2022, 58(4): 91-99.(OUYANG C T, ZHOU K. Teaching-learning based optimization algorithm with improved beetle antennae search[J]. Computer Engineering and Applications, 2022, 58(4): 91-99.)
[13] 黎延海,雍龙泉,拓守恒.随机交叉-自学策略改进的教与学优化算法[J]. 智能系统学报, 2021, 16(2):313-322.(LI Y H, YONG L Q, TUO S H. Teaching-learning-based optimization algorithm based on random crossover-self-learning strategy[J]. CAAI Transactions on Intelligent Systems, 2021, 16(2): 313-322.)
[14] 王培崇. 改进的动态自适应学习教与学优化算法[J]. 计算机应用, 2016, 36(3):708-712, 725.(WANG P C. Improved dynamic self-adaptive teaching-learning-based optimization algorithm[J]. Journal of Computer Applications, 2016, 36(3):708-712, 725.)
[15] 李丽荣,李木子,李崔灿,等.具有自适应动态学习机制的教与学优化算法[J]. 计算机工程与应用, 2020, 56(19):62-67.(LI L R, LI M Z, LI C C, et al. Teaching and learning based optimization with dynamic self-adaptive learning[J]. Computer Engineering and Applications, 2020, 56(19):62-67.)
[16] 曹先彬,罗文坚,王煦法.基于生态种群竞争模型的协同进化[J]. 软件学报, 2001, 12(4):556-562.(CAO X B, LUO W J, WANG X F.A co-evolution pattern based on ecological population competition model[J]. Journal of Software, 2001, 12(4):556-562.)
[17] KENNEDY J, EBERHART R C. Particle swarm optimization[C]// Proceedings of the 1995 International Conference on Neural Networks — Volume 4. Piscataway: IEEE, 1995: 1942-1948.
[18] 汪逸晖,高亮. 乌鸦搜索算法的改进及其在工程约束优化问题中的应用[J]. 计算机集成制造系统, 2021, 27(7):1871-1883.(WANG Y H, GAO L. Improvement of crow search algorithm and its application in engineering constrained optimization problems[J]. Computer Integrated Manufacturing Systems, 2021, 27(7): 1871-1883.)
[19] 刘景森,袁蒙蒙,李煜.基于改进樽海鞘群算法求解工程优化设计问题[J]. 系统仿真学报, 2021, 33(4):854-866.(LIU J S, YUAN M M, LI Y. Solving engineering optimization design problem based on improved salp swarm algorithm[J]. Journal of System Simulation, 2021, 33(4): 854-866.)
Improved TLBO algorithm with adaptive competitive learning
WANG Peichong1, FENG Haojing1, LI Lirong2*
(1,,050031,;2,,050031,)
For that the Teaching-Learning-Based Optimization (TLBO) algorithm has some problems, such as prematurity and poor solution accuracy, in solving high-dimensional optimization problems, an Improved TLBO algorithm with Adaptive Competitive learning (ITLBOAC) was proposed. Firstly, a weighted parameter with nonlinear change was introduced into the “teaching” operator to determine the ability of the current individual to maintain its own state and adjust the attitude of the current individual towards learning from teachers. As a result, the current individual learnt more from the teacher in the early stage to improve its own state quickly, and kept the state of itself more in the later stage to slow down the influence of the teacher on it. Then, based on ecological cooperation and competition mechanisms, a “learning” operator based on adaptive competition between nearest neighbor individuals was introduced. To make the current individual chose its near neighbors and the individuals eventually shifted from cooperative evolution to competitive learning. Test results on 12 Benchmark test functions show that compared with four improved TLBO algorithms, the proposed algorithm is better in terms of accuracy of solutions, stability and convergence speed, and is much better than TLBO algorithm at the same time, which verify that the proposed algorithm is suitable for solving high-dimensional continuous optimization problems. Test results with compression spring and three-bar truss design problems selected to test show that the optimal values obtained by ITLBOAC decreased by 3.03% and 0.34% respectively, compared with those obtained by TLBO algorithm. It can be seen that ITLBOAC is a trustworthy algorithm in solving constrained engineering optimization problems.
Teaching-Learning-Based Optimization (TLBO); adaptive learning; competitive learning; Lotka-Volterra model; constrained engineering optimization problem
This work is partially supported by Hebei Social Science Foundation (HB21GL050), Hebei Science and Technology Research Project for Higher Education Institutions (ZD2020344).
WANG Peichong, born in 1972, Ph. D., professor. His research interests include swarm intelligence, computer vision.
FENG Haojing, born in 1997, M. S. candidate. Her research interests include swarm intelligence, computer vision.
LI Lirong, born in 1973, M. S., assistant research fellow. Her research interests include intelligent decision-making.
A
1001-9081(2023)12-3868-07
10.11772/j.issn.1001-9081.2023010025
2023⁃01⁃11;
2023⁃04⁃30;
2023⁃05⁃15。
河北省社会科学基金资助项目(HB21GL050);河北省高等学校科学技术研究项目(ZD2020344)。
王培崇(1972—),男,河北辛集人,教授,博士,CCF会员,主要研究方向:群体智能、计算机视觉;冯浩婧(1997—),女,河北唐山人,硕士研究生,CCF会员,主要研究方向:群体智能、计算机视觉;李丽荣(1973—),女,河北张家口人,助理研究员,硕士,主要研究方向:智能决策。

