带状稀疏矩阵乘法及高效GPU实现
刘丽,陈长波*
带状稀疏矩阵乘法及高效GPU实现
刘丽1,2,陈长波1*
(1.中国科学院 重庆绿色智能技术研究院,重庆 400714; 2.中国科学院大学 重庆学院,重庆 400714)(∗通信作者电子邮箱chenchangbo@cigit.ac.cn)
稀疏-稠密矩阵乘法(SpMM)广泛应用于科学计算和深度学习等领域,提高它的效率具有重要意义。针对具有带状特征的一类稀疏矩阵,提出一种新的存储格式BRCV(Banded Row Column Value)以及基于此格式的SpMM算法和高效图形处理单元(GPU)实现。由于每个稀疏带可以包含多个稀疏块,所提格式可看成块稀疏矩阵格式的推广。相较于常用的CSR(Compressed Sparse Row)格式,BRCV格式通过避免稀疏带中列下标的冗余存储显著降低存储复杂度;同时,基于BRCV格式的SpMM的GPU实现通过同时复用稀疏和稠密矩阵的行更高效地利用GPU的共享内存,提升SpMM算法的计算效率。在两种不同GPU平台上针对随机生成的带状稀疏矩阵的实验结果显示,BRCV的性能不仅优于cuBLAS(CUDA Basic Linear Algebra Subroutines),也优于基于CSR和块稀疏两种不同格式的cuSPARSE。其中,相较于基于CSR格式的cuSPARSE,BRCV的最高加速比分别为6.20和4.77。此外,将新的实现应用于图神经网络(GNN)中的SpMM算子的加速。在实际应用数据集上的测试结果表明,BRCV的性能优于cuBLAS和基于CSR格式的cuSPARSE,且在大多数情况下优于基于块稀疏格式的cuSPARSE。其中,相较于基于CSR格式的cuSPARSE,BRCV的最高加速比为4.47。以上结果表明BRCV可以有效提升SpMM的效率。
带状稀疏矩阵;稀疏存储格式;稀疏矩阵乘法;图形处理单元;共享内存
0 引言
稀疏矩阵是元素大部分为零的矩阵,它的非零元素占比非常小,通常小于总数的1%。稀疏矩阵乘法广泛应用于大型科学计算[1]、深度学习[2-6]、分子化学[7]和图形分析计算[8-10]等领域。特别在深度学习领域,利用矩阵的稀疏性已成为提高深度神经网络训练和推理性能,以及在保持准确性的同时减小模型大小的主要方法之一[2,11-13]。在图神经网络(Graph Neural Network, GNN)[4]中,表示图的邻接矩阵通常具有稀疏性,稀疏-稠密矩阵乘法(Sparse-dense Matrix Multiplication, SpMM)因此成为GNN训练和推理中的主要操作之一[8-9,14]。
稀疏矩阵的存储格式很多,其中以下4种基本的存储格式被广泛接受:行压缩(Compressed Sparse Row, CSR)格式、坐标格式(COOrdinate format, COO)、ELLPACK(ELL)和对角线格式(DIAgonal format, DIA)[15-16]。此外,Liu等[17]提出了基于CSR扩展的CSR5格式;Ecker等[18]针对3种不同的并行处理器架构提出了CSR5BC(CSR5 Bit Compressed)、HCSS(Hybrid Compressed Slice Storage)和LGCSR(Local Group CSR)这3种新的稀疏矩阵格式,均分别在相应的目标架构上提供了良好的性能;Xie等[19]提出了CVR(Compressed Vectorization-oriented sparse Row)格式,可以同时处理输入矩阵中的多个行以提高缓存效率;程凯等[20]提出了由ELL和CSR格式混合而成的HEC(Hybrid ELL and CSR)格式,改善稀疏矩阵的存储效率;Zhang等[21]提出了两种适用于ARM处理器的对齐存储格式ACSR(Aligned CSR)和AELL(Aligned ELL),实验结果证明了这两种格式均具有明显的性能优势;Coronado-Barrientos等[22]提出了适用于不同体系结构的AXT格式,实验结果表明它可提高不同稀疏模式矩阵的存储效率;Bian等[23]提出了单一格式CSR2,实验表明该格式可实现低开销的格式转换和高吞吐量的计算性能,与CSR5相比,性能有明显提升;Karimi等[24]提出了一种平衡线程级并行和内存效率优化的图形处理单元(Graphics Processing Unit,GPU)内存感知格式VCSR(Vertical CSR),通过设计可配置的重排序方案可以最小化转换开销,显著减少全局内存事务的数量。
很多学者针对特殊稀疏结构提出特殊格式,特别是针对分块稀疏的研究工作有很多,其中应用最广泛的是块压缩稀疏行(Blocked Compressed Sparse Row, BCSR)格式以及基于此的一些变体。由于BCSR格式对整个矩阵使用单一的分块划分大小,并且要求分块严格对齐,因此会显式地引入更多的零填充。Vuduc等[25]提出了不对齐的BCSR(Unaligned BCSR, UBCSR)和可变块行(Variable Block Row, VBR)格式,以存储不同分块大小的子矩阵;Almasri等[26]提出了一种稀疏矩阵压缩块存储格式CCF(Compressed Chunk storage Format),将非零元数相同的行分配给同一个块,以增强负载平衡,在Intel x86处理器上的实验结果表明它为非结构化矩阵提供了优异的性能;杨世伟等[27]提出了基于BRC格式改进的BRCP(Blocked Row-Column Plus)存储格式,这种格式采用二维分块的方法,针对稀疏矩阵非零元分布特点,自适应地选择分块参数,保证了BRC格式的高效运行,优化了计算结果的确定性,且确保了再现性,具有较高的效率;Li等[28]提出了VBSF(Variable Blocked SIMD Format)格式,解决了主存访问的不连续性的问题,提高了存储和计算效率;Ahrens等[29]提出一种快速优化的VBR矩阵行划分算法1D-VBR(1D-Variable Block Row),在固定列分组的条件下确定最佳的行分组划分方式;Aliaga等[30]提出一种基于坐标稀疏矩阵格式的变体,将稀疏矩阵的非零元划分为相等大小的块以分配工作负载,该格式平衡了工作负载并压缩了索引数组和数值信息,适用于多种多核处理器平台。
由于稀疏矩阵乘法的重要性,很多学者基于上述稀疏格式,特别是CSR格式,在CPU、GPU、FPGA(Field-Programmable Gate Array)等不同硬件平台上对稀疏矩阵的效率进行改进,特别地,基于GPU的研究工作较多。NVIDIA 公司提供了一个cuSPARSE库[31]处理稀疏矩阵的乘法,在cuSPARSE库中,有一组基本线性代数子程序,用于处理稀疏矩阵。此外,Yang等[3]基于CSR格式,在GPU上实现了两种高效的SpMM算法,主要采取行划分和均匀分配非零值两种策略,以实现稠密矩阵的合并访问以及TLP(Thread-Level Parallelism)和ILP(Instruction-Level Parallelism)的负载平衡,实验结果表明该算法相较于cuSPARSE平均可实现2.69的加速比;Huang等[8]提出GE-SpMM(GEneral-purpose Sparse Matrix-matrix Multiplication),用于GNN在GPU上的应用,可以更高效地加载数据,减少总内存事务,并优于cuSPARSE库的SpMM算法;Wang等[11]提出了一种基于GPU用于SpMM算法的代码生成器SparseRT,直接生成PTX(Parallel Thread Execution)代码,加速了DNN(Deep Neural Network)的推理;Gale等[2]开发了基于CSR存储格式的专门针对深度学习应用的SpMM算法的GPU实现,可以降低内存需求,相较于cuSPARSE平均可达到3.58的加速比;但当问题规模较大时,算法的性能会受到共享内存带宽的限制。
本文针对一类稀疏矩阵提出一种新的存储格式BRCV(Banded Row Column Value)。这一类稀疏矩阵的特点是非零元素呈带状分布,即具有一致列下标的相邻行天然形成不同的带子,同一带子中非零元素的列下标可以不连续,即同一带子中的非零元素呈线状或块状分布;反之,位于相同行的所有块也可形成一个带子。因此带稀疏存储格式BRCV可看作分块稀疏格式,包括均匀分块稀疏格式BCSR及其变种可变分块格式UBCSR的一种推广。与这些分块格式不同,BRCV不需要对带子中的块单独标记和处理。带状稀疏矩阵广泛存在于和图相关的应用中,如现实世界中的图广泛存在社区结构[32-35],这种图的邻接矩阵就天然呈稀疏带状分布,且该带状不是传统的对角带状[36]。
本文的主要工作如下:
1)提出了带稀疏存储格式BRCV。与CSR格式相比,可以显著降低存储复杂度。
2)提出了基于BRCV格式的spMM算法以及高效的GPU实现。与已有的基于CSR格式的GPU实现相比,基于BRCV格式的GPU实现能同时对稀疏和稠密矩阵高效地利用GPU的共享内存。
3)提出了一种新的基于CSR格式的SpMM的高效GPU实现SCSR(Shared-memory CSR)。它采用了分块和针对稀疏矩阵的共享内存优化等技术,效率优于NVIDIA的cuSPARSE。
4)在随机生成的带状稀疏矩阵和GNN实际应用的数据集上对基于BRCV的SpMM实现的性能进行了评估。结果表明SpMM算法的GPU实现性能明显优于SCSR、cuBLAS(CUDA Basic Linear Algebra Subroutines)和基于CSR格式的cuSPARSE,多数情况下性能优于基于块稀疏格式的cuSPARSE,验证了BRCV格式的优势。
本文团队针对工作1)和2)已提交了一篇专利[37],并简单地报告了基于BRCV格式的稀疏稠密矩阵乘法的GPU性能。
1 背景知识
1.1 稀疏矩阵及存储格式
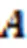
图1 稀疏矩阵
1.2 稀疏矩阵乘法
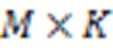
1.3 块稀疏格式
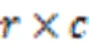
BCSR相较于CSR具有数据连续性的优势,且分块大小固定使得并行优化效率提升。但由于BCSR格式要求分块严格对齐,当矩阵维度不能整除分块大小时,需要填充整行或整列的零元;另一方面,BCSR格式在存储过程中将每个非零块看作稠密矩阵进行存储,因此会显式地引入更多零元素,尤其当非零元在稀疏矩阵中分布较为分散时,会带来较大的存储代价和性能损失。
图2显示了如何对图1中的矩阵以BCSR格式存储(分块大小为2×2)。实际计算中,分块大小的取值可以根据矩阵特征取最优值。
图2 BCSR格式
1.4 GPU及CUDA编程模型
GPU的系统架构是单指令多线程(Single Instruction Multiple Threads, SIMT)。一个GPU由多个流多处理器(Streaming Multiprocessor, SM)组成,一个SM由多个流处理器(Streaming Processor, SP)和一些其他的关键资源(寄存器、共享内存)组成。统一计算设备架构(Compute Unified Device Architecture, CUDA)提供了应用程序和GPU硬件之间的桥梁。在CUDA架构下,一个程序被划分为Host端和Device端两部分:Host 端指在CPU上执行的部分,Device 端指在GPU上执行的部分。CUDA中的核心概念是内核函数,内核函数从 CPU 端调用,运行在GPU上,一般把算法最耗时的部分放在内核函数中,利用GPU强大的计算能力快速完成。
在CUDA架构下,GPU执行时的最小单位是线程(Thread)。CUDA将线程组织成几个不同的层次:网格(Gird)、线程块(Thread Block)、线程束(Warp)和线程。几个线程可以组成一个线程块,几个线程块可以组成一个线程网格,线程块中的线程被组织成Warp的形式,每个周期、每个SM的硬件调度程序都会选择下一个要执行的Warp(即只有Warp被交换进出,而不是单独的线程),使用细粒度多线程同步隐藏内存访问延迟。在内核函数中,不同线程块之间彼此独立,不能相互通信,按照任意顺序串行或并行执行。每个线程有自己的寄存器空间,同一个线程块中的每个线程则可以共享一份共享内存,所有的线程都共享一份全局内存、常量内存和纹理内存。共享内存比寄存器慢,但是比全局内存快,因此适当使用共享内存和寄存器资源利用数据重用和局部性对性能至关重要。
1.5 GNN和图社区结构
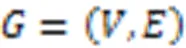
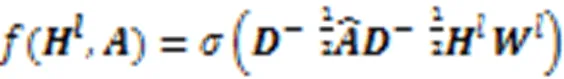
一个网络中的社区结构是指网络中的节点集合满足:1)同一社区的节点之间联系相对紧密;2)不同社区的节点之间联系相对稀疏的结构属性,这些节点组成的集合就是社区,一个简单的具有社区结构的网络如图3(a)所示,它的邻接矩阵见图3(b)。容易看出,邻接矩阵有4个带子,对于一般的具有社区结构性质的图,邻接矩阵也具有带状稀疏结构。
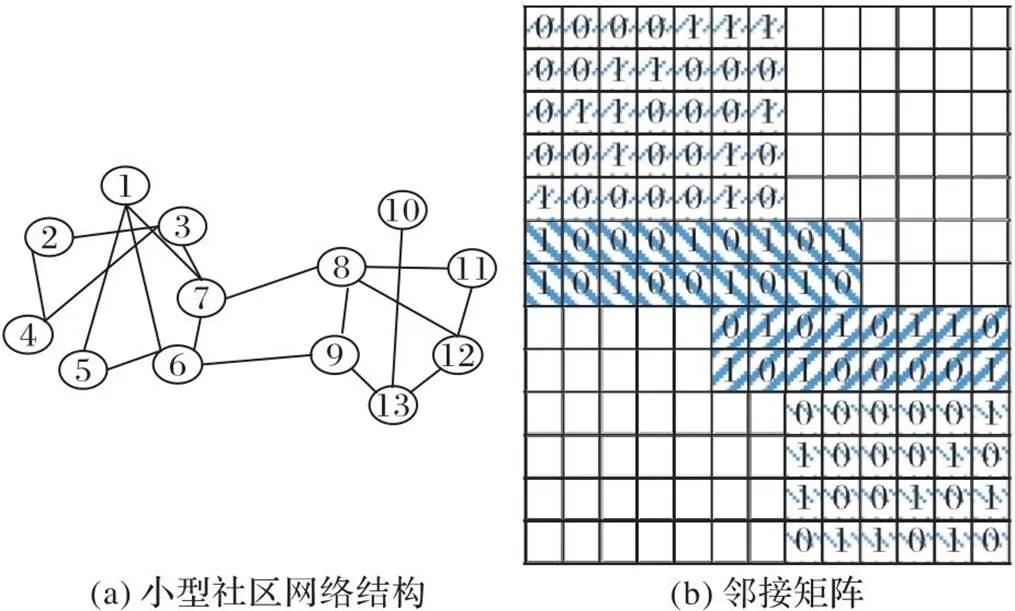
图3 社区结构网络
2 带稀疏矩阵存储格式
2.1 带稀疏矩阵概念
稀疏矩阵中有一种常见的具有局部性特征结构的矩阵:带稀疏矩阵,如图4所示。该类型的矩阵有若干稀疏带,同一个稀疏带里所有行的非零元列下标均相同,稀疏带内的行数称为该稀疏带的高度。
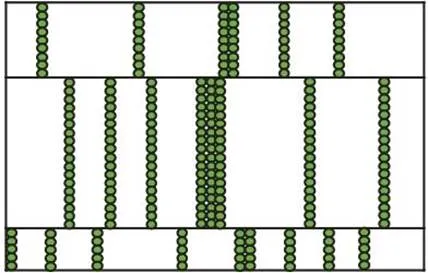
图4 带稀疏矩阵
2.2 带稀疏格式
针对带稀疏矩阵的性质,对CSR格式改进,提出了带稀疏矩阵的数据存储格式BRCV,以减小冗余的存储空间,有利于带稀疏矩阵乘法的高效GPU实现。
采用BRCV格式存储时可表示为:
因此,采用BRCV格式只需存储42个元素,而采用CSR格式需要存储63个元素,采用BCSR格式需要存储75个元素。显然,BRCV格式优于CSR和BCSR格式。其中,BCSR格式所需存储空间与分块大小有关,实验中根据平台特征和优化技术的不同,定义的分块大小也不同,在此例中即使采用更佳的分块大小5×1,BCSR格式仍需存储45个元素,存储复杂度高于BRCV格式。
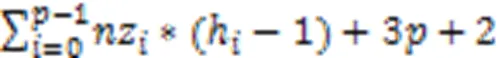
证明 BRCV格式的存储复杂度为:
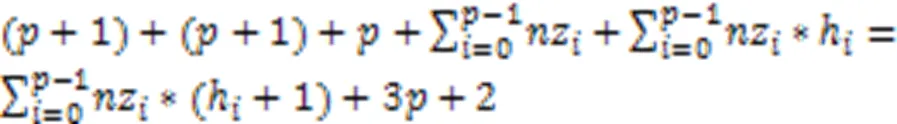
CSR格式的存储复杂度为:
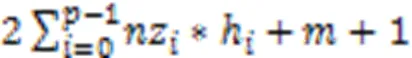
式(2)减去式(1)得到:
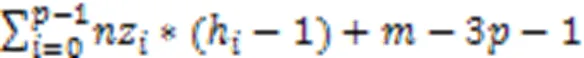
因此,当式(3)结果大于0时,CSR格式的存储复杂度高于BRCV格式的存储复杂度。
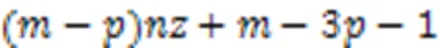
推论得证。
2.3 稀疏稠密矩阵乘法
本文给出一种基于BRCV格式的SpMM算法,见算法1。
算法1 基于BRCV格式的SpMM算法。
1) for=0 to-1 do
2) for=0 to-1 do
3)=[+1]-[]
4) for=0 to[+1]-[]-1 do
5)=0
6)=[] +
7) for=0 to-1 do
8)=[[]+]
9)+=[+]*[,]
10)[+[],]=
2.4 等高带稀疏矩阵乘法EBRCV
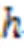
2.5 BRCV相对于CSR的优势
3 带稀疏矩阵GPU实现
3.1 基本思想
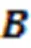
图5 基于BRCV格式的SpMM的GPU实现
3.2 具体实现
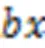
1)=blockIdx.,=blockIdx.
2)=threadIdx.,=threadIdx.
3)=*blockDim.+
4)=[],=[]
5)=[+1]–[]
6)=%= 0?:%
7)=*+
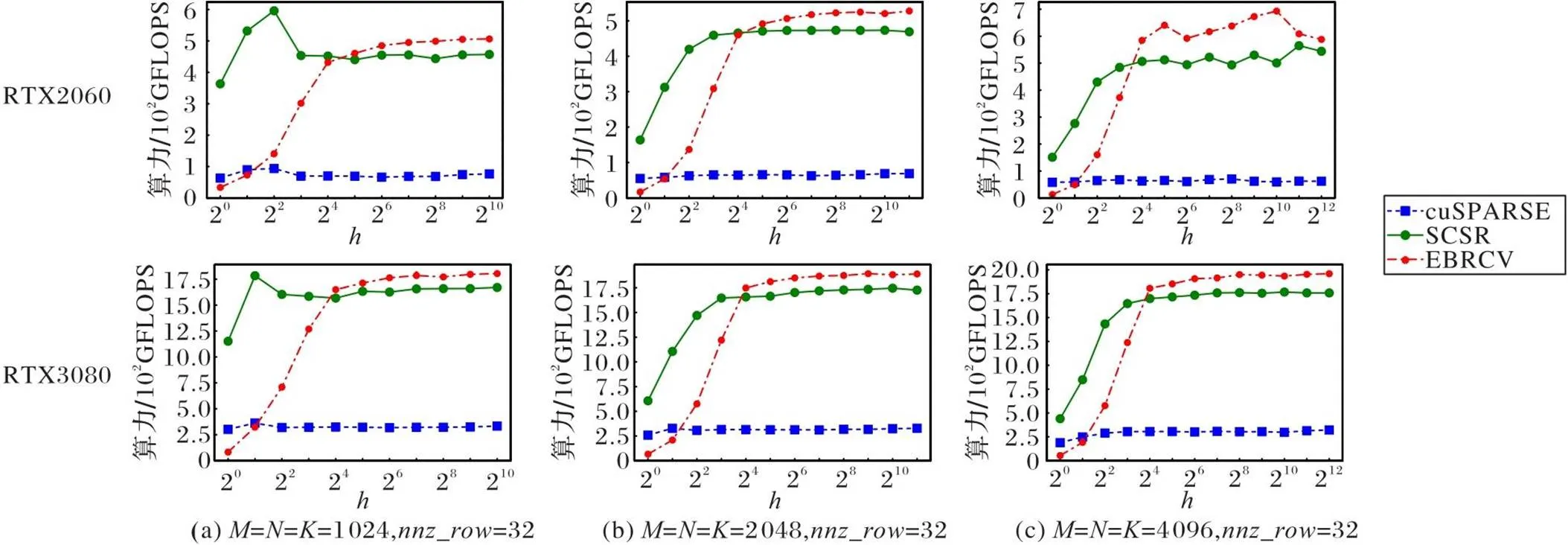
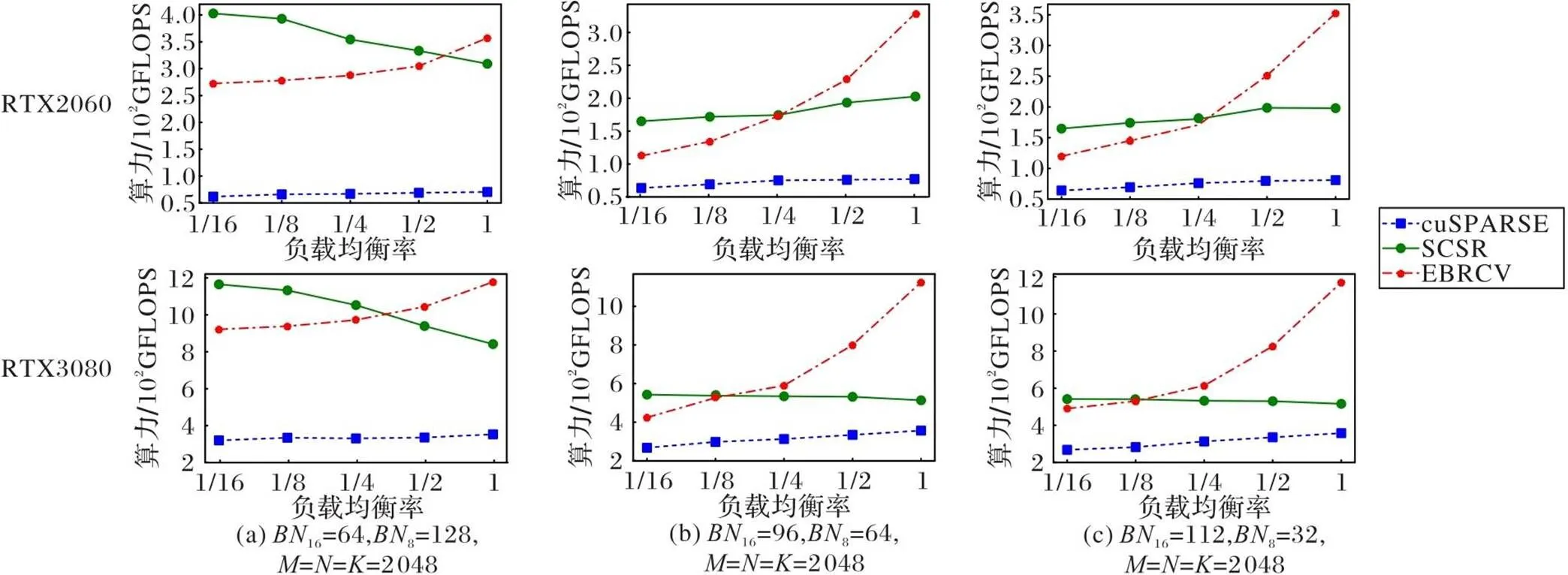
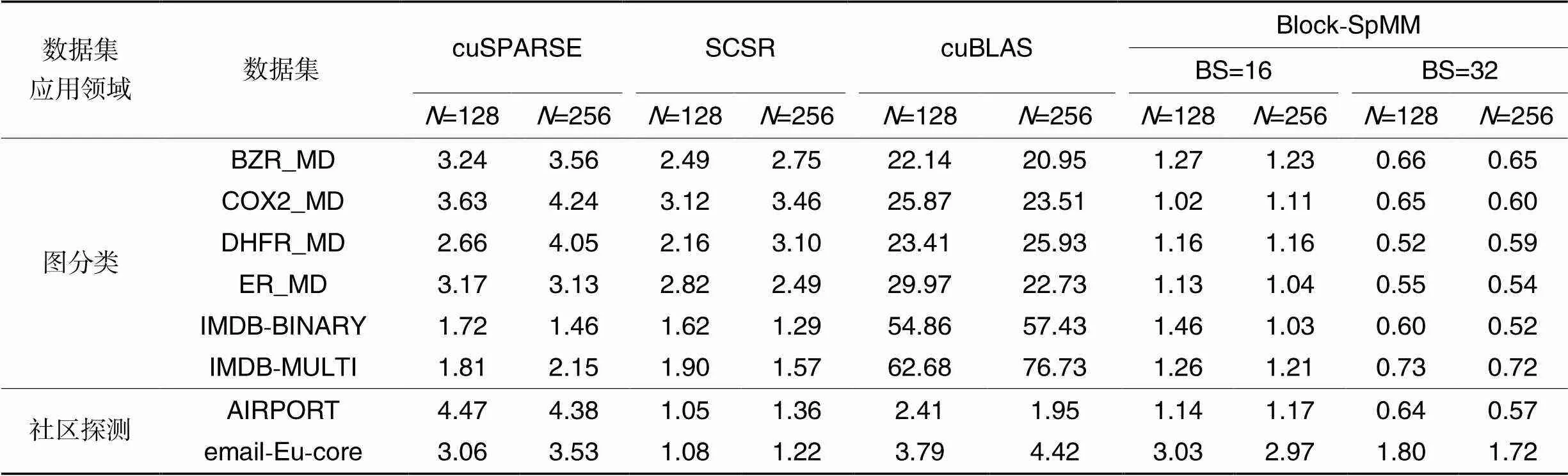
8) if 9)=[+1]–[] 10)=0 11)=[]+* 12) for=0 to-1 stepdo 13) /*apply for shared memory:[]、 [][]、[][]*/ /*load.col、.val with tile*/ 14) if+ 15)[]=[[]++] 16)[][]=[++] 17) __syncthreads() 18) /*loadwith tile×*/ 19) for=0 to-1 stepdo 20)=+ 21) if 22)=[] 23)[][]=[,] 24) __syncthreads() 25) /*consume the loaded elements*/ 26) for=0 to-1 do 27) if<-then 28)+=[][]*[][] 29) __syncthreads() 30)[[]+,] = 基准三为NVIDIA公司开发的一个高性能cuBLAS数值库,记为cuBLAS[39]。cuBLAS是标准基本线性代数子例程(Basic Linear Algebra Subroutine, BLAS)的CUDA实现,包含了高性能的矩阵乘法。 在以下两种不同的GPU平台上对随机生成的稀疏带状矩阵进行实验,实验更具有说服性,更能说明本文格式的优势。 1)CPU为Intel Core i9-9900 3.10 GHz,8核,16 GB内存,GPU为NVIDIA GeForce RTX 2060,CUDA Version:11.7。 2)CPU为11th Gen Intel Core i9-11900K CPU,3.50 GHz,8核,128 GB内存,显卡为NVIDIA GeForce RTX 3080,CUDA Version:11.6。 为了科学地评估SpMM的3种GPU实现的性能,选取了5类测试用例。 针对等高带稀疏矩阵: 例1 固定带高,考察每行非零元数变化时3种实现的性能差异。 例2 固定每行非零元数,考察稀疏带高度变化时3种实现的性能差异。 针对非等高的带稀疏矩阵: 例3 考察线程块的负载均衡率变化时3种实现的性能差异。 例4 令稀疏带的高度在不同范围内取值,以考察BRCV效率较高的稀疏带高度范围。 例5 稀疏带的高度与每行非零元数均随机,以考察一般情况下不同实现的性能差异。 此外,为了评估BRCV格式的SpMM的GPU实现在GNN应用中的性能,选取了两类用于不同图任务的数据集。 1)图分类任务。 选自不同领域内的6组数据集。生物化学领域:BZR_MD、COX2_MD、DHFR_MD和ER_MD;社交网络领域:IMDB-BINARY和IMDB-MULTI,这几组数据均可在TUDataset数据集[41]中找到(TUDataset是一组用于图形学习的基准数据集)。 以用于苯二氮卓受体的配体数据集BZR_MD为例,如表1所示,BZR_MD数据集由306个子图组成,每个子图对应一个邻接矩阵,每个邻接矩阵均可视为一个稀疏带,子图的节点数代表这个稀疏带的带高,则由这些子图拼接而成的大的稀疏矩阵自然地形成带状结构,数据集的总节点数代表稀疏矩阵的维度。其他数据集同理。 表1图分类数据集的详情 2)社区探测任务。 选自社交网络领域的两组数据集:AIRPORT[42]、email-Eu-core[43]。AIRPORT是一个直推式的数据集,其中节点表示机场,边表示连接机场间的航线,选取部分机场和航线数;email-Eu-core数据集节选自某个欧洲大型研究机构在18个月期间的电子邮件网络,给定一组电子邮件,每个节点对应一个电子邮件,如果存在两个节点双向交换消息,就在它们中间创建一个边。 对于这两组数据集,对选取的部分节点进行了重排,使它呈现更规则的带状稀疏分布,并且由于机场数据集AIRPORT和电子邮件数据集email-Eu-core的特殊性,在合理范围内增加了一些节点之间的边。AIRPORT数据集包含3188个节点,48441条边;email-Eu-core数据集包含1005个节点,28469条边。 针对随机生成的例1~4,本文综合考虑了每行非零元数、稀疏带高度和线程块的负载均衡等相关因素,对比实验基准一cuSPARSE和实验基准二SCSR,验证BRCV实现的适用范围和算法性能加速效果。针对随机生成的例5和GNN应用中的数据集,本文对比了4个实验基准:cuSPARSE、SCSR、cuBLAS和Block-SpMM,以考察一般情况下,以及GNN的算子加速中不同SpMM实现的性能差异。 图6 不同GPU上稀疏矩阵每行非零元数变化时,不同SpMM实现在例1上的性能 Fig. 6 Performance of different SpMM implementations for example 1 on different GPU when number of non-zero elements on each row of sparse matrix varies 图7 不同GPU上稀疏矩阵带高变化时,不同SpMM实现在例2上的性能 图8 不同GPU上线程块负载均衡率变化时,不同SpMM实现在例3上的性能 图9 不同GPU上非等高带稀疏矩阵带高变化时,不同SpMM实现在例4上的性能 图8、9表示非等高带稀疏矩阵在不同GPU平台上3种SpMM实现的实验结果。可以看出:随着线程块负载均衡率的增大,BRCV性能明显提升,并逐渐超过SCSR;随着非等高带稀疏矩阵最小带高的增大,BRCV的性能逐渐超过cuSPARSE和SCSR。性能提升的主要原因是:与SCSR和cuSPARSE这两种实现相比,BRCV实现对SpMM算法中的稀疏矩阵和稠密矩阵均使用了共享内存优化,实现了稠密矩阵的行复用,减少了数据传输时间,提高了计算效率。 表2不同GPU上非等高带稀疏矩阵带高和每行非零元数均变化时,不同SpMM实现的性能对比 Tab.2 Performance comparison of different SpMM implementations on different GPU when both band height and the number of non-zero elements on each row of non-equal height band sparse matrix vary 注:加粗表示最大值,下画线表示次优值,双下画线表示最差结果;最大、最小加速比表示本文算法与最差及次优结果的比值。 表3BRCV相较于其他4种SpMM在图分类和社区探测数据集上实现的加速比 Tab.3 Speedup ratios of BRCV compared to other four SpMM implementations on graph classification and community detection datasets [1] 刘伟峰. 高可扩展、高性能和高实用的稀疏矩阵计算研究进展与挑战[J]. 数值计算与计算机应用, 2020, 41(4): 259-281.(LIU W F. Highly-scalable, highly-performant and highly-practical sparse matrix computations: progress and challenges[J]. Journal of Numerical Computation and Computer Applications, 2020, 41(4): 259-281.) [2] GALE T, ZAHARIA M, YOUNG C, et al. Sparse GPU kernels for deep learning[C]// Proceedings of the 2020 International Conference for High Performance Computing, Networking, Storage and Analysis. Piscataway: IEEE, 2020: 1-14. [3] YANG C, BULUÇ A, OWENS J D. Design principles for sparse matrix multiplication on the GPU[C]// Proceedings of the 2018 European Conference on Parallel Processing, LNCS 11014. Cham: Springer, 2018: 672-687. [4] XU K, HU W, LESKOVEC J, et al. How powerful are graph neural networks?[EB/OL]. (2019-02-22)[2023-02-25].https://arxiv.org/pdf/1810.00826.pdf. [5] XIN J, YE X, ZHENG L, et al. Fast sparse deep neural network inference with flexible SpMM optimization space exploration[C]// Proceedings of the 2021 IEEE High Performance Extreme Computing Conference. Piscataway: IEEE, 2021: 1-7. [6] DAVE S, BAGHDADI R, NOWATZKI T, et al. Hardware acceleration of sparse and irregular tensor computations of ML models: a survey and insights [J]. Proceedings of the IEEE, 2021, 109(10): 1706-1752. [7] COLEY C W, JIN W, ROGERS L, et al. A graph-convolutional neural network model for the prediction of chemical reactivity[J]. Chemical Science, 2019, 10(2): 370-377. [8] HUANG G, DAI G, WANG Y, et al. GE-SpMM: general-purpose sparse matrix-matrix multiplication on GPUs for graph neural networks [C]// Proceedings of the 2020 International Conference for High Performance Computing, Networking,Storage and Analysis. Piscataway: IEEE, 2020: 1-12. [9] NAGASAKA Y, NUKADA A, KOJIMA R, et al. Batched sparse matrix multiplication for accelerating graph convolutional networks[C]// Proceedings of the 19th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing. Piscataway: IEEE, 2019: 231-240. [10] HOEFLER T, ALISTARH D, BEN-NUN T, et al. Sparsity in deep learning: pruning and growth for efficient inference and training in neural networks[J]. Journal of Machine Learning Research, 2021, 22: 1-124. [11] WANG Z. SparseRT: accelerating unstructured sparsity on GPUs for deep learning inference [C]// Proceedings of the 2020 ACM International Conference on Parallel Architectures and Compilation Techniques. New York: ACM, 2020: 31-42. [12] CHILD R, GRAY S, RADFORD A, et al. Generating long sequences with sparse Transformers[EB/OL]. (2019-04-23)[2023-02-25].https://arxiv.org/pdf/1904.10509.pdf. [13] KITAEV N, KAISER Ł, LEVSKAYA A. Reformer: the efficient Transformer [EB/OL]. (2020-02-18)[2023-02-25].https://arxiv.org/pdf/2001.04451.pdf. [14] YANG C, BULUÇ A, OWENS J D. GraphBLAST: a high-performance linear algebra-based graph framework on the GPU[J]. ACM Transactions on Mathematical Software, 2022, 48(1): 1-51. [15] LANGR D, TVRDÍK P. Evaluation criteria for sparse matrix storage formats [J]. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(2): 428-440. [16] CHOU S, KJOLSTAD F, AMARASINGHE S. Automatic generation of efficient sparse tensor format conversion routines[C]// Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation. New York: ACM, 2020: 823-838. [17] LIU W, VINTER B. CSR5: an efficient storage format for cross-platform sparse matrix-vector multiplication[C]// Proceedings of the 29th ACM International Conference on Supercomputing. New York: ACM, 2015: 339-350. [18] ECKER J P, BERRENDORF R, MANNUSS F. New efficient general sparse matrix formats for parallel SpMV operations [C]// Proceedings of the 2017 European Conference on Parallel Processing, LNCS 10417. Cham: Springer, 2017: 523-537. [19] XIE B, ZHAN J, LIU X, et al. CVR: efficient vectorization of SpMV on x86 processors[C]// Proceedings of the 2018 International Symposium on Code Generation and Optimization. New York: ACM, 2018: 149-162. [20] 程凯,田瑾,马瑞琳.基于GPU的高效稀疏矩阵存储格式研究[J].计算机工程, 2018, 44(8): 54-60.(CHENG K, TIAN J, MA R L. Study on efficient storage format of sparse matrix based on GPU[J]. Computer Engineering, 2018, 44(8): 54-60.) [21] ZHANG Y, YANG W, LI K, et al. Performance analysis and optimization for SpMV based on aligned storage formats on an ARM processor[J]. Journal of Parallel and Distributed Computing, 2021, 158: 126-137. [22] CORONADO-BARRIENTOS E, ANTONIOLETTI M, GARCIA-LOUREIRO A. A new AXT format for an efficient SpMV product using AVX-512 instructions and CUDA[J]. Advances in Engineering Software, 2021, 156: No.102997. [23] BIAN H, HUANG J, DONG R, et al. A simple and efficient storage format for SIMD-accelerated SpMV[J]. Cluster Computing, 2021, 24(4): 3431-3448. [24] KARIMI E, AGOSTINI N B, DONG S, et al. VCSR: an efficient GPU memory-aware sparse format[J]. IEEE Transactions on Parallel and Distributed Systems, 2022, 33(12):3977-3989. [25] VUDUC R W, MOON H J. Fast sparse matrix-vector multiplication by exploiting variable block structure[C]// Proceedings of the 2005 International Conference on High Performance Computing and Communications, LNCS 3726. Berlin: Springer, 2005: 807-816. [26] ALMASRI M, ABU-SUFAH W. CCF: an efficient SpMV storage format for AVX512 platforms[J]. Parallel Computing, 2020, 100: No.102710. [27] 杨世伟,蒋国平,宋玉蓉,等. 基于GPU的稀疏矩阵存储格式优化研究[J]. 计算机工程, 2019, 45(9): 23-31,39.(YANG S W, JIANG G P, SONG Y R, et al. Research on storage format optimization of sparse matrix based on GPU[J]. Computer Engineering, 2019, 45(9): 23-31, 39.) [28] LI Y, XIE P, CHEN X, et al. VBSF: a new storage format for SIMD sparse matrix-vector multiplication on modern processors[J]. The Journal of Supercomputing, 2020, 76(3): 2063-2081. [29] AHRENS P, BOMAN E G. On optimal partitioning for sparse matrices in variable block row format[EB/OL]. (2021-05-25)[2023-02-25].https://arxiv.org/pdf/2005.12414.pdf. [30] ALIAGA J I, ANZT H, GRÜTZMACHER T, et al. Compression and load balancing for efficient sparse matrix-vector product on multicore processors and graphics processing units[J]. Concurrency and Computation: Practice and Experience, 2022, 34(14): No.e6515. [31] NVIDIA. cuSPARSE library [EB/OL]. (2022-12)[2023-02-28].https://docs.nvidia.com/cuda/pdf/CUSPARSE_Library.pdf. [32] CHEN C, WU W. A geometric approach for analyzing parametric biological systems by exploiting block triangular structure[J]. SIAM Journal on Applied Dynamical Systems, 2022, 21(2): 1573-1596. [33] WU Z, PAN S, CHEN F, et al. A comprehensive survey on graph neural networks [J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4-24. [34] LIU F, XUE S, WU J, et al. Deep learning for community detection: progress, challenges and opportunities[C]// Proceedings of the 29th International Joint Conference on Artificial Intelligence. California: ijcai.org, 2020: 4981-4987. [35] RANI S, MEHROTRA M. Community detection in social networks: literature review[J]. Journal of Information and Knowledge Management, 2019, 18(2): No.1950019. [36] GALLOPOULOS E, PHILIPPE B, SAMEH A H. Banded linear systems[M]// Parallelism in Matrix Computations, SCIENTCOMP. Dordrecht: Springer, 2016: 91-163. [37] 中国科学院重庆绿色智能技术研究院. 一种带状稀疏矩阵的数据存储格式及其乘法加速方法: 202210931011.6[P]. 2022-11-08.(Chongqing Institute of Green and Intelligent Technology of Chinese Academy of Sciences. A data storage format for strip sparse matrix and its multiplication acceleration method: 202210931011.6 [P]. 2022-11-08.) [38] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks [EB/OL]. (2017-02-22)[2023-03-01].https://arxiv.org/pdf/1609.02907.pdf. [39] NVIIDA. Introduction of cuBLAS library[EB/OL]. [2023-04-01].http://docs.nvidia.com/cuda/cublas/index.html. [40] YAMAGUCHI T, BUSATO F. Accelerating matrix multiplication with block sparse format and NVIDIA tensor cores[EB/OL]. (2021-03-19)[2023-04-09].https://developer.nvidia.com/blog/accelerating- matrix- multiplication- with- block-sparse-format-and-nvidia-tensor-cores. [41] MORRIS C, KRIEGE N M,BAUSE F, et al. TUDataset: a collection of benchmark datasets for learning with graphs[EB/OL]. (2020-07-16)[2023-02-28].https://arxiv.org/pdf/2007.08663.pdf. [42] ZHANG M, CHEN Y. Link prediction based on graph neural networks [C]// Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2018: 5171-5181. [43] LESKOVEC J, KLEINBERG J, FALOUTSOS C. Graph evolution: densification and shrinking diameters[J]. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1): No.2. Band sparse matrix multiplication and efficient GPU implementation LIU Li1,2, CHEN Changbo1* (1,,400714,;2,,400714,) Sparse-dense Matrix Multiplication (SpMM) is widely used in the fields such as scientific computing and deep learning, and it is of great importance to improve its efficiency. For a class of sparse matrices with band feature, a new storage format BRCV (Banded Row Column Value) and an SpMM algorithm based on this format as well as an efficient Graphics Processing Unit (GPU) implementation were proposed. Due to the fact that each sparse band can contain multiple sparse blocks, the proposed format can be seen as a generalization of the block sparse matrix format. Compared with the commonly used CSR (Compressed Sparse Row)format, BRCV format was able to significantly reduce the storage complexity by avoiding redundant storage of column indices in sparse bands. At the same time, the GPU implementation of SpMM based on BRCV format was able to make more efficient use of GPU’s shared memory and improve the computational efficiency of SpMM algorithm by reusing the rows of both sparse and dense matrices. For randomly generated band sparse matrices, experimental results on two different GPU platforms show that BRCV outperforms not only cuBLAS (CUDA Basic Linear Algebra Subroutines), but also cuSPARSE based on CSR and block sparse formats. Specifically, compared with cuSPARSE based on CSR format, BRCV has the maximum speedup ratio of 6.20 and 4.77 respectively. Moreover, the new implementation was applied to accelerate the SpMM operator in Graph Neural Network (GNN). Experimental results on real application datasets show that BRCV outperforms cuBLAS and cuSPARSE based on CSR format, also outperforms cuSPARSE based on block sparse format in most cases. In specific, compared with cuSPARSE based on CSR format, BRCV has the maximum speedup ratio reached 4.47. The above results indicate that BRCV can improve the efficiency of SpMM effectively. band sparse matrix; sparse matrix storage format; sparse matrix multiplication; Graphics Processing Unit (GPU); shared memory This work is partially supported by Youth Top-notch Talent Project of Chongqing Talent Plan (2021000263). LIU Li, born in 1998, M. S. candidate. Her research interests include high-performance computing, deep learning. CHEN Changbo, born in 1981, Ph. D., research fellow. His research interests include computer algebra, high-performance computing, applied machine learning. TP332 A 1001-9081(2023)12-3856-12 10.11772/j.issn.1001-9081.2022111720 2022⁃11⁃21; 2023⁃05⁃04; 2023⁃05⁃06。 重庆英才计划青年拔尖人才项目(2021000263)。 刘丽(1998—),女,河南信阳人,硕士研究生,CCF会员,主要研究方向:高性能计算、深度学习;陈长波(1981—),男,山东济宁人,研究员,博士,CCF会员,主要研究方向:计算机代数、高性能计算、应用机器学习。3.3 等高的简化处理
4 实验与结果分析
4.1 基准
4.2 实验平台
4.3 测试用例
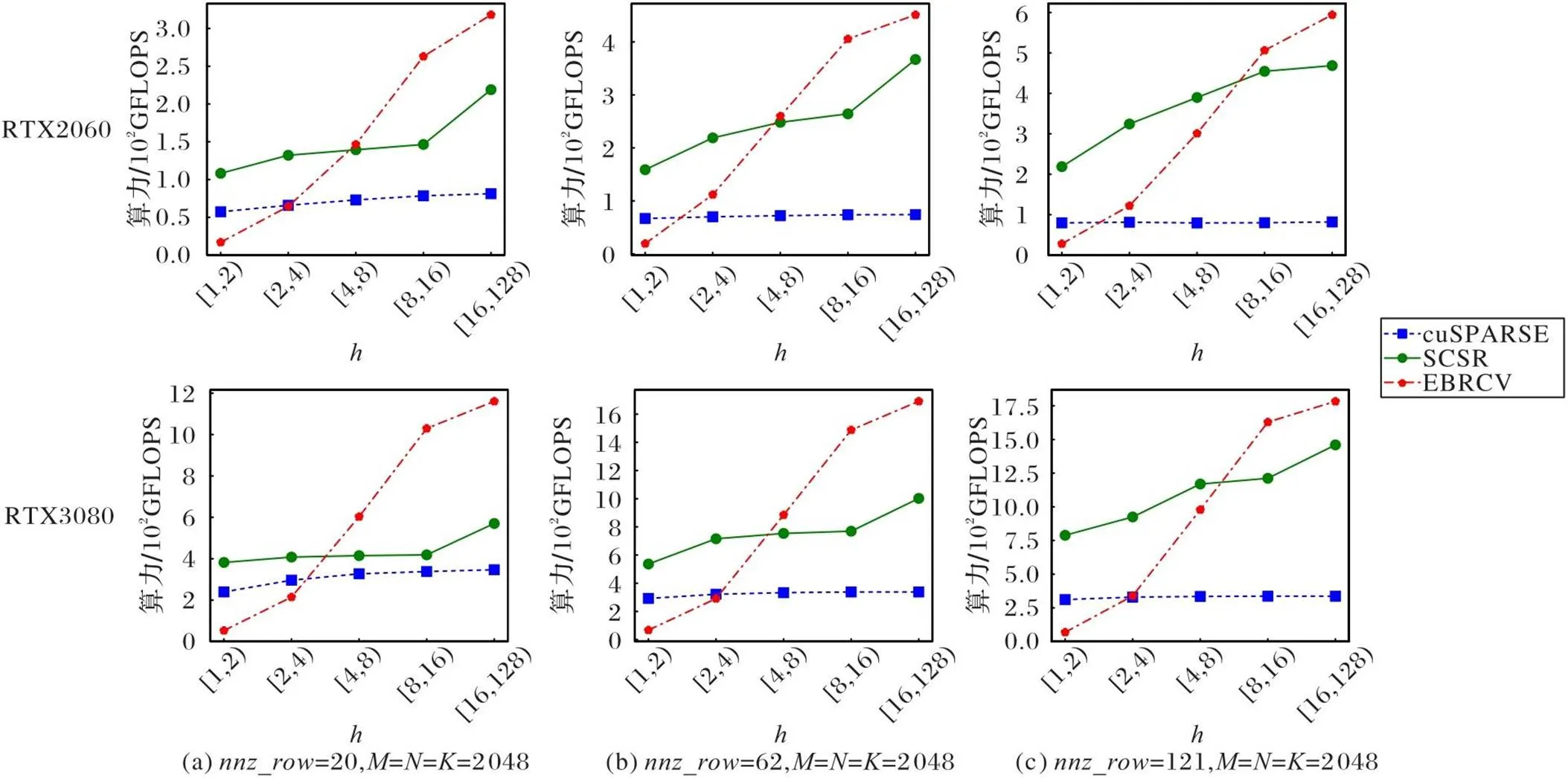
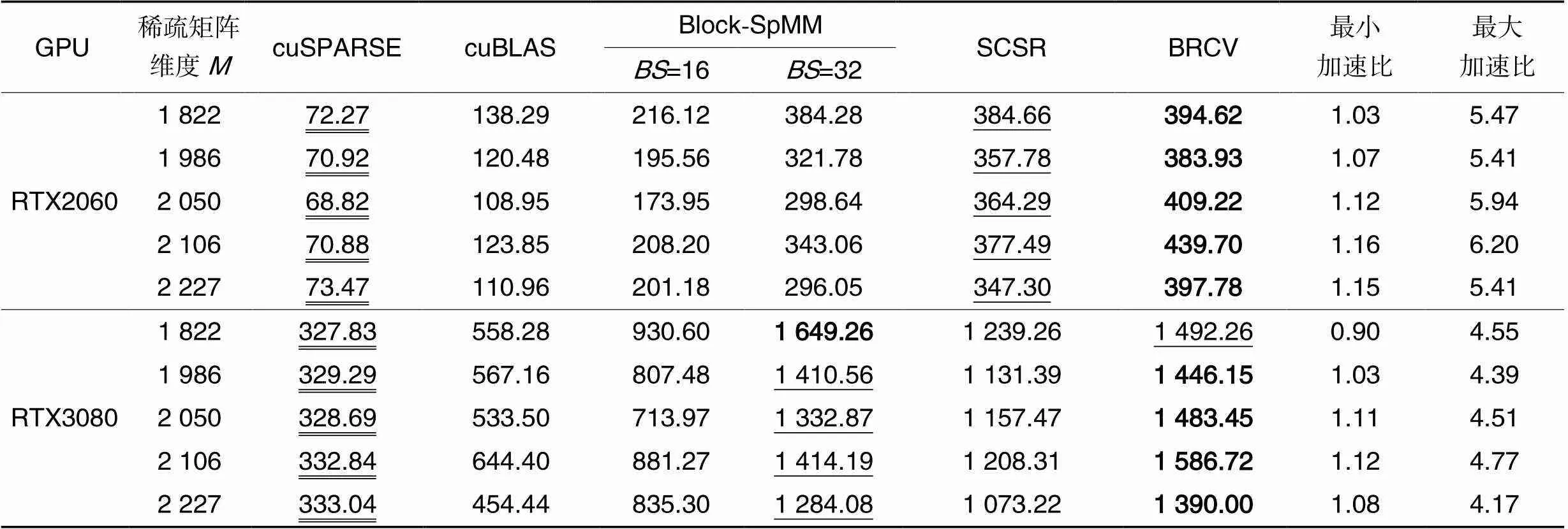
4.4 实验结果分析
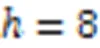
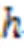
5 结语