卷积神经网络中基于差分隐私的动量梯度下降算法

张宇，蔡英，崔剑阳，张猛，范艳芳

卷积神经网络中基于差分隐私的动量梯度下降算法

张宇，蔡英*，崔剑阳，张猛，范艳芳

（北京信息科技大学 计算机学院，北京 100101）（∗通信作者电子邮箱ycai@bistu.edu.cn）

针对卷积神经网络（CNN）模型的训练过程中，模型参数记忆数据部分特征导致的隐私泄露问题，提出一种CNN中基于差分隐私的动量梯度下降算法（DPGDM）。首先，在模型优化的反向传播过程中对梯度添加满足差分隐私的高斯噪声，并用加噪后的梯度值参与模型参数的更新过程，从而实现对模型整体的差分隐私保护；其次，为了减少引入差分隐私噪声对模型收敛速度的影响，设计学习率衰减策略，改进动量梯度下降算法；最后，为了降低噪声对模型准确率的影响，在模型优化过程中动态地调整噪声尺度的值，从而改变在每一轮迭代中需要对梯度加入的噪声量。实验结果表明，与DP-SGD （Differentially Private Stochastic Gradient Descent）相比，所提算法可以在隐私预算为0.3和0.5时，模型准确率分别提高约5和4个百分点。可见，所提算法提高了模型的可用性，并实现了对模型的隐私保护。

卷积神经网络；差分隐私；动量梯度下降算法；深度学习；隐私保护

0 引言

卷积神经网络（Convolutional Neural Network， CNN）［1］凭借自动提取特征、局部权值共享和准确率较高的优点受到了广泛关注和研究，成功应用在图像分类［2］、特征提取［3］和图像检索［4］等多个领域，为挖掘一些复杂数据的信息提供了解决方法。大量的数据被收集为数据集训练CNN模型，然而这些数据中可能包含用户的一些敏感信息，例如在肿瘤识别的医学图像中含有患者的隐私信息，若这些隐私信息在训练模型的过程中被模型学习记忆，编码为模型的参数，会导致隐私存在泄露的风险。目前已有研究表明，攻击者可以通过窃取模型参数的手段，根据参数还原部分原始数据的特征，进一步推断训练数据集中的一些敏感信息［5］。

针对上述存在的隐私泄露问题，已有的解决方法可以分为数据加密、数据匿名和数据扰动这3种：数据加密主要通过同态加密［6］、安全多方计算［7］等加密算法保护原始数据，但是加密算法涉及大量运算，针对复杂问题的开销较大，实际中难以部署；数据匿名常用的方法是-匿名算法［8］以及一些拓展模型，需要假设攻击者的背景知识，这也使得数据匿名无法抵御不断变化的攻击方式，需要随着攻击方式的改变而更新；数据扰动主要应用差分隐私［9］实现对数据的保护，与数据加密和数据匿名相比，差分隐私拥有严格的数学证明过程，可以量化隐私保护水平，从而通过比较选取最优的解决方法，此外差分隐私开销较小，同时假设攻击者拥有尽可能多的背景知识，可以抵御背景知识攻击［10-12］。因此，本文采用差分隐私技术提供CNN模型训练过程中的隐私保护。

然而，将差分隐私技术应用于CNN模型时，由于在模型训练过程中引入了噪声，较大影响了模型的可用性，因此平衡隐私保护和模型可用性一直是该领域的一个重点研究问题。为了在使用优化算法优化模型的过程中实现差分隐私保护，同时降低噪声对模型收敛和模型准确率的影响，提高模型的可用性，本文提出了一种CNN中基于差分隐私的动量梯度下降算法（Gradient Descent with Momentum algorithm based on Differential Privacy in CNN， DPGDM）。

本文的主要工作内容有：

1）设计学习率衰减策略结合动量梯度下降算法优化模型。利用指数加权平均计算参数更新所需的梯度值，保留更多的梯度信息，降低噪声对模型收敛的影响，使模型能够在减少震荡的同时沿着正确的方向快速收敛。

2）在模型优化过程中，动态调整噪声尺度的值控制对梯度加入噪声量的大小，解决模型最终震荡无法收敛和准确率较低的问题，为模型提供隐私保护的同时提高模型的可用性。

3）在真实数据集上进行了大量对比实验，从准确率、隐私损失和参数设置等多方面进行了分析，充分验证了本文算法能够提高模型的可用性。

1 相关工作

深度学习领域中的隐私保护概念由Shokri等［13］首次引入，Shokri等［13］设计了一个系统使得多个参与者能够针对相同的目标共同训练神经网络模型，且无须共享自己使用的全部训练数据集，从而保护本地训练数据集中的隐私信息。Abadi等［14］改进了Shokri等［13］的方案，首次将差分隐私应用于深度学习模型的训练过程中并提出了DP-SGD（Differentially Private Stochastic Gradient Descent）算法。此后许多学者基于DP-SGD算法，研究如何应用差分隐私技术为深度学习模型提供隐私保护。

Yuan等［15］针对协作深度学习中共享本地CNN模型的参数导致的隐私泄露问题，提出对需要共享的参数上添加高斯噪声的方法提供隐私保护；但是对所有共享参数添加的都是相同大小的高斯噪声，对模型的准确率会产生较大的影响。Arachchige等［16］利用本地差分隐私技术，在CNN的结构中引入一个随机层，通过随机响应机制实现数据输入阶段的差分隐私保护。Gong等［17］根据模型输出和不同特征之间的相关性对梯度加入不同大小的拉普拉斯噪声；虽然对梯度加入拉普拉斯噪声能够满足-差分隐私，可以提供更高的隐私保护水平，但是-差分隐私的定义要求非常严格，实际中难以满足。在深度学习模型中，为了保持模型的可用性和高性能更常采用松弛差分隐私定义。Yu等［18］分析了训练过程中每批次样本数据的选取方式对DP-SGD算法中隐私损失的影响，将集中式差分隐私（Concentrated Differential Privacy， CDP）引入对DP-SGD算法的隐私损失度量中，更好地计算模型累积隐私损失。Ziller等［19］为了以高效的内存和并行的方式实现DP-SGD算法，设计了一个差分隐私深度学习框架，同时使得DP-SGD算法可以兼容多种神经网络。Papernot等［20］针对DP-SGD算法在优化模型过程中可能存在梯度爆炸导致丢失过多梯度信息的问题，从激活函数的角度分析并提出了一种新的激活函数，保证在应用DP-SGD算法提供隐私保护的同时模型具有较高的准确率。

综上，目前大部分应用于CNN模型中的差分隐私保护算法仍然基于DP-SGD算法，平衡模型的可用性和隐私保护水平依旧是一个关键性问题。模型的收敛和准确率与选择的模型优化算法以及对模型加入的噪声量有关，而目前与差分隐私技术结合的优化算法常选择随机梯度下降算法，但随机梯度下降算法本身存在较大的局限性，在模型收敛过程中仍然存在着较大的震荡，并且加入噪声后会更影响梯度的下降方向。针对该问题，李敏等［21］和余方超等［22］提出将Adam（Adaptive moment estimation）优化算法与差分隐私理论相结合，利用Adam优化算法自适应的优点加快模型收敛，促使模型获得一个较高的准确率。但是Adam算法中的二阶动量并不是单调变化的，在模型训练后期可能会导致学习率的震荡，致使最终无法收敛，并且有研究发现Adam优化算法虽然可以加快模型收敛但是最终的收敛效果较差。

针对以上将差分隐私应用于CNN模型存在的不足，本文提出基于差分隐私的动量梯度下降算法。通过在优化模型的过程中改变噪声尺度的值，对梯度加入不同大小的高斯噪声，用加噪后的梯度进行参数更新为模型整体提供隐私保护，同时保证模型拥有一个较高的准确率。此外，动量梯度下降算法相较于随机梯度下降算法，引入了“惯性”的概念，可以抑制随机梯度下降算法的震荡，结合学习率衰减策略可以降低噪声对模型收敛的影响，也解决了直接用Adam自适应学习率优化算法出现后期难以调整前期过拟合效果的问题。

2 预备知识

2.1　差分隐私

差分隐私有详细完整的数学证明过程，可以通过数学表达式对隐私保护水平进行量化表示，主要实现机制是对原始数据加入满足特定分布的噪声，且此后修改任何一条数据都不会对整体数据的统计结果产生较大的影响，从而实现对数据的隐私保护，相关定义如下。

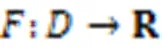
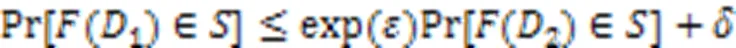
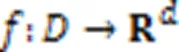
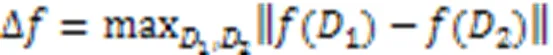
局部敏感度的定义和全局敏感度的定义是相似的，全局敏感度是局部敏感度的最大值，同时会影响加入噪声的大小。

定义3 高斯机制［18］。对任意一个函数加入满足（，）-差分隐私的高斯噪声，如式（3）所示：

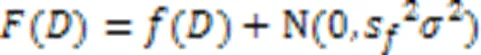
2.2　CNN

CNN的结构可以按照传统的分层结构分为3层：输入层、隐藏层和输出层［23］。

输入层 在应用CNN时一般会对输入数据进行归一化，以提升模型的学习效率使它拥有更好的表现。

隐藏层 CNN的隐藏层是核心部分，分为卷积层、池化层和全连接层这3部分：卷积层通过许多个卷积核对输入的数据进行特征提取，自动提取特征降低了其他神经网络需要人工提取特征的工作量，同时还具有权值共享的特点；池化层可以通过选取池化函数对卷积层输出的特征图进行进一步的特征选择，保留更加重要的信息，能够再次降低计算量；全连接层通过选用的激活函数对提取后的特征进行非线性组合，以获得最后的输出结果［24-25］。

输出层 与传统的神经网络的输出层相同，输出CNN模型的最终结果。

2.3　动量梯度下降算法

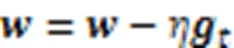
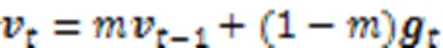
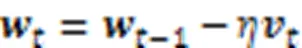
3 优化策略与算法

CNN模型对参数的变化非常敏感，如果在训练好的模型参数上加入差分隐私噪声会使得整个模型失去可用性；因此，需要在训练的过程中对模型采用差分隐私机制。本文结合优化算法和差分隐私，通过在模型训练过程中对梯度加入满足差分隐私的高斯噪声，用加噪后的梯度参与后续参数更新，间接实现对整个模型训练过程的扰动。此外，为了降低噪声对模型收敛和模型准确率的影响，提高模型的可用性，本文采用动量梯度下降算法优化模型，加强梯度之间的关联，保留更多的梯度信息；同时设计学习率衰减策略和噪声尺度动态调整策略，保证模型能够减少震荡并沿着正确方向快速收敛。

3.1　学习率衰减策略

动量梯度下降算法在整个模型参数优化过程中采用固定大小的学习率，学习率表示参数更新时移动的步长，过大或过小都会导致模型无法正常收敛或者收敛缓慢，因此本文考虑在应用动量梯度下降算法的同时不断调整学习率的大小。

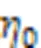
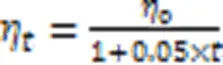
其中表示当前训练处于的轮次数。

3.2　噪声尺度动态调整策略

差分隐私最初的定义要求过于严格，本文采用差分隐私的松弛定义（，）-差分隐私，为了满足该差分隐私定义通常选择高斯噪声机制。目前对参数梯度加入的噪声量通常在整个训练阶段都保持不变，但是加入固定大小的噪声对模型的训练会产生较大的影响，因为在模型训练后期，较大的噪声会导致损失函数存在较多震荡状态而无法尽快收敛，最终获得的模型预测准确率也偏低。

根据定义3可知，噪声尺度实际决定每一次对梯度平均值加入噪声的大小。因此，本文考虑随着模型训练轮次数的增加，逐渐减小噪声尺度，则可以在后期加入较小的噪声；但是为了提供隐私保护不能无限减小，因此需要设置一个最小值对噪声尺度进行限制，具体实现过程如算法1所示。

算法1 动态调整噪声尺度算法。

输入 噪声尺度初始值0，最小值min，CNN模型的训练轮次数的值；

输出 当前训练阶段的σ。

4） else

6） returnσ

3.3　差分隐私动量梯度下降算法描述

CNN模型的训练主要是在反向传播过程中，通过优化算法不断更新模型参数，从而使模型收敛。目前模型的训练主要采用基于梯度下降的优化算法最小化给定的损失函数，如果在梯度上加入噪声，相当于间接对参数的更新过程进行了扰动，可以为模型整体提供隐私保护。

基于以上两个优化策略和动量梯度下降算法，本文提出了DPGDM，具体实现如算法2所示。首先通过噪声尺度动态调整策略计算该轮训练需要加入的噪声量，在训练前后期对梯度加入不同大小的噪声，解决因加入固定大小噪声导致模型在快收敛时一直震荡而无法收敛的问题；其次采用动量梯度下降算法优化模型参数，同时结合学习率衰减策略，应用指数加权平均估计每一次的梯度值，保留了更多的梯度信息，提高模型的准确率和收敛速度。

算法2主要分为五部分。

第一部分首先初始化参数，其次在每开始一轮新的训练时，动态更新学习率和噪声尺度的大小，在一轮训练中的每次迭代中，学习率和噪声尺度的大小都不会改变，如算法2中1）～ 4）所示。

第二部分需要从训练数据集中随机获得批量样本数据，根据给定的损失函数计算每一个样本数据，求解对应的梯度值，如算法2中的5）～6）所示。

第三部分对求出的每一个样本数据的梯度值进行裁剪，如果梯度值的二范数超出设定的阈值，梯度值的大小将被更新为阈值；如果在阈值范围内，梯度值保留原有结果，如算法2中7）所示。

第四部分是根据当前噪声尺度的值，对裁剪后的梯度加入满足差分隐私定义的高斯噪声，加入噪声后的梯度平均值参与之后的参数更新过程，从而为模型整体提供隐私保护，如算法2中8）所示。

第五部分是依据动量梯度下降算法的执行过程，利用噪声梯度平均值计算当前梯度值对应的动量值，根据当前动量更新参数，如算法2中9）～11）所示。

算法2 DPGDM算法。

2） for epoch in range （1，）：

//表示epoch当前的值，为模型训练的轮次总数

5） 随机获取批处理数据D，其中包含样本数为

3.4　隐私性分析

DPGDM算法中针对每一次迭代过程中的梯度值都加入了满足（，）-差分隐私定义的高斯噪声，由于差分隐私具有后处理免疫［9］的性质，后续根据加噪后的梯度值计算动量也不会影响满足差分隐私。

将差分隐私应用于CNN，由于对梯度值加入噪声使得在模型训练过程中的每一次迭代都会产生一部分隐私损失，因此需要在训练过程中一直追踪DPGDM算法产生的隐私损失的累积结果。其中，隐私损失并不是一个具体的数值，而是一个随机变量，具体的含义如定义4所示。

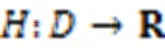
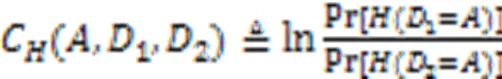
Abadi等［14］提出的矩会计方法可以计算模型整体的累计隐私损失，矩会计方法的思想就是将总的隐私损失看成每一次迭代产生的隐私损失的加和分布，该方法的计算最终可以和Rényi差分隐私［26-28］进行直接联系，并且Rényi差分隐私在计算隐私损失时具有更强的优越性，因此本文将结合它计算在训练过程中DPGDM算法产生的累积隐私损失，利用Rényi差分隐私确定矩会计方法中的阶的值。

根据矩会计方法，假设采用DPGDM算法优化CNN模型的训练机制表示为，时刻在相邻数据库1和2上模型的隐私损失可以表示如下：

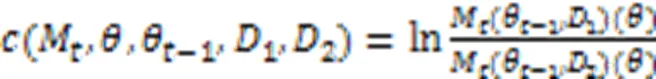
假设模型训练轮次为，由于每一轮的训练都是独立的，根据差分隐私的组合定理［9］可知模型整体的隐私损失变量可以表示为每一时刻隐私损失变量的求和，如式（9）所示：

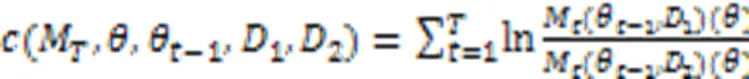
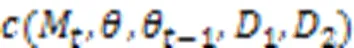
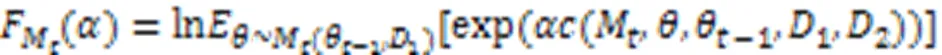
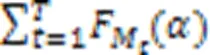
4 实验与结果分析

4.1　数据集和实验设置

本文实验过程中用到的数据集为MNIST［14］、Fashion-MNIST［29］和CIFAR-10［14］这3个公开的真实数据集。MNIST数据集由美国国家标准与技术研究所收集，包含了250个不同的人对数字0～9的手写体灰度图像，其中图像大小为28×28，分为6万张训练数据，1万张测试数据。Fashion-MNIST数据集由德国一家时尚公司提供的包含10个类别的灰色衣服图像组成，共有7万张图片，分为6万张训练数据，1万张测试数据。CIFAR-10是一个彩色图像数据集，分为10个类别的物体，其中图像大小为32×32，包含了5万张训练数据，1万张测试数据。

实验采用的CNN结构根据数据集的不同有所变动。针对MNIST数据集和Fashion-MNIST数据集，网络的输入为28×28的原始灰度图像，之后经过第1个卷积层，该层使用16个8×8的卷积核，再连接一个池化层，采用的池化函数为求最大值的函数，卷积核大小为2×2；然后连接第2个卷积层，该层使用32个4×4的卷积核，每1个卷积层之后都连接1个池化层，便于对卷积层提取的特征进行再次选择，因此第2个卷积层之后也连接了1个卷积核为2×2的最大池化层。接着有2个全连接层，网络中使用的激活函数为ReLU（Rectified Linear Unit）函数，最后通过softmax函数输出分类结果。针对CIFAR-10数据集，CNN的结构共有3个卷积层，每一个卷积层都使用5×5的卷积核，卷积层之后连接最大池化层，池化层采用2×2的卷积核。之后的网络结构分为扁平层和2个全连接层这3个部分，网络中采用的激活函数仍为ReLU函数，分类结果应用softmax函数输出。

实验中在3个数据集上所采用的参数设置如表1所示。

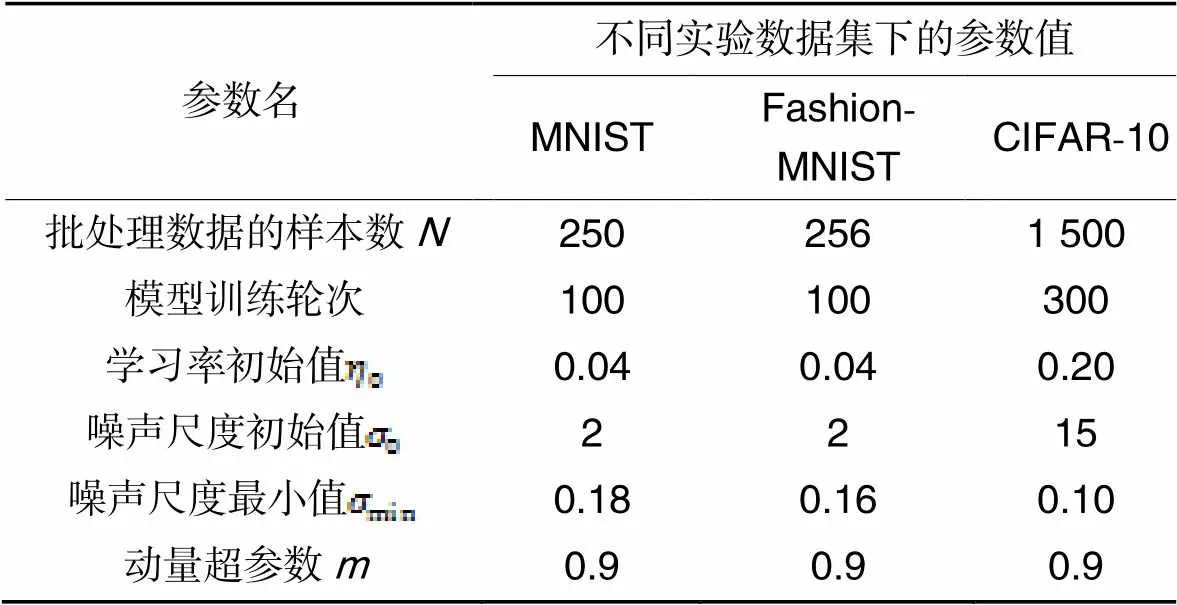
表1　实验参数

4.2　实验结果分析

在实验中将DPGDM在多个数据集上进行了多组实验，并与其他多种算法进行对比，通过观察模型的预测准确率和隐私保护水平评估算法的优劣，此外还设置不同大小的参数，观察参数取值对模型产生的影响。

4.2.1MNIST数据集

在MNIST数据集上将DPGDM与DP-SGD算法［14］、DP-Adam算法［21］和DPADAM（ADAptive Moment estimation with Differential Privacy）算法［22］进行对比，为了查看各算法在提供差分隐私保护时对模型准确率造成的损失情况，同时与在没有隐私保护下训练模型（NO-PRIVACY）的准确率进行了对比，如图1所示。

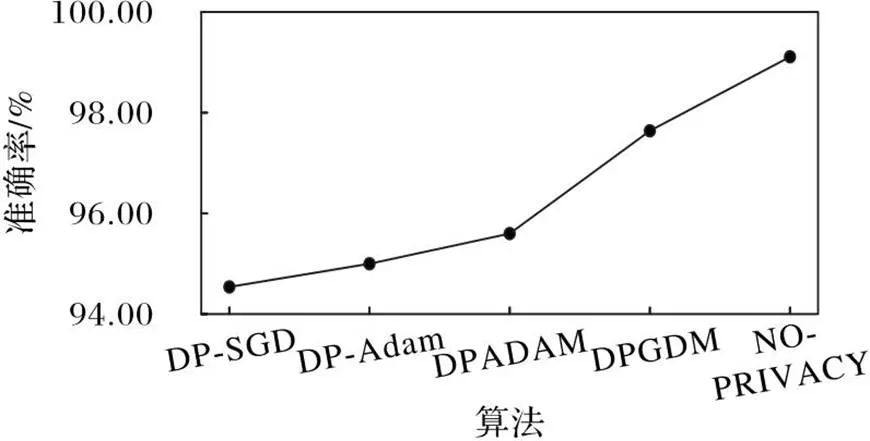
图1　不同算法在MNIST数据集上的准确率对比

由图1可知，DPGDM算法训练模型的效果优于其他对比算法，经过100轮训练后可以达到97.64%的准确率，比其他差分隐私保护算法的准确率高2～4个百分点。在没有隐私保护情况下训练模型的准确率可以达到99.11%，相较于有隐私保护的DPGDM算法、DP-SGD算法、DP-Adam算法［21］和DPADAM算法［22］准确率分别降低了1.47%、4.57%、4.11%和3.51%。实验结果表明，DPGDM可以在提供差分隐私保护的前提下保证模型仍然拥有一个较高的准确率。

图2给出了DPGDM、DP-SGD算法和DP-Adam算法在不同隐私预算值下，对MNIST数据集进行训练后的模型准确率。由图2可知，在不同的隐私预算值下，DPGDM的模型准确率始终处于一个较高水平。隐私预算的值越小说明可以提供的隐私保护水平越高。从图2中可以看到，当隐私预算较小时，例如取值为0.3，采用DPGDM的准确率高于采用DP-SGD算法约5个百分点，准确率能够达到89.32%；当取值为0.5时，采用DPGDM的准确率可以达到92.92%，相较于DP-SGD算法提高了约4个百分点。说明DPGDM在为模型整体提供更高隐私保护水平的前提下，能够保证模型仍然拥有较好的性能。

图3给出了DPGDM、DP-SGD算法和DPADAM算法在设置不同噪声尺度初始值时，针对MNIST数据集训练50轮次后的模型准确率。噪声尺度直接影响了在每一轮训练过程中对梯度加入高斯噪声的大小。从图3中可以看到，随着噪声尺度的增加，对模型引入的噪声量变多，所有算法的模型准确率整体呈下降趋势，但是采用DPGDM算法的模型准确率下降缓慢，且依旧可以维持一个较高的准确率。这是因为DPGDM算法随着模型的训练会衰减加入模型的噪声量，而其他两种算法在优化模型的过程中始终对梯度加入固定大小的噪声。

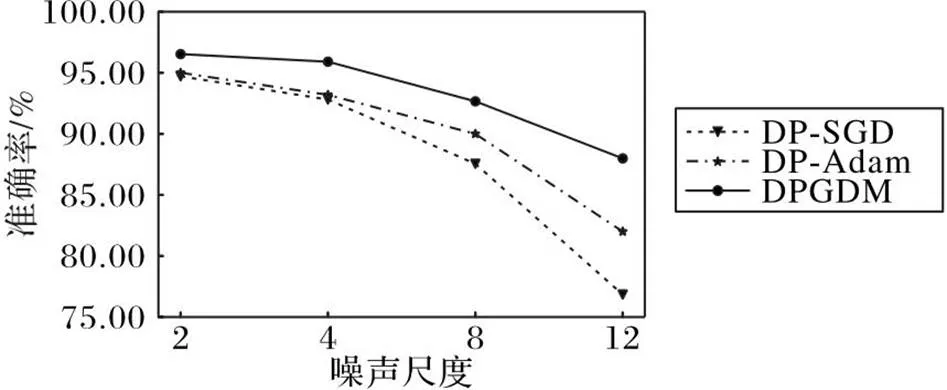
图3　不同噪声尺度下不同算法的模型准确率对比

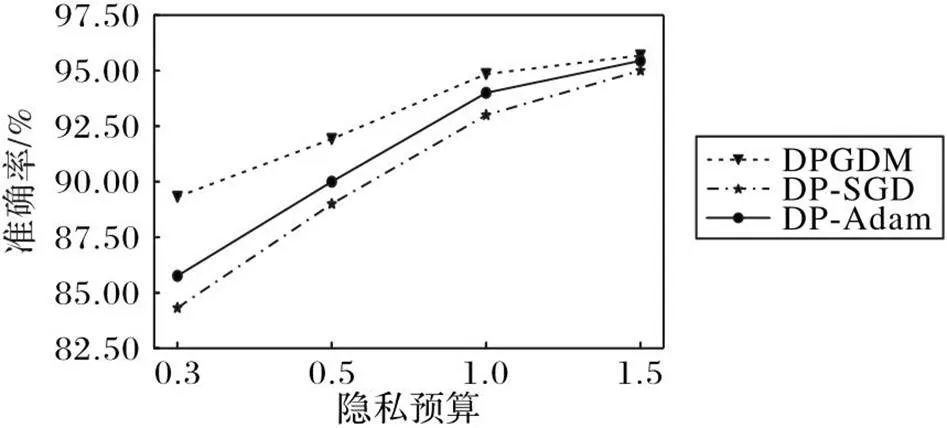
图2　不同隐私预算下不同算法在MNIST数据集上的准确率对比

学习率的取值对模型最终训练的效果会产生较大的影响，过大过小都会使得模型收敛较慢，不能在较少的训练轮次数中达到一个较高的准确率。图4给出了当设置不同大小的学习率初始值时，DPGDM算法在MNIST数据集上训练50轮次后的模型准确率，可以看到当学习率初始值为0.04时，模型的训练效果较好，因此在MNIST数据集上的实验过程中，学习率的初始值设置为0.04。

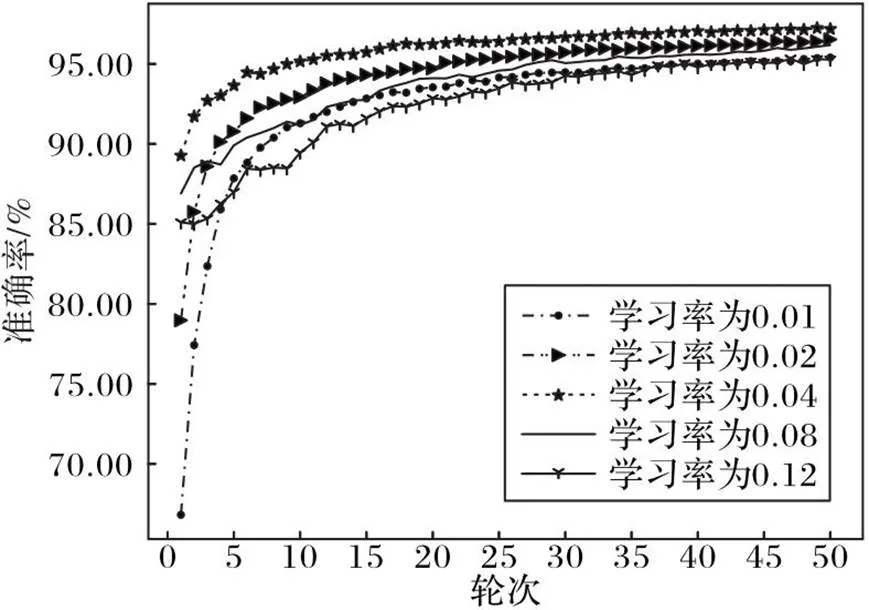
图4　不同学习率下的模型准确率对比

4.2.2Fashion-MNIST数据集

在Fashion-MNIST数据集上将DPGDM与DP-SGD算法和基于PSO的差分隐私算法（Differential Privacy algorithm based on PSO， DP-PSO）［29］进行对比，如表2所示。

由表2可知，DPGDM算法在准确率上优于对比算法，与未使用隐私保护的模型训练结果相比，损失的准确率也最低。实验结果进一步说明了本文提出的DPGDM算法可以更好地提升模型可用性。

表2不同算法在Fashion-MNIST数据集上的准确率对比 单位：%

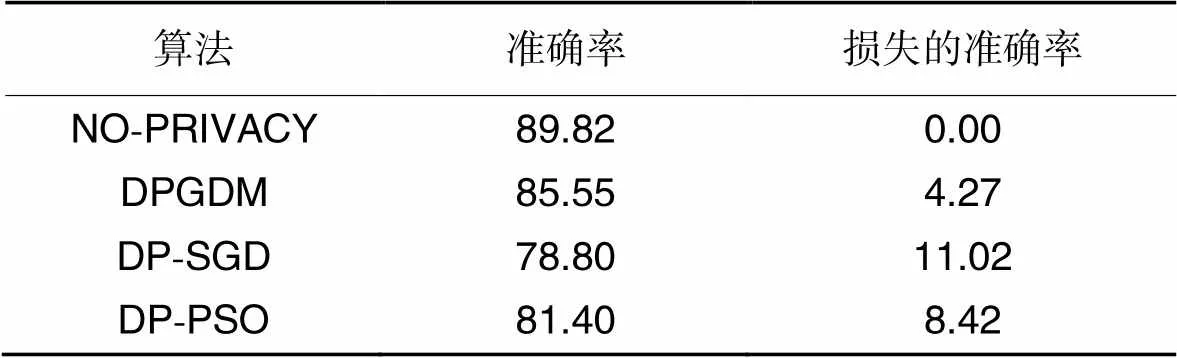
Tab.2　Accuracy comparison of different algorithms on Fashion-MNIST dataset unit：%

为了更好地验证本文算法的适用性，在不同的隐私预算下，给出了几种算法在Fashion-MNIST数据集上训练模型的准确率结果，如图5所示。

由图5可知，与其他算法相比，DPGDM在隐私预算取值为4、6、8、10时，都能够较好地收敛，并获得较高的模型准确率。在隐私预算设置为10时，DPGDM算法最终的收敛效果远领先于其他两种算法，比DP-SGD算法和DP-PSO算法的准确率分别高出了7个和2个百分点，并且随着隐私预算的降低，DPGDM的准确率受到的影响较小。

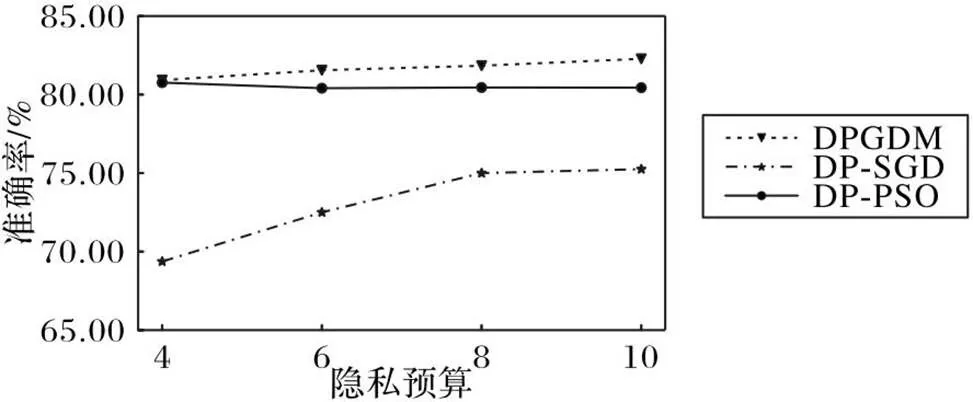
图5　不同隐私预算下不同算法在 Fashion-MNIST数据集上的模型准确率对比

4.2.3CIFAR-10数据集

为了进一步地验证DPGDM的普适性，在更为复杂的CIFAR-10数据集上将DPGDM算法与DP-SGD算法和文献［20］所提的改进激活函数提升模型性能的方法进行了对比，如表3所示。由表3可知，DPGDM算法损失的准确率与其他算法相比最低，说明DPGDM算法可以在提供差分隐私保护的前提下提高模型的可用性。

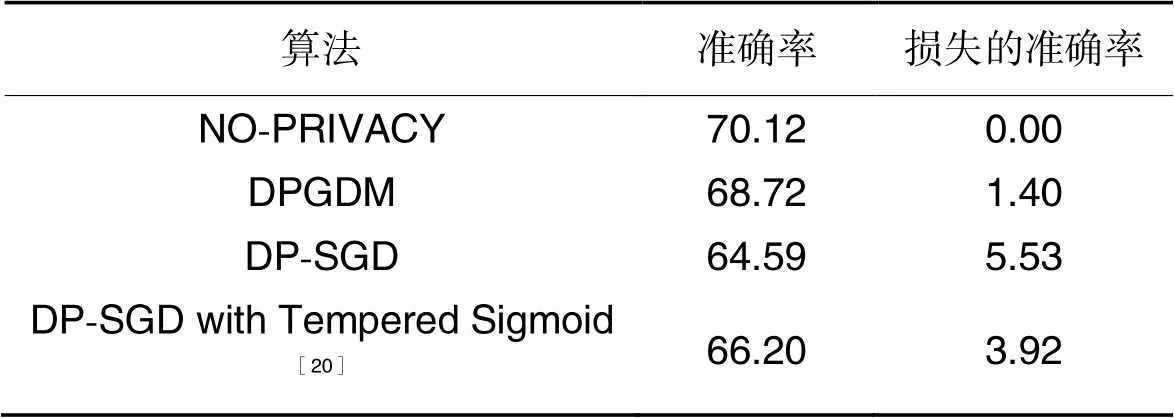
表3　不同算法在CIFAR-10数据集上的准确率对比 单位：%

在实验过程中发现，当一些超参数的初始值设置不合理时，DP-SGD算法的性能会受到较大的影响，而DPGDM算法受到的影响较小，依旧能够稳定收敛，如图6、7所示。

图6给出了当参数初始值设置不合理情况下，DPGDM算法和DP-SGD算法在CIFAR-10数据集上优化模型的准确率结果，图7给出了训练过程中损失函数的变化情况。DP-SGD算法在该参数设置下，由于初始设定的不合理的学习率和噪声尺度值在训练过程中一直保持不变，损失函数在训练中后期出现波动，模型最终无法正常收敛；而DPGDM算法在训练期间会不断调整学习率和噪声尺度的值，损失函数虽然出现小幅波动但整体呈下降趋势，最终在300轮训练后达到了69.90%的准确率。

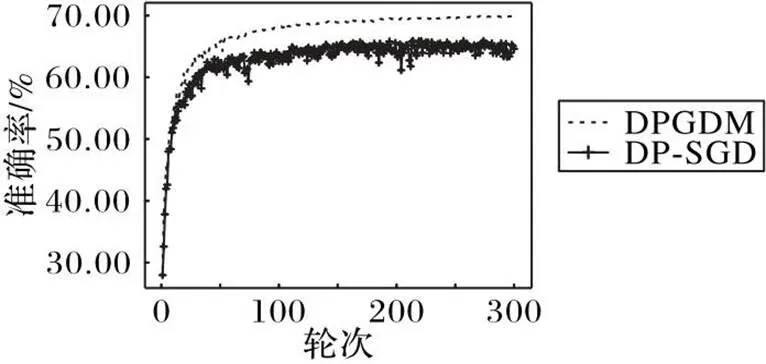
图6　CIFAR-10数据集上的模型准确率对比

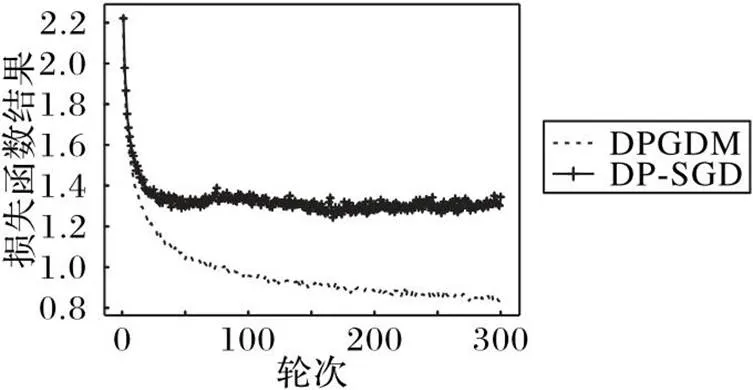
图7　CIFAR-10数据集上的损失函数变化情况

5 结语

本文提出了一种CNN中基于差分隐私的动量梯度下降算法（DPGDM）。用指数加权平均方法计算梯度，从而保留梯度更多的信息；同时在模型训练过程中动态调整学习率的大小，改变噪声尺度的值，使得在训练的前后期对梯度加入不同水平的高斯噪声，保证模型能够减少震荡的同时沿着正确的方向快速收敛，降低噪声对模型准确率的影响。实验结果表明DPGDM可以更好地平衡差分隐私保护和模型可用性之间的关系。由于梯度裁剪阈值的选择会影响梯度的裁剪过程和差分隐私中的灵敏度大小，未来会继续研究对梯度进行分类，对不同类别的梯度分组进行裁剪和加入噪声。

[1] ALZUBAIDI L， ZHANG J， HUMAIDI A J， et al. Review of deep learning： concepts， CNN architectures， challenges， applications， future directions［J］. Journal of Big Data， 2021， 8： Article No. 53.

[2] SUN Y， XUE B， ZHANG M， et al. Automatically designing CNN architectures using the genetic algorithm for image classification［J］. IEEE Transactions on Cybernetics， 2020， 50（9）： 3840-3854.

[3] 季长清，高志勇，秦静，等.基于卷积神经网络的图像分类算法综述［J］.计算机应用，2022，42（4）：1044-1049.（JI C Q， GAO Z Y， QIN J， et al. Review of image classification algorithms based on convolutional neural network［J］. Journal of Computer Applications， 2022，42（4）：1044-1049.）

[4] HUSAIN S S， BOBER M. REMAP： multi-layer entropy-guided pooling of dense CNN features for image retrieval［J］. IEEE Transactions on Image Processing， 2019， 28（10）： 5201-5213.

[5] FREDRIKSON M， JHA S， RISTENPART T. Model inversion attacks that exploit confidence information and basic countermeasures［C］// Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2015： 1322-1333.

[6] HERNANDEZ MARCANO N J， MOLLER M， HANSEN S， et al. On fully homomorphic encryption for privacy-preserving deep learning ［C］// Proceedings of the 2019 IEEE Globecom Workshops. Piscataway： IEEE， 2019： 1-6.

[7] TRAN A-T， LUONG T-D， KARNJANA J， et al. An efficient approach for privacy preserving decentralized deep learning models based on secure multi-party computation［J］. Neurocomputing， 2021， 422： 245-262.

[8] MEDEN B， EMERŠIČ Ž， ŠTRUC V， et al.-Same-Net：-anonymity with generative deep neural networks for face deidentification ［J］. Entropy， 2018， 20（1）： 60.

[9] DWORK C. Differential privacy［C］// Proceedings of the 33rd International Colloquium on Automata， Languages and Programming. Berlin： Springer， 2006： 1-12.

[10] CAI Y， ZHANG Y， QU J， et al. Differential privacy preserving dynamic data release scheme based on Jensen-Shannon divergence［J］. China Communications， 2022，19（6）：11-21.

[11] 屈晶晶，蔡英，范艳芳，等. 基于-prototype聚类的差分隐私混合数据发布算法［J］. 计算机科学与探索， 2021， 15（1）：109-118.（QU J J， CAI Y， FAN Y F， et al. Differentially private mixed data release algorithm based on-prototype clustering［J］. Journal of Frontiers of Computer Science and Technology， 2021，15（1）：109-118.）

[12] ZHANG Y， CAI Y， ZHANG M， et al. A survey on privacy-preserving deep learning with differential privacy ［C］// Proceedings of the 2021 International Conference on Big Data and Security. Singapore： Springer， 2022： 18-30.

[13] SHOKRI R， SHMATIKOV V. Privacy-preserving deep learning ［C］// Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2015： 1310-1321.

[14] ABADI M，CHU A， GOODFELLOW I， et al. Deep learning with differential privacy［C］// Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2016： 308-318.

[15] YUAN D， ZHU X， WEI M， et al. Collaborative deep learning for medical image analysis with differential privacy ［C］// Proceedings of the 2019 IEEE Global Communications Conference. Piscataway： IEEE， 2019： 1-6.

[16] ARACHCHIGE P C M， BERTOK P， KHALIL I， et al. Local differential privacy for deep learning ［J］. IEEE Internet of Things Journal， 2019， 7（7）： 5827-5842.

[17] GONG M， PAN K， XIE Y， et al. Preserving differential privacy in deep neural networks with relevance-based adaptive noise imposition［J］. Neural Networks， 2020， 125： 131-141.

[18] YU L， LIU L， PU C， et al. Differentially private model publishing for deep learning ［C］// Proceedings of the 2019 IEEE Symposium on Security and Privacy. Piscataway： IEEE， 2019： 332-349.

[19] ZILLER A， USYNIN D， BRAREN R， et al. Medical imaging deep learning with differential privacy［J］. Scientific Reports， 2021， 11： Article No. 13524.

[20] PAPERNOT N， THAKURTA A， SONG S， et al. Tempered sigmoid activations for deep learning with differential privacy［J］. Proceedings of the AAAI Conference on Artificial Intelligence， 2021， 35（10）： 9312-9321.

[21] 李敏，李红娇，陈杰.差分隐私保护下的Adam优化算法研究［J］.计算机应用与软件，2020，37（6）：253-258，296.（LI M， LI H J， CHEN J. Adam optimization algorithm based on differential privacy protection［J］. Computer Applications and Software， 2020，37（6）：253-258，296.）

[22] 余方超，方贤进，张又文，等.增强深度学习中的差分隐私防御机制［J］.南京大学学报（自然科学），2021，57（1）：10-20.（YU F C， FANG X J， ZHANG Y W， et al. Enhanced differential privacy defense mechanism in deep learning［J］. Journal of Nanjing University （Natural Science）， 2021，57（1）：10-20.）

[23] YAMASHITA R， NISHIO M， DO R K G， et al. Convolutional neural networks： an overview and application in radiology［J］. Insights into Imaging， 2018， 9（4）： 611-629.

[24] KATTENBORN T， LEITLOFF J， SCHIEFER F， et al. Review on Convolutional Neural Networks （CNN） in vegetation remote sensing［J］. ISPRS Journal of Photogrammetry and Remote Sensing， 2021， 173： 24-49.

[25] KIRANYAZ S， AVCI O， ABDELJABER O， et al. 1D convolutional neural networks and applications： a survey［J］. Mechanical Systems and Signal Processing， 2021， 151： 107398.

[26] MIRONOV I. Rényi differential privacy［C］// Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium. Piscataway： IEEE， 2017： 263-275.

[27] 谭作文，张连福.机器学习隐私保护研究综述［J］.软件学报，2020，31（7）：2127-2156.（TAN Z W， ZHANG L F. Survey on privacy preserving techniques for machine learning ［J］. Journal of Software， 2020，31（7）：2127-2156.）

[28] YOUSEFPOUR A， SHILOV I， SABLAYROLLES A， et al. Opacus： user-friendly differential privacy library in PyTorch ［EB/OL］. ［2022-08-22］.https：//arxiv.org/pdf/2109.12298.pdf.

[29] 张攀峰，吴丹华，董明刚. 基于粒子群优化的差分隐私深度学习模型［J］. 计算机工程， 2023，49（9）： 144-157.（ZHANG P F， WU D H， DONG M G. Differential privacy deep learning model based on particle swarm optimization ［J］. Computer Engineering， 2023，49（9）： 144-157.）

Gradient descent with momentum algorithm based on differential privacy in convolutional neural network

ZHANG Yu， CAI Ying*， CUI Jianyang， ZHANG Meng， FAN Yanfang

（，，100101，）

To address the privacy leakage problem caused by the model parameters memorizing some features of the data during the training process of the Convolutional Neural Network （CNN） models， a Gradient Descent with Momentum algorithm based on Differential Privacy in CNN （DPGDM） was proposed. Firstly， the Gaussian noise meeting differential privacy was added to the gradient in the backpropagation process of model optimization， and the noise-added gradient value was used to participate in the model parameter update process， so as to achieve differential privacy protection for the overall model. Secondly， to reduce the impact of the introduction of differential privacy noise on convergence speed of the model，a learning rate decay strategy was designed and then the gradient descent with momentum algorithm was improved. Finally， to reduce the influence of noise on the accuracy of the model， the value of the noise scale was adjusted dynamically during model optimization， thereby changing the amount of noise that needs to be added to the gradient in each round of iteration. Experimental results show that compared with DP-SGD （Differentially Private Stochastic Gradient Descent） algorithm， the proposed algorithm can improve the accuracy of the model by about 5 and 4 percentage points at privacy budget of 0.3 and 0.5， respectively， proving that by using the proposed algorithm， the model usability is improved and privacy protection of the model is achieved.

Convolutional Neural Network (CNN); differential privacy; gradient descent with momentum algorithm; deep learning; privacy protection

This work is partially supported by Natural Science Foundation of Beijing-Haidian Original Innovation Joint Fund （L192023）.

ZHANG Yu， born in 1997， M. S. candidate. Her research interests include deep learning， differential privacy.

CAI Ying， born in 1966， Ph. D， professor. Her research interests include internet of vehicles， edge computing， privacy protection， computer security.

CUI Jianyang， born in 1996， M. S. candidate. His research interests include vehicular ad hoc network， privacy protection.

ZHANG Meng，born in 1996， M. S. candidate. His research interests include image retrieval， privacy protection.

FAN Yanfang， born in 1979， Ph. D， associate professor. Her research interests include information security， internet of vehicles， edge computing.

TP309

A

1001-9081（2023）12-3647-07

10.11772/j.issn.1001-9081.2022121881

2022⁃12⁃26；

2023⁃03⁃19；

2023⁃03⁃24。

北京市自然科学基金-海淀原始创新联合基金资助项目（L192023）。

张宇（1997—），女，河北石家庄人，硕士研究生，主要研究方向：深度学习、差分隐私；蔡英（1966—），女，四川绵阳人，教授，博士，CCF会员，主要研究方向：车联网、边缘计算、隐私保护、计算机安全；崔剑阳（1996—），男（满族），河北承德人，硕士研究生，主要研究方向：车载自组织网络、隐私保护；张猛（1996—），男，河北定州人，硕士研究生，主要研究方向：图像检索、隐私保护；范艳芳（1979—），女，山西运城人，副教授，博士，主要研究方向：信息安全、车联网、边缘计算。